一道圆锥曲线的解析

◇ 福建 苏灿强



一道圆锥曲线的解析

◇ 福建 苏灿强

直线与圆锥曲线的位置关系是历年高考的必考内容,是高考的热点和难点,解答题一般设置在压轴题上,主要考查学生的综合能力、思维拓展及运算能力,囊括高中重要的数学思想和方法,可以准确地衡量学生综合解题能力以及数学素养．下面举例讲评．

图1

(1) 求椭圆的方程;

(2) 设直线AC、BD斜率分别为k1、k2,求k1+k2.

1 阐述题意

本题是一道解析几何综合题,以直线和椭圆为载体,主要考查椭圆的标准方程、直线的斜率、直线与椭圆的位置关系等基础知识.通过椭圆中的定点、定值问题综合考查运算求解能力和推理论证能力.

已知条件:椭圆的焦点坐标及半焦距、离心率,线段OE=EF. 隐含条件:∠EOF=∠EFO,A、B关于原点O中心对称,线段CD为焦点弦. 问题:直线AC、BD的斜率分别为k1、k2,求k1+k2的值.

学生的难点: 1)在带字母的运算中,不注重算理的分析,不能使算法更合乎逻辑. 2)处理解析几何问题的核心方法是将所涉及的几何问题代数化,通过代数运算,解决几何问题,其中重要的一点是加强对问题的代数转化能力,线段OE=EF这个等式内容丰富,可利用角度多,怎么使用?学生很难准确选用. 3)在解决本题的过程中选择不同的解题策略,运算量差距较大,如何在解题的过程中多角度地获取信息、运用信息,进而选择恰当的解题路径.

本题对学生的运算能力,特别是算理分析有相当高的要求,思维量较大,属难题.

学生的易错点: 1)线段CD过点F,学生易简单理解为过定点的直线,而忽略焦点弦的特征. 2)简单的罗列关系、互相代换导致运算复杂化,算不出结果. 3)没有解题思路,只知道套用公式,无法将题目中的条件进行代数转化,而使解题无法继续.

2 题目背景

从知识立意的角度分析,本题主要考查直线的斜率与方程、椭圆的方程和几何性质,利用方程判定曲线的性质以及圆锥曲线中的定点问题等.

从能力立意的角度思考,本题对符号运算能力要求较高,要求学生具有较强的分析、论证能力.侧重考查学生发现问题、分析问题、解决问题的能力,抽象概括能力,数与形转化的能力,运算求解能力和推理论证能力,对知识的运用和迁移的能力等.对学生的数学直觉、直观思维的敏捷性、演绎推理的逻辑性等.

试题的几何背景来自于圆:在如图2所示的圆中,因为∠1+∠2=∠3=∠4=∠5=∠6+∠7,且∠2=∠7,所以∠1=∠6.把上述结论推广到椭圆中研究.试题的设计在注重基础的前提下,充分体现了解析几何的思想方法,强调了从学科的思想体系的角度去认识、把握知识和方法.

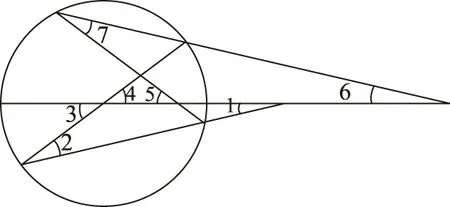
图2

3 题目解答

x2/2+y2=1.

①

(2)方法1设直线AB的方程为

y=kx,

②

则直线CD的方程为

y=-k(x-1),

③

由式①、②得

(2k2+1)x2=2.

④

由式①、③得

(2k2+1)x2-4k2x+2k2-2=0.

⑤

记A(x1,kx1),B(x2,kx2),C(x3,k(1-x3)),D(x4,k(1-x4)),则直线AC、BD的斜率之和

又由式④、⑤可知

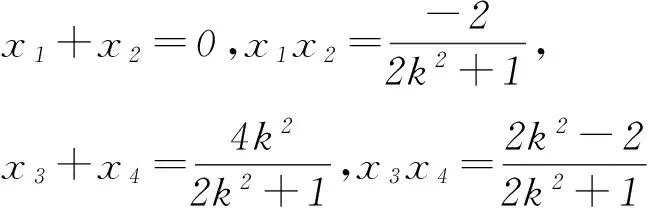
则k1+k2=0.

⑥

则直线CD的方程为

⑦

由式①、⑦得

⑧

则直线AC、BD的斜率之和

方法3先取CD垂直与x轴的情况,判断k1+k2=0,然后代入验证.

4 总结提炼

处理圆锥曲线问题的精髓是将平面图形坐标化,核心方法是将所涉及的几何问题代数化,通过代数运算,解决几何问题.形与数的恰到好处地整合能有效促进思维链的自然生长,学生借助于图形直觉选择问题情境的某些特征,确定所要探索的变量关系的各种可能性,并整体把握问题解决的方向.依靠代数定量分析演绎推理论证猜想,细化完善思路,从而使思维链得到有效延伸.在形与数2种不同形式的问题表征下,问题解决的脉络会更清晰,效率会更高,方向会更准确.要培养学生有效控制运算失误,注重数学符号运算变形和算理分析,尤其是合乎情理的算法的逻辑评估.要引导学生重视做题后的感悟,不仅要关注一题多解,更要能“闻一知十”,进行反省性抽象归纳、概括.

福建省安溪第六中学)