挖掘几何性质 巧解解析几何问题

◇ 安徽 陈芬梅 吴刘维



挖掘几何性质 巧解解析几何问题

◇ 安徽 陈芬梅1吴刘维2

解析几何是高考的必考内容,有些问题对运算能力要求非常高,用坐标法求解解析几何问题时,规律性强,思路比较简单,但运算过程烦琐．在一些解析几何问题中若能挖掘出题设中图形的几何特征,并且充分利用平面几何的有关性质,常常会降低解题难度,得到简捷而巧妙的解法．本文简举几例,利用平面图形的几何性质巧妙地解决解析几何问题,意在培养学生运用几何性质优化解析几何计算的意识．

1 利用几何性质巧解圆的问题

图1

例1如图1,已知圆O与坐标轴的3个交点分别为A(-1,0)、B(2 016,0)、C(0,-2),则该圆与坐标轴的第4个交点D点的坐标为________.

解析设圆的一般方程为x2+y2+Dx+Ey+F=0 (D2+E2-4F>0)将A(-1,0)、B(2 016,0)、C(0,-2)代入圆方程得

所以圆的一般方程为

x2+y2-2 015x-1 006y-2 016=0.

再令x=0得y=-2或1 008, 由题意y=-2(舍),所以D点坐标为(0,1 008),此法计算量较大.

利用几何性质: 利用平面几何中圆的相交弦定理有|OA|·|OB|=|OC|·|OD|,所以

由题意可知D(0,1008),简单快捷求得结果．

2 利用几何性质巧解椭圆问题

解析如图2所示,欲证∠AMF=∠BMF,可证kAM=-kBM,由于A、B2点是变化的且坐标未知,所以运算较烦琐.

图2

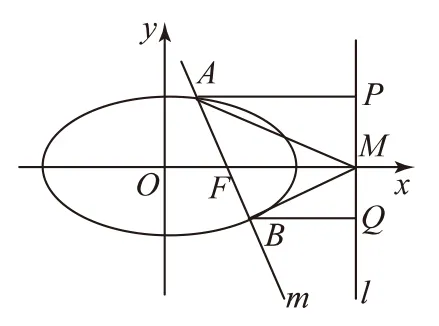
图3

3 利用几何性质巧解抛物线问题

例3已知点A(2,0),抛物线C:x2=4y的焦点为F,直线FA与抛物线C相交于点M,与其准线相交于点N,则|FM|∶|MN|=( ).

图4

图5

思路简单,然而这种方法的运算过程较为烦琐.

4 利用几何性质巧解双曲线问题

图6

解析利用几何性质:由题意可知F1(-c,0)、F2(c,0)，如图6. 设△PF1F2内切圆的圆心在x轴上的投影点为A(x,0),此内切圆分别与PF1、PF2切于点M、N, 由切线长定理知

|PM|=|PN|, |F1M|=|F1A|, |F2A|=|F2N|.

结合图形由双曲线的定义知|PF1|-|PF2|=2a,所以(|PM|+|F1M|)-(|PN|+|F2N|)=2a,故|F1A|-|F2A|=2a. 而|F1A|+|F2A|=2c,所以|F1A|=c+a, |F2A|=c-a, |OA|=a,得出x=a．

总之,在遇到可以用几何性质优化计算的解析几何问题时,要有利用几何性质优化解析几何计算的意识,要努力克服重思路方法,轻计算技巧的顽症,事实上这些策略也不是孤立的,在具体解题过程中,往往需要综合考虑,相互补充,才能收到变难为易、化繁为简、事半功倍的效果．