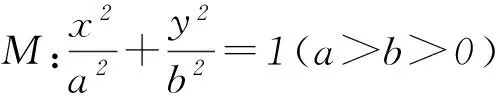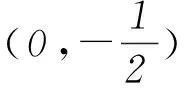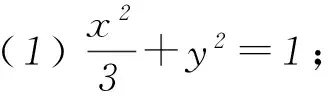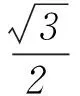抛物线问题的多角度探究
◇ 江苏 韩小波
抛物线问题的多角度探究
◇ 江苏 韩小波
与抛物线有关试题的命制通常以直线与抛物线相交为背景,考查点主要包括弦长、与焦点或准线有关的平面图形的面积、定点、定值等问题.问题处理的常规方法利用坐标法,将几何问题代数化处理.本文以一道直线与抛物线的综合问题为例,就其中所涉及的解题方法、技巧等进行深入分析.
1 题目赏析
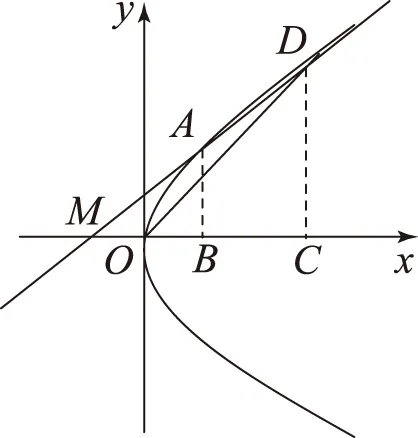
例已知点A(x1,y1)、D(x2,y2) (其中x1 (1) 当点B的坐标为(1,0)时,求直线AD的斜率; 本题背景为直线与抛物线相交,问题涉及2交点与抛物线顶顶点构成的三角形面积问题. 第(1)问题较为基础,解答略.下面对第(2)问从多角度探究. 2.1 利用分割法 图1 如图1,设直线AD与x轴交点为M,△OAD的面积可由△OMD的面积减去△OMA的面积,而这2个三角形的底边相等,均为|OM|,则面积差问题转化为2个三角形高的差的问题,进而转化为A、D2点纵坐标差的问题,即|y2-y1|,再利用直线方程将y1、y2用x1、x2表示,结合已知条件求解. 方法1设直线AD的方程为y=kx+m,则 因为Δ=16-16km>0,所以0 2.2 利用弦长公式 三角形面积的求解除了分割法以外,还可利用弦长公式直接求出△OAD的底边|AD|的长,再利用点到直线的距离公式求出三角形的高h,进而直接求面积. 方法2设直线AD的方程为y=kx+m. 因为Δ=16-16km>0,所以0 2.3 点差法,设而不求 ① 此类问题的处理方法也可推广到椭圆或双曲线问题中,如下面的变式题. (1) 求椭圆M的方程; 因篇幅所限,过程略,请同学们按文中例题所述方法进行求解. 通过对一道问题的多角度分析,能有效考查学生基础知识的掌握程度以及灵活应用所学内容分析问题、解决问题的能力. 江苏省南京市溧水区第三高级中学)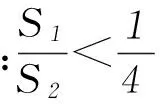
2 解法探究
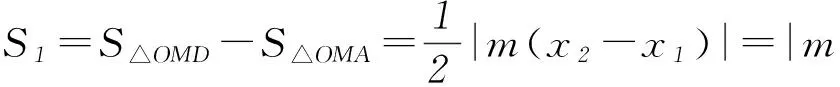
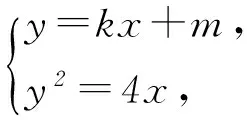
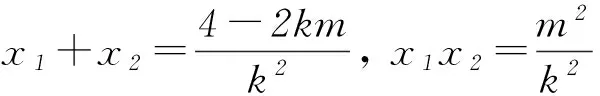
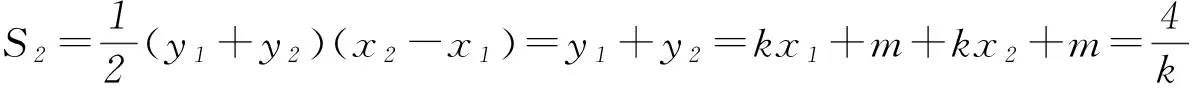
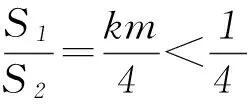
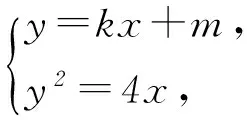
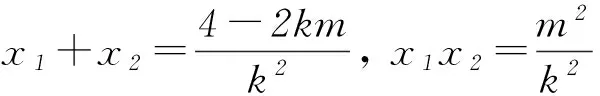
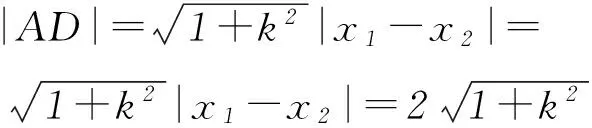
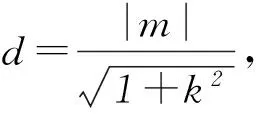
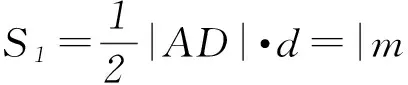
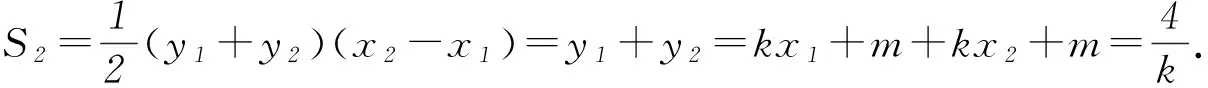
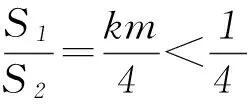
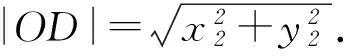
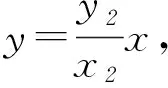
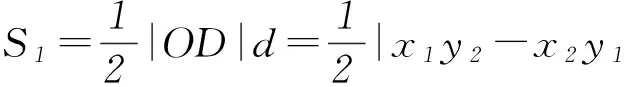
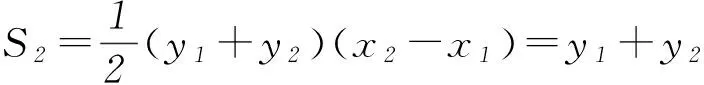
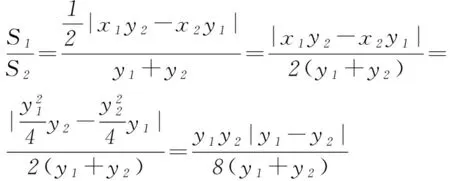
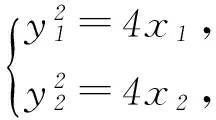
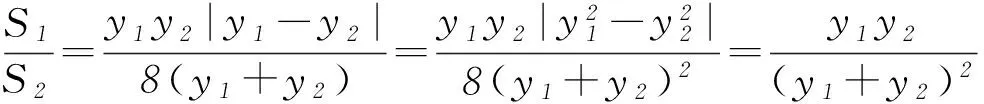
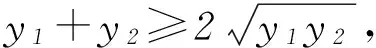
3 变式演练