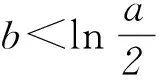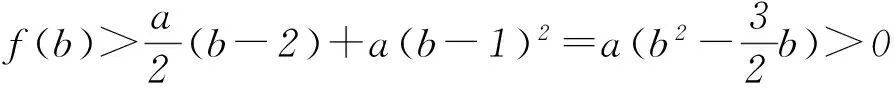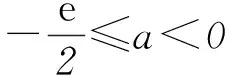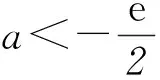2016年高考数学卷导数综合题解析
◇ 北京 王保东(特级教师) 相文明
2016年高考数学卷导数综合题解析
◇ 北京 王保东1(特级教师) 相文明2
导数综合题均采用“多问把关”的形式,一般涉及曲线的切线方程、函数的性质,以及相关不等式的证明等问题.其核心是通过导数的单调性和局部判断等手段得到适当的函数图象,达到“以图启数、以数论形”的目的.在高考中,导数综合题都是中档题和较难题,突出考查函数与方程、等价转化、数形结合、分类与整合、有限与无限等思想方法和探索精神,对学生具有的数学思想方法、利用数学知识分析问题和解决问题的能力、数学学科素养都有很高的要求.
1 利用二次求导,弄清函数性质
利用导数解决函数问题时,一般步骤为确定函数的定义域;求函数的导数;判定导函数的零点或导函数的符号;确定原函数的图象.在今年的高考试题中,许多学生在求导函数的零点时遇到障碍,求导函数的零点需要解超越方程,而超越方程没有一般的求解方法,这时就要换个角度想问题,把导函数或导函数变形后的部分看成一个新函数,再对新函数求导,通过研究新函数的性质,把握原函数的性质.这个过程,通常被称为“二次求导”.在无法判定导函数的零点或导函数的符号时二次求导就显得尤为重要,它会使解题方向峰回路转,收到意想不到的效果.
例1(2016年北京卷理科18题) 函数f(x)=xea-x+bx,曲线y=f(x)在点(2,f(2))处的切线方程为y=(e-1)x+4.
(1) 求a、b的值;
(2) 求f(x)的单调区间.
解析(1) 因为f(x)=xea-x+bx,所以
f′(x)=(1-x)ea-x+b.
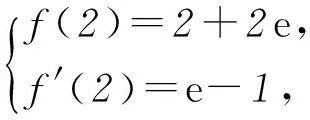
(2) 由(1)可知f(x)=xe2-x+ex,f′(x)=e2-x(1-x+ex-1).由e2-x>0,可知f′(x)与1-x+ex-1同号.
令g(x)=1-x+ex-1,则g′(x)=-1+ex-1.所以,当x∈(-∞,1)时,g′(x)<0,g(x)在区间(-∞,1)上单调递减;当x∈(1,+∞)时,g′(x)>0,g(x)在区间(1,+∞)上单调递增.故g(1)=1是g(x)在区间(-∞,+∞)上的最小值.
从而g(x)>0,x∈(-∞,+∞).
综上f′(x)>0,x∈(-∞,+∞).
故f(x)的单调递增区间为(-∞,+∞).
点评本题第(1)问考查导数的几何意义——切线问题,它在选择题、填空题和解答题中都有可能出现.解题的关键是抓住切点,没给切点的要先设出切点坐标(x0,y0),再利用切点处的导数等于切线的斜率和切点是原函数的图象与切线的公共点构造方程组求解.第(2)问是求函数的单调区间问题,按照解题步骤在解导数大于零和导数小于零时遇到了困难,此时,将导函数中符号不确定的因式构造成新函数,进行二次求导,结合第二次导函数的正、负,很好地解决了一次导数的正、负问题,进而解决了原函数的单调区间问题.
2 利用承上启下,巧妙解决问题
高考主要考查学生数学知识、思想方法、思维能力和数学素养.试题既重基础,又体现灵活创新,但考场上时间是有限的,盲目套用成题模式,往往会事倍功半.所以做高考解答题时要关注一道题的前后之间、上下问之间是否有联系,许多试题在问题与问题之间是相互联动、普遍联系的,前面问题的解决对后面问题的解决是有影响和帮助的.
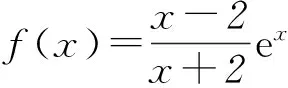
(x-2)ex+x+2>0.
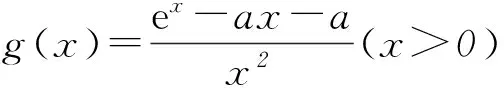
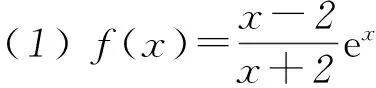
(-∞,-2)∪(-2,+∞),
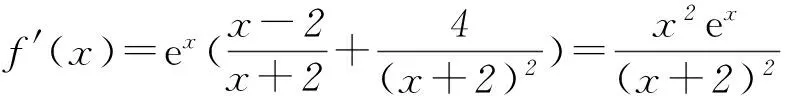
因为当x∈(-∞,-2)∪(-2,+∞)时,f′(x)≥0.所以f(x)的单调增区间为(-∞,-2)、(-2,+∞).
思路1构造新函数,二次求导.
设h(x)=(x-2)ex+x+2,x>0,则
h′(x)=ex+(x-2)ex+1=(x-1)ex+1.
令m(x)=h′(x)=(x-1)ex+1,则
m′(x)=ex+(x-1)ex=xex.
因为当x>0时,m′(x)>0,故m(x)的单调增区间为(0,+∞),且m(0)=0.所以当x>0时,m(x)>0,即h′(x)>0.所以h(x)的单调增区间为(0,+∞),且h(0)=0.所以当x>0时,h(x)>0,即当x>0时,(x-2)ex+x+2>0.
思路2观察函数f(x)与欲证不等式,建立联系.
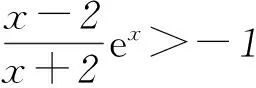
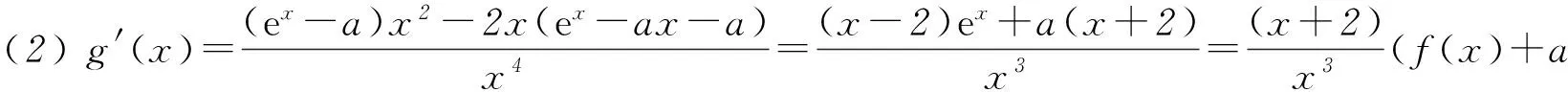
由(1)知,f(x)+a在(0,+∞)上单调递增.
对任意a∈[0, 1),f(0)+a=a-1<0,f(2)+a=a≥0. 因此存在唯一的t∈(0, 2],使得f(t)+a=0,即g′(t)=0.
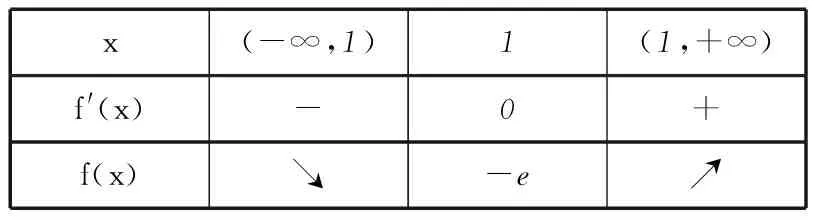
当0 当x>t时,f(x)+a>0,g′(x)>0,g(x)单调递增. 因此g(x)在x=t处取得最小值 点评本题第(1)问判断函数单调性,考查“乘积函数”和“商”函数的导数运算法则,虽然属于基础知识、基本方法和基本技能,但有一定的综合性,求解过程突出对运算能力的考查,关注数学的核心素养;在证明不等式时,把它看成一个独立的问题,构造新函数,并采用二次求导的方法解决.但是观察到所证不等式就是f(x)>f(0)的变形,自然会用函数单调性求解.第(2)问看似是一个熟悉的求最值问题,一旦动手,发现困难重重,即使直接运用二次求导也不易求解.只有认真观察,将函数g′(x)进行拆分,借助函数f(x)的性质才能解决.题目在常规问题中体现着不平凡的设计理念,对突破模式化教学具有很好的引领作用. 在导数的应用中,最基本的是由导函数的符号判断原函数的增减,得到原函数的“草图”,但这个“草图”是否真的可靠,还需要对图象的边界点,以及变化趋势加以定性和定量分析,才能整体把握函数图象的变化规律,正确解决所求问题. 例3(2016年全国乙卷理科21题) 已知函数f(x)=(x-2)ex+a(x-1)2有2个零点. (1) 求a的取值范围; (2) 设x1、x2是函数f(x)的2个零点, 证明:x1+x2<2. 解析(1)f′(x)=(x-1)ex+2a(x-1)= (x-1)(ex+2a). 当a=0时,f(x)=(x-2)ex,函数f(x)只有1个零点. 当a>0时,f′(x)与f(x)的关系如表1. 表1 所以f(x)在(-∞,1)单调递减,在(1,+∞)内单调递增,fmin(x)=f(1)=-e<0. 又f(1)<0,且f(x)在(-∞,1)单调递减,所以在(-∞,1)上存在唯一的零点.故f(x)存在2个零点. 当a<0时,由f′(x)=0得x=1或x=ln(-2a). 又当x≤1时,f(x)<0.所以f(x)不存在2个零点. 当1 当x>ln(-2a)时,f′(x)>0,f(x)单调递增. 又当x≤1时,f(x)<0.所以f(x)不存在2个零点. 综上所述,当且仅当a>0时符合题意,即a的取值范围为(0,+∞). (2) 不妨设x1 x1∈(-∞,1),x2∈(1,+∞),2-x2∈(-∞,1), f(x)在(-∞,1)单调递减.所以x1+x2<2 等价于f(x1)>f(2-x2),即f(2-x2)<0. 由于f(2-x2)=-x2e2-x2+a(x2-1)2,而 f(x2)=(x2-2)ex2+a(x2-1)2=0, 所以f(2-x2)=-x2e2-x2-(x2-2)ex2. 设g(x)=-xe2-x-(x-2)ex, 则 g′(x)=(x-1)(e2-x-ex). 所以当x>1时,g′(x)<0,而g(1)=0,故当x>1时,g(x) 从而g(x2)=f(2-x2)<0,故x1+x2<2. 点评在第(1)问a>0的讨论过程中,可知函数f(x)在(-∞,1)内单调递减,在(1,+∞)内单调递增,再结合f(1)=-e<0,有些学生就会据此得到函数一定有2个零点.针对本题,结果是正确的,但说理是不严谨的,还需说明在(-∞,1)和(1,+∞)上分别存在函数值大于零的x值,才能确定函数f(x)有2个零点.出错的原因是对函数f(x)图象的把握不够准确,只有综合考虑函数的极值、最值、单调性以及图象的变化趋势才能得到函数的“真”图.在a<0的讨论过程中,我们先研究函数单调性,再借助函数解析式对函数值进行局部判断,得到当x≤1时,f(x)<0,就能得到合适的“草图”,而这个“草图”对解决当前问题足够用了.这种“判断函数值在某部分的符号,并结合函数单调性,得到‘草图’”的方法可以简化运算,在许多高考题中都有体现.在第(2)问中,通过函数的单调性,把x1+x2<2等价转化为f(x1)>f(2-x2)是解决问题的关键. 通过以上导数高考题的分析,清晰地看到对导数题的考查万变不离其宗.所以高考复习过程中,考生面对给出的题目,首先是弄明白要解决的问题是什么,它能转化成什么问题;接下来是思考为了解决上面的问题,有可能用到的函数是什么,学生要有根据问题构建恰当函数的意识和基本方法;研究上面构建出来的函数(一般要借助导数).导数的考查不只停留在利用导数研究函数性质的层面,要能够利用所构建的函数的性质去解决问题. 导数题综合性强,对数学思想和数学运算能力的要求都很高,复习中不可能一步到位,应该循序渐进,从而更好地提高学生学习数学的自信心和解决数学问题的能力. 建议在高三第1轮复习时,注意以下3点: 1) 重视基础,把复习落到实处. 理解基础要到位,记忆公式要准确,运用知识要灵活,设计活动要合理,复习才能落到实处. 2) 重视表述,使复习讲求实效. 重视书写的规范性、思维的严谨性、表述的合理性,不要让会做不会写成为复习路上的绊脚石. 3) 重视方法,让复习有规可循. 恒成立问题(存在性)问题,优先分离变量;不等式证明转化为函数最值问题;解导数为零的方程有障碍时,采取二次求导等.熟悉常见的解题策略,明确解题方向,达到事半功倍的效果. (注:本文为“北京市教育学会‘十三五’教育科研课题:‘互联网+’下高中数学青年教师课堂教学行为研究”成果之一.)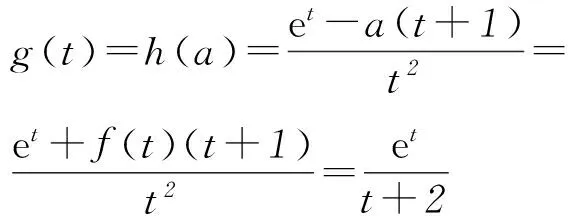
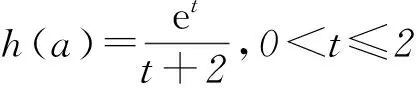
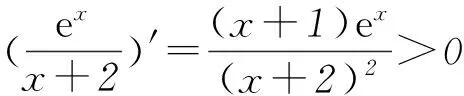
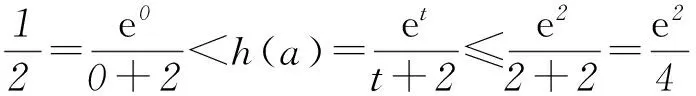
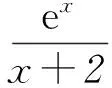
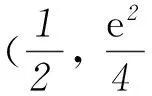
3 利用局部判断,弄清变化规律