基于多分布GARCH族模型的沪深300指数VaR测度研究

刘桂荣，周伟杰

( 1.齐鲁工业大学 工商学院，山东 济南 250535； 2.潍阴工学院 管理工程学院，江苏 淮安 223030)

金融研究

基于多分布GARCH族模型的沪深300指数VaR测度研究

刘桂荣1，周伟杰2

( 1.齐鲁工业大学 工商学院，山东 济南 250535； 2.潍阴工学院 管理工程学院，江苏 淮安 223030)

运用经济物理学方法验证沪深300指数市场存在的一些特征，进而用四种GARCH模型在不同分布下进行VaR风险测度建模，并用返回测试中的似然比和动态分位数回归加以检验，结果表明：收益分布服从有偏学生t分布的VaR测度模型可靠性显著高于正态分布和学生t分布；在样本内，GARCH、GJR、HYGARCH模型均能有效度量VaR风险，HYGARCH在空头VaR水平较高时精度更高；在样本外，GARCH、GJR、FIGARCH、HYGARCH模型的VaR测度能力相差不大，但HYGARCH模型在空头VaR水平下测度能力更高些。因此，在有偏学生t分布下，能捕捉更多金融资产特征的HYGARCH模型对沪深300指数的VaR测度更精确可靠，这意味着在风险管理时，应更多考虑具有尾部效应的模型进行度量。

GARCH族模型； VaR测度；返回测试；风险测度；金融风险；股票指数；期货投资

一、引 言

风险管理是金融市场重点研究方向之一，定量上一般用VaR来测度市场风险，VaR测度的准确与否在于对资产收益分布与其波动能否正确刻画。一直以来，金融资产或其组合都是以“有效市场假说(Efficient Market Hypothesis,EMH)”理论为基石。但从20世纪70年代以来，随着计算机技术的突飞猛进，特别是以实际数据为出发点的经济物理学的发展，越来越多的实证研究证实金融市场存在EMH解释不了的特征，如收益率的尖峰、有偏厚尾分布、波动率的长记忆性，以及收益率和波动率都存在的分形和多重分形特征等①Mantegna,R.N.and H.E.Stanley:Scaling behaviour in the dynamics of an economic index,376(6535),pp.46-49，1995.②Kantelhardt,J.W.,S.A.Zschiegner,E.Koscielny-Bunde,S.Havlin,A.Bunde and H.E.Stanley:Multifractal detrended fluctuation analysis of nonstationary time series,Physica A:Statistical Mechanics and its Applications,316(1-4),pp.87-114,2002.③McNeil,A.J.and R.Frey:Estimation of tail-related risk measures for heteroscedastic financial time series:an extreme value approach,Journal of Empirical Finance,7(3-4),pp.271-300,2000.。这使得长期以来金融资产在正态分布下的风险度量受到挑战。

近年来，有学者利用学生t分布来对收益分布结构刻画，尽管它比正态分布更能捕捉收益的长尾特征，然而它不能刻画收益的有偏性，为此，Giot和Laurent引入有偏学生t分布(Skew Student t Distribution,

SKST)对金融资产收益分布进行建模分析*Giot,P.and S.Laurent:Value-at-risk for long and short trading positions,18,pp.641-663,2003.。准确刻画资产收益分布是VaR测度正确的前提，除此之外，对金融资产条件波动率模型的选取也是VaR计量精确的关键。对于条件波动率的刻画，Bollerslev在Engle基础上提出的广义自回归条件异方差(GARCH)模型是最基本也是最经典的模型*Bollerslev,T.：Generalized autoregressive conditional heteroskedasticity,Journal of Econometrics,31(3),pp.307-327,2000.。此后，针对金融资产收益不同特征，学者们又提出了许多改进模型，例如根据波动非对称杠杆效应的EGARCH、GJR、非对称幂GARCH(APGARCH)、非线性GARCH(NAGARCH)等模型，此外，人们发现收益波动也存在持续性，为此，刻画其长记忆的模型，如FIGARCH、FIEGARCH、FIAPGARCH等模型也在近几年逐步提出，其中长记忆HYGARCH模型对金融资产收益的各种特征适应性更广些*Davidson,J.：Moment and Memory Properties of Linear Conditional Heteroscedasticity Models,and a New Model,Journal of Business & Economic Statistics,22(1),pp.16-29,2004.。

即使对于同一资产，不同模型的VaR风险测度也存在一些差别。徐炜和黄炎龙用GARCH类模型对上证综指日收益率进行分析，发现FIGARCH、FIEGARCH、IGARCH模型能较好的度量VaR*徐炜，黄炎龙：《GARCH模型与VaR的度量研究》，《数量经济技术经济研究》，2008年第1期。。魏宇以上证综指和世界若干股指为例，以RISKMETRICS、GARCH、APARCH对其风险建模，发现在有偏学生t分布下的VaR风险测度更有效，但是能捕捉市场非对称信息的APARCH模型没有表现出比GARCH更高的精度*魏宇：《有偏胖尾分布下的金融市场风险测度方法》，《系统管理学报》，2007年第3期。。林宇等发现用FIAPARCH-SKST模型对上证综指VaR测度，其精度要好于RISKMETRICS、GARCH模型*林宇，卫贵武，魏宇，谭斌：《基于Skew-t-FIAPARCH的金融市场动态风险VaR测度研究》，《中国管理科学》，2009年第6期。。曹广喜等以上证综指和深圳成指为样本，以GARCH族模型建模，结果表明FIAPARCH和HYGARCH分别对股市VaR测度、股市涨跌有较好的预测性*曹广喜，曹杰，徐龙炳：《双长记忆GARCH族模型的预测能力比较研究——基于沪深股市数据的实证分析》，《中国管理科学》，2012年第2期。。王宜承和陈艳考虑了上海银行间同业拆借利率(Shibor)的分形特征，认为ARFIMA-FIGARCH模型对Shibor的VaR风险度量更精确*王宣承，陈艳：《基于ARFIMA-FIGARCH 模型的利率市场风险度量》，《统计与信息论坛》，2014年第6期。。

沪深300指数是沪深证券交易所于2005年4月8日联合发布反映A股市场整体走势的指数，它选择了上海和深圳证券市场中的300只A股作为样本，能较好的代表中国股票市场总体特征，同时它也是中国第一只金融期货—股指期货标的物。因此，沪深300指数的风险测度无论对于一般市场投资或股指期货投资者都有十分重要的作用。

基于此，本文首先利用经济物理学的方法验证沪深300指数的一些特征，进一步用GARCH族模型对沪深300指数进行样本内和样本外VaR测度分析，并用返回测试中严格的似然比测试和动态分位数回归对模型在不同分布下的风险测度精度进行后验分析*Kupiec,P.H.：Techniques for Verifying the Accuracy of Risk Measurement Models,Journal of Derivatives,3(2)，1995.*Engle,R.F.and S.Manganelli：CAViaR:Conditional Autoregressive Value at Risk by Regression,Quan Journal of Business and Economic Statistics,22(4),pp.367-381，2004.，以找出适合沪深300指数的风险度量模型。与现有文献相比，本文应用经济物理学中的理论方法验证了沪深300指数存在的典型市场特征，进而结合这些特征构建计量模型，使得模型建立有据可循；同时在不同分布和不同模型双重情形下选择出沪深300指数的最优VaR测度模型。

二、计量模型与方法

(一)VaR测度模型

在沪深300指数收益率滚动建模时，考虑了多种模型，综合考虑收益特征、模型的收敛性以及模型的AIC和SIC值，均值方程选Rt=μt+εt，(Rt=lnPt-lnPt-1)为沪深300指数收益率)；波动方程选GARCH、GJR、FIGARCH、HYGARCH四种波动率模型，GARCH项和ARCH项的滞后阶数为1。其余模型，如EGARCH、APARCH、FIEGARCH、FIAPGARCH等在建模时，发现模型参数估计收敛性很差，甚至不收敛，这样得到的VaR测度也很差，故排除；对于均值方程，如采用ARMA，发现所得的结果与上述均值方程结果类似。因此，为了方便起见，选择Rt=μt+εt。

1.GARCH(1，1) 模型

均值方程：Rt=μt+εt=μt+σtzt，zt～iid(0，1)

(1)

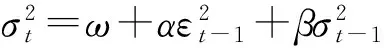
(2)

2.GJR(1，1) 模型*Glosten,L.R.,R.Jagannathan and D.E.Runkle：On the Relation between the Expected Value and the Volatility of the Nominal Excess Return on Stocks,48,pp.198-219，1993.

均值方程与GARCH(1，1)相同，波动方程为：

(3)

3.FIGARCH模型*Baillie R.T.,Bollerslev,T.,Mikkelsen H.O.：Fractionally integrated generalized autoregressive conditional heteroskedasticity.Journal of Econometrics,vol.73,3-20.1993.

均值方程与GARCH(1，1)相同，波动方程为：

(4)

4.HYGARCH模型*Davidson,J.:Moment and Memory Properties of Linear Conditional Heteroscedasticity Models,and a New Model,Journal of Business & Economic Statistics,22(1),pp.16-29,2004.

均值方程与GARCH(1,1)相同，波动方程为：

(5)

在上述四类波动方程中，α为ARCH效应系数，β为GARCH效应系数，γ为非对称波动杠杆效应系数，d为长记忆系数，L为滞后算子。在HYGARCH模型中，若，HYGARCH退化为FIGARCH模型，若φ=0，HYGARCH退化为GARCH模型。在建模时，均值方程中的μt令为常数，波动方程FIGARCH、HYGARCH为长记忆GARCH类模型，GJR模型可以刻画收益波动的非对称杠杆效应。

(二)VaR估计方法

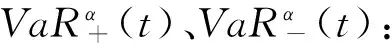
(6)

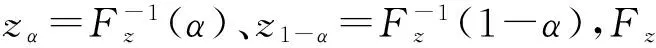
(7)

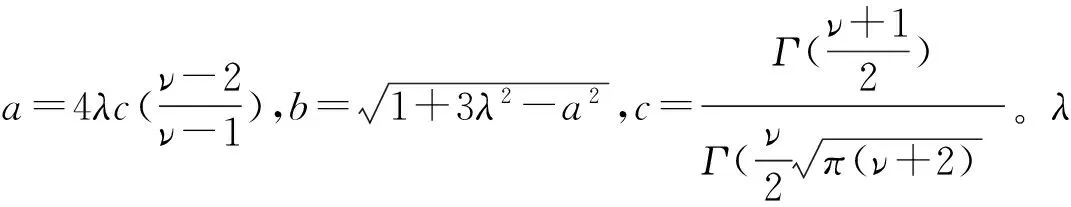
(三)VaR测度准确性检验方法

风险管理的的作用在于是否准确地估计风险。VaRα(t)是α给定置信度下的风险估计值，当VaRα(t)>Rt即可认为在置信度α下t时刻的风险估计是有效的，反之则是失败的，为此，可以用失败率对VaR估计效果进行检验。设失败率f为实际观测值大于在置信水平α下的VaR的个数(N)占整个观察期(T)的比率。VaR估计效果的好坏可以用与置信水平是否接近来比较。若二者在统计意义上十分接近，则认为VaR估计是有效的，反之无效。Kupiec认为失败次数之和服从伯努利二项分布，为此构造如下假设H0∶f=α，并用似然比的非条件检验统计量(Kupiec LR，LR)*Kupiec,P.H.Techniques for Verifying the Accuracy of Risk Measurement Models,Journal of Derivatives,3(2).1995.：

LR=2(log(fN(1-f)T-N)-log(αN(1-α)T-N))～χ2(1)

(8)

对原假设进行检验，若统计量LR显著，则接受原假设，即VaR估计是有效的。

研究表明，VaR失败有可能存在相关的情况，若VaR失败连续发生，则有可能使投资者连续出现超过VaR的损失，则说明VaR估计模型是不可靠的，准确可靠的VaR模型即使出现失败的情形也应该是不相关的。为此，Engle和Manganelli(2004)用动态分位数回归来检验VaR模型，其统计量为(Dynamic quantile regression,DQR)*Engle,R.F.and S.Manganelli:CAViaR:Conditional Autoregressive Value at Risk by Regression,Quan Journal of Business and Economic Statistics,22(4),pp.367-381,2004.：

(9)

其中X是T×K矩阵，服从自由度为K的卡方分布，取K=7。若在置信水平下统计量不显著，说明风险测度模型是可靠的。

在我国股票市场，投资者基本上都是进行多头操作，而在期货市场可以对资产进行多空操作。由于一方面对资产的多空VaR测度分析不仅仅在于求出最大风险损失，其本质是对资产下跌和上涨的预测度量；另一方面沪深300指数是股指期货标的物，二者之间相互关联，价格走势基本一致，且存在价格引导关系，因此尽管沪深300指数是股票指数，不存在空头操作，但对沪深300指数多空VaR分析可为整个股票市场未来走势和期货投资的风险管理提供帮助。下文将用以上模型对沪深300指数多空VaR进行度量以及精度分析。

三、实证分析

(一)样本选择及描述

本文选取沪深300指数自2005年4月8日上市至2014年8月31日的日收盘价作为研究对象，共有2265个数据，用第2节收益率公式计算沪深300日收益率。VaR测度建模即为上述四类GARCH模型和均值方程模型，选正态(N)、学生t、有偏学生t(SKST)分布作为收益率分布形式，这样对一组数据建模共有12种方式。本文对VaR测度模型的估计分为样本内和样本外，样本内取收益率序列前1200个数据进行估计；样本外采用滚动的方式进行：第一次用前1200个数据建模向前一步预测VaR，并与原始序列第1201个数据比较，第二次用第2-1201个数据建模向前一步预测VaR，并与原始序列第1202个数据比较，即每次向前滚动一步，数据长度保持不变(1200)，对其建模向前一步预测，并与这组数据的前一个数比较，这样反复进行，直至第2263个数据。预测的个数一共为1074个。为了说明金融资产数据存在的特征，本文用经济物理学方法以第一组样本为例进行验证，其它样本性质是类似的。

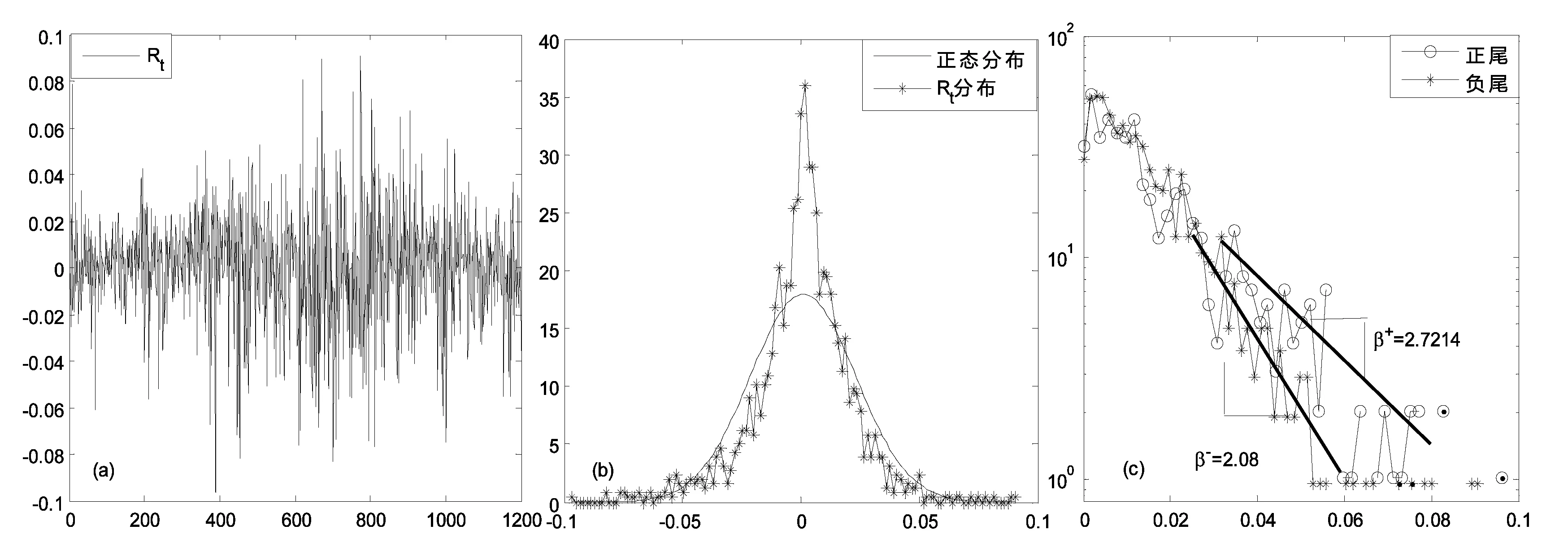
图1 收益率序列及其分布

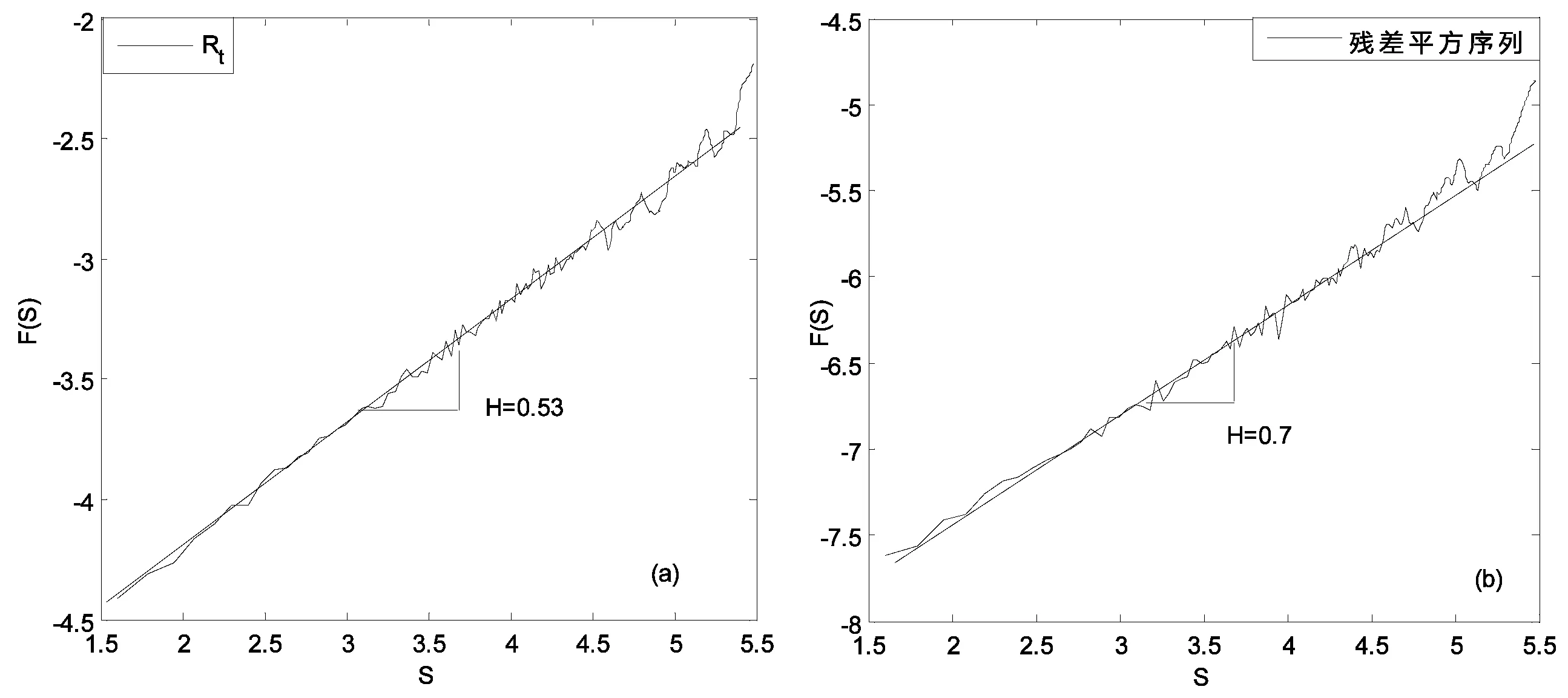
图2 收益率及其残差平方序列的Hurst指数

图1为沪深300收益率序列及其分布，从图1(b)可以看出，收益分布具有尖峰厚尾性，通过计算，收益序列的偏度和峰度分别为-0.4和4.98，JB统计量的p-值几乎接近0，表明收益率序列偏离正态分布。根据经济物理学家Mantegna提出的方法*Mantegna R N,S.H.E.:Introduction to econophysics:correlations and complexity in finance,Cambridge university press,2000.，计算出沪深300收益率的中心服从平稳Lévy分布，α=1.54。同时，利用Hill估计*Hill,B.M.:A Simple General Approach to Inference About the Tail of a Distribution,The Annals of Statistics,3(5),pp.1163-1174,1975.，估算出沪深300的左尾和右尾均具有幂律分布性，其标度指数分别为β+=2.72和β-=2.08，见图1(c)，这也进一步说明了收益率分布的不对称性。尾部指数的不一致，说明当VaR水平较高时，即面临的损失较大时，空头和多头的VaR是有差异的。利用经典的去趋势波动法(DFA)*Peng,C.K.,S.V.Buldyrev,S.Havlin,M.Simons,H.E.Stanley and A.L.Goldberger:Mosaic organization of DNA nucleotides,Phys.Rev.E,49,pp.1685-1689,1994.(通过数值模拟，Jeong等已检验出DFA是目前估计序列长记忆性的一种较好的方法*Jeong H D J,Lee J S R,McNickle D,et al:Comparison of various estimators in simulated FGN.Simulation Modeling Practice and Theory,15:1173-1191,2007.)，计算出收益率序列的Hurst指数为0.53，基本上不存在长记忆性，为此在序列均值方程建模时，可不考虑长记忆模型(如ARFIMA模型)。图2(b)为经均值方程过滤后的残差序列平方，其Hurst指数为0.7，暗示存在长记忆，在波动率建模时需要将该特征考虑在内。

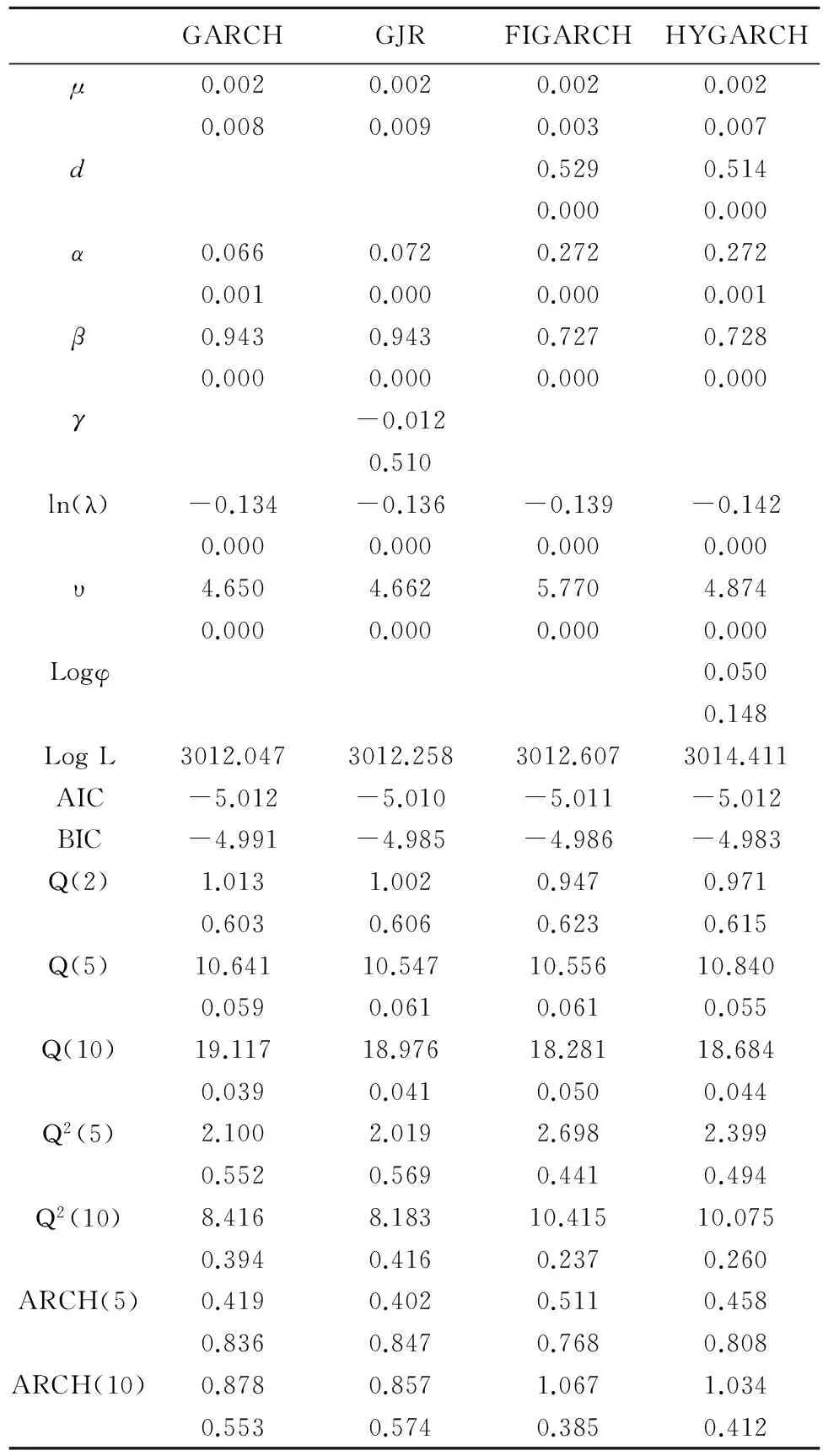
表1 沪深300收益率的GARCH类—SKST模型参数

(二)VaR风险测度模型的参数估计

本文采用拟极大似然法(QMLE)估计各个模型参数，表1给出了样本内GARCH、GJR、FIGARCH、HYGARCH模型在收益分布服从有偏学生t分布下的参数估计及其残差检验，其余分布由于篇幅所限，未给出模型参数估计值。在每个参数的下方数值为其p-值，可以看出大多数参数在置信水平1%下显著。在建模时，发现波动方程中的常数项几乎在所有预测样本下都不显著，将常数项加入有时反而影响模型参数估计的收敛性，为此，建模时未将常数项加入。FIGARCH、HYGARCH中的长记忆参数d在1%下显著，印证残差平方序列的长记忆性。此外从GJR模型的系数可知，沪深300指数在研究期内的非对称杠杆效应并不显著。对残差序列的自相关检验(Q(2)、Q(5)、Q(10))，残差平方(Q2(5)、Q2(10))检验，以及残差的ARCH效应检验表明对沪深300收益序列所建模型是合适的。

(三)VaR风险测度模型准确性的实证检验

本文运用返回测试中的LR和DQR方法对不同VaR风险测度模型在样本内和样本外的估计准确性和精确性进行检验*Kupiec,P.H.:Techniques for Verifying the Accuracy of Risk Measurement Models,Journal of Derivatives,3(2),1995.*Engle,R.F.and S.Manganelli:CAViaR:Conditional Autoregressive Value at Risk by Regression,Quan Journal of Business and Economic Statistics,22(4),pp.367-381,2004.。为了能使模型的测度能力代表性更具广泛性，选取置信水平α=5%、2.5%、1%、0.5%、0.25%用以评价。表2、表3以及表4分别为样本内和样本外不同模型VaR风险测度能力的检验结果(p-值)。由于本文选择LR和DQR两种方法对风险模型进行检验，为此，在置信水平α下，只有当模型的两种检验结果都超过给定的显著性水平，才认为该模型的VaR测度是可靠有效的，反之，则认为此模型不能成功估计风险损失。若检验结果只能通过LR和DQR方法中的一种，则认为只在该种方法下模型是有效的。本文设定显著性水平为0.05，此外，模型检验p-值越大，则表明模型对VaR风险度量越精确。

表2为样本内GARCH模型在不同分布下的VaR风险测度检验结果，对于其他模型，由于篇幅所限，暂未给出。从中可以看出，在SKST分布下，VaR测度的LR和DQR两种结果在五种多头和空头VaR水平下均能通过检验，而对于正态分布和学生t分布，在不同的VaR水平下有时能同时通过两种检验，有时仅通过其中一种，有时甚至不能通过其中任何一种。此外，在能同时通过LR和DQR两种或一种检验时，SKST分布下的p-值几乎也是最大的。对于其他GARCH族模型在样本内也可得到类似结论，这说明对于同一种GARCH模型，SKST分布下的沪深300指数VaR测度模型更精确可靠。为此，在下文对模型的VaR风险测度能力比较时，只给出分布为有偏学生t分布(SKST)的模型结果。

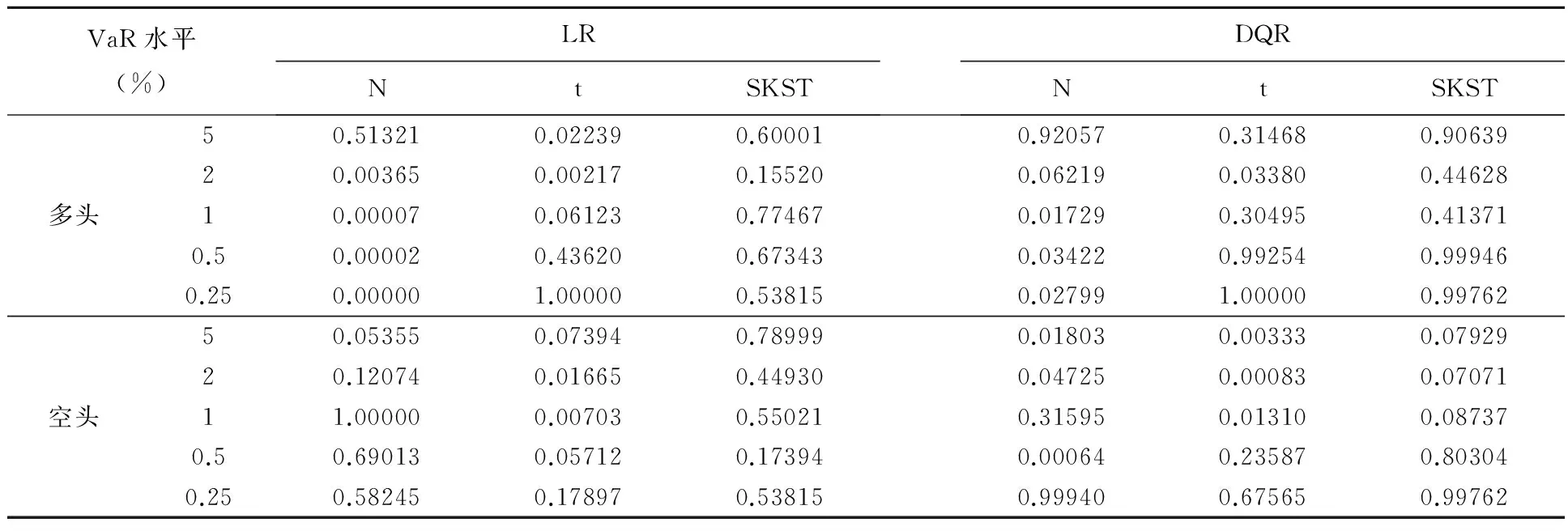
表2 GARCH模型不同分布下的样本内VaR风险测度检验

表3为样本内不同模型在分布SKST下的VaR风险测度能力比较，从中发现，GARCH、GJR、HYGARCH在五种多头和空头VaR水平均能通过LR和DQR检验，而FIGARCH模型在多头VaR水平为5%、0.5%、0.25%以及空头VaR水平2%、1%、0.5%、0.25%下通过检验，说明FIGARCH模型对沪深300指数的VaR风险测度能力不如前三者。进一步从前三个模型通过检验的p-值来看，三个模型各有千秋，有时在某个多头或空头VaR水平下，GARCH的度量能力高些，有时GJR精度高些，有时HYGARCH高些。其中对于空头VaR水平较小(对应于VaR值更大)时，即1%、0.5%、0.25%，HYGARCH模型两种返回检验的p-值均大于GARCH和GJR模型，对于多头的VaR1%、0.5%、0.25%水平，三者的p-值一样，说明HYGARCH模型对沪深300指数空头风险较大时的测度更精确些。

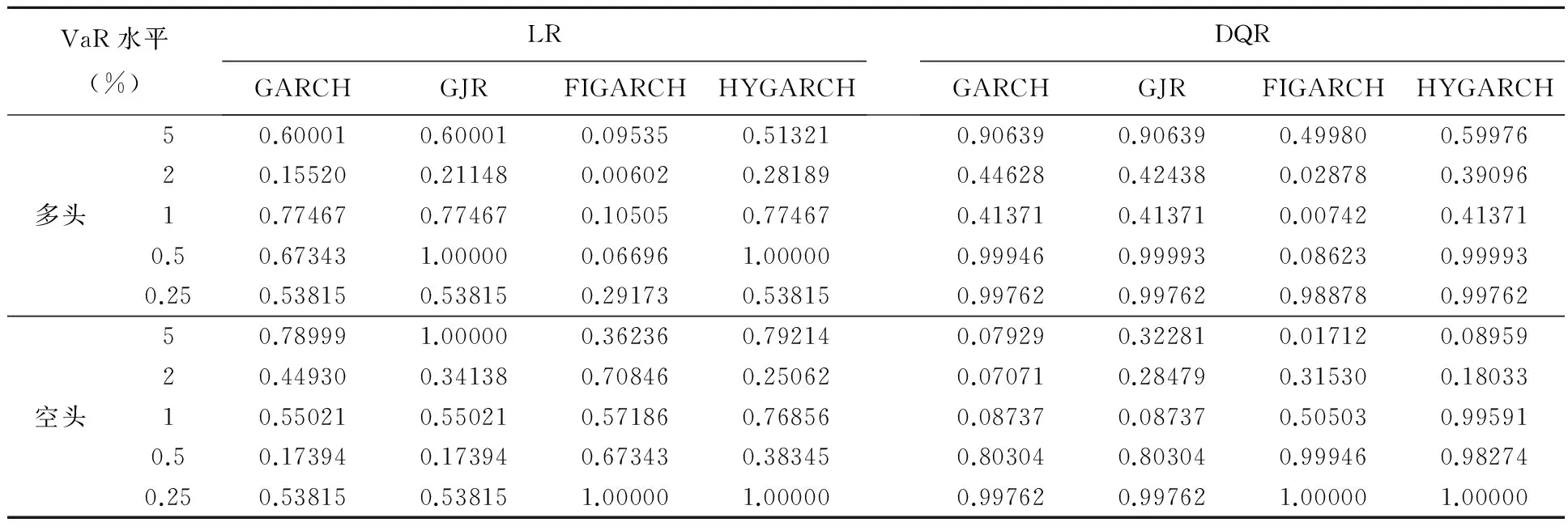
表3 四种GARCH模型SKST分布下的样本内VaR风险测度检验

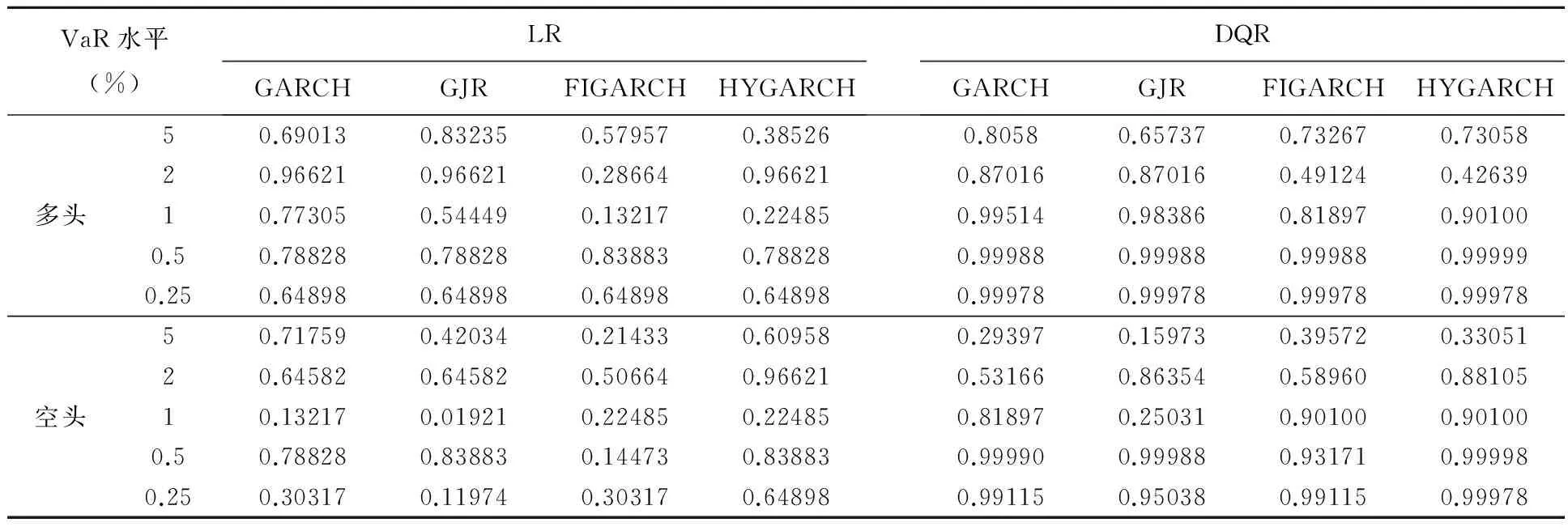
表4 四种GARCH模型SKST分布下的样本外VaR风险测度检验

表4为GARCH、GJR、FIGARCH、HYGARCH模型在SKST分布下样本外VaR测度能力结果。样本内的检验只代表过去的情形，样本外的分析则检验该模型是否适合预测未来风险，因此，它更具有实践意义。从表中可以看出，对于所有的多头和空头VaR水平，四种模型几乎都能通过LR和DQR两种检验，只有GJR在空头VaR水平1%时候不能通过DQR检验。进一步从通过两种检验的p-值来看，对于所有的多头VaR水平，GARCH、GJR、FIGARCH、HYGARCH四种模型出现交替最大的情形；对于空头VaR水平，除了在VaR水平5%时，HYGARCH模型在LR、DQR检验下分别低于GARCH、FIGARCH模型外，其余空头VaR水平下的HYGARCH模型风险测度能力均高于其他三类模型。因此，从以上分析可以看出，HYGARCH模型可作为沪深300指数动态VaR风险测度模型的首选，GARCH模型次之，FIGARCH再次之，而GJR模型则只能作为最后选择。

四、结 论

本文以中国第一只金融股指期货标的物——沪深300指数为例，首先运用经济物理学方法检验了市场一些特征，在此基础上，运用返回测试中的Kupic LR 检验以及动态分位数回归检验法，比较GARCH、GJR、FIGARCH、HYGARCH模型在不同分布下对沪深300指数样本内和样本外VaR风险测度能力，结论如下：

1.沪深300指数收益分布存在尖峰，厚尾和有偏性。收益率的中心服从平稳Lévy分布，其尾部分布可以用幂律函数近似拟合，正尾和负尾幂律指数分别为2.72和2.08。收益率序列基本不存在长记忆性，而收益波动存在长记忆性。沪深300指数收益存在有偏性，说明以沪深300指数为标的资产(即股指期货)的多头和空头风险在相同市场条件下是有显著差异的。由于正尾和负尾对应于空头和多头较高水平时的VaR，因此正尾和负尾的幂律指数不一致，应引起监管部门的注意，对多头和空头头寸的持仓上限及保证金比例等做出有差异性限制。

2.就分布对VaR测度能力而言，无论在样本内还是在样本外，正态分布和学生t分布不能提供较好的风险测度精度，而能刻画收益率分布特征的有偏和尖峰厚尾性的有偏学生t分布则可以使沪深300指数的VaR估计精度得到显著提升。因此，我国监管部门在对市场风险估计时，应尽量根据市场收益分布特征来构建风险模型，以得到更精确的风险测度模型。

3.在沪深300研究样本内阶段，GARCH、GJR、HYGARCH在有偏学生t分布下的模型均能有效进行风险VaR度量，三种模型在不同VaR水平下不尽相同，其中HYGARCH模型对空头VaR水平较高时的度量更优些，而FIGARCH模型的VaR风险测度表现差些。在研究样本外，GARCH、GJR、FIGARCH、HYGARCH在有偏学生t分布下模型的VaR风险测度都是可靠的。进一步从通过检验的p-值来看，在多头VaR水平下，GARCH、GJR、FIGARCH、HYGARCH模型交替出现最优，GARCH模型表现较好些；而HYGARCH模型在空头VaR水平下表现的更优些。因此总的来说，无论在样本外或是样本内，HYGARCH有偏学生t分布下的模型对沪深300样本内和样本外的VaR风险测度能力表现都好，能用于风险估计。

4.有偏学生t分布考虑了市场上不对称信息、厚尾效应对建模的影响，HYGARCH模型将市场杠杆效应、长记忆性考虑在内，从实证结果来看，基于有偏学生t分布的HYGARCH模型能将金融风险出现的最大损失更精确度量出来，市场监管者可根据模型度量出的最大损失，制定不同风控策略，以应对未来可能出现的风险灾害，使金融风险损失降到最低。

[责任编辑：王成利]

本文系山东省社会科学规划会计研究专项(项目编号：15CKJJ21)、山东省软科学研究计划(项目编号2015RKB01272，2016RKB01431)、山东省高等学校人文社会科学研究计划(项目编号J13WG05)资助。

刘桂荣(1971-)，女，齐鲁工业大学工商学院讲师，硕士；周伟杰(1983-)，男，通讯作者，淮阴工学院管理工程学院，博士。

F830.91

A

1003-8353(2016)012-0043-08