机械加工表面轮廓分形维数对数小波谱计算方法
张学良 王余松 温淑花 范世荣 陈永会 兰国生
太原科技大学,太原,030024
机械加工表面轮廓分形维数对数小波谱计算方法
张学良 王余松 温淑花 范世荣 陈永会 兰国生
太原科技大学,太原,030024
为了提高接触表面的建模精度,利用小波的多尺度分析能力,对表面轮廓进行多尺度小波分解,提出了计算机械加工表面轮廓分形维数的对数小波谱法以及有效分解尺度概念,并认为轮廓只在有效分解尺度上具有分形特征;通过M-B函数模拟生成不同分形维数、不同采样区间的分形轮廓;应用对数小波谱法计算了模拟轮廓的分形维数,进而与功率谱密度法(PSD法)等5种方法的计算结果进行了分析比较,结果表明:对数小波谱法能很好地处理分形的多尺度特征,并且选用sym4小波时计算精度最高,误差在0.15%以内;最后应用对数小波谱法对一实际机械加工表面轮廓分形维数进行了计算,说明了其实用性。
机械加工表面轮廓;分形维数;小波分解;有效分解尺度;对数小波谱
0 引言
表观上看似光滑平整的机械加工表面经放大后呈现出大小各异、复杂排列的凸峰和凹谷,说明表面形貌实际上是粗糙和不规则的。机械工程中的表面几何形貌对构件接触处的摩擦、磨损、润滑、密封以及接触性能有很大的影响。研究表明[1],机械加工表面和摩擦磨损表面等粗糙表面轮廓具有非平稳性、自相似性和多尺度特性,分形理论是描述这些特征的一种有效途径;然而,分形理论用于描述机械加工表面时需要分形维数与特征长度尺度参数两个表征参数。准确地计算出其分形维数尤为关键,因为分形维数反映了粗糙表面轮廓结构的复杂程度,定性地刻画了高频成分所占比重。分形维数是机械结合面接触刚度[2-4]、阻尼能耗[5-6]等模型中一个主要的参数,接触刚度与表面分形维数间存在非线性关系(分形维数在1.1~1.4之间)或近似线性关系(分形维数在1.4~1.9之间)[7];在实际应用时,对轮廓维数的计算是必不可少的。
国内外已有许多学者进行了分形维数计算的研究,目前,常用的分形维数计算方法有盒维数法、尺码法、均方根法、协方差法、功率谱密度(PSD)法、结构函数法。李成贵等[8-9]对已知分形维数为1.6的W-M函数所生成的轮廓,分别采用功率谱密度法和结构函数法计算其分形维数,计算结果分别为1.65、1.63。王建军等[10]对尺码法、盒维数法、R/S法、结构函数法以及功率谱密度法5种方法的原理进行了阐述并比较了后3种方法对理论维数分别为1.2、1.5、1.8的W-M 函数的计算结果,结果表明,结构函数法的精度最高,功率谱密度法次之,R/S法精度最低且计算量大,其精度随着理论分形维数的减小而大幅降低。葛世荣等[11]比较了尺码法、盒维数法、方差法和结构函数法等方法计算分形维数分别为1.2、1.5、1.8的W-M函数的计算结果,结果表明,尺码法的误差最大,方差法和盒维数法的误差在10%以上,结构函数法的误差较小,计算结果分别为1.164、1.455、1.761。另外,他们还提出了均方根法[12-13],并将均方根法与结构函数法进行了比较,结果表明,两种方法均有较好的效果;对于较小的分形维数,均方根法的计算精度较高,而对于较大的分形维数,结构函数法的计算精度较高。此外,还可以通过表面轮廓的高度标准差σ和斜率标准差σ′组成方程组解出分形参数D和G[3],本文称之为方程组法。
上述各方法中,由Majumdar等[4]提出的结构函数法对分形维数的计算精度最高,已得到了较多的应用,然而,寻求更高精度的计算方法来提高结合面建模精度是非常必要的。小波具有多尺度分析的能力,可用于处理多尺度自相似问题。王安良等[14-15]提出了用小波变换计算粗糙表面分形维数的方法,根据各分解层小波变换系数的一范数与分解层数k间的关系通过最小二乘拟合求出分形维数,对于由W-M函数及M-B函数生成的轮廓,计算误差在4%以内,在分形维数为1.3~1.6时,计算误差在1%以内。杨红平等[1]通过分形轮廓小波分解系数方差与分形维数间的关系求出分形维数,但没有明确给出通用性的小波分解层数。
鉴于此,本文将小波的多尺度分析能力与分形的多尺度自相似特征相结合,先对分形轮廓进行多尺度小波分解,基于对数小波谱,识别出轮廓具有分形特征的小波分解尺度(从对数小波谱上看在一条直线上或接近同一直线),进而评价轮廓的分形特征并计算其分形维数,提出了机械加工表面轮廓分形维数对数小波谱计算方法,并与功率谱密度法、结构函数法、均方根法以及方程组法的计算精度进行对比,最后将其应用于实际机械加工表面轮廓分形维数的计算,说明了其实用性。
1 机械加工表面轮廓分形维数的对数小
波谱计算方法

(1)
式中,2-m为尺度参数;k为平移参数。
任意信号f(t)∈L2(R)(平方可积函数空间)的离散小波级数表示为
(2)
小波分解系数可以表示为
(3)
(4)
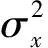
自相似过程具有分形特征,根据文献[17]对自相似的定义f(t)=γ-Hf(γt),分形维数
D=2-H
(5)

(6)
定义1 将序列f(t)的自相关函数定义为
Rf(τ)=E[f(t)f(t-τ)]
(7)
基于多尺度分析的方法,对具有自相似性的粗糙轮廓高度序列进行小波分解,在不同的尺度上,则其小波分解系数满足[18]
(8)
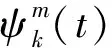
(9)
将式(8)右端利用Parseval定理以及时域卷积定理转化到频域后,式(8)可改写为
(10)
特别地,m=m′,k=k′时,有
(11)

从而有
(12)
式中,var[]为求方差运算。
对式(11)两边取以2为底对数,有
(13)
将式(13)左端记为Ym,得
Ym=lbσ2+mα
(14)
对给定的具有分形特征的实际机械加工表面轮廓进行M层的小波分解,各分解尺度(层)对应的m(m=1,2,…,M)、Ym便是已知的,相应地,对数据点(m,Ym)序列进行直线拟合即可求出直线斜率α,再由前述关系α=2H+1及D=2-H便求出分形维数D,即
D=(5-α)/2
(15)
在此称式(13)或式(14)为对数小波谱。以上分析推理求解机械加工表面轮廓分形维数的方法,本文称之为对数小波谱方法。
2 机械加工表面轮廓分形模拟与分形维数
计算
M-B函数被广泛用于模拟实际机械加工表面轮廓,M-B函数是一个确定性自相似过程,满足Z(x)=γ-(2-D)Z(γx)。其具体表达式为
(16)
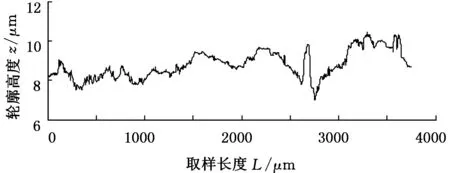
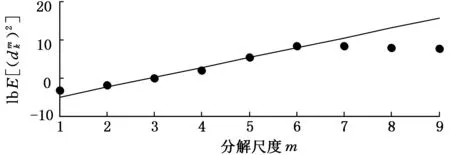
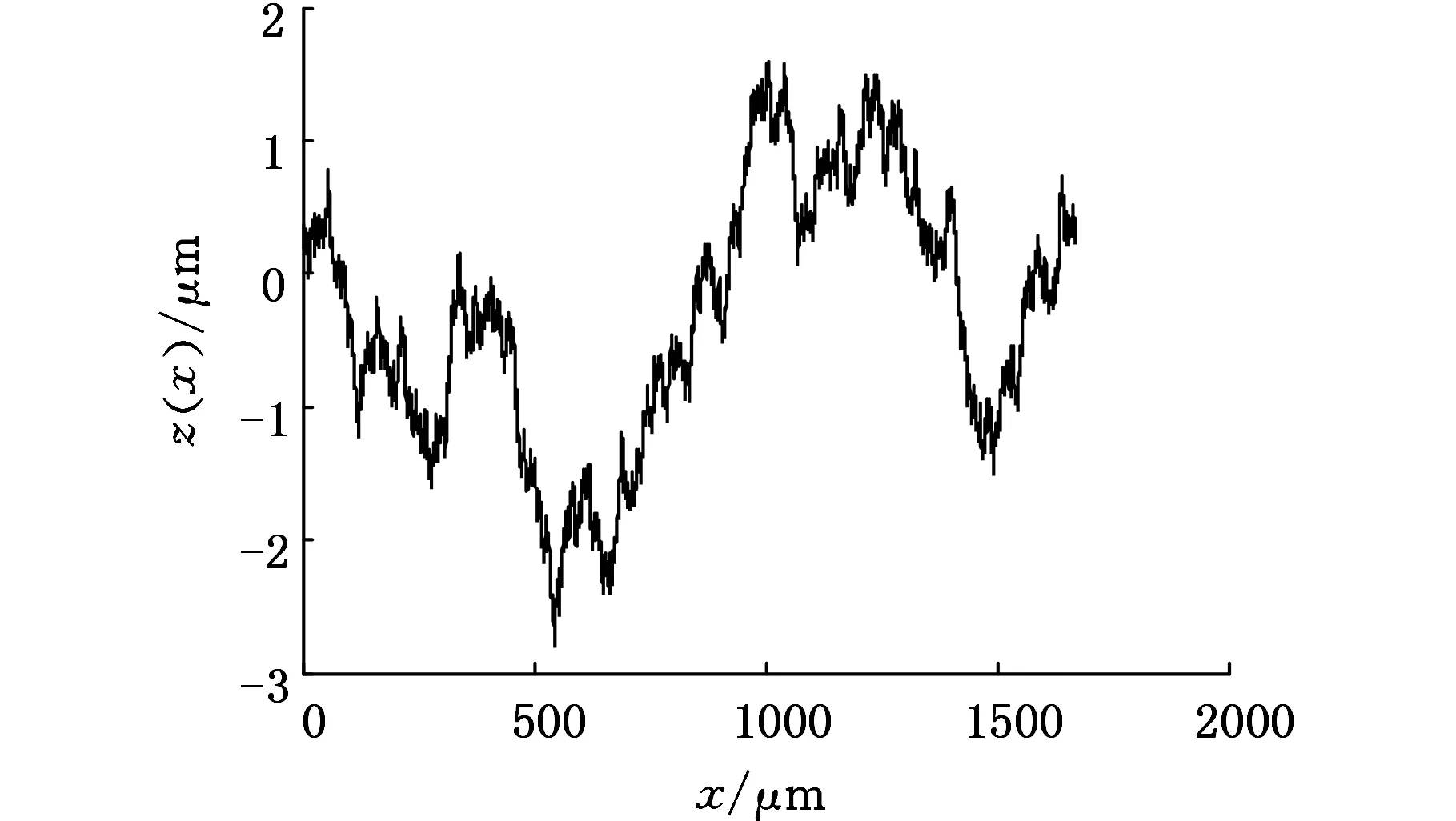
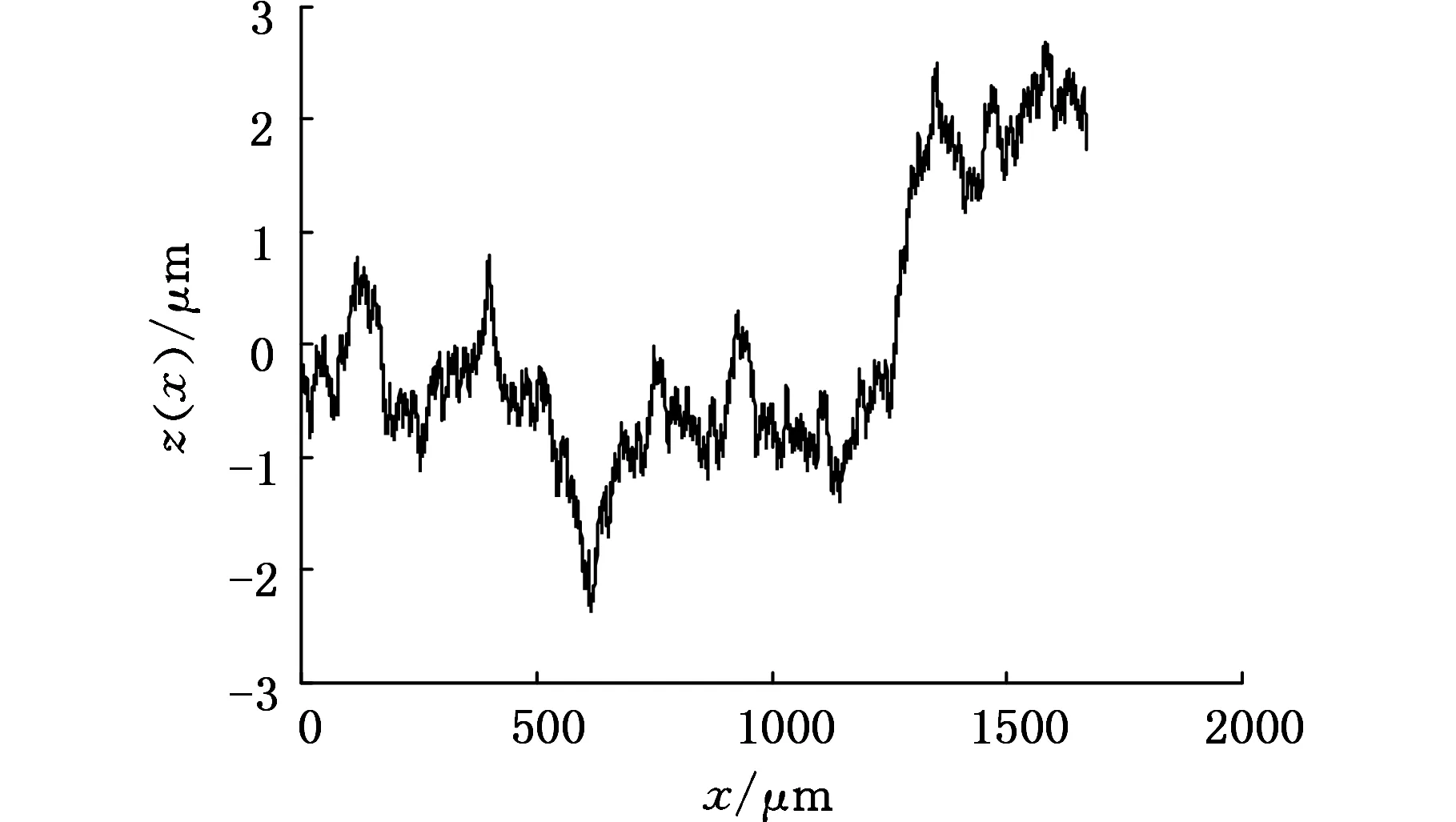
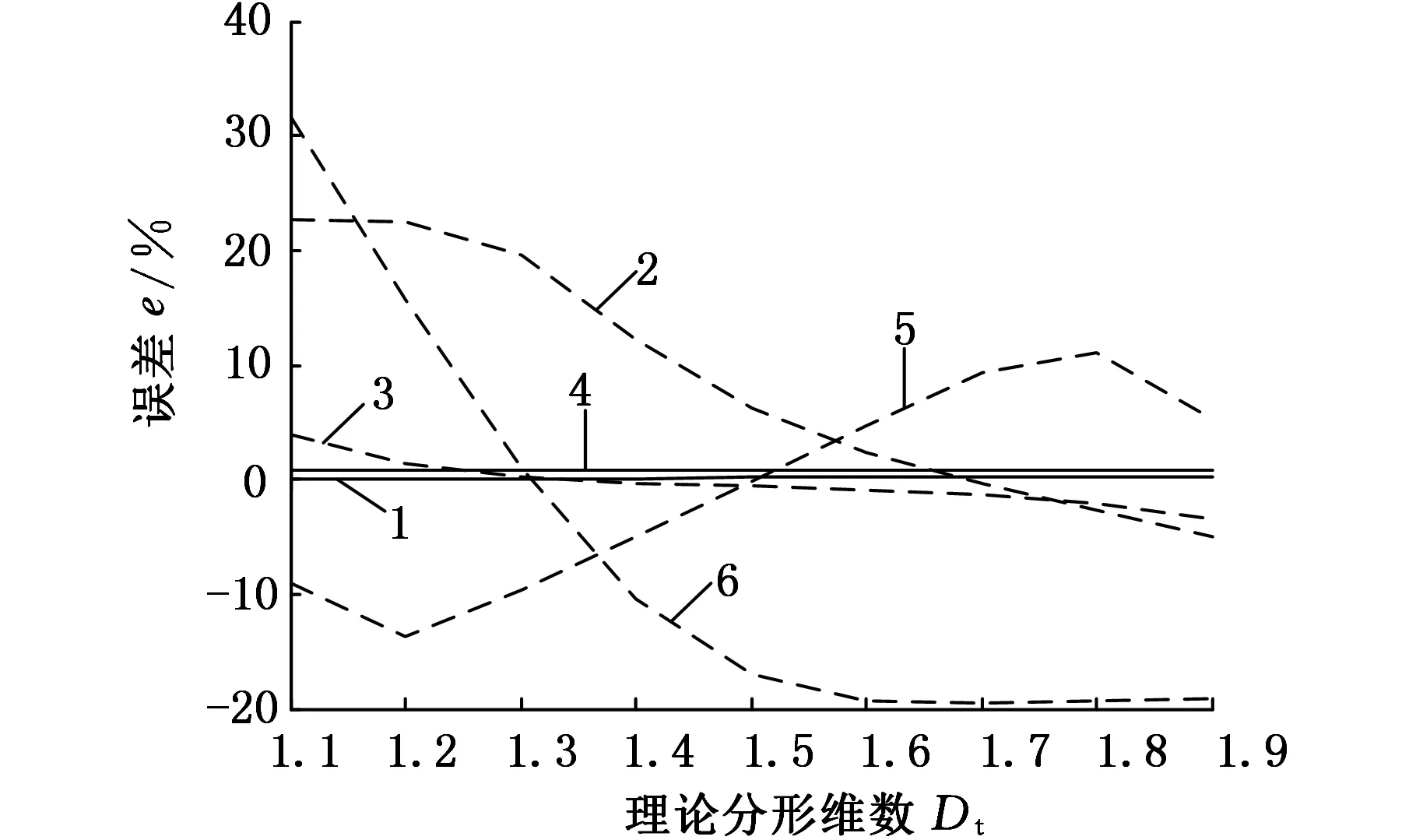
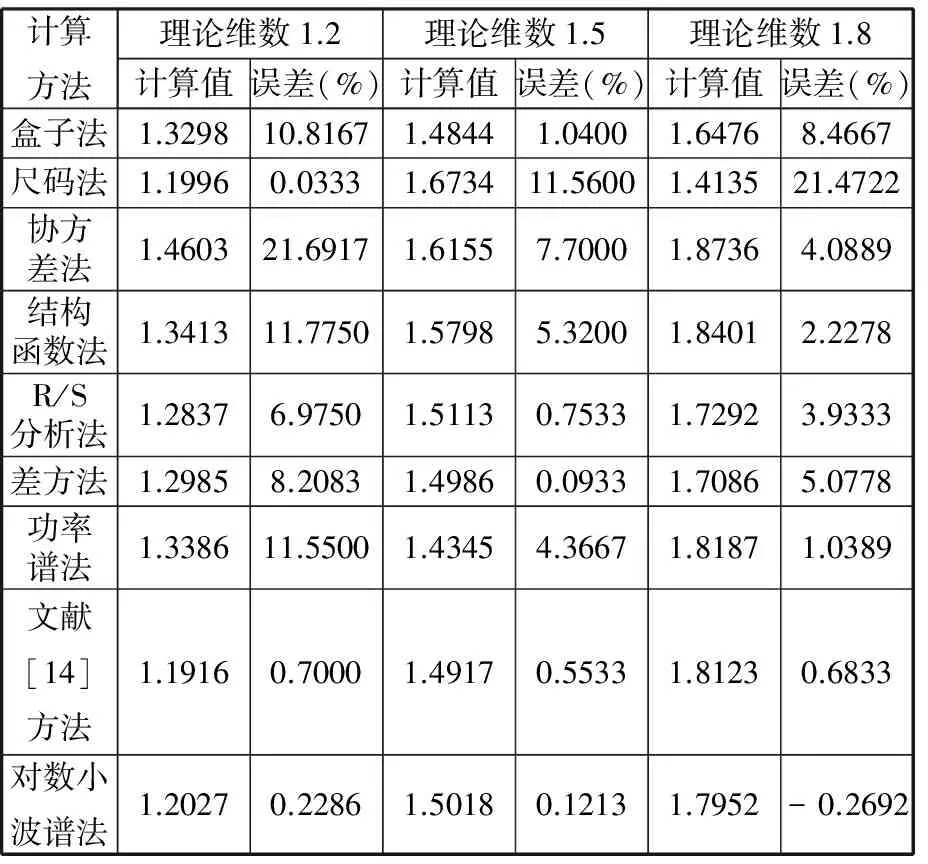
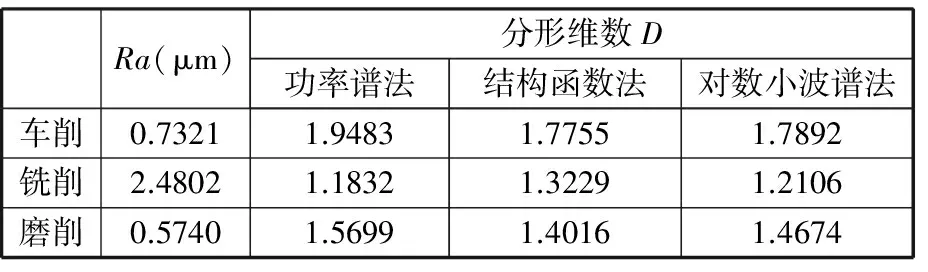
1 式中,z(x)为表面轮廓高度;G为分形特征长度尺度系数;nl为最低频率指数;γnl=1/L;L为采样区间长度。 在实际应用中,最高频率的取值是有限的,即 (17) (a)采样区间(0,L) (b)采样区间(3L,4L) (c)采样区间(10L,11L)图1 理论维数D=1.5时M-B函数生成的不同采样区间的轮廓 在对机械加工表面轮廓进行小波分解时,首先要考虑的是小波基函数的选择和分解尺度(层数)的确定。如何选择小波基函数,目前还没有一个理论标准,大多凭经验。工程中较多采用的小波基函数有db小波、sym小波和haar小波。对于给定长度的序列,最大分解尺度(层数)也是有限制的。从小波理论分析角度来看,最大分解尺度仅由数据长度和小波阶数便可确定,理论上小波分析最大分解尺度M为[20] M=floor[ln(lx/(lw-1))/ln2]= floor[lb(lx/(lw-1))] (18) 式中,floor(·)为向下取整函数;lx为信号长度;lw为滤波器长度,与小波类型有关,对于dbN小波,lw=2N;N为小波函数的消失矩。 本文分别选用db2、sym2、db4、sym4以及haar小波基函数,由式(18)可确定db2与sym2小波对应的最大分解尺度为11,db4与sym4小波对应的最大分解尺度为10,采用haar小波时则为13。根据自相似特征确定具有分形特征的尺 度,对这些尺度进行拟合就可以计算出分形维数。由M-B函数生成理论分形维数Dt为1.1、1.2、…、1.9的模拟轮廊,对上述轮廓在采样区间(3L,4L)上分别进行小波分解,应用本文提出的对数小波谱方法,对具有分形特征的分解尺度进行拟合获得直线斜率α,从而由式(15)计算出相应的分形维数D,结果见表1。 由表1可见,采用sym4小波时计算结果精度最高。图2给出了理论分形维数Dt分别为1.2、1.5、1.8时的对数小波谱及其拟合直线。根据图2,分解尺度m为2、3、4、5、6对应的对数小波谱几乎在一条直线上,其余理论维数类似,轮廓在这几个尺度上(对应轮廓高频部分)具有精确的自相似性,说明轮廓在这几个尺度上具有良好的分形特征(从对数小波谱上看在一条直线上,称之为有效分解尺度),因此分解尺度2、3、4、5、6为有效分解尺度;在尺度大于8(对应轮廓低频成分)时,与小于8的尺度没有严格的相似性,这是因为在生成模拟轮廓时采用的是式(17),而式(17)是有限项级数,存在误差,因此不具有严格的自相似性。对有效分解尺度2~6进行拟合计算的精度很高,误差都在0.15%以内。 表1 各小波计算结果 应用对数小波谱方法,采用sym4小波计算获得的分形维数与应用功率谱密度法、结构函数法、均方根法以及解方程组法获得的结果的比较如图3所示。 (a)Dt=1.2,D=1.2008,误差e=0.063263% (b)Dt=1.5,D=1.502,e=0.13609% (c)Dt=1.8,D=1.8026,e=0.14208%图2 采样区间为(3L,4L)时对数小波谱及其拟合直线 (a)各方法计算分形维数比较 (b)各方法计算误差比较1.对数小波谱方法(sym4小波) 2.均方根法 3.结构函数法 4.文献[1]方法 5.方程组法 6.功率谱密度法 7.分形维数理论值图3 采样区间(3L,4L)上不同计算方法的计算结果 将对数小波谱方法应用到文献[14]中的M-B函数算例,得到的计算结果与文献中其他方法计算结果的比较见表2。由表2可见,对数小波谱方法相对于其他方法有更高的精度。 表2 各方法对文献[14]算例计算结果 图4为由Talysurf5-120轮廓测试仪对车削、铣削和磨削加工表面进行测试获得的表面轮廓曲线,试件材料为45钢,测试的采样间隔为1.25 μm,采样长度为3.75 mm,共有3000个离散采样点。对该轮廓进行db2小波分解,得到图5所示的各加工表面轮廓的对数小波谱,经直线拟合求出其分形维数。分别采用功率谱密度法与结构函数法对上述各轮廓分形维数进行计算,结果如表3所示。 表3 各加工表面轮廓分形维数计算结果 Ra(μm)分形维数D功率谱法结构函数法对数小波谱法车削0.73211.94831.77551.7892铣削2.48021.18321.32291.2106磨削0.57401.56991.40161.4674 (1)提出了一种机械加工表面轮廓分形维数的对数小波谱计算方法以及有效分解尺度的概念。 (a)车削加工 (b)铣削加工 (c)磨削加工图4 各加工表面轮廓 (a)车削加工 (b)铣削加工 (c)磨削加工图5 各加工表面轮廓的对数小波谱 (2)计算轮廓分形维数的关键是选择小波基函数和分解尺度,然而其最大分解尺度可由表面轮廓序列长度和小波阶数确定,可先按最大分解尺度分解。 (3)对数小波谱法能很好地处理分形的多尺度特征,对于由M-B函数模拟的分形轮廓,特别是采用sym4小波时,对数小波谱方法计算误差在0.15%以内,对文献[14]中的算例计算也具有高的准确度。 (4)应用所提出的对数小波谱方法对一车削、铣削和磨削加工表面轮廓分形维数进行了分析计算,表明本文方法具有实用性。 [1] 杨红平,傅卫平,王雯,等.小波系数表征机械加工表面分形特征的计算方法[J].仪器仪表学报, 2010, 31(7):1454-1459. Yang Hongping,Fu Weiping,Wang Wen,et al. Calculation Method for Fractal Characteristics of Machining Topography Surface Based on Wavelet Coefficients[J]. Chinese Journal of Scientific Instrum-ent,2010,31(7):1454-1459. [2] 张学良. 机械结合面动态特性及应用[M]. 北京:中国科学技术出版社, 2002:20-24. [3] 温淑花,张宗阳,张学良,等. 固定结合面刚度分形模型[J]. 农业机械学报,2013,44(2):255-260. Wen Shuhua, Zhang Zongyang, Zhang Xueliang, et al. Stiffness Fractal Model for Fixed Joint Interfaces[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013,44(2):255-260. [4] Majumdar A, Bhushan B. Fractal Model of Elastic-plastic Contact between Rough Surfaces[J]. ASME Journal of Tribology,1991,113(1):1-11. [5] 张学良,王南山,温淑花,等.机械结合面切向接触阻尼能量耗散弹塑性分形模型[J].机械工程学报,2013,49 (12):43-49. Zhang Xueliang,Wang Nanshan,Wen Shuhua, et al. Elastoplastic Fractal Model for Tangential Contact Damping Energy Dissipation of Machine Joint Interfaces [J]. Journal of Mechanical Engineering, 2013,49(12):43-49. [6] 田红亮,郑金华,赵春华,等. 界面损耗因子与法向阻尼的计算方法[J].上海交通大学学报,2015,49(5):687-694. Tian Hongliang, Zheng Jinhua, Zhao Chunhua, et al. Calculating Method of Surface Dissipation Factor and Normal Damping[J]. Journal of Shanghai Jiao Tong University, 2015,49(5):687-694. [7] 张学良,陈永会,温淑花,等.考虑弹塑性变形机制的结合面法向接触刚度建模[J].振动工程学报,2015,28 (1):91-99. Zhang Xueliang, Chen Yonghui, Wen Shuhua, et al. The Model of Normal Contact Stiffness of Joint Interfaces Incorporating Elastoplastic Deformation Mechanism[J]. Journal of Vibration Engineering, 2015,28 (1):91-99. [8] 李成贵,张国雄,袁长良.分形维数与表面粗糙度参数的关系[J].工具技术, 1997, 31(12):36-38. Li Chenggui,Zhang Guoxiong,Yuan Changliang.The Relationship between the Fractal Dimension and Surface Roughness Parameters[J].Tool Engineering,1997,31(12):36-38. [9] 李成贵,刘杰,郎青山.机加工表面轮廓分形维数的两种计算方法[J].航空精密制造技术,1997, 33(4):25-27. Li Chenggui,Liu Jie,Lang Qingshan.Two Methods for the Calculation of the Fractal Dimension of a Machined Surface Profile[J].Aviation Precision Manufacturing Technology,1997,33(4):25-27. [10] 王建军,魏宗信.粗糙表面轮廓分形维数的计算方法[J].工具技术, 2006, 40(8):73-75. Wang Jianjun,Wei Zongxin.Computation Method for Fractal Dimension of Rough Surface Profile[J].Tool Engineering,2006,40(8):73-75. [11] 葛世荣,索双富.表面轮廓分形维数计算方法的研究[J].摩擦学学报, 1997, 17(4):354-362. Ge Shirong,Suo Shuangfu.The Computation Methods for the Fractal Dimension of Surface Profiles[J].Tribology,1997,17(4):354-362. [12] 葛世荣, Tonder K. 粗糙表面的分形特征与分形表达研究[J].摩擦学学报, 1997, 17(1):73-80. Ge Shirong,Tonder K.The Fractal Behavior and Fractal Characterization of Rough Surfaces[J]. Tribology,1997,17(1):73-80. [13] 朱华,葛世荣.结构函数与均方根分形表征效果的比较[J].中国矿业大学学报, 2004, 33(4):396-399. Zhu Hua,Ge Shirong.Comparison of Fractal Characterization Effects of Structure Function and Mean Square Root[J].Journal of China University of Mining & Technology,2004,33(4):396-399. [14] 王安良,杨春信. 机械加工表面形貌分形特征的计算方法[J].中国机械工程, 2002, 13(8):714-718. Wang Anliang,Yang Chunxin.The Calculate Method for the Fractal Characterization of Profiles[J].China Mechanical Engineering,2002, 13(8):714-718. [15] 王安良,杨春信.小波变换方法评价曲线的分形特征[J].机械工程学报, 2002, 38(5):80-85. Wang Anliang,Yang Chunxin.Wavelet Transform Method Evaluate the Fractal Characterization of Profiles[J]. Chinese Journal of Mechanical Engineering,2002,38(5):80-85. [16] Flandrin P. On the Spectrum of Fractional Brown-ian motions [J]. IEEE Transactions on Informa-tion Theory,1989,35(1):197-199. [17] 杨福生.小波变换的工程分析与应用[M].北京:科学出版社, 1999. [18] Wornell W. Wavelet-Based Representations for the 1/f Family of Fractal Processes [J]. Proceedings of the IEEE,1993,81(10):1428-1450. [19] Jackson R L, Streator J L. A Multi-scale Model for Contact between Rough Surfaces[J]. Wear, 2006, 261:1337-1347. [20] 樊计昌,刘明军,王夫运,等.浅析小波最大分解层[J].科技导报(北京), 2008, 26(10):40-42. Fan Jichang,Liu Mingjun,Wang Fuyun,et al. Analysis on Maximum Wavelet Decomposition Level from Theory and Application[J].Science & Technology Review(Beijing),2008,26(10):40-42. [21] Majumdar A, Tien C L. Fractal Characterization and Simulation of Rough Surfaces[J]. Wear, 1990, 136 (2):313-327. (编辑 苏卫国) Logarithmic Wavelet Spectrum Method for Computing Fractal Dimension of Machined Surface Profiles Zhang Xueliang Wang Yusong Wen Shuhua Fan Shirong Chen Yonghui Lan Guosheng Taiyuan University of Science and Technology, Taiyuan, 030024 A multi-scale wavelet decomposition for surface profiles was achieved herein by the multi-scale analysis capability of wavelet; and a logarithmic wavelet spectrum method for calculating the fractal dimensions of machined surface profiles and the effective decomposition scale concept were proposed. Fractal profiles with different fractal dimensions and different sampling intervals were generated by M-B function. The fractal dimensions of simulated profiles whose dimensions were known were calculated by logarithmic wavelet spectrum method, which was compared with the calculation results of other five kinds of methods such as the power spectral density (PSD) method. The results show that logarithmic wavelet spectrum method may process multi-scale fractal features nicely, and it has the highest accuracy with errors less than 0.15% when sym4 wavelet is adopted. Finally, logarithmic wavelet spectrum method was applied to calculate the fractal dimensions of actual machined surface profiles and the results illustrate its practicability. machined surface profile; fractal dimension; wavelet decomposition; effective decomposition level; logarithmic wavelet spectrum 2016-01-19 国家自然科学基金资助项目(51275328);山西省自然科学基金资助项目(201601D011062) TH161.14 10.3969/j.issn.1004-132X.2016.23.004 张学良,男,1964年生。太原科技大学机械工程学院教授、博士研究生导师。研究方向为机械结构动态特性、现代优化设计理论与方法、现代制造技术。王余松,男,1991年生。太原科技大学机械工程学院硕士研究生。温淑花(通信作者),女,1963年生。太原科技大学机械工程学院教授。范世荣,男,1990年生。太原科技大学机械工程学院硕士研究生。陈永会,男,1975年生。太原科技大学机械工程学院副教授。兰国生,男,1975年生。太原科技大学机械工程学院副教授。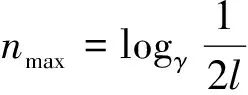






3 计算实例
4 结论