基于IEGF-AHP算法的机床精度评价
要小鹏 黄华川 殷国富 李光明
1.西南科技大学,绵阳,621010 2.四川大学,成都,610065
基于IEGF-AHP算法的机床精度评价
要小鹏1黄华川1殷国富2李光明1
1.西南科技大学,绵阳,621010 2.四川大学,成都,610065
针对数控机床精度评价过程中定性指标不清晰、量化指标不准确等缺点,提出了一种基于区间可拓灰色模糊算法的机床精度评价方法。该方法通过建立机床各评价指标的可拓判断矩阵,求取相应的权重系数,利用灰色模糊综合评价法进行逐次分析,获得综合评价值。以VXC-960型机床为例,对不同时间段的机床精度进行反复检测与评价,以获取机床精度的演化规律与主要影响因素,提出相应的应对措施。实验结果证明了该方法的有效性和可行性。
数控机床;区间可拓;灰色模糊分析法;精度综合评价
0 引言
数控机床整机精度是衡量机床产品质量的重要依据,主要包括机床静态精度、准静态精度和动态精度[1-2]。随着系统工程理论在机械行业的大量运用,多指标综合评价方法在机床精度评价方面的优势已初步显现[3]。刘世豪等[4]运用模糊综合评判法对数控机床综合性能进行评价研究并取得了良好的效果。韩英强等[5]提出了一种基于模糊群组层次分析法的指标体系综合评价方法,并通过实例进行了验证。根据上述文献资料,数控机床精度评价应综合考虑不同的评价因素,选用相应的评价方法,将多个评价因素或评价指标转化成能反映评价对象总体性能特征的信息。针对传统的评价分析法在构建评价判断矩阵和确定评价因素权重系数中存在评价矩阵柔性差、随机性偏差较大等缺点[6],本文提出了一种区间可拓灰色模糊层次分析(intervalextensiongreyfuzzyanalytichierarchyprocess,IEGF-AHP)算法。该方法采用区间域集合来构造判断矩阵,降低了采用单个点值构建判断矩阵的盲目性,同时考虑了判断值的模糊性和多指标评价值的经验性,使判断矩阵能包含多种因素,更加合理。笔者选取一台VXC-960型三轴数控机床进行误差补偿,以机床用户评判为主对该机床的整机精度进行全面综合评价。
1 区间可拓层次分析法
1.1 构建区间可拓判断矩阵
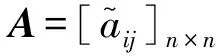
1.2 求解判断矩阵的权重系数
对1.1节建立的区间可拓判断矩阵,按如下方法求取符合一致性验证的权重系数[8]:
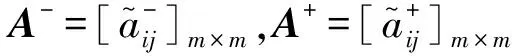
(2)根据A-、A+,求解判断因子u和v的值:
(1)
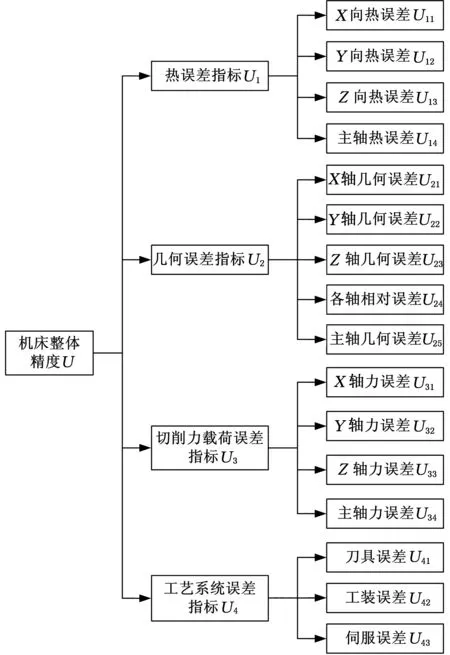
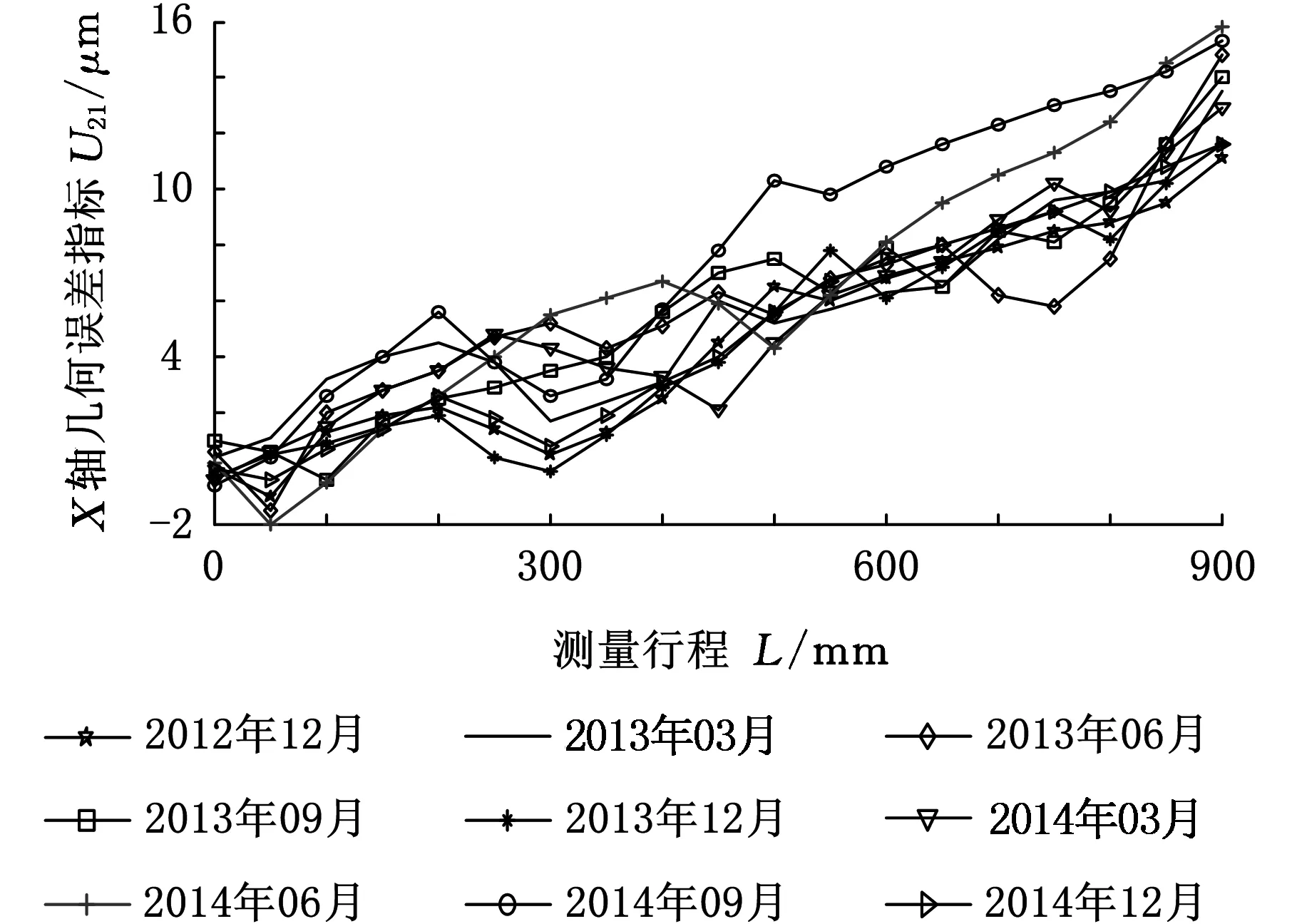
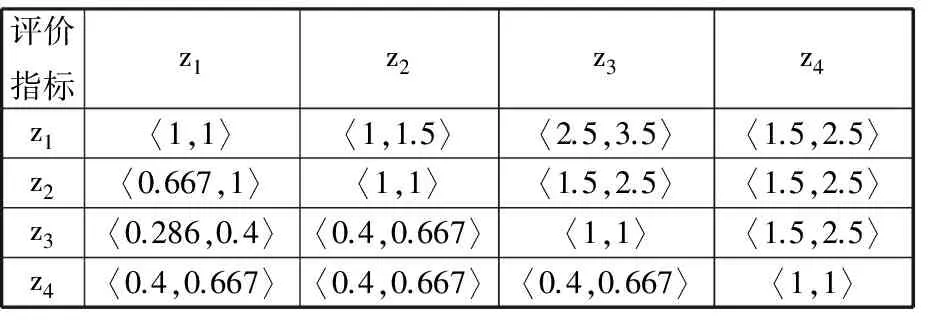
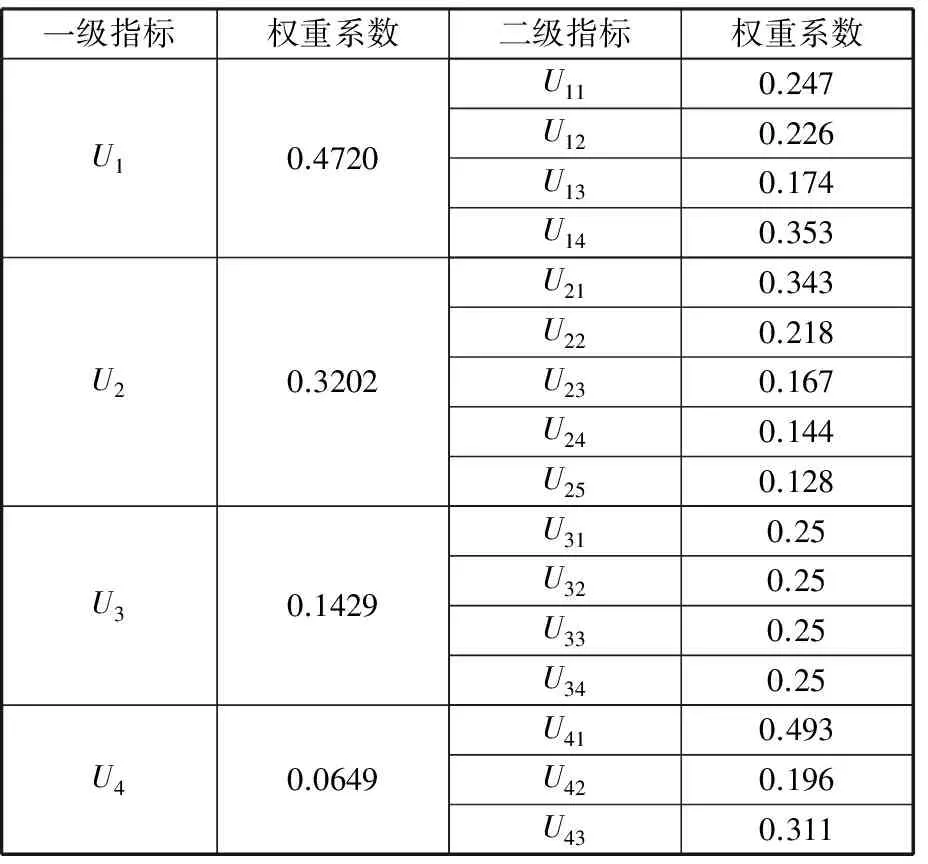
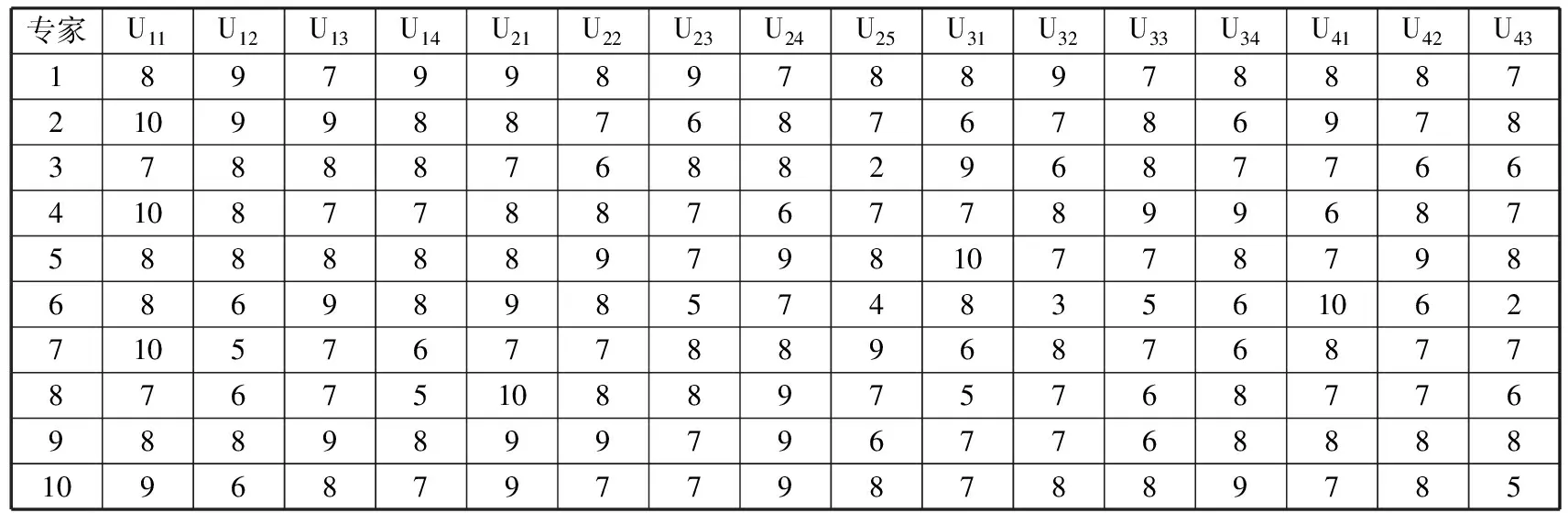
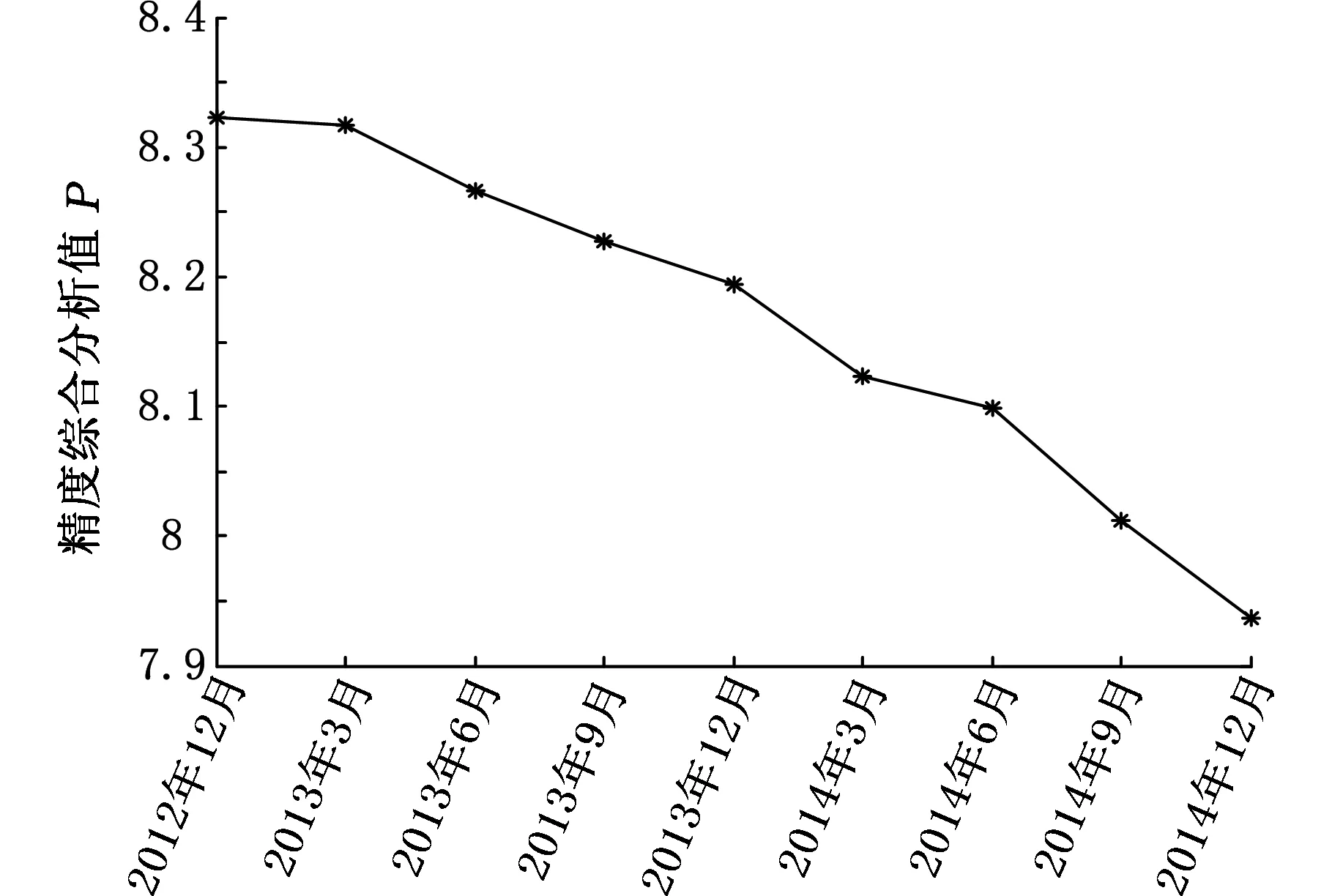
其中,判断因子u、v分别为符合条件0 (3)一般情况下,0≤u≤1≤v表明判断矩阵具有可拓性以及较好的一致性。 (4)求解权重向量,通过步骤(2)、(3)计算u、v,由此获得满足判断矩阵一致性条件的可拓区间数权重: Q=(Q1,Q2,…,Qn)=〈ua-,va+〉 (2) 式中,Qn为u层中第n个因素对u-1层中某项因素的可拓区间权重值。 1.3 任意层次排序 (3) 2.1 单因素集模糊评价 单因素集模糊评价步骤如下[9]: (1)确定评价指标集U={u1,u2,…,un}。 (2)确定评价因素集V={v1,v2,…,vm},请行业专家对机床各层次指标,按相关评分标准进行打分,评分范围为0~10,评价集区间0~2、2~4、4~6、6~8、8~10分别表示很差、较差、一般、较好、很好。 (3)确定灰色评价系数与评价矩阵。确定评价灰类的本质是根据专家对评价集打分并进行灰类白化处理,通过定量计算完成定性分析。根据灰色系统,将其白化权函数分为上类形态灰数、中类形态灰数和下类形态灰数[10]。 上类形态灰数,即⊗∈[c1,∞],定义如下: (4) 中类形态灰数,即⊗∈[0,2c1,2c2],定义如下: (5) 下类形态灰数,即⊗∈[0,c1,c2],定义如下: (6) 式中,c1、c2为白化权函数的阈值。 则可得灰色统计数和总灰色统计数: (7) (8) 由此可获取m位专家对第q个评价因素第j个评价级别的灰色权值lij=nij/n。由lij构成的灰色模糊评价矩阵为 Lij=[lij]m×n (9) 因此,综合单因素权重矢量Y和灰色模糊评判矩阵Lij,按照M(,+)模型进行合成运算,则单因素的模糊综合评价模型为[11] N=YLij (10) 式中,N为单因素模糊综合评价结果。 2.2 多因素多层次集模糊评价 在式(10)的基础上,综合第i个因素的权重矢量Yi进行合成运算,则第i个因素的模糊综合评价模型为 Ni=YiN (11) 根据2.1节、2.2节所述两种情况下的评价结果,利用分值最大原则[12],选取评价标准等级并对应相应分值,如S=(2,4,6,8,10),则各级指标的机床精度综合评价值为 P=Ni·S (12) 3.1 机床精度评价体系的构建 影响机床精度的因素很多,因此需要建立一个多层次的评价体系。为降低评价风险,精度评价因素指标选择依据以下原则:①所选择的评价指标应尽可能全面;②应尽可能选择那些容易获取数据的指标项;③所选取的指标尽可能参考机床精度检测标准,并多方咨询专家和技术人员的意见。 本文利用层次分析(analytichierarchyprocess,AHP)法思想建立图1所示的评价指标框架,数控机床精度整体评价体系分2个层次,第一层为总目标因素集U={U1,U2,U3,U4};第二层为下一级目标因素集Ui(i=1,2,3,4),其中,U1={U11,U12,U13,U14},U2={U21,U22,U23,U24,U25},U3={U31,U32,U33,U34},U4={U41,U42,U43}。 图1 数控机床精度指标评价体系 3.2 机床误差测量与精度分析 机床误差测量必须严格遵守ISO230机床标准规范,根据3.1节提出的机床精度指标进行检测。由于篇幅关系,本文仅列举X轴几何误差U21的变化情况,如图2所示。 图2 数控机床精度指标 传统评价集为{不合格,合格},根据机床误差测量结果评价机床精度是否合格。由图2可知,24个月内(每隔3个月测量一次)机床X轴几何误差指标均小于20μm且保持较为稳定的状态,根据机床精度检测规范可认定该机床X轴几何精度合格。这种传统方法只能对机床精度进行定性分析,而无法进行定量评价,同时也无法对机床精度的稳定性状态作出更加合理的预测和评价。 3.3 确定评价因素集权重 对数控机床整体精度进行灰色模糊综合评价时,各因素集指标的权重系数对总体评判结果会产生较大的影响。由于不同的权重系数会直接影响评判结果,因此如何正确地确定权重系数尤为重要。本文采用AHP方法来确定各因素集指标的权重系数,运用该方法对每层中各项子因素集进行两两比较,确定矩阵中各元素的值,建立评价指标重要度矩阵。通过选取合适的评价标度,将体现定性判断的特征性用数值定量的方式进行描述,获得评价判断矩阵。根据AHP法的定义,对一组因素指标的重要性进行量化比较。为了提高决策判断的准确性,将各项机床精度评价指标的相对重要性关系进行量化,如表1所示。根据1.2节给出的算法建立区间可拓评级矩阵,通过表1可得: 表1 精度指标重要性列表 注:z1表示热误差,z2表示几何误差,z3表示切削力载荷误差,z4表示系统误差。 按照上述方法类推,对图1中的各级指标进行分层评价,建立每层重要度的判断矩阵,然后计算各级评价指标的权重系数,如表2所示。 表2 精度指标权重系数表 一级指标权重系数二级指标权重系数U10.4720U110.247U120.226U130.174U140.353U20.3202U210.343U220.218U230.167U240.144U250.128U30.1429U310.25U320.25U330.25U340.25U40.0649U410.493U420.196U430.311 3.4 机床精度模糊评价 3.4.1 评价因素集样本矩阵 评价因素集是行业专家根据机床的工作状态,对相关各项机床精度指标进行客观打分而产生的评价表。对于不同评价指标,其评语等级所代表的含义各不相同,根据数控机床各项精度指标的特点,给出数控机床精度指标的评价集S={s1,s2,s3,s4,s5},其中,s1表示很差,s2表示较差,s3表示一般,s4表示较好,s5表示很好。 通过专家和相关工程人员对各层精度指标进行评价后,对评价的结果进行统计和整理得到各层的评价矩阵。考虑到每次评价都需要根据评价人员的评判结果建立因素评价矩阵,因此本文在设计机床精度测评系统时,对底层精度指标设置分段区间进行分类,区间0~2、2~4、4~6、6~8、8~10分别表示很差、较差、一般、较好、很好,共设5个评价等级,即S={2,4,6,8,10}。根据图1构建的精度评价指标体系聘请10位行业内专家,选取2012年第4季度的机床误差测量数据作为相关因素评价指标进行重要度评分,建立评语集,如表3所示。 3.4.2 确定灰色系数与评价模糊权矩阵 根据式(4)~式(6),将各自评价灰类转化成对应的白化函数,以表3中二级精度指标U11的专家打分为例,由式(7)、式(8)计算属于各评价标准的灰色系数:n11=9.111,n12=7.857,n13=3,n14=n15=0。则二级指标U11的总灰色系数n1=n11+n12+n13+n14+n15=19.968。同理,可得U12、U13、U14的总灰色系数n2=23.130,n3=21.692,n4=22.327。通过n1和二级指标U11的灰色系数n1j(j=1,2,3,4),作归一化处理可得到机床评价二级指标U11的灰色权向量r1=(r11,r12,r13,r14,r15)=(0.4562,0.3934,0.1502,0,0)。采用上述算法同理可求得r2=(0.3507,0.4015,0.2335,0.0144,0),r3=(0.4047,0.4017,0.1936,0,0),r4=(0.3683,0.3839,0.2329,0.0149,0)。根据式(9)构成单因素灰色模糊权矩阵L21,以此类推可获得其他3个单因素灰色模糊权矩阵L22、L23、L24: 表3 二级精度指标专家评价表 3.5 机床精度综合评价结果 对二级指标评价模型而言,首先利用第二层的指标权重系数与相应的评判矩阵计算本层各指标的评判结果。将该层评判结果作为第一层指标的评判矩阵,然后利用该评判矩阵乘以相应的指标权重系数得到第一层的综合评判结果。 根据式(9),求出一级指标的模糊评价向量: B1=Y21L21=(0.3924,0.3933,0.2058,0.0085,0) B2=Y22L22=(0.4057,0.3838,0.2001,0.0102,0) B3=Y23L23=(0.3589,0.3830,0.2395,0.0185,0) B4=Y24L24=(0.3624,0.3904,0.2333,0.0139,0) 根据最大隶属度原则分析灰色模糊综合评判结果,若评判结果向量B中至少出现2个相等的最大分量,则模糊综合评判结果无效,否则评判结果是合理可行的。通过对比分析发现模糊评价向量B、B1、B2、B3、B4中都没有出现相同的最大值, 因此基于最大隶属度原则可知评判结果是有效的。根据式(10)求出评价对象的模糊评价向量: 由式(11)求取机床精度评价的整体得分: P=N·S=(0.3899,0.3886,0.2106,0.0108,0)· (10,8,6,4,2)=8.315 通过上述计算可得,该型机床的精度综合分析值为8.315,属于“很好”,与传统方法评价所得结果“合格”比较,该方法的评价结果更加直观有效。 基于J2EE开发平台,利用上述算法进行机床整机精度评价软件设计。为了验证机床补偿后精度状态的稳定性,每隔3个月对机床各项精度进行一次检测并打分,共持续2年,将每次打分结果输入评价软件计算机床整机精度得分,精度演化规律如图3所示。从图3所示结果可以看出,近2年内,机床总体精度呈衰退趋势,说明该机床主要运动部件磨损较为严重,采用软件补偿能在短期内保持其精度稳定性。在满足加工精度的前提下,需要按期根据机床精度状态调整补偿算法的参数和阈值。同时发现,每年中第4季度和第二年1季度相对第二年第2、3季度的机床精度变化趋势要略低一些,说明环境温度的变化对机床精度有一定的影响,因此在完善机床误差系统的时候需要考虑增加环境温度补偿单元。另外,机床精度的综合评分相对精密加工仍然偏低,其主要原因是没有对机床切削力载荷变形误差和加工工艺系统误差进行系统补偿,因此进一步提高机床的综合精度需要从上述两个误差指标入手。 图3 机床整机精度演化规律 (1)在现有层次分析法的基础上,结合可拓学理论、灰色理论、模糊理论,提出了一种区间可拓的灰色模糊评价模型与分析方法。该方法增强了评价模型的柔性,能有效避免运用传统分析方法在构造判断矩阵中由于各位专家评判侧重点和观点不同,导致判断矩阵一致性较差的问题,同时有效降低了构建判断矩阵的重复计算量。 (2)通过对机床热误差、几何误差、切削力载荷误差、加工工艺系统误差及其16个二级指标进行分析评价,建立了机床整体精度的评价体系和评价结构拓扑关系。首先采用专家打分的方法建立各层次的区间可拓的判断矩阵,然后计算各指标项的隶属度,最后采用灰色模糊评价算法对机床整体精度进行评价。 (3)实例评价说明,机床的精度综合分析值为8.315,属于“很好”,说明通过补偿后,机床精度有了很大的提高,与实际情况相符合,从而证明了区间可拓的灰色模糊评价模型与分析方法的可行性和有效性。 (4)机床精度的综合评分相对精密加工仍然偏低,其主要原因是没有对机床切削力载荷变形误差和加工工艺系统误差进行系统补偿,因此进一步提高机床的综合精度需要从上述两个误差指标入手。由此可见该评价方法能快速、客观、全面地对机床精度作出合理的评价。 [1] 要小鹏,殷国富,李光明.数控机床进给轴综合误差解耦建模与补偿研究[J].机械工程学报,2016,52(1):184-192.YaoXiaopeng,YinGuofu,LiGuangming.PositioningErrorofFeedAxisDecouple-separatingModelingandCompensatingResearchforCNCMachineTools[J].JournalofMechanicalEngineering, 2016, 52(1): 184-192. [2] 要小鹏,殷国富,方辉,等. 五轴机床误差建模与补偿解析新算法研究[J]. 四川大学学报(工程科学版), 2013, 21(5):1084-1089.YaoXiaopeng,YinGuofu,FangHui,etal.ANewSynthesisErrorModelingandCompensatingAlgorithmoftheFive-axisMachineTools[J].JournalofSichuanUniversity(EngineeringScienceEdition), 2013,21(5):1084-1089. [3] 仇健.GMC2550u桥式加工中心样机综合精度测评研究[J].机械工程学报,2014,50(1):137-151.QiuJian.StudyonTestingandEvaluationofComprehensiveAccuracyofGMC2550uPrototypeBridge-typeMachiningCentre[J].JournalofMechanicalEngineering, 2014,50(1):137-151. [4] 刘世豪, 叶文华, 唐敦兵,等. 基于层次分析法的数控机床性能模糊综合评判[J]. 山东大学学报(工学版),2010, 40(1): 68-72.LiuShihao,YeWenhua,TangDunbing,etal.Fuz-zyComprehensiveEvaluationforthePerformanceofaNumericalControlMachineToolBasedontheAnalyticHierarchyProcess[J].JournalofShandongUniversity(EngineeringScience), 2010, 40(1): 68-72. [5] 韩英强, 吴晓平, 王甲生. 一种基于模糊群组AHP的指标体系评价方法[J]. 舰船电子工程, 2013, 33(1): 34-36.HanYingqiang,WuXiaoping,WangJiasheng.IndicatorSystemComprehensiveEvaluationBasedonFuzzyGroupAHP[J].ShipElectronicEngineering, 2013, 33(1): 34-36. [6] 王桂萍,贾亚洲,周广文. 基于模糊可拓层次分析法的数控机床绿色度评价方法及应用 [J].机械工程学报, 2010, 45(3):141-147.WangGuiping,JiaYazhou,ZhouGuangwen.EvaluationMethodandApplicationofCNCMachineTool’sGreenDegreeBasedonFuzzy-EAHP[J].JournalofMechanicalEngineering, 2010, 45(3):141-147. [7]SaatyTL.TheAnalyticHierarchyProcess[M].NewYork:McGraw-Hill,1980. [8] 郝庆波,杨兆军,陈传海,等. 基于区间层次分析法的数控机床可靠性预计[J].吉林大学学报(工学版), 2012, 42(7):845-850.HaoQingbo,YangZhaojun,ChenChuanhai,etal.ReliabilityPredictionforNCMachineToolBasedonIntervalAHP[J].JournalofJilinUniversity(EngineeringandTechnologyEdition), 2012, 42(7):845-850. [9] 张翠英, 张静. 灰色模糊评价法在竞争情报系统绩效评价中的应用[J].情报科学, 2010, 28(1):81-85.ZhangCuiying,ZhangJing.GreyandFuzzyEvaluationintheUseofComprehensiveEvaluationofCompetitiveIntelligenceSystem[J].InformationScience, 2010, 28(1): 81-85. [10]ChiouHK,TzengGH.FuzzyHierarchicalEvaluationwithFuzzyEvaluation[J].InternationalJournalofFuzzySystems, 2001, 3(3): 466-474. [11]NachiappanSubramanian,RamakrishnanRamanathan.AReviewofApplicationsofAnalyticHierarchyProcessinOperationsManagement[J].Int.J.ProductionEconomics, 2012,138 (2):215-241. (编辑 张 洋) AccuracyEvaluationofCNCMachinesBasedonIEGF-AHPAlgorithm YaoXiaopeng1HuangHuachuan1YinGuofu2LiGuangming1 1.SouthwestUniversityofScienceandTechnology,Mianyang,Sichuan,621010 2.SichuanUniversity,Chengdu,610065 AccordingtothedisadvantagesofindexeswerefuzzyandinaccurateduringCNCmachineevaluation,anewevaluationmethodofCNCaccuracywasputforwardbyintervalextensiongreyfuzzyanalyticalgorithm.Thismethodbuiltintervaljudgmentextensionmatrixandcalculatedthecorrespondingweightcoefficients.Thecomprehensiveevaluationvalueswererequiredbygreyfuzzyevaluationmethod.ThoughdetectingandevaluationsrepeatedlyatdifferentperiodsonVXC-960typemachine,evolutionlawsofmachinetool’saccuracyandmainfactorsofaffectingcurrentaccuracywereacquired,andthecorrespondingcountermeasureswereputforward.Experimentalresultsshowthattheevaluationmethodhashigheffectivenessandfeasibility. CNCmachine;intervalextension;greyfuzzyanalyticmethod;accuracycomprehensiveevaluation 2015-09-22 国家自然科学基金资助项目(11176027);科技部重大仪器设备专项基金资助项目(2012YQ130226);四川省科学研究计划资助项目(2015ZR0018);四川省教育厅资助项目(16ZA0135,07zd1004);西南科技大学博士基金资助项目(14zx7163) TH161 10.3969/j.issn.1004-132X.2016.23.015 要小鹏,男,1979年生。西南科技大学制造科学与工程学院讲师。主要研究方向为机床误差建模与补偿。发表论文10余篇。黄华川,男,1976年生。西南科技大学制造科学与工程学院讲师。殷国富,男,1956年生。四川大学制造科学与工程学院教授、博士研究生导师。李光明,男,1976年生。西南科技大学制造科学与工程学院讲师。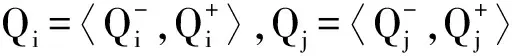
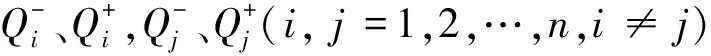
2 灰色模糊评价算法
3 数控机床精度评价实例
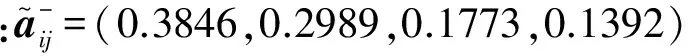
4 数控机床精度评价分析
5 结论

