离合器操纵机构扭转弹簧参数优化

朱文博 赵熙熙 甘 屹 陈 龙

上海理工大学，上海，200093



离合器操纵机构扭转弹簧参数优化

朱文博 赵熙熙 甘 屹 陈 龙

上海理工大学，上海，200093

为了评估某品牌汽车离合器性能，构建了离合器系统台架测试平台，通过模拟离合器系统在整车上的安装状态进行测试，得到踏板特性曲线及相关试验数据。针对台架测试中出现最大踏板力过大、预紧力过小、踏板下降力过小等问题，对离合器操纵机构进行力学建模，并分析影响离合器性能的相关因素。从工程实用的角度提出优化扭转弹簧的结构参数来改变踏板力学特性，保证离合器系统满足性能要求。对扭转弹簧进行运动分析并建立其力学模型，以扭转弹簧能够达到最大助力效果为原则，优化扭转弹簧安装角度；根据离合器设计约束条件，以扭转弹簧疲劳安全系数最大为目标函数，优化弹簧线径、中径、臂长和圈数等参数。将改进后的扭转弹簧重新装入踏板总成，通过测试平台验证了优化方案的可行性和合理性。

离合器；操纵机构；踏板；扭转弹簧；力学建模；参数优化

0 引言

离合器系统[1]包括离合器和操纵机构。离合器在汽车传动系统的动力切断与传递中起着重要作用。操纵机构始于离合器踏板，终止于分离轴承，把驾驶员对离合器踏板的输入转化成分离轴承上的输出，来控制离合器的分离和接合。

常小刚等[2]针对离合器系统测试中存在的问题，对离合器、主缸、副缸、液压管路和踏板箱部件的性能进行了分析，并优化了相关部件，但是从实用性上来说，改变主缸、副缸、踏板箱等成本较高。金鹏等[3]对离合器踏板进行测试试验，通过数据拟合的方法获得助力弹簧理想特性曲线，从而优化助力弹簧，但是未对操纵机构进行建模分析。扈静等[4]以汽车操纵装置的操纵力舒适性客观定量评价为研究目标，建立汽车整车操纵力舒适性评价模型，但未对操纵机构进行优化研究。马成等[5]计算踏板助力，并且对压缩弹簧进行建模，在Excel中不断调整压缩弹簧设计参数，获得理想助力曲线，但优化方法实现起来较繁琐。陈湘宾等[6]针对踏板力过大的问题，通过对离合器系统进行建模与分析，推导出最大踏板力理论计算公式。Hong等[7]对离合器膜片弹簧与操纵机构进行了力学建模，并对动态仿真结果与建模分析结果进行对比，验证了力学模型的正确性，但是操纵机构力学建模中未考虑助力弹簧的影响。Zhang等[8]用粒子群算法对离合器进行力学建模，得到分离轴承特性曲线，将仿真模型结果与测试结果进行比较，验证了力学模型的正确性，但是未对操纵机构进行建模分析。Lu等[9]基于USB高速采集技术开发了踏板力与位移测试系统，获得离合器踏板特性曲线与关键数据，但是测试系统不能采集分离轴承特性曲线与关键数据。Sfarni等[10]研究了膜片弹簧结构参数的改变对分离轴承特性曲线与踏板特性曲线的影响，但是通过改变膜片弹簧的结构参数来改变踏板特性曲线成本较高，实现起来较繁琐。

某品牌汽车离合器系统在样品台架测试中会出现最大踏板力过大、预紧力过小、踏板下降力过小等现象，针对这一问题，本文对离合器操纵机构进行了力学建模与分析，获得了影响踏板力的主要因素，从工程实用的角度出发，指出优化扭转弹簧力学特性可以方便解决问题，进而对扭转弹簧进行运动分析与力学建模。通过改变扭转弹簧的结构参数来优化扭转弹簧特性，从而优化踏板特性，使离合器满足性能要求。

1 离合器系统台架测试

1.1 台架测试方案

为了使某品牌汽车离合器系统样品能够正常工作，满足相关设计要求，搭建了离合器系统台架测试平台。将离合器系统样品安装在测试平台上，模拟其在整车上的安装状态，对离合器系统进行测试后，获得踏板力特性曲线、分离轴承特性曲线等相关参数。离合器台架测试平台如图1所示，踏板处和分离轴承处安装有传感器。

图1 离合器台架测试平台

离合器系统台架测试工作原理如图2所示。由工控机发出信号，运动控制卡控制电缸运动，电缸模拟人脚作为执行机构作用于踏板，在踏板运动的同时，压力传感器采集踏板力，位移传感器采集踏板位移；踏板力和位移通过操纵机构转换成离合器处的分离力和分离轴承位移。液压传感器采集分离力，位移传感器采集分离位移；采集的数据返回给工控机，通过测试系统显示试验数据。

图2 离合器系统台架测试原理图

1.2 试验结果分析

利用上述台架反复测试，获得踏板运动过程的踏板特性曲线(Ft-St)及关键数据如图3所示。特性曲线第一个波峰处的踏板力即为最大踏板力Ftmax，此时踏板位移即为Stmax。特征曲线与纵轴的交点(踏板位移瞬间为零即踏板刚开始运动时，传感器测得的瞬间踏板力近似等于预紧力)即为预紧力Fyj，踏板总行程记为Smax，最大踏板力与波谷处踏板力的差值即为踏板下降力Fj。

图3 操纵机构踏板特性曲线

台架测试不仅获得踏板特性曲线，而且获得分离轴承特性曲线(Ffl-Sfl)，如图4所示。

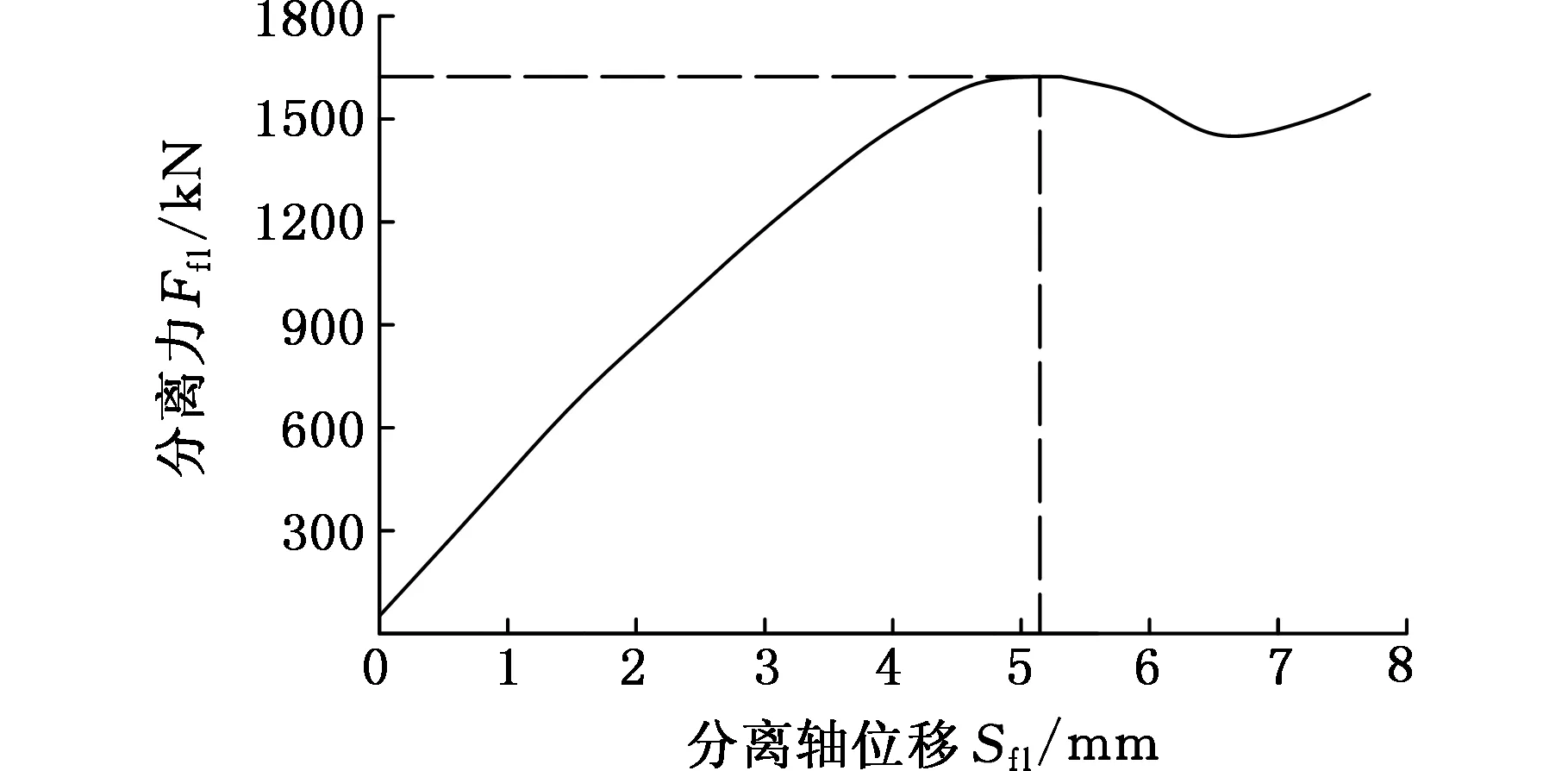
图4 分离轴承特性曲线

将试验结果与离合器系统性能参数设计约束值进行对比，结果见表1，可以看出，最大踏板力过大、预紧力过小、踏板下降力过小，不满足设计约束值。为了解决上述问题，需对操纵机构进行力学建模，分析并改进影响踏板特性曲线的相关因素，使得该离合器系统所有性能参数在设计约束值范围内，从而保证离合器系统的正常工作。

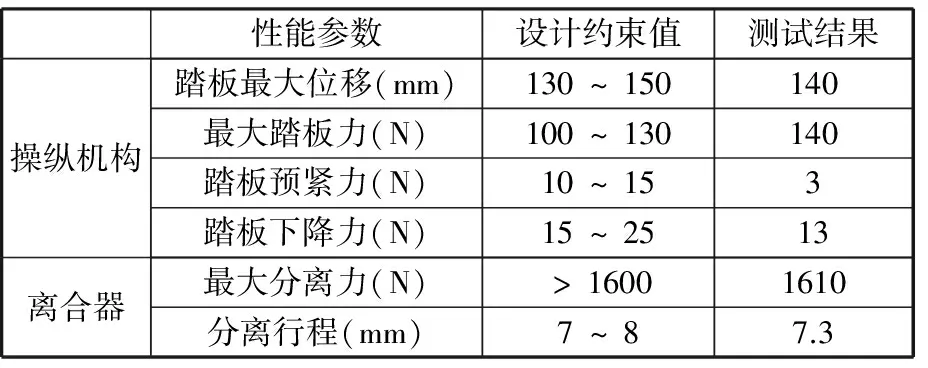
表1 离合器系统性能参数

2 操纵机构力学建模与影响因素分析

2.1 操纵机构力学建模

操纵机构如图5所示，包括踏板总成、主缸、油路、副缸、分离拨叉。踏板总成将踏板力与位移传递给主缸，主缸压缩油路将力与位移传递给副缸，副缸传递给分离拨叉，分离拨叉传递给分离轴承，分离轴承传递给离合器。

图5 操纵机构三维建模图

踏板总成是操纵机构的关键部件，包括踏板、踏板臂、旋转臂、扭转弹簧和安装架，如图6所示。踏板、踏板臂和旋转臂是刚性连接，通过O点安装在安装架上，在踏板运动过程中，O点为旋转中心，固定不动。G点为踏板力作用中心。A点为扭转弹簧在安装架上的初始安装点，可调节，但安装完成后则固定不动。B点是扭转弹簧与旋转臂的连接点，在踏板运动过程中B点绕O点做往复摆动。T为主缸与踏板臂连接点。

图6 踏板总成示意图

离合器踏板力Ft大小为

(1)

式中，Ffl为分离轴承处的分离力；iz为离合器操纵机构总传动比，iz=itiyib；it为踏板传动比，it=OG/OT；iy为液压传动比，iy=(d2/d1)2；d1为主缸直径；d2为副缸直径；ib为拨叉杠杆比；Fn为扭转弹簧间接作用在踏板上的力。

2.2 影响离合器系统因素分析

由式(1)可知影响踏板力的因素是Ffl、iz和Fn，即离合器本身、液压机构、分离拨叉和扭转弹簧等。从改动量最小和控制成本的工程应用角度来解决离合器踏板力过大、预紧力过小、踏板下降力过小的问题。若改变离合器本身结构(液压机构或分离拨叉)，成本高，不宜实施，即式(1)中的Ffl和iz的值不宜改变。本研究通过改变扭转弹簧结构参数来改变扭转弹簧的力学特性，即改变式(1)中的Fn值，从而改变Ft值，使最大踏板力减小，预紧力增大，踏板下降力增大，优化踏板特性曲线，从而满足离合器系统设计条件。

3 扭转弹簧的运动分析与力学建模

3.1 扭转弹簧运动分析

首先对扭转弹簧进行运动分析。图7中粗实线为扭转弹簧安装后的初始状态。其中O点、A点和B点即为图6中的相应点，BO为旋转臂长，∠ABO为扭转弹簧初始安装角度，E点为扭转弹簧的中心点，AC为扭转弹簧臂长。

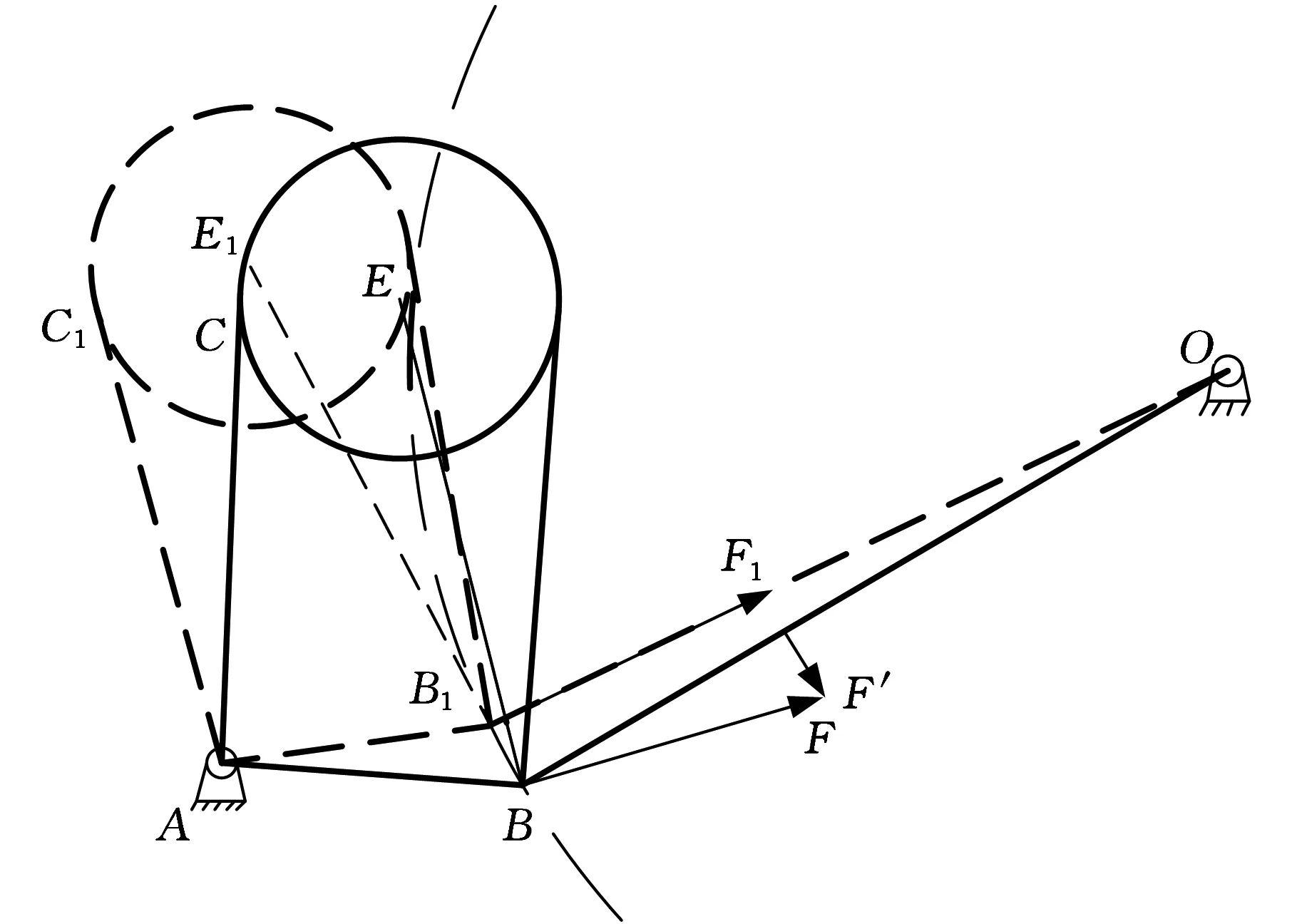
图7 扭转弹簧旋转简图(一)

当踩下离合器踏板时，旋转臂绕O点顺时针转动，B点随之顺时针转动，当B点移动到B1时，E点移动到E1点，C点移动到C1点，如图7所示。当扭转弹簧从B点向B1点运动时，扭转弹簧此时为压缩状态。取B点分析，此时扭转力为F，方向垂直于EB，扭转力F的切向分力F′垂直于BO，产生一个阻碍踏板的逆时针力矩，扭转弹簧在BB1段起到阻碍踏板转动的作用。当旋转至B1点时，此时E1B1垂直于B1O，扭转弹簧力F1的方向与旋转臂B1O在同一直线上，扭转力F1只有法向分力，没有切向分力，此时扭转弹簧对踏板既不增力也不助力。

B点继续旋转，当从B1点旋转至B2点时，E1点移动到E2点，C1点移动到C2点，如图8所示，扭转弹簧同样为压缩状态，产生一个有助于踏板转动的顺时针力矩，扭转弹簧在B1B2段起到助力的作用。当旋转至B2点时，扭转弹簧处于自由状态，不受压缩也不受拉伸，此时扭转力为零。

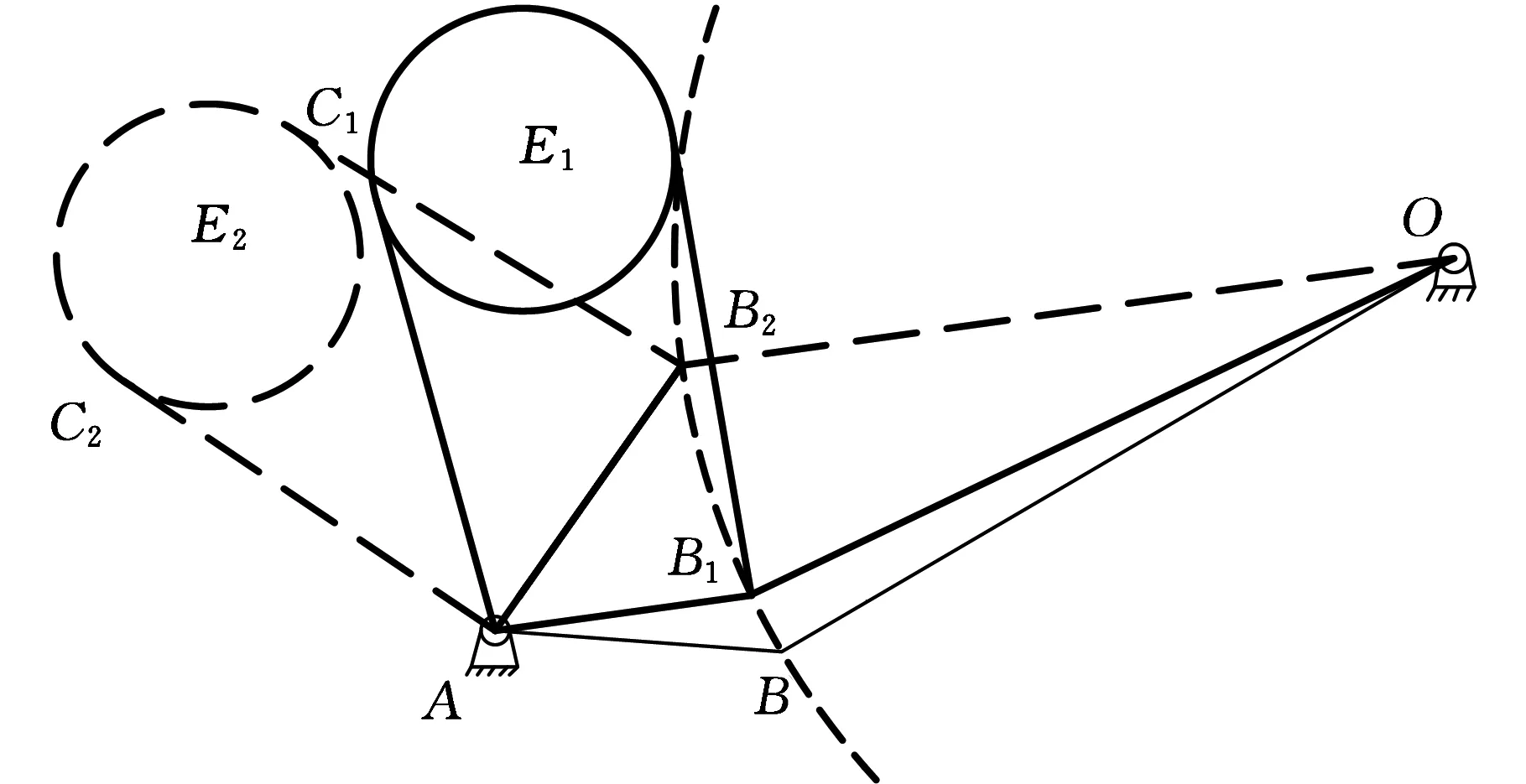
图8 扭转弹簧旋转简图(二)

B点继续旋转，当旋转至极限位置B3时，E2点移动到E3点，C2点移动到C3，如图9所示。扭转弹簧从B2移动到B3的过程中，扭转弹簧为拉伸状态。取B3点分析，此时扭转力为F3，方向垂直于E3B3，扭转力F3的切向分力F3′垂直于B3O，产生一个阻碍踏板转动的逆时针力矩，扭转弹簧在B2B3段起到阻力作用。

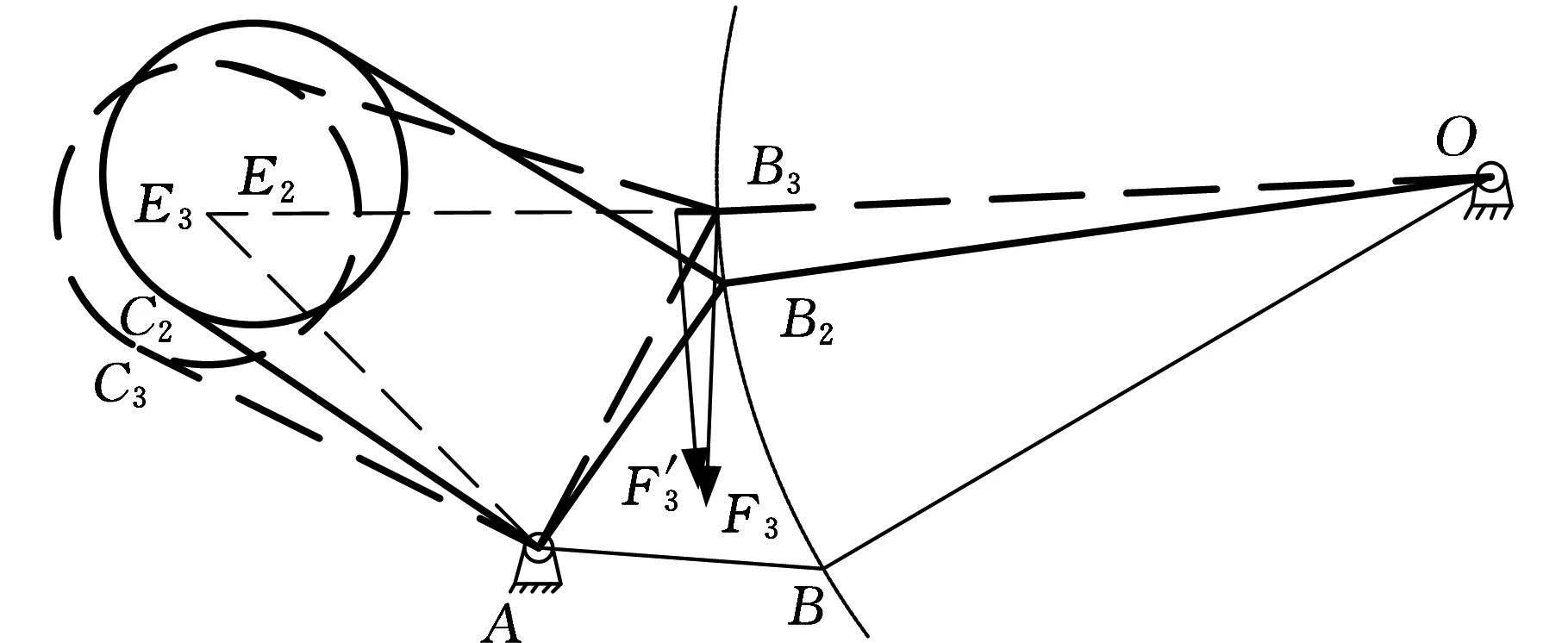
图9 扭转弹簧旋转简图(三)

3.2 扭转弹簧力学建模

如图10所示，将扭转弹簧旋转臂BO旋转至B4点的旋转角度∠BOB4记为α，进行力学建模。

图10 扭转弹簧力学建模

在图10中，已知的几何参数是：扭转弹簧中径D，即线段C4E4的长度为D/2；扭转弹簧臂长C4A记为l1；旋转臂的长度BO=B4O记为l2；安装点A(如2.1节所述，A点为扭转弹簧安装点，可调节，但安装完成后则固定不动)到旋转臂初始点B的距离AB记为l3；扭转弹簧初始安装角度∠ABO记为β。其他几何参数：扭转弹簧中心E4到安装点A的长度E4A记为a,旋转弦长BB4记为l4,AB4记为l5,∠C4AE4记为ν,∠B4BO=∠BB4O记为γ,∠ABB4记为φ,∠E4AB4=∠E4B4A记为ω,∠AB4B记为τ,扭转弹簧角度记为δ,均可通过已知参数由下面的公式求得：

(2)

(3)

(4)

(5)

φ=β-γ

(6)

(7)

(8)

(9)

δ=180°-2(ν+ω)

(10)

根据扭转弹簧公式[11]，扭转弹簧的力F4为

F4=kδ/a

(11)

其中，扭转弹簧弹性刚度为

(12)

式中，E为弹性模量；d为扭转弹簧线径；n为扭转弹簧有效圈数。

(13)

其中，扭转弹簧力F4与旋转臂OB4的夹角为

θ=360°-90°-ω-γ-τ

(14)

扭转弹簧转换为作用在踏板上的力Fn为

(15)

其中，旋转臂的长度l2是已知参数；lb为踏板臂长度即图6中的OG，也是已知参数。

踏板位移St即图6中G点的位移，可由下式计算得到：

St=αlb

(16)

若旋转到极限位置，即到达B3点，将极限角∠BOB3记为αmax，则踏板最大位移为Smax=αmaxlb。

需要说明的是，由于本文所述某品牌汽车离合器所用扭转弹簧臂长较短且线径较粗，故本文对扭转弹簧的力学建模忽略了扭转臂、弹簧圈的弯曲变形以及弹簧各圈间的摩擦力等因素。虽然模型存在一定的简化和理想化，但是经后续的理论计算及实验测试，验证了该力学模型正确有效。

3.3 实例计算

将某品牌汽车操纵机构参数代入扭转弹簧力学模型中，相关的参数如下：扭转弹簧弹性模量E=197 GPa，中径D=19 mm，线径d=3 mm，有效圈数n=4；扭转弹簧臂长l1=25 mm，旋转臂长度l2=51.2 mm，安装点到旋转臂初始点的距离l3=16.3 mm，初始安装角β=139.72°；踏板臂长lb=240.8 mm，极限角αmax=31.96°。将这些参数代入式(2)和式(16)中，用MATLAB软件进行计算，得到式(15)所示Fn与式(16)所示St扭转特性曲线，见图11。

图11 扭转弹簧特性曲线

扭转力为正，表示此时的扭转力为踏板阻力，反之为踏板助力。图11中,点B为该曲线与纵坐标交点，即为3.1节中的旋转臂的初始状态B点，此时踏板位移为零，扭转力即为预紧力Fyj。点B1为曲线与零线的第一个交点，对应的状态即为图7中的B1点，此时扭转力分力为零，对踏板既不阻力也不助力，从B到B1的过程中，扭转弹簧受到阻力作用。点B2为曲线与零线的第二个交点，对应的状态即为图8中的B2点，此时扭转力为零，弹簧处于自由状态，不受压缩也不受拉伸。从B1到B2的过程中，扭转弹簧受到助力作用。点B3为曲线的极限点，对应的状态即为图9中的B3点，从B2到B3的过程中，扭转弹簧受到阻力作用。P为最大助力处的点，该点即为最大踏板力处，对应的扭转力记为FP，踏板位移为SP。

3.4 扭转弹簧结构参数对结果的影响

根据3.2节的扭转弹簧力学建模，以及3.3节的实例计算，可以看出，决定扭转弹簧转换为作用在踏板上的力Fn的参数为：扭转弹簧弹性模量E、中径D、线径d、有效圈数n、扭转弹簧臂长l1、旋转臂的长度l2、安装点到旋转臂初始点的距离l3、初始安装角β、踏板臂长lb。从改动最小、成本最低的角度出发，仅仅改变β以及扭转弹簧的结构参数d、D、l1或n就能改变Fn，从而使离合器系统满足性能要求。

(1)改变安装角度β，线径d、中径D、臂长l1、有效圈数n保持不变。不同β的扭转弹簧特性曲线见图12。从图12中可以看出，β越大，助力效果越好，预紧力Fyj变大，最大助力FP变大，且SP变大。

图12 不同安装角度的扭转弹簧特性曲线

(2)改变线径d，安装角度β、中径D、臂长l1、有效圈数n保持不变。不同线径d的扭转弹簧特性曲线见图13。从图13中可以看出，d越大，助力效果越好，预紧力Fyj变大，最大助力FP变大，SP不变。

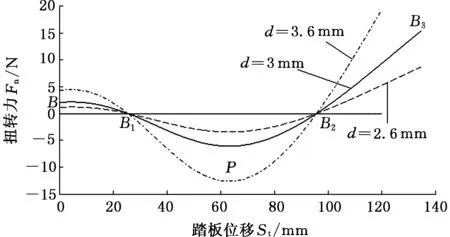
图13 不同线径的扭转弹簧特性曲线

(3)改变中径D，安装角度β、线径d、臂长l1、有效圈数n保持不变。不同中径D的扭转弹簧特性曲线见图14。从图14中可以看出，D越大，助力效果越好，预紧力Fyj变大，最大助力FP变大，SP大小基本不变。

图14 不同中径的扭转弹簧特性曲线

(4)改变臂长l1，安装角度β、线径d、中径D、有效圈数n保持不变。不同臂长l1的扭转弹簧特性曲线见图15。从图15中可以看出，臂长l1越小，助力效果越好，预紧力Fyj变大，最大助力

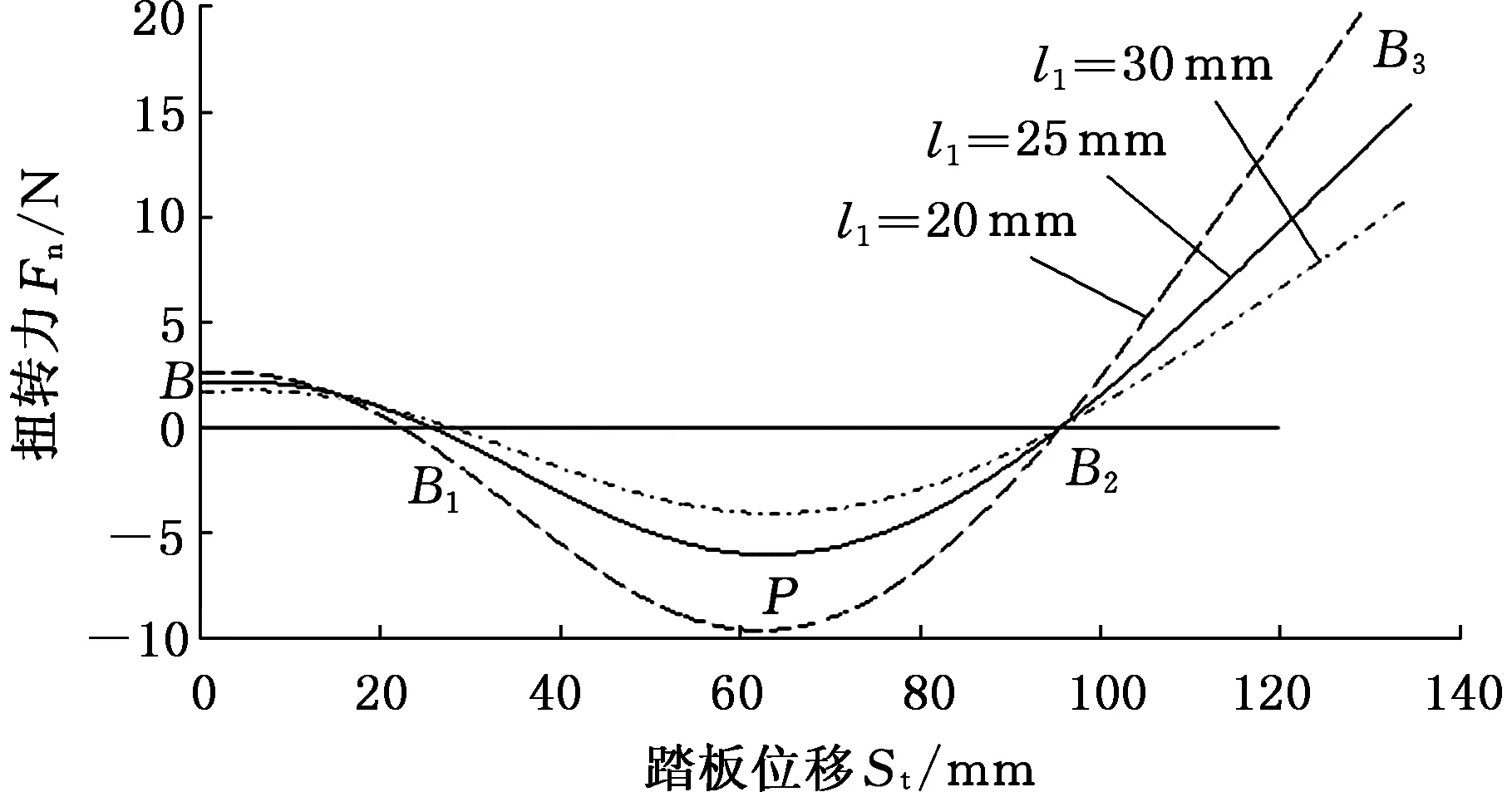
图15 不同臂长的扭转弹簧特性曲线

FP变大，SP不变。

(5)改变圈数n，安装角度β、线径d、中径D、臂长l1保持不变。不同圈数n的扭转弹簧特性曲线见图16。从图16中可以看出，圈数越小，助力效果越好，预紧力Fyj变大，最大助力FP变大，SP不变。

图16 不同圈数的扭转弹簧特性曲线

从图12～图16中可以得出，安装角度β决定SP的大小，而扭转弹簧的结构参数对其基本无影响。根据图3，操纵机构踏板力峰值处的踏板位移Stmax为90 mm，而图11中扭转弹簧最大助力处踏板位移SP为65 mm。未安装扭转弹簧时踏板峰值处的踏板位移记为S′，S′=85 mm。为了最大限度地减小最大踏板力，若SP=S′，扭转弹簧的助力峰值与踏板力的峰值叠加，则扭转弹簧能够达到最大助力效果。

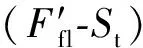
(17)

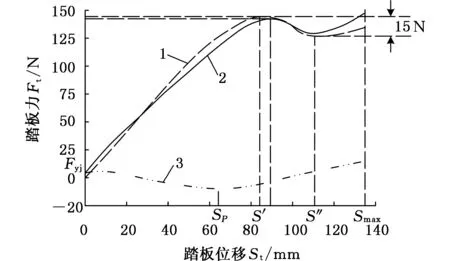
1.未安装扭转弹簧踏板特性 2.已安装扭转弹簧踏板特性 3.扭转弹簧特性图17 扭转弹簧特性曲线与踏板特性曲线

在图17中，未安装扭转弹簧踏板特性曲线波谷处对应的踏板位移记为S″，S″=100 mm，在后续调整踏板下降力时需用此量。将S′=85 mm代入式(16)可求得此时旋转角度α=20.21°，将α=20.21°代入式(15)，可求得扭转弹簧达到最大助力效果时的初始安装角度为118°。

4 扭转弹簧的优化

4.1 扭转弹簧设计变量

影响转扭力Fn的参数有β、d、D、l1、n，根据3.4节的论述，确定安装角度β=118°是优化结果，本节将对其余4个参数(线径d、弹簧中径D、臂长l1、圈数n)进行优化，选取这4个参数作为设计变量：

X=(d,D,l1,n)T

(18)

4.2 扭转弹簧目标函数

此扭转弹簧用于离合器系统，操作频繁，属于易导致疲劳损坏的弹簧，根据扭转弹簧的优化设计[11]原则，以疲劳安全系数S最大作为最优化设计的目标。

疲劳安全系数S[12]为

(19)

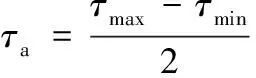
取ψτ=0.2，τ-1=0.6τ0(τ0为脉动疲劳极限，τ0=0.3σb，σb为抗拉强度)，代入式(19)得到

(20)

要使式(20)最大，分子为定量，只需分母最小，即扭转弹簧目标函数为

minf(X)=0.6τmax-0.4τmin

(21)

扭转弹簧应力τ计算如下：

(22)

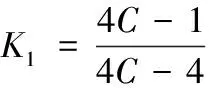
4.3 约束条件的确定

(1)离合器系统性能参数设计约束。根据表1某品牌离合器系统性能参数设计约束值，可知最大踏板力100 N≤Ftmax≤130 N，踏板预紧力10 N≤Fyj≤15 N，踏板下降力15 N≤Fj≤25 N。从图17中未安装扭转弹簧踏板特性曲线可知，最大踏板力为145 N，踏板预紧力为0，踏板下降力为15 N。根据表1的设计约束值与图17中未安装扭转弹簧踏板特性曲线，扭转弹簧特性曲线需满足如下约束：

当踏板位移SP=S′=85 mm时，要求

-45 N≤FP≤-15N

(23)

当踏板位移St=0时，要求

10 N≤Fyj≤15 N

(24)

当踏板位移S″=110 mm时，要求

-10 N≤Fn≤0

(25)

(2)扭转弹簧的强度条件约束如下：

(26)

其中，[σBP]为弯曲许用应力，本文所述扭转弹簧属于一类弹簧，查机械手册可得，[σBP]=0.6σb，σb=1400 MPa。

(3)弹簧线径约束为

1.5 mm≤d≤4 mm

(27)

(4)根据弹簧安装空间，弹簧中径约束为

15 mm≤D≤25 mm

(28)

(5)旋绕比C约束为

(29)

4.4 扭转弹簧优化结果

根据设计变量(式(18))、目标函数(式(21))、约束条件式(式(23)～式(29))，应用MATLAB优化工具箱对扭转弹簧进行优化求解，计算的最优化结果为X=(3.2 mm,20.3 mm,32.7 mm,4.8 mm)T，参照弹簧设计标准[12]，将结果调整为X=(3.2 mm,20 mm,30 mm,5 mm)T，优化结果如表2所示。

将扭转弹簧优化后的结构参数代入式(2)～式(15)，计算得到最大踏板力、预紧力和踏板下降力。将优化前的实验测试值与优化后的计算值进行对比，如表3所示。

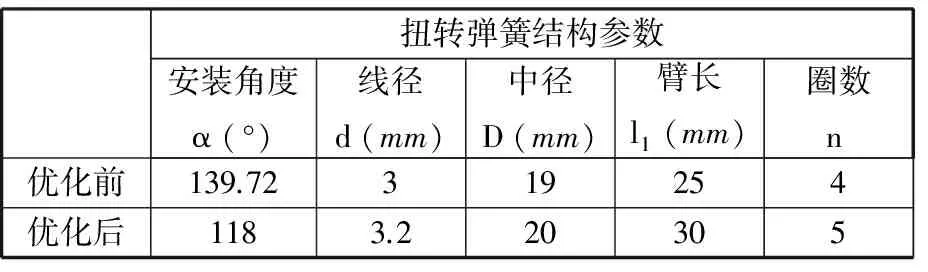
表2 扭转弹簧优化结果

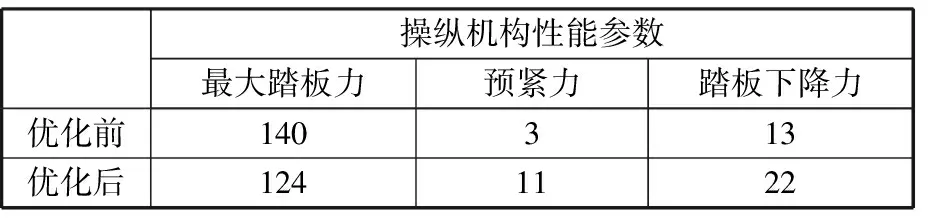
表3 操纵机构优化计算结果 N

将改进后的扭转弹簧装入踏板总成进行实验测试，实验曲线见图18。改进后预紧力为12 N，最大踏板力为126 N，踏板下降力为20 N。经验证，优化后的设计变量满足所有约束条件。

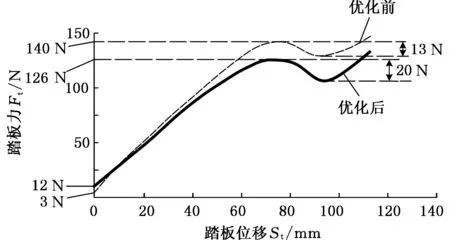
图18 优化前后踏板特征曲线实验对比

5 结论

(1)本文构建了某离合器系统测试平台，包括机械系统与测控系统。将离合器系统样品安装在测试平台上，模拟其在整车上的安装状态，对离合器系统进行测试，获得了踏板力特性曲线等相关数据，有效评判了离合器系统样品是否满足设计要求。

(2)对操纵机构进行力学建模，获得了影响踏板力的主要因素有离合器本身、操纵机构传动比和扭转弹簧。从改动量最小和控制成本的工程实用角度，得出优化扭转弹簧结构参数可以方便解决最大踏板力过大、预紧力过小、踏板下降力过小等问题。

(3)分析了扭转弹簧运动状态，建立其力学模型，得到扭转弹簧特性曲线。以扭转弹簧能够达到最大助力效果为原则，优化扭转弹簧安装角度；根据离合器设计约束条件，以扭转弹簧疲劳安全系数最大为目标函数，优化扭转弹簧线径、中径、臂长、圈数等参数，并将改进后的扭转弹簧重新装机并测试，优化后的扭转弹簧满足所有设计条件，离合器满足性能要求。

[1] 徐石安，江发潮. 汽车离合器[M]. 北京：清华大学出版社，2005.

[2] 常小刚，鲁统利. 汽车离合器分离系统测试与性能优化[J]. 传动技术，2013, 27(4):18-19. Chang Xiaogang, Lu Tongli. Testing Analysis and Optimization of Clutch Releasing System[J]. Drive System Technique, 2013, 27(4):18-19.

[3] 金鹏，张国耕，宋伟. 离合器踏板助力弹簧特性曲线优化[J]. 内燃机与动力装置，2014, 31(5):4-6. Jin Peng, Zhang Guogeng, Song Wei.The Optimization of Spring Characteristic Curve of Clutch Pedal[J]. I.C.E & Powerplant, 2014, 31(5):4-6.

[4] 扈静，刘明周，龚任波,等. 基于主成分分析的汽车操纵力舒适性分析与评价[J]. 中国机械工程，2011, 22(20):2456-2459. Hu Jing, Liu Mingzhou, Gong Renbo, et al. Evaluation of Vehicle Operating Force Comfort Based on Principal Component Analysis[J]. China Mechanical Engineering, 2011, 22(20):2456-2459.

[5] 马成，汪江，李光明,等. 离合踏板踏板力优化设计[J]. 农业装备与车辆工程，2015, 53(4):71-73. Ma Cheng, Wang Jiang, Li Guangming, et al. Optimization Design of Clutch Pedal Force[J]. Agricultural Equipment & Vehicle Engineering,2015, 53(4):71-73.

[6] 陈湘宾，张为民. 汽车离合器踏板力的实验研究及优化[J]. 机电一体化，2015(7)：25-28. Chen Xiangbin, Zhang Weimin. Vehicle Clutch Pedal Performance Optimization[J].Mechatronics, 2015(7)：25-28.

[7] Hong Y, Park H W. Simulation of Clutch Actuation System for Commercial Vehicle[J]. International Journal of Precision Engineering and Manufacturing，2010, 11(6):839-843.

[8] Zhang W B, Zhu G Y. Research and Application of PSO Algorithm for the Diaphragm Spring Optimization[C]// Fourth International Conference on Natural Computation. Jinan,2008:549-553.

[9] Lu Y, Guo B, Fan W,et al. Design and Realization of Testing and Analyzing Apparatus for Automobile Clutch[C]// International Conference on Digital Manufacturing & Automation. Zhangjiajie,2011:381-384.

[10] Sfarni S, Bellenger E, Fortin J, et al. Numerical and Experimental Study of Automotive Riveted Clutch Discs with Contact Pressure Analysis for the Prediction of Facing Wear[J]. Finite Elements in Analysis and Design, 2011, 47:129-141.

[11] 王灵犀，于海江，侯勇. 扭转缓冲器弹簧的多目标优化设计[J]. 沈阳理工大学学报，2013, 32(5):83-85. Wang Lingxi, Yu Haijiang, Hou Yong. Multi-objective Optimization Design of Springs in the Torsion Buffer[J]. Journal of Shenyang Ligong University, 2013, 32(5):83-85.

[12] 张英会，刘辉航，王德成. 弹簧手册[M].北京:机械工业出版社，2005.

(编辑 苏卫国)

Parameter Optimization of Torsional Spring in Clutch Operating Mechanisms

Zhu Wenbo Zhao Xixi Gan Yi Chen Long

University of Shanghai for Science and Technology, Shanghai, 200093

In order to evaluate the performances of an automobile clutch system, a testing platform of clutch system was established. The mechanisms of clutch system, which were simulated to install on a car, were tested with this platform and then the characteristic curve of pedal and the relative experimental data were obtained. It is found that pedal max-force is too large, the pre-tightening force is too small and pedal down force is too small. To solve these problems, a mechanics model of the clutch operating mechanisms was built and the relative factors which affected the performances of the clutch were analyzed. From the view of practical engineering, optimizing structure parameters of torsional spring were proposed to change pedal mechanical characteristics and ensure performance requirements of the clutch system. Motion state of torsional spring was analyzed and its mechanics model was built. Installation angle of torsional spring was optimized based on achieving maximum power effect. According to the design constraints of the clutch and the objective function of the maximizing fatigue safety factor of torsional spring, the torsional spring’s wire diameter, mean diameter, arm length and number of turns were optimized. The improved torsional spring was installed again in the pedal mechanism, and the optimization scheme was verified to be feasible and rational by the testing platform.

clutch; operating mechanism; pedal; torsional spring; mechanics modeling; parameter optimization

2016-01-08

上海市教育委员会科研创新一般项目(13YZ071)；国家自然科学基金资助项目(51375314，51475309)

U463.2；TH122

10.3969/j.issn.1004-132X.2016.23.005

朱文博，女，1973年生。上海理工大学机械工程学院副教授、博士。主要研究方向为数字化设计及制造。发表论文50余篇。赵熙熙，男，1991年生。上海理工大学机械工程学院硕士研究生。甘 屹，男，1974年生。上海理工大学机械工程学院副教授、博士。陈 龙，男，1978年生。上海理工大学机械工程学院副教授、博士。