钢绳环式无级变速器钢绳环轴向偏移分析

郭 卫 许晓彬 张 武 路正雄

西安科技大学，西安，710054



钢绳环式无级变速器钢绳环轴向偏移分析

郭 卫 许晓彬 张 武 路正雄

西安科技大学，西安，710054

针对钢绳环式无级变速器(WR-CVT)在传动比变化过程中钢绳环的轴向偏移限制了CVT速比变化范围和承载能力这一问题，以钢带环轴向偏移为参考，建立了钢绳环轴向偏移量计算模型，计算结果显示最大偏移量为0.6369 mm，最大偏移角为0.23°，该最大偏移量、最大偏移角较相同参数及条件下金属带式无级变速器(MB-CVT)钢带环的相应参数分别减小15.8%和0.04°。钢绳环在金属块鞍面圆弧槽内的滚动致使其承载能力优于钢带环。

无级变速器；金属带；钢绳环；轴向偏移

0 引言

自汽车诞生以来，无级变速传动系统一直是人们所追求的目标。相比于普通的有级变速传动，无级变速传动可显著提高汽车的经济性，改善汽车的动力性，并且大大减小驾驶员的工作强度。金属带式无级变速器(metal belt continuously variable transmission，MB-CVT)金属带的轴向偏移是无级变速器特定变速方式所导致的必然结果，轴向偏移限制了无级变速器的变速比和承载能力。在实际工作中，尽量减小甚至消除金属带的轴向偏移，可有效提升无级变速器的性能。

关于轴向偏移问题，目前已经有较为深入的研究。杨亚联等[1]比较了不同的偏移量计算方法对结果精度的影响；郭毅超等[2]对金属带的轴向偏移现象进行了描述并分析了其产生原因；王红岩等[3]在对轴向偏移量进行计算的基础上，提出了在常用速比范围内使金属带中心线轴向偏移量最小的优化方案；张伟华等[4-5]研究了锥盘母线与带的偏移量之间的关系；安颖等[6]对偏移量进行了解析计算，并结合实际情况，以绝对平均值最小为目标对偏移量进行优化。张武等[7]通过引入无接头钢丝绳和改变金属块形状，提出了一种新型金属带式无级变速器(wire rope CVT,WR-CVT)。

本文将在MB-CVT的理论基础上，建立WR-CVT偏移量的计算模型，并在传动比变化范围内，对比分析钢绳环与钢带环的轴向偏移情况,得出在相同条件下二者轴向偏移量的关系。

1 MB-CVT变速过程中金属带的偏移

如图1所示，当无级变速器处于工作状态时，金属块随着传动比的变化沿锥盘上下移动，使金属带产生径向和轴向位移。当传动比i=1时，金属带不偏移[8]。此时金属块侧边与锥盘的接触点为M，主动带轮、从动带轮的节圆半径均为RM。若主动轴上的锥盘向左移动S1，金属块与锥盘的接触点向外移动ΔR0，此时对称线向左移动S1/2，主动带轮上的节圆半径变为R1=RM+ΔR0。同时，从动轴上的移动锥盘向左移动S2，金属块与锥盘的接触点向内移动ΔRi，此时对称线向左移动S2/2，从动带轮上的节圆半径变为R2=RM-ΔRi。此时传动比i<1，为增速传动；反之，传动比i>1，为减速传动[9]。

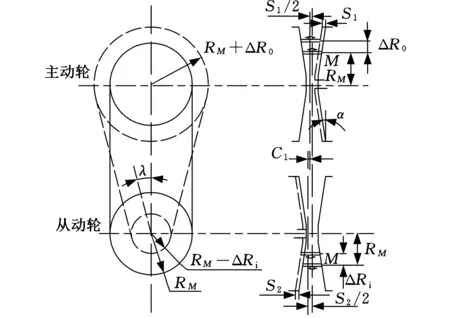
图1 直母线锥盘在变速过程中的金属带偏移

由于传动比变化过程中金属带的长度L保持不变，故有如下关系：

L=2Acosλ+(RM+Δh-ΔRi)(π-2λ)+

(RM+Δh+ΔR0)(π+2λ)=

2A+2π(RM+Δh)

(1)

ΔR0+ΔRi=Asinλ

(2)

式中,A为主、从动带轮中心距，mm；λ为金属带直线段与两带轮中心线的夹角；Δh为金属块鞍面与摆棱间的距离，mm。

将式(2)代入式(1)得

(3)

在直母线情况下，S1=2ΔR0tanα，S2=2ΔRitanα，当传动比i≠1，λ>0时，ΔR0<ΔRi，故S2>S1。因此当传动比i≠1时，金属带产生的轴向偏移C1为

(4)

式中，α为带轮母线与带轮轴线垂面的夹角。

在传动比为最大或最小时，金属带的轴向偏移量最大；当传动比i=1时，金属带不发生偏移。若在带长L的计算中计入偏移量的影响，则可以得到更精确的计算金属带轴向偏移量的计算公式[10]，经化简后如下：

(5)

2 WR-CVT变速过程中钢绳环的偏移

图2为WR-CVT的结构图。WR-CVT中的钢绳环对应MB-CVT中的钢带环，其在工作过程中产生轴向偏移的原理与MB-CVT相同；不同之处在于钢丝绳因其自身的性质，在产生轴向偏移的过程中会发生扭转，在摩擦力的作用下沿绳槽滚动[11-12]，而钢带环由于与金属块鞍面之间呈面接触，无法转动。因此用钢绳环替换钢带环，可以使轴向偏移量减小，从而减小带轮在工作过程中的功率损失，提高传递效率。

图2 WR-CVT结构图

2.1 钢绳环偏移理论分析

图3为主动带轮、从动带轮金属块绳槽的截面简图。主从动带轮上金属块绳槽底部圆弧段的中点分别为G、G′，G、G′点到带轮圆心的距离为R1、R2，B和B′为钢绳环与绳槽的切点，钢绳环与绳槽的切点到G点的垂直距离为f。

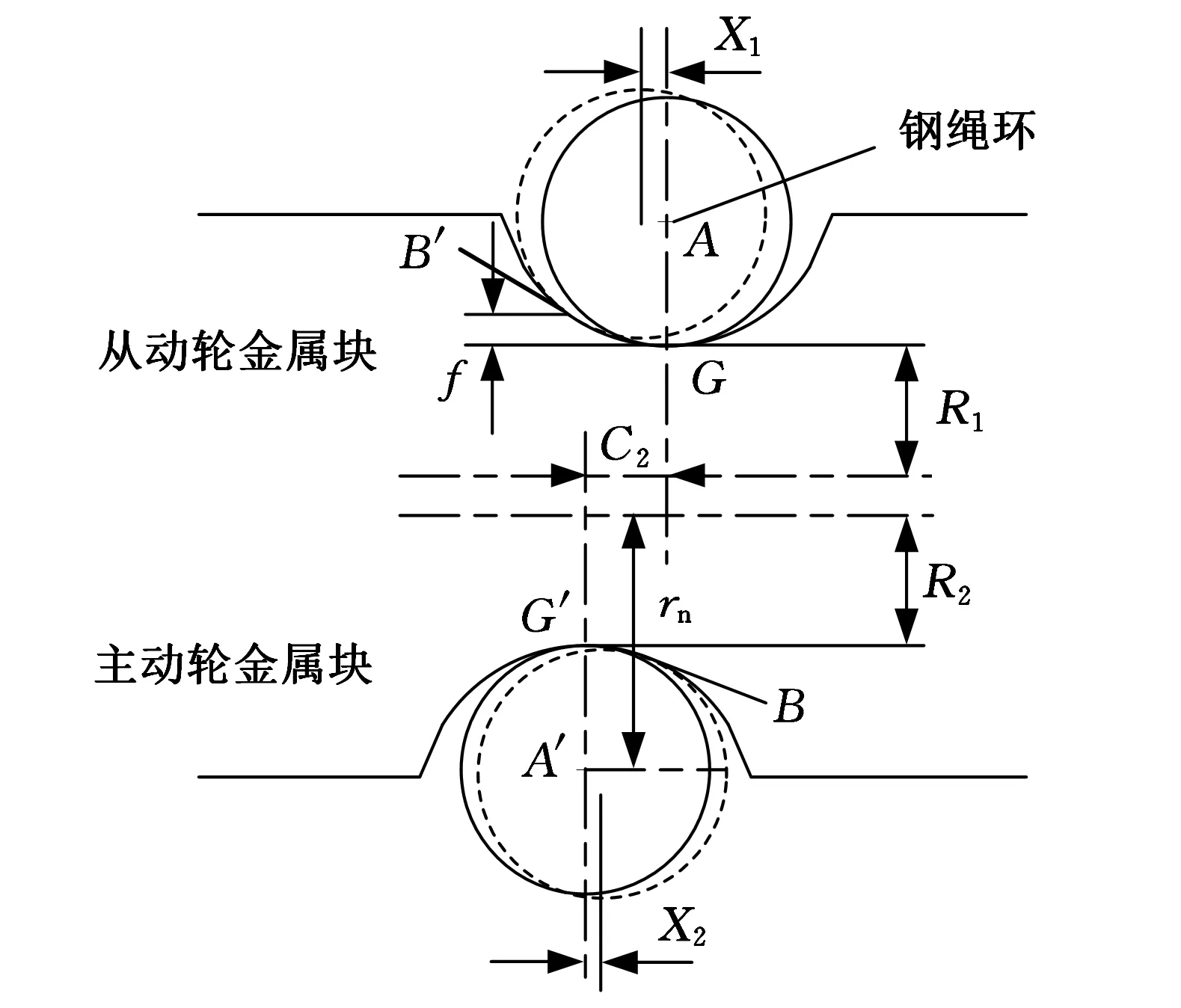
图3 主动带轮、从动带轮绳槽截面简图

当传动比i=1时，主动带轮与从动带轮的节圆半径相等，两带轮V形槽的对称线重合。此时钢绳环的圆心与绳槽的中心轴线重合，钢绳环产生的轴向偏移C2=0。传动比增大时，主动带轮的节圆半径减小，从动带轮的节圆半径增大，此时主动带轮、从动带轮V形槽的对称线不重合，钢绳环产生轴向偏移。由于钢绳环与金属块绳槽为点接触状态，并且自身具有扭转特性，当主动带轮、从动带轮金属块绳槽发生偏移时，在与绳槽之间摩擦力的作用下，钢绳环会沿绳槽圆弧段向减少偏移的方向滚动。当带轮产生C2距离的偏移时，钢绳环由图3中实线圆滚动到虚线圆所示位置。此时钢绳环的圆心到绳槽中心轴线的距离分别为X1和X2。随着传动比的增大，钢绳环滚动的距离也逐渐增大，当传动比最大时，钢绳环沿绳槽滚动的距离最远，此时X1、X2达到最大值。传动比由最大值变化到最小值的过程中，钢绳环的轴向偏移量先减小到0再增大，钢绳环沿绳槽滚动到另一侧的极限位置。由于金属带与金属块鞍面之间呈面接触，不能发生移动或滚动，因此其实际的轴向偏移量即为主动带轮、从动带轮的轴向偏移量；钢绳环在绳槽中会向减少轴向偏移的方向滚动，并且带轮的偏移量越大，其滚动的距离越大。因此钢绳环的实际轴向偏移量为

(6)

2.2 计算模型

如图4所示，将带轮上的金属块视为连续的，则钢绳环在金属块绳槽中的滚动情况与滑轮中的变化类似[11]。在传动比最大的情况下，半径为r的钢绳环绕入底径分别为R1、R2的绳槽，此时钢绳环的偏角φ也为最大。

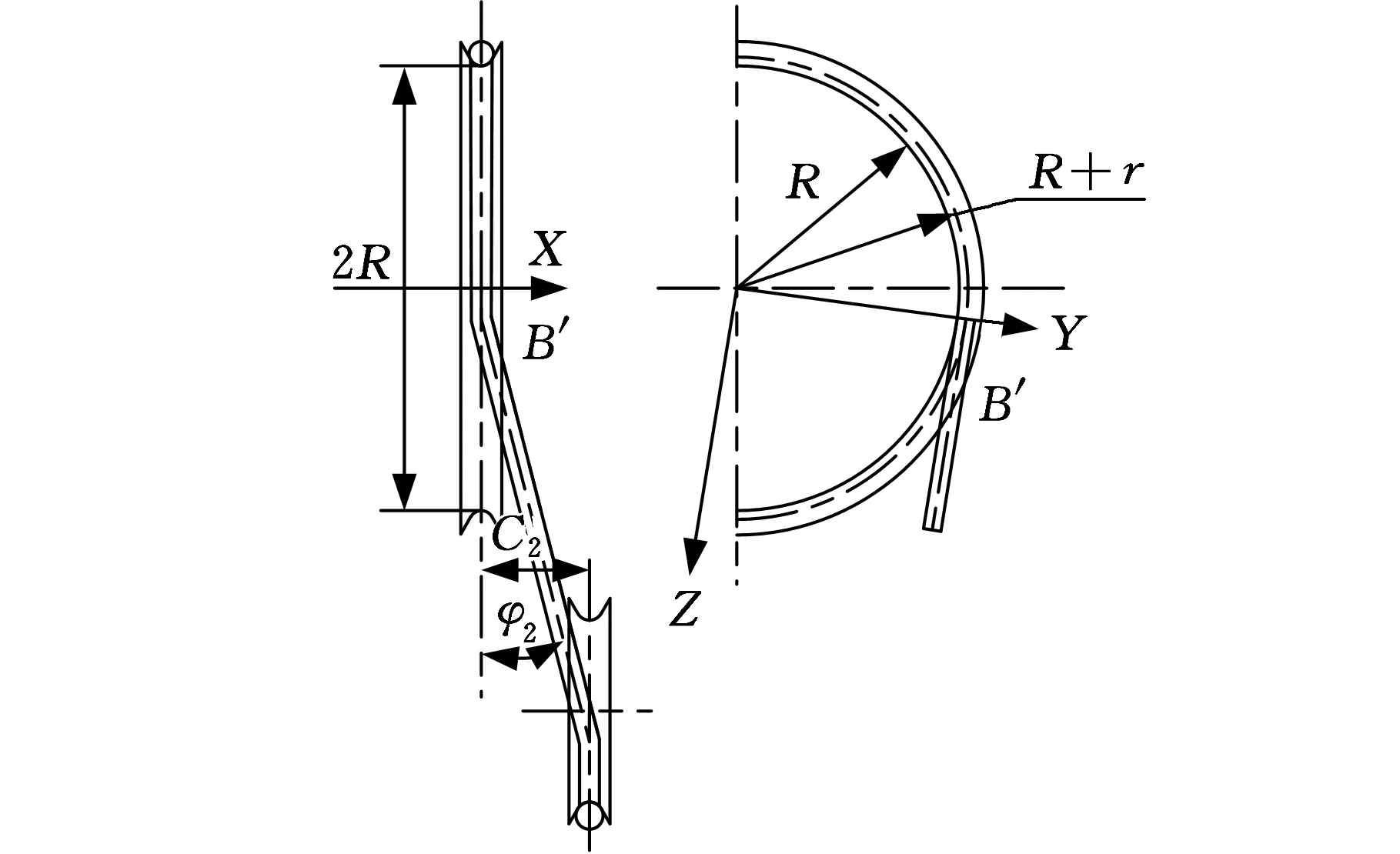
图4 钢绳环绕入无级变速器

对于主动带轮，以带轮轴心线为圆心，轴心线到钢绳环圆心的距离为半径rn，则

(7)

结合图3，可以得出钢绳环中心线方程：

(8)

式中,x为钢绳环沿X轴的偏移距离；y为钢绳环中心线在主动轮上的弯曲半径；z为沿Z轴方向钢绳环与主动带轮、从动带轮切点之间的距离；r′为绳槽圆弧段半径；R为带轮中心轴线到G点的距离。

对于从动带轮，根据钢绳环中心线也可以建立类似方程，只是R值不同。并且在传动比确定之后，主动带轮、从动带轮中钢绳环的偏斜角度φ相等。

2.3 参数确定

本文中钢绳环的型号采用6×7 IWS，其结构如图5所示。

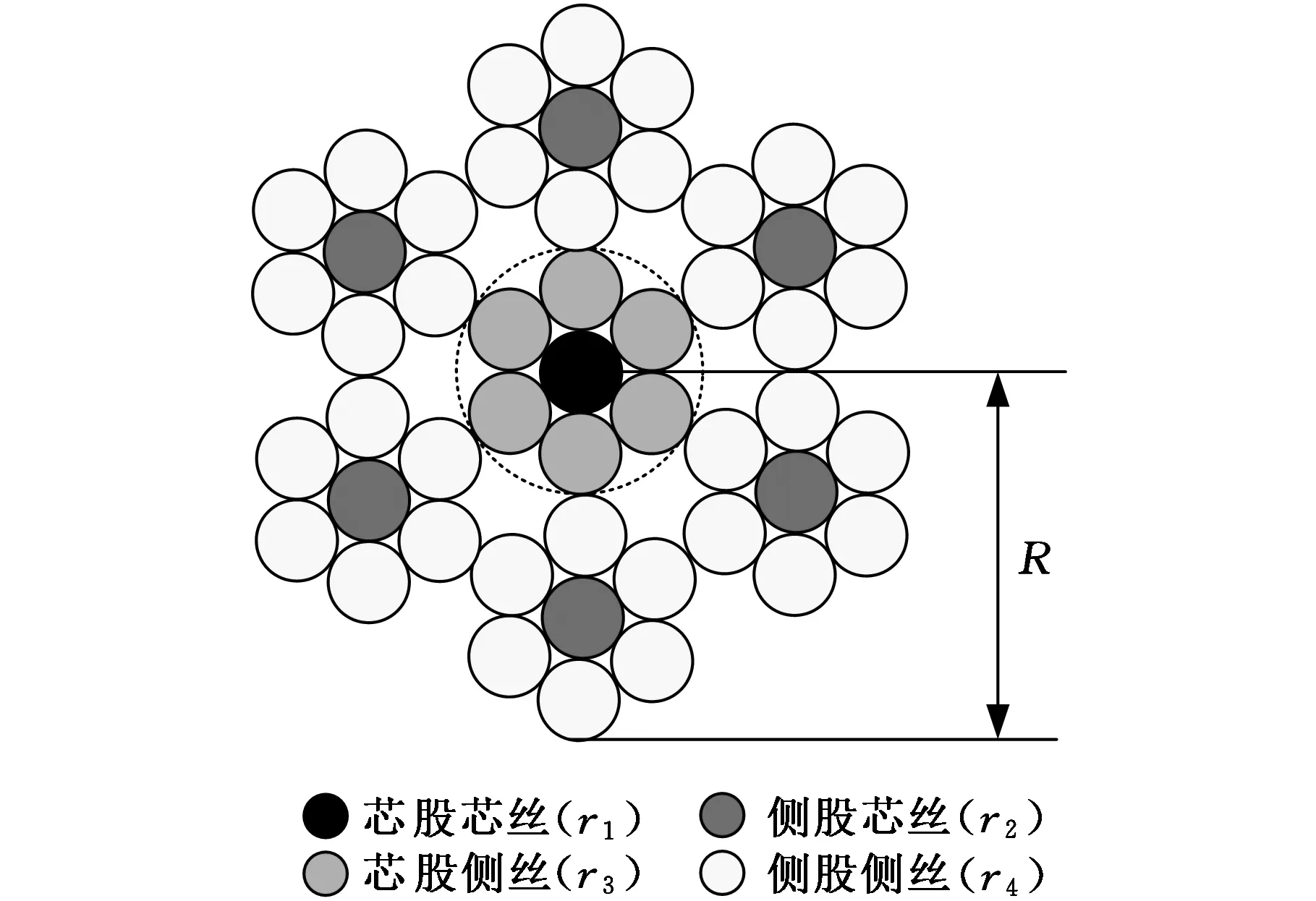
图5 6×7 IWS钢绳环结构图

图5中r1、r2、r3、r4分别为芯股芯丝、芯股侧丝、侧股芯丝和侧股侧丝的钢丝半径，其半径为1.30 mm、1.25 mm、1.10 mm、1.05 mm。因此钢绳环半径r=r1+2r2+2r3+4r4=10.2 mm。根据JB/T 9005.1-1999 《绳槽断面标准》可得绳槽底部圆弧段半径r′为11.5 mm。本文选用VDT公司的P811型CVT为对象，传动比变化范围为0.42～2.35。根据传动比的变化，主动带轮、从动带轮的节圆半径R1、R2的变化见表1。

表1 主动带轮、从动带轮节圆半径与传动比的关系 mm

3 钢绳环与钢带环偏移分析

将表1中的数据代入式(5)～式(8)，可计算出在不同传动比下钢带环和钢绳环的轴向偏移量及偏移角度。计算结果见表2、表3。

表2 轴向偏移量与传动比的关系

表3 偏移角度与传动比的关系

iφ1(°)φ2(°)0．420．270．230．690．0550．0460．8500．0110．0091．2200．0160．0131．4400．0530．0451．7200．1140．0962．1400．2130．1802．3500．2600．220

注：φ1、φ2分别表示金属带和钢丝带的偏移角。

由表2、表3可得：

(1)当传动比由小到大变化时，钢绳环的偏移量与钢带环的偏移量变化趋势一致，都由最大值减小到0再增大，与理论分析结果一致。

(2)在传动比i≠1时，钢绳环在摩擦力的作用下会沿绳槽发生滚动，因此钢绳环的轴向偏移量较钢带环有所减小，并且在传动比i=0.42时减小量最大，为15.8%。

(3)当传动比最小时，主动带轮的节圆半径最大，从动带轮的节圆半径最小。此时主动带轮上钢绳环与绳槽接触点的位置高于从动带轮上的接触点位置，可得出带轮的节圆半径对钢绳环在绳槽中的滚动距离有一定影响。传动比一定时，节圆半径大的带轮上钢绳环滚动的距离较大。

(4)相比于金属带式无级变速器，钢绳环式无级变速器的轴向偏移情况有所改善，使得无级变速器在传动过程中功率损失较少，带轮的传动能力有一定的提高[13]。

图6、图7所示为钢带环和钢绳环的轴向偏移量及偏移角。由图6及图7可以明显看出,钢绳环的轴向偏移量及偏移角相比于钢带环较小，当传动比接近1时，因为主动带轮、从动带轮中心轴线的偏移较小，所以钢带环和钢绳环的轴向偏移量较为接近。但随着传动比的变化，主动带轮、从动带轮节圆半径的差值越大，钢绳环的轴向偏移量和偏移角减小得越多。

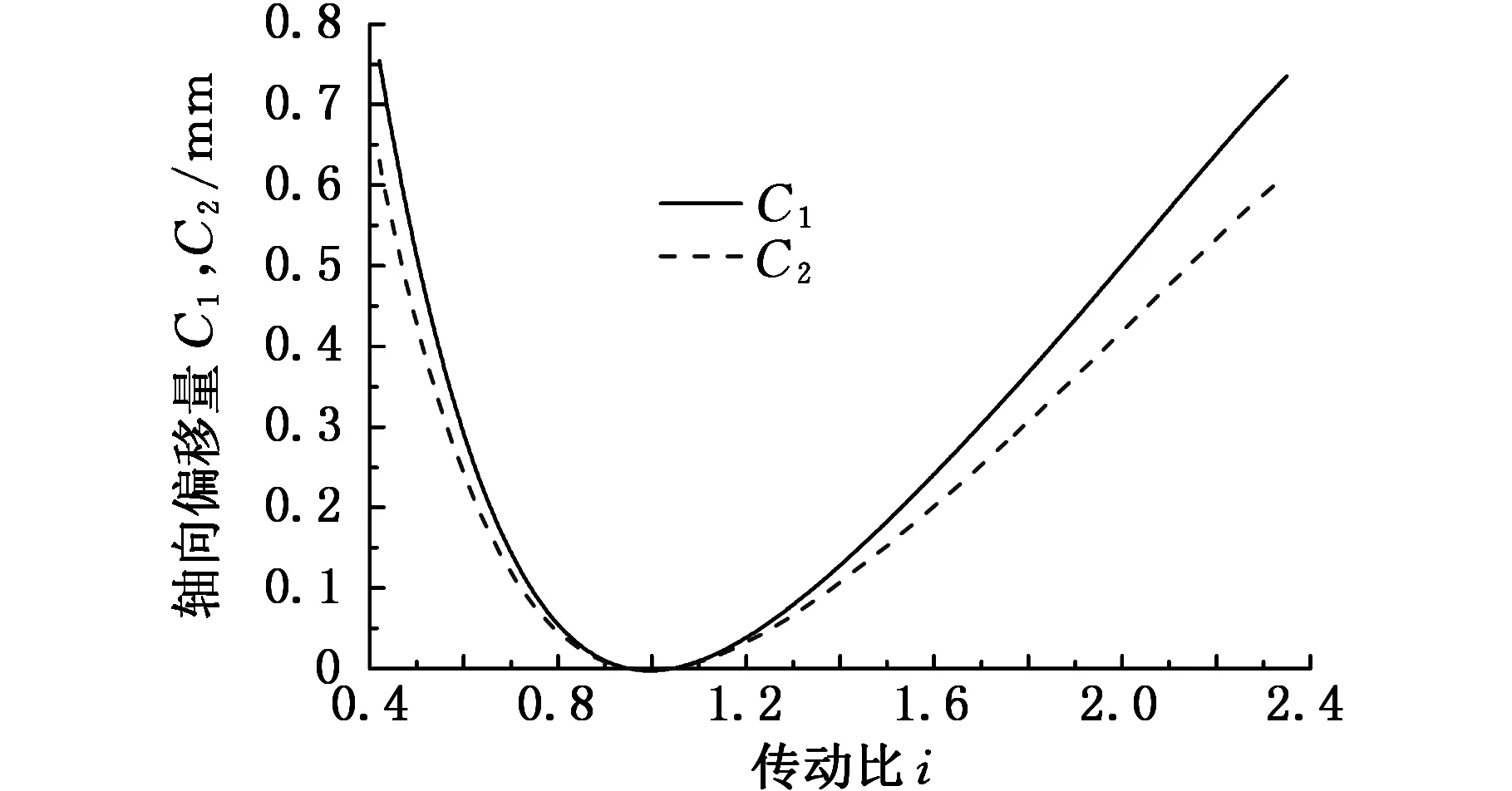
图6 轴向偏移量随传动比变化曲线

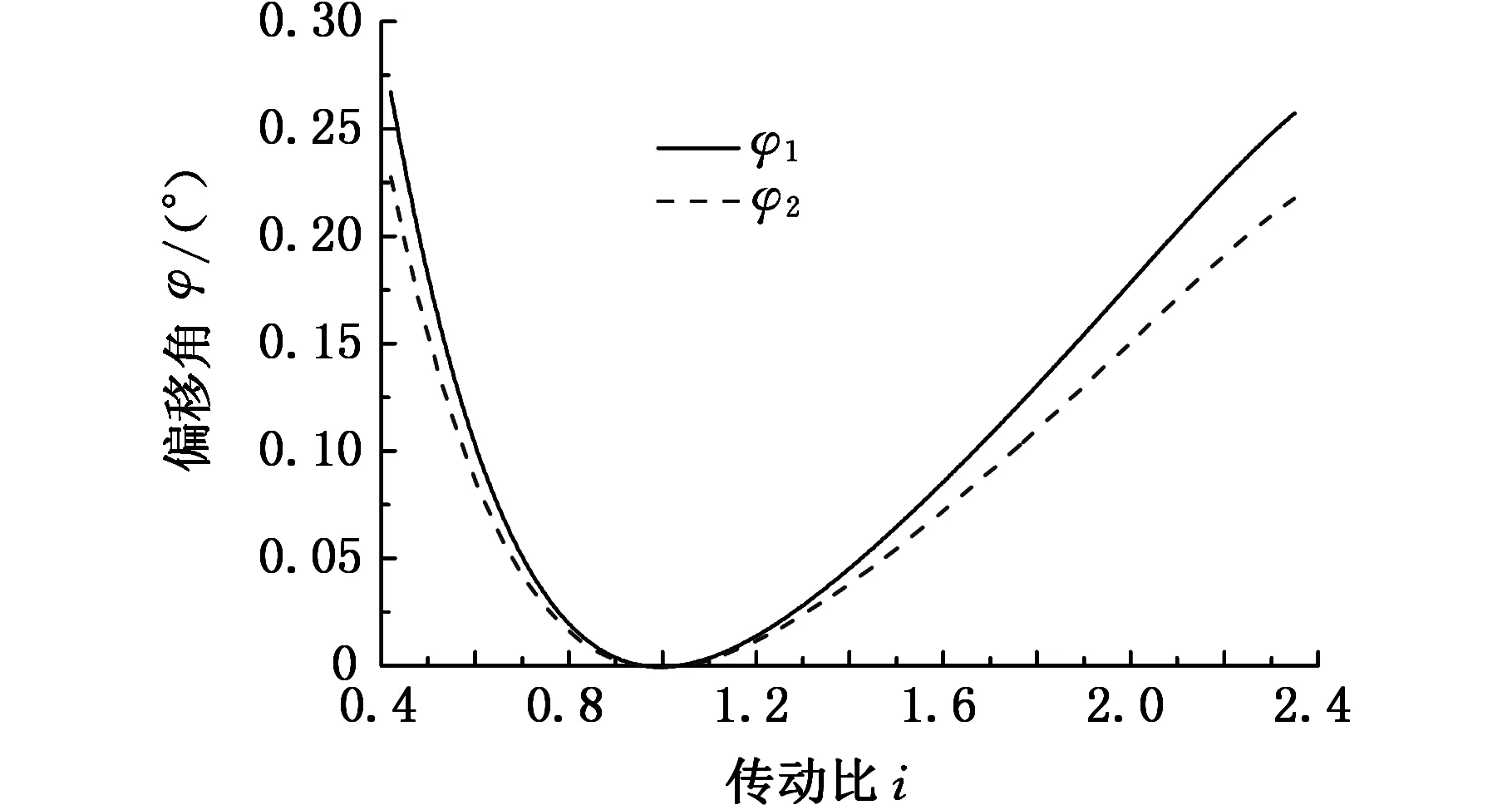
图7 偏移角随传动比变化曲线

4 结论

(1)在传动比确定的情况下，WR-CVT钢绳环轴向偏移量较钢带环的轴向偏移量小，且在传动比达到最大或最小时偏移量的减小量达到最大值。

(2)为防止钢带环之间及钢带环与金属块之间发生轴向窜动，钢带环与金属块的鞍面都有一个弧度，使钢带环嵌在金属块鞍面上。在发生轴向偏移时，钢带环会承受附加侧向弯曲应力，严重影响钢带环的受力状态，直接影响金属带的承载能力和寿命。由于与钢绳环配套的金属块切有绳槽，钢绳环在绳槽中可以转动，故在很大程度上减小了附加侧向弯曲应力带来的影响。

(3)轴向偏移量对变速器的承载能力有较大影响。因此在偏移量相同的情况下，WR-CVT钢绳环的承载能力要优于MB-CVT钢带环。

[1] 杨亚联,秦大同,王红岩,等. CVT无级变速传动钢带的轴向偏移分析[J]. 重庆大学学报(自然科学版),1999,22(6):1-7. Yang Yalian, Qin Datong, Wang Hongyan, et al. Analysis of Misalignment of Metal Pushing V-belt of Continuously Variable Transmission[J].Journal of Chongqing University,1999,22(6):1-7.

[2] 郭毅超 ,何维廉 ,黄宏成. 金属带式CVT的钢带轴向偏移分析[J]. 传动技术,2001(4):43-47. Guo Yichao, He Weilian, Huang Hongcheng. The Analysis of Alignment of the Metal Pushing Belt Type Continuously Variable Transmission[J].Drive System Technique,2001(4):43-47.

[3] 王红岩,杨志华,白雪,等. 金属带式无级变速器装置带轮工作面形状与带轴向偏移的分析[J].吉林工业大学学报,1997(4):17-22. Wang Hongyan, Yang Zhihua, Bai Xue, et al.Analysis of the Surface Shape of the V-sheave and the Belt Misaligrnment in the Metal V-belt CVT[J]. Journal of Jilin University of Technology,1997(4):17-22.

[4] 张伟华,程乃士,谢里阳. 直母线锥盘金属带式无级变速器带的轴向偏移分析[J]. 中国机械工程,2007, 18(8): 1005-1007. Zhang Weihua, Cheng Naishi, Xie Liyang. Analysis of Axial Deviation of the Belt in a Metal V-belt CVT with Straight Generatrix Cones[J].China Mechanical Engineering,2007,18(8):1005-1007.

[5] 张伟华,程乃士,孙德志,等. 金属带式无级变速器锥盘母线的设计方法[J]. 东北大学学报,2001, 22(3): 279-281. Zhang Weihua, Cheng Naishi, Sun Dezhi, et al. Design Method of Cone Disc Generatrix in a Metal V-belt Continuously Variable Transmission[J].Journal of Northeastern University,2001,22(3):279-281.

[6] 安颖,宋传学,高帅. CVT金属带偏移量计算及其优化[J]. 汽车技术,2009(2):26-29. An Ying, Song Chuanxue, Gao Shuai.Computation and Optimization of CVT Misalignment[J].Automobile Technology, 2009(2):26-29.

[7] 张武，郭卫，路正雄，等．一种新型金属带式无级变速器设计与分析[J]．机械传动，2015，39(9)：59-61. Zhang Wu, Guo Wei, Lu Zhengxiong, et al. Design and Analysis of a New Type of Metal Belt Continuously Variable Transmission[J]. Journal of Mechanical Transmission,2015,39(9)：59-61.

[8] Zang F, Wu Z. Control Study on the CVT Metal V-belt’s Axial-misalignment of Car[C]// Intelligent Vehicles Symposium. Xi’an, 2009:1389-1393.

[9] Zang F Y. Simulation and Fuzzy Control Study on the CVT Metal V Belt Axial Misalignment of Car[J]. Key Engineering Materials, 2010, 426/427: 97-101.

[10] Zang F Y. Simulation Research of the Electro-hydraulic Control System of CVT Metal V-belt’s Axial Misalignment[C]//International Technology and Innovation Conference. Xi’an, 2009:556.

[11] 陈坚,薛磊. 偏角对钢丝绳负面影响的新指标[J]. 起重运输机械,2013(3):43-48. Chen Jian, Xue Lei. The New Norm of the Negative Effect of Deflection Angle on Wire Rope[J].Hoisting and Conveying Machinery,2013(3):43-48.

[12] 李海波,白剑波,韩梦丹,等. 起重机钢丝绳允许偏角的探讨[J]. 起重运输机械,2015(5):43-46. Li Haibo, Bai Jianbo, Han Mengdan, et al. The Investigate of the Permit Deflection Angle on Wire Rope of the Crane[J]. Hoisting and Conveying Machinery,2015(5):43-46.

[13] 张发军,刘中,周长,等. CVT金属带轴向偏斜对功率损失影响的研究[J]. 机械传动,2013(6):13-16. Zhang Fajun, Liu Zhong, Zhou Chang, et al. Research on the Influence of Axial Oblique Position on Power Loss Mechanism in CVT[J]. Journal of Mechanical Transmission, 2013(6): 13-16.

(编辑 王旻玥)

Analysis of Wire Rope Ring’s Axial Misalignment in WR-CVT

Guo Wei Xu Xiaobin Zhang Wu Lu Zhengxiong

Xi’an University of Science and Technology, Xi’an, 710054

Axial misalignment of the wire rope CVT(WR-CVT) in the processes of changing the transmission ratio would limit the CVT speed ratio ranges and bearing capacity. To solve this problem, based on the axial misalignment of the metal belt ring, a calculation model of wire rope axial misalignment was established. The results indicate that the maximum displacement is as 0.6369 mm,and the maximum offset angle is as 0.23°. The value is 15.8% smaller than the maximum displacement and 0.04° smaller than the maximum offset angle respectively under the same parameters and conditions of the metal belt CVT(MB-CVT) wire rope. The bearing capacity of the wire rope ring is better than metal belt ring due to the rolling in the saddle surface arc groove of the metal.

continuously variable transmission(CVT); metal belt(MB); wire rope ring(WR); axial misalignment

2016-01-22

国家自然科学基金资助项目(51505373);陕西省教育厅科研计划资助项目(15JK1490)

TH132

10.3969/j.issn.1004-132X.2016.23.007

郭 卫，男，1955年生。西安科技大学机械工程学院教授、博士研究生导师。主要研究方向为煤矿机械、矿山机械提升设备。发表论文50余篇。许晓彬，男，1991年生。西安科技大学机械工程学院硕士研究生。张 武，男，1985年生。西安科技大学机械工程学院副教授。路正雄，男，1986年生。西安科技大学机械工程学院博士研究生。