电动汽车车身的回传射线矩阵刚度链分析方法

陈毅强 刘子建

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082



电动汽车车身的回传射线矩阵刚度链分析方法

陈毅强 刘子建

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

基于LifeDrive纯电动汽车模块化结构形式，通过拓扑优化得到一款纯电动汽车车架结构；建立了基于梁单元的车架结构回传射线矩阵计算模型；由模型得到车架梁单元尺寸以及车身与车架之间的多个耦合力，以更合理的刚度链方法优化了车身简化模型的主断面参数；利用有限元方法计算了车身与车架的承载度。结果证明设计的车架与车身结构满足目标承载度和刚度性能的要求，该方法为非承载式电动汽车车身及车架的概念设计提供了参考。

纯电动汽车；车架设计；承载度；回传射线矩阵法

0 引言

能源危机和环境保护要求汽车产品向微型化、低排放方向发展，作为解决能源和环保问题方案之一的电动汽车越来越受到人们的关注。纯电动汽车车身的正向设计技术已成为各国汽车研发的一个重点。

新型材料的应用、客户需求多样化正在影响纯电动汽车车身结构朝着模块化、平台化方向发展。典型的如宝马i系列车采用了LifeDrive架构，它由Life和Drive两个独立的模块组成，Life模块是乘员舱部分，采用超轻量化且高强度CFRP碳纤维复合材料构成，Drive模块包括悬架、蓄电池组、驱动系统和碰撞防护结构等。

这种模块化架构车辆采取非承载式车身时，通常认为载荷均由车架承担，并没有考虑车身的承载作用。此外，如何合理设计纯电动汽车的车架，目前还没有成熟的理论和方法[1]。

国内外学者研究车身及车架设计优化方法取得了多项进展。如田海豹[2]提出了用于车身结构概念设计阶段的刚度链方法，通过建立以主断面、接头等为节点的车身刚度链模型，进行车身载体刚度优化和轻量化设计，并给出了承载式车身设计的实例。文献[2]使用传递矩阵法计算车身刚度，用于梁结构分支较多的非承载式电动车车架分析时会产生子刚度链分解复杂、计算效率低的问题。扶原放等[3]依据微型电动汽车车架结构的受力特性及材料性能要求，考虑多种行驶冲击载荷对车架的作用，建立了设计优化数学模型。高云凯等[4]基于拓扑优化方法研究了某非承载式电动汽车车身。周姗姗[5]利用客车有限元模型，基于车身承载度分析对车身结构进行了改进研究。Cavazzuti等[6]基于有限元方法研究了以车架结构性能为约束、以质量为优化目标的汽车底盘框架结构的设计方法。Hodkinson等[7]研究了电动汽车的轻量化设计流程、车身结构分析方法以及有限元仿真方法。梁晨等[8]以某非承载式车身及车架为例，利用有限元方法研究了弯曲和扭转工况下的车身及车架对整车的刚度贡献率。

如何在非承载式车身的概念设计阶段就充分考虑车架和车身对于载荷的贡献，形成合理的设计方法，并获得车身整体轻量化效果，这一问题仍然没有较好的解决方法。因此，研究非承载式车身与车架承载度优化分配的方法，以及先进的车架设计方法，对于提升纯电动汽车整车轻量化水平和综合性能都具有重要意义。

1 车架结构设计

1.1 承载度分配与刚度设计目标值的确定

本文研究的纯电动汽车结构形式如图1所示，车架承载度设计流程如图2所示。

图1 纯电动汽车结构形式

图2 承载度设计流程

在总体结构方案基本确定的情况下，选择不同的车身承载度目标值会得到不同的车身与车架的质量比。本文研究A00级电动汽车，参考文献[8]中的非承载式SUV车身对整车刚度的贡献，设定车身与车架承载度的目标比值为3∶7，车身与车架通过接口连接，前座椅中心位置下方为挠度测量点，根据文献[9]中电动汽车设计过程中的性能指标确定方法，此处最大挠度设定为0.497mm。考虑弯曲工况下的载荷为多点集中载荷，分析过程中可将车身、车架都按照简支梁计算。先绘制车架简化受力图(图3)，此时可得车架的弯曲刚度计算公式[9]：

图3 车架受多点集中载荷受力图

(1)

式中，EI为弯曲刚度值，N·m2；yx为测定点挠度值，m；x为前轴中心位置到测定点的距离，m；l为轴距，m；Pi为各点加载载荷，N；ai为前轴中心到加载点的距离，m；bi=l-ai，m；j为前轴前载荷项数；k为至挠度测定点的载荷项数；n为后轴前载荷项数；m为总载荷项数。

由式(1)计算出EI=2.76 MN·m2。车架承载度目标值为0.7时，测量点最大挠度约束值为1.43yx=0.7115mm。

根据普通车型扭转刚度结果统计数据[10]，此A00级车扭转角目标值θ不应超过0.5°，前悬架支座处位移可表示为

ΔL=(b/2)tanθ

(2)

其中,ΔL为前悬支座位移;b为前悬支座间距。本文中b=610mm，由式(2)可计算出前悬支座处最大位移约束为2.71mm。

1.2 拓扑优化设计

车架所受静载荷F1包括乘客、电池组、电机的载荷，大小约为4500N，如表1所示。

表1 主要载荷部件

部件名称数量质量(kg)位置电池包165车架中部电机驱动系统140前轴中部电机控制器15前轮内侧乘员及座椅4340车架中部

载荷均施加于设计域的上表面，并将电池对车架的载荷考虑为多点集中载荷[11]，加载方向均垂直于地面。在静载荷基础上对模型施加弯矩载荷F=1.8F1与扭转载荷M=0.5F2l，其中F2为前轴载荷。根据刚度和频率要求，以结构整体的体积约束作为优化的目标函数，以结构的刚度最大化作为优化的约束条件，以前座椅测量点处挠度及前悬支座处最大位移为边界条件[12]，建立拓扑优化的设计域，如图4所示。

图4 车架拓扑优化设计域

选择材料为45钢，弹性模量为200GPa，泊松比为0.3，屈服强度为355MPa。刚度约束条件下以体积为目标函数，刚度要求为约束条件(文中反映为测量点挠度及最大扭转角度)，单元密度为设计变量；频率约束条件下以一阶模态频率为目标函数，体积分数为约束条件，单元密度为设计变量，设定收敛容差为0.001，若两次迭代之差小于0.001，则认为优化收敛并停止计算[12]。经迭代计算后单元密度取0.17，优化结果如图5所示。

图5 车架结构材料分布

考虑各总成的布置以及工艺要求，采用截面为矩形的型钢制作车架，将拓扑结构简化成图6所示的形式，但此时只确定了车架的结构形式，还没有确定矩形钢管的厚度，因此还需要进一步的优化设计。

图6 车架结构图

2 基于刚度链的车架建模与分析

图6所示车架模型的分支梁较多，当一个节点与多个单元相连时，采用基于传递矩阵的刚度链方法建模时不易确定传递路径和节点的传递矩阵[13]，且计算量大，而利用回传射线矩阵法(methodofreverberaton-raymatrix,MRRM)则可以避免这些缺陷。MRRM方法对所有单元列相位关系的列式方式与对所有节点列散射关系的方式相同，总体相位矩阵和散射矩阵分别是将各节点的局部相位矩阵和散射矩阵放置在矩阵的对角线上得到的分块对角矩阵，列式非常统一。MRRM基本思路是：依据两组关系建立整体结构的回传矩阵，第一组关系为节点的近端位移和远端位移的关系，由节点的力和力矩的平衡关系建立；第二组关系为杆件的近端位移与远端位移的关系，由局部坐标系的设定得到。由回传矩阵即可求得整体结构各节点的位移和内力的精确解[14]。

2.1 结构描述

将梁的中心线相连，得到车架结构的简化线框模型，节点以大写字母I、J、K…表示，则杆件表示为〈I,J〉、〈J,K〉等。图7中，各杆件的编号表示为〈1,2〉，〈2,3〉，…，〈27,28〉。

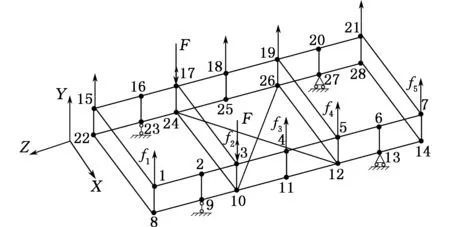
图7 车架简化线框模型

车架结构节点总数为28，梁单元总数为48，f1～f5为车身与车架之间的耦合力，利用对称关系，先考虑1/2模型的分析。

2.2 建模方法

2.2.1 定义坐标系

首先，对车架结构建立整体坐标系(X,Y,Z)，如图7所示。以与节点1相连的三根梁为例，对梁单元建立对偶坐标系，如图8所示，各梁单元的长度记为l〈1,2〉，l〈2,3〉，…，l〈27,28〉。

图8 梁单元局部坐标系

2.2.2 单元物理量的表示方法

在整体坐标系(X,Y,Z)下，定义节点J(J=1,2,…,28)的广义力和广义位移向量分别为

(3)

其中，pJ中包含沿X轴、Y轴、Z轴的集中力和绕三个坐标轴的力矩，uJ中包含沿X轴、Y轴、Z轴三个方向的位移和转角。

在局部坐标系(x,y,z)〈J,K〉下，梁单元任意截面的广义力和广义位移向量分别为

(4)

其中，f〈J,K〉中包含z方向的轴力、x和y方向上的剪力、绕z轴的扭矩、绕x和y轴的弯矩；δ〈J,K〉中包含三个沿x、y和z轴的线位移和三个绕x、y、z的转角。

2.2.3 力平衡关系与位移协调关系

车架结构的梁与梁之间的连接点简化为无集中质量的刚性节点，在节点J处有平衡关系：

(5)

式中，T〈J,K〉为66阶转换矩阵；F〈J,K〉为节点J处61阶内力向量，包含轴剪力和扭矩弯矩和；F为外力向量；fi(i=1,2,3,4,5)为车架与车身的耦合力向量。

(6)

A〈J,K〉和D〈J,K〉由空间杆系结构的刚度矩阵得到：

A〈J,K〉=

(7)

D〈J,K〉=

(8)

式中，EA、GJ分别为车架梁单元的抗压刚度和剪切刚度。

根据式(5)和式(6)可得第一组关系，即包含节点近端位移、远端位移的力和力矩平衡关系：

(9)

(10)

式中，mJ为与节点J相连的杆件数量。

在节点3与节点17处，F≠0，fi≠0；在节点1、4、5、7处，F=0，fi≠0；其他节点处，F=0，fi=0。

除了上述力和力矩平衡关系外，车架的梁结构在连接节点处还满足位移协调条件:

(11)

(12)

2.2.4 车架结构的回传矩阵

通过力平衡方程式(9)和位移协调方程式(11)可得到节点的波源向量s和传递分配矩阵S。则有如下关系：

a=Sd+s

(13)

其中，a和d是所有节点的近端位移向量aJ与远端位移向量dJ组成的向量：

(14)

式(13)中有12mJ个方程，24mJ+5个未知数，分别为节点近端和远端沿三个坐标轴方向上的位移、转角、力和力矩，如果考虑5个未知耦合力，则还需要建立另外一组关系。

在局部坐标系中，杆件的远端位移可以用近端位移表示：

d=PUa

(15)

对于某一杆件〈J,K〉，式(15)中的d包含节点J的远端位移d〈J,K〉实际上是节点K的近端位移a〈K,J〉，但两者可能存在正负号的差异。利用相位矩阵p可以将两者关系表示为

d〈J,K〉=pa〈J,K〉

(16)

J=1,2,…,mJK=1,2,…,n

式(15)中的U为转列矩阵，用于改变向量a中元素的排列次序，使之与向量d中的元素相对应，例如d〈J,K〉对应a〈K,J〉；P为整体相位矩阵，表示为

P=diag(p,p,…,p)

由式(12)和式(15)可得：

a=(I-R)-1s

(17)

R=SPU

式中，I为6×6阶单位矩阵。

由于耦合力未知，为了避免未知数个数多于方程个数，需要确定弯曲工况下部分节点的位移。根据已确定的车架最大挠度以及边界条件进行三次拟合可以近似得到车架弯曲工况下的变形曲线，如图9所示。

图9 车架结构变形拟合曲线

由图9可以得到yi(i=1,3,4,5,7)，即节点1、节点3、节点4、节点5、节点7在整体坐标系中沿Z轴负方向的位移：

(18)

由于与节点1、3、4、5和7连接的单元的近端或远端状态向量a〈J,K〉中的元素v〈J,K〉可以由拟合曲线的坐标得到，由式(13)和式(15)可以得到的12mJ个方程中，含12mJ个未知数,其中包含5个已知的节点位移v1、v3、v4、v5、v7，其大小对应式(18)中的y值和5个未知的耦合力。车架梁截面采用30 mm×30 mm的矩形，厚度设为t，因此由不受外力作用的节点的关系可解出梁单元厚度t。由式(17)可以得到a, 由式(13)可以得到d，将a和d代入式(9)可得到内力向量F〈J,K〉，由此可以求得车架结构与车身结构之间的耦合力fi。

3 刚度分析与承载度验证

参考白车身弯曲刚度试验加载方法[15]，加载力F=3000N，加载点位于前座椅安装位置左右对称处，方向垂直向下(整体坐标系Y轴负方向)。根据式(9)、式(15)、式(16)和式(18)解得梁单元厚度ti以及车身与车架之间耦合力fi如表2所示，fi为正值表示其为拉力，为负值表示其为压力。车架最终梁单元厚度t取3.686mm。

表2 车架梁单元厚度及车身与车架耦合力

耦合点挠度yi梁厚度ti(mm)耦合力fi(N)y13．560-169．680y24．110233．480y33．4905．116y43．74029．490y53．530-101．280

为了达到设定的承载度目标值，需要优化车身在耦合力fi(i=1,2,…,5)作用下的主断面参数，车身结构采用基于线框的简化几何模型，简化模型梁单元的中心线由车身A级曲面(图10)上采集的特征点连接而成，并且遵照以下简化原则：①先考虑车身主要承载梁结构，暂不考虑地板、顶盖等覆盖件；②暂不考虑焊点特性；③曲梁用多段直梁近似逼近。车身侧围及顶板的梁单元分布参考传统车型，底板梁单元分布根据乘员座椅位置及与车架的接合位置确定，得到车身梁单元简化模型如图11所示。

图10 车身A级曲面

图11 车身梁单元分布及主断面位置

在车身刚度链分析方法[16]中，只在前座椅中心处施加垂直于地面向下的载荷。对于本文研究的非承载式电动汽车车身，在进行车身的截面优化时，需要用f1、f2、f3、f4、f5代替弯曲工况下座椅安装点处左右对称的加载力F，将耦合力加载到车身与车架的接合点后的力学模型上，如图12所示(图12a为文献[2]和文献[17]中模型加载方式，图12b为本文对应的加载方式)。车身主断面简化为薄壁矩形，如图13所示。

[17]的车身刚度链计算方法，以轻量化为目标建立约束函数，优化设计模型如下：

(a)车身刚度链单元划分及加载方式[17]

(b)非承载式车身刚度链单元划分及加载方式图12 车身刚度链单元划分及加载方式

图13 简化梁截面

(19)式中，Δz为位于前座椅中心处的测量点最大挠度，其大小不应超过车身与车架整体变形时的约束值4.97×10-4m;ΔL为前悬支座处位移量。

利用MATALB遗传算法工具箱计算各主断面的最优截面尺寸，计算结果如表3所示。根据表3中的计算结果可以得到主断面面积A、惯性矩Iy=∫Ay2dA、惯性矩Iz=∫Az2dA和极惯性矩Ip=∫A(y2+z2)dA在车身主断面节点上的分布情况，如图14所示。

根据图14可以看出，编号为3、8、10、12的梁对车身刚度影响较为显著。这与此类车身梁单元刚度灵敏度分布情况[17]吻合，说明优化结果合理。

为验证上述方法的准确性，利用ANSYS分别建立车身、车架以及车身与车架耦合的beam188梁单元模型，弯曲工况下变形云图见图15～图17，车身与车架耦合整体扭转工况下的变形云图见图18。

根据位移云图得到前座椅中心测量点处变形量如表4所示，测量点处的挠度在容许的变形范围内，扭转工况下前悬支座处位移ΔL=2.627mm<2.71mm,满足扭转性能要求。

表3 车身主断面截面参数 mm

图14 主断面面积、惯性矩和极惯性矩分布情况

图15 弯曲工况下车身变形

图16 弯曲工况下车架变形

图17 弯曲工况下车身与车架耦合变形

图18 扭转工况下车身与车架耦合变形

根据基于刚度的承载度评价方法,车架的刚度与车身及车架总体刚度的比值即为车架的承载度[18]，根据式(1)分别得到车架的弯曲刚度K1=2.803MN·m2、车身和车架耦合整体的弯曲刚度K=3.84MN·m2。可以计算出车架弯曲刚度与整体弯曲刚之比即承载度为0.73，与设定的目标承载度非常接近，满足设计要求。

表4 测量点挠度值 mm

4 结语

本文根据LifeDrive模块化车架的载荷情况，拓扑优化后得到了电动汽车车架结构。建立了车架的回传射线矩阵计算模型，当车架梁结构变动时，只需增加或减少相应的方程即可，避免了基于传递矩阵法的刚度链方法难以确定车架载荷的传递路径和计算量大的缺陷，便于建立车架与车身之间的耦合计算模型。本方法用于非承载式车身整体的优化设计，明显拓展了车身刚度链设计方法的应用范围，提高了计算效率。最后，利用有限元方法计算验证了实例车身、车架简化模型刚度与承载度的分配满足预先设定的目标值要求。

参考文献：

[1]SchelkleE,ElsenhansH.VirtualVehicleDevelopmentintheConceptStageCurrentStatusofCAEandOutlookontheFuture[C]//3rdMSCWorldwideAerospaceConference&TechnologyShowcase.Toulouse,2001:24-26.

[2] 田海豹. 基于刚度链方法的车身概念设计研究[D]. 长沙：湖南大学, 2013.

[3] 扶原放, 金达锋, 乔蔚炜. 微型电动车车架优化设计研究[J]. 机械制造, 2009, 47(1):12-15.FuYuanfang,JinDafeng,QiaoWeiwei.MiniResearchElectricVehicleFrameOptimizationDesign[J].MachineManufacturing, 2009, 47(1):12-15.

[4] 高云凯, 邵力行, 张海华. 微型电动车非承载式车身轻量化研究[J]. 汽车工程, 2008, 30(9):808-810.GaoYunkai,ShaoLixing,ZhangHaihua.DevelopmentofSkeletonStructurefortheFrame/bodyConstructionofaMiniElectricVehicle[J].AutomotiveEngineering, 2008, 30(9):808-810.

[5] 周姗姗. 基于车身承载度的半承载式客车结构改进研究[D]. 长春:吉林大学,2011.

[6]CavazzutiM,MerullaA,BertocchiE,etal.AdvancedHighPerformanceVehicleFrameDesignbyMeansofTopologyOptimization[C]//Internati-onalConferenceonStructuralEngineering,MechanicsandComputation.CapeTown,2010:279.

[7]HodkinsonR,FentonJ.LightweightElectric/HybridVehicleDesign[M].Atlanta:Elsevier, 2001:36-70.

[8] 梁晨, 何宁宁, 姚俊贤. 非承载式车身对整车刚度贡献率研究[J]. 机械强度, 2009, 31(6):887-891.LiangChen,HeNingning,YaoJunxian.StudyonStiffnessContributionofSeparateTypeBodytoWholeFrame-bodyStructure[J].MechanicalStrength, 2009, 31(6):887-891.

[9] 乔蔚炜, 金达锋, 于兴林. 微型电动车车身结构优化设计中性能指标的确定方法[J]. 天津汽车, 2008(8):36-38.QiaoWeiwei,JinDafeng,YuXinglin.ResearchonPerformanceDeterminationMethodofaMiniElectricCarBody[J].TianjinAuto， 2008(8):36-38.

[10]PorscheEngineeringServices.Ulsab-Avc-PesEngineeringReport[R]. 2001:731-800.

[11]HifnieMAI.DesignandAnalyzetheChassisofanElectricVehicleforUseinCampusCondition[J].Utem, 2009(1):46-54.

[12] 扶原放, 金达锋, 乔蔚炜. 微型电动车车架结构优化设计方法[J]. 机械工程学报, 2009, 45(9):210-213.FuYuanfang,JinDafeng,QiaoWeiwei.OptimazationMethodforaMiniElectricVehicleFrameStructure[J].JournalofMechanicalEngineering, 2009, 45(9):210-213.

[13] 郭永强. 回传射线矩阵法的理论及其应用[D]. 杭州：浙江大学, 2008.

[14]McGuireW,GallagherRH,ZiemianRD.MatrixStructuralAnalysis[M]. 2nded.Amazon:CreateSpace, 2000.

[15] 林智平.JL030轿车白车身结构优化研究 [D]. 长春: 吉林大学, 2011.

[16] 刘子建, 周小龙, 田海豹, 等. 基于主断面刚度优化分配的车身正向概念设计[J]. 中国机械工程,2015,26(6):837-843.LiuZijian,ZhouXiaolong,TianHaibao,etal.ForwardConceptualDesignofCarBodyUsingStiffnessOptimalAllocationofMainSections[J].ChinaMechanicalEngineering, 2015,26(6):837-843.

[17]EuropeanAluminiumAssociationStiffnessRelevanceandStrengthRelevanceinCrashofCarBodyComponents[R].Nordrhein-Westfalen:UniversityofAachen, 2010.

[18] 林标华, 姚成. 基于刚度的客车车身承载度评价[J]. 客车技术与研究, 2014, 36(4):7-9.LinBiaohua,YaoCheng.EvaluationofCoachBodyworkLoadingDegreeBasedonStiffness[J].Bus&CoachTechnologyandResearch, 2014, 36(4):7-9.

(编辑 王旻玥)

AnalysisMethodofReverberation-rayMatrixStiffnessChainforElectricVehicleBodies

ChenYiqiangLiuZijian

StateKeyLaboratoryofAdvancedDesignandManufactureforVehicleBody,HunanUniversity,Changsha, 410082

BasedonLifeDrivepureelectricvehiclemodularstructures,apureelectricvehicleframestructurewasobtainedbytopologyoptimizationmethod.Thereverberation-raymatrixmodelofframestructurewasestablishedbasedonthebeamelements.Accordingtothereverberation-raymatrixcalculationmodel,thethicknessesoftheframebeamelementsandtheforcesbetweenthebodyandframewereobtained,themainsectionalparametersofsimplifiedmodelofvehiclebodywasoptimizedwithamorereasonablemethod.Theloadingdegreebetweenbodyandframewascalculatedbyfiniteelementmethod.Resultsshowthattheframeandthebodystructuresmeettherequirementsofthetargetloadingdegreeandstiffnessperformance,andthismethodprovidesreferencetothebodyandframeconceptualdesignofelectricvehicle.

pureelectricvehicle;framedesign;loadingdegree;methodofreverberation-raymatrix

2016-01-13

国家重点基础研究发展计划(973计划)资助项目(2010CB328002)；国家自然科学基金资助项目(51475152)

U463.82

10.3969/j.issn.1004-132X.2016.23.021

陈毅强，男，1991年生。湖南大学机械与运载工程学院硕士研究生。主要研究方向为电动汽车车身结构正向设计方法与结构优化。刘子建(通信作者)，男，1953年生。湖南大学机械与运载工程学院教授、博士研究生导师。