阀体焊接机器人运动性能分析

许 勇 程 浩 章 兵 王春燕 吴永博 曹银冬

上海工程技术大学，上海,201620



阀体焊接机器人运动性能分析

许 勇 程 浩 章 兵 王春燕 吴永博 曹银冬

上海工程技术大学，上海,201620

基于弗莱那-雪列(Frenet-Serret)矢量理论，获得了离散焊点处的切向、法向和次法向矢量，据此可求得焊枪-焊点间的相对位姿。基于变位机-机器人主从运动链末端的耦合约束关系，提出以船型焊为最佳焊位时的协同焊接运动学模型及参数求解流程。在求解焊接机器人工作空间的基础上，依据球形手腕六关节串联机器人处于奇异位形的几何条件，归纳得出焊接机器人的10种独立的奇异位形。协同焊接阀体密封面的运动仿真和现场试验表明，该变位机-机器人焊接系统能够平稳、准确地完成预期焊接任务，证实了提出的协同焊接运动学模型及参数求解方法正确可行。

协同焊接；变位机；主从运动链；船型焊

0 引言

随着焊接自动化进程的不断加快和质量指标的日趋严格，采用机器人-变位机或多机器人协同焊接，可使得工作空间更大、灵活度更高、速度更快，更易规避奇异位形，更适应复杂焊缝曲线，获得更好焊接姿态及降低焊接变形[1]。近年来，国内外学者对多机器人(包括机器人-变位机)系统协同运动规划进行了大量研究，主要工作集中在优化焊缝施焊顺序、主从/非主从运动轨迹规划、避碰轨迹规划等方面[1-10]。

在多机器人协同焊接运动规划的研究文献中，机器人位姿变换矩阵中的元素多被表示为系统D-H参数[11](各坐标轴间夹角或距离)的组合，难以直接用来确定焊缝位姿(待焊点序号，焊缝倾角、转角、偏角等)和求解焊枪工作姿态，而且求得的系统正/逆向运动学参数亦为关于结构参数的函数而非关于时间的函数，物理意义不够明确、直观。

本文以机器人和变位机协同作业的自动焊接工作站为研究对象,基于曲线论中的弗莱那-雪列(Frenet-Serret)矢量[9]概念，由焊缝曲线参数方程求得离散化的待焊点位姿，且获得的焊点位姿矩阵元素和后续求得的系统运动学正/逆解参数均为时间变量的函数，其物理意义明确，便于运动控制建模；基于主从运动链末端的耦合约束关系，提出以船型焊为最佳焊位时的协同焊接运动学模型及参数求解流程；依据球形手腕六关节串联机器人处于奇异位形的几何条件，归纳得出焊接机器人的10种独立的奇异位形；最后通过阀体密封面空间椭圆焊缝的焊接作业仿真和现场试验，对提出的协同焊接运动模型及参数求解方法进行验证。

1 离散焊点位姿求解

管道阀门是电力、石化、城市供排水管线中极其关键的流体控制装置。在阀体加工过程必不可少的密封面堆焊中，人工焊接的劳动强度大、操作难度高，且焊接精度差、焊后预留耐磨层不均匀。图1为机器人焊接阀体内壁密封面示意图，其中阀体内壁密封面焊缝已加粗显示。

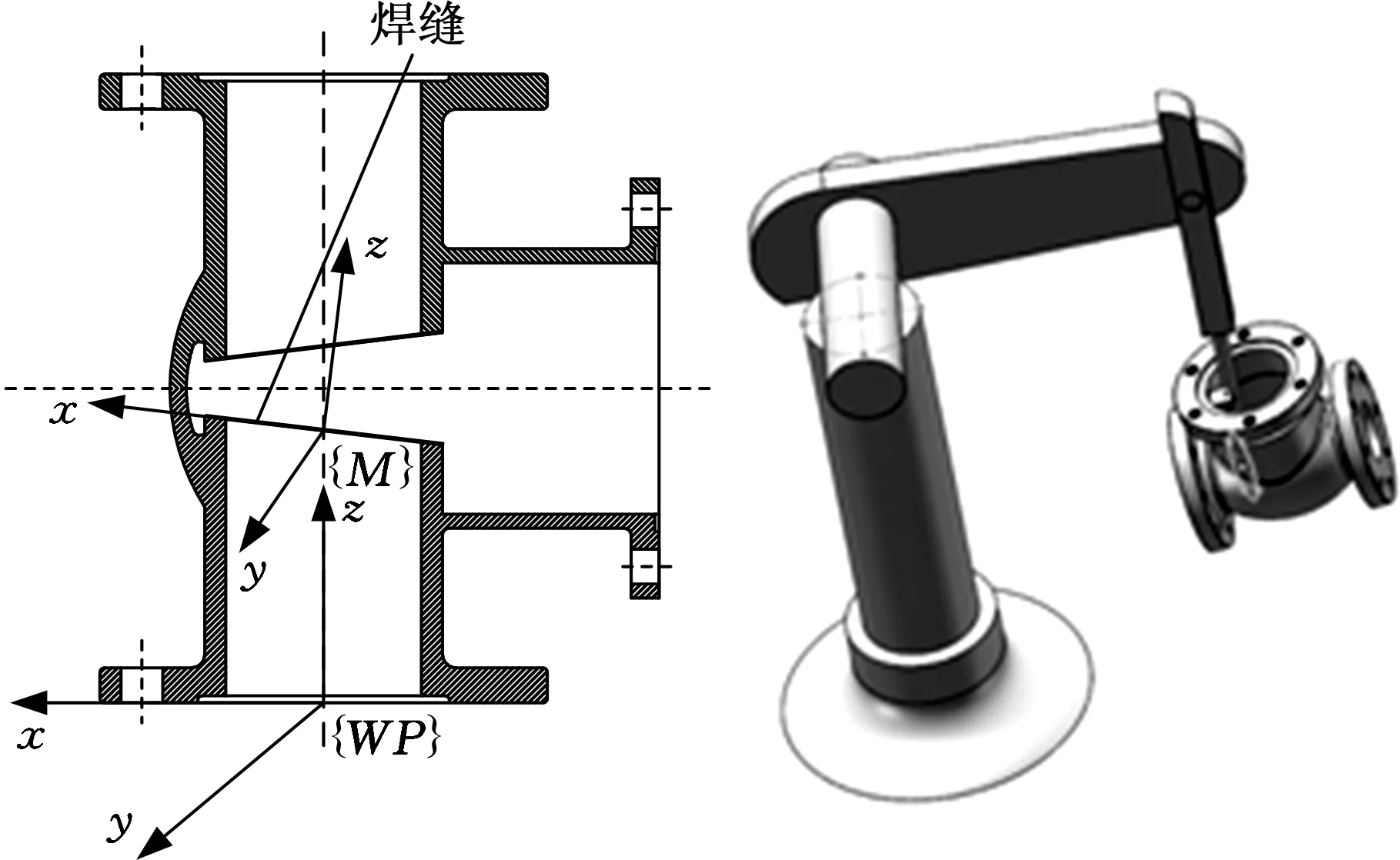
(a)阀体工件及焊缝坐标系 (b)阀体密封面焊接示意图图1 阀体内壁密封面焊接示意图

本文中阀体内壁密封面焊缝为空间椭圆曲线，其参数方程(时间t单位为s，各位移分量单位为mm，下同)为

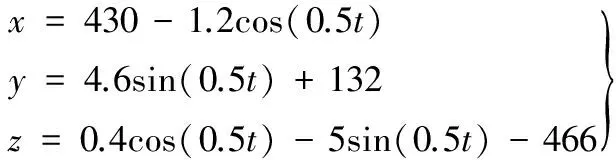
(1)

机器人焊枪的工作姿态由焊枪、焊点坐标轴间所夹的工作角、行走角来描述，且焊枪工作姿态可由焊点姿态经简单变换后得到[6]，因此焊缝中待焊点位姿信息提取是实现机器人协同焊接作业的基础。但只有将焊缝曲线离散化，才能得到密集的离散点。

如图1所示，{WP}为工件坐标系，{M}为待焊点坐标系。待焊点M(x0,y0,z0)是空间椭圆焊缝在时间t=t0时的一点，在该点建立待焊点坐标系如下：令焊缝曲线在焊点M(x0,y0,z0)处的切向为焊点坐标系的x轴，焊点处的外法线方向为待焊点坐标系z轴，由右手法则确定y轴。

本文基于曲线论中的弗莱纳-雪列矢量理论来定义复杂焊缝曲线中离散焊点的位姿。根据弗莱纳-雪列矢量理论，由式(1)中焊缝曲线的参数方程可求得待焊点坐标系相对于工件坐标系的位姿变换矩阵为

(2)

ex=(exx,exy,exz)=(-sin0.83t,cos0.83t,0)

ey=ez×ex=(eyx,eyy,eyz)=

(exzezy-exyezz,exxezz-exzezx,exyezx-exxezy)

ez=(ezx,ezy,ezz)=(-cos0.83t,sin0.83t,1)

p=(px,py,pz)=(430-1.2cos0.5t,4.6sin0.5t+

132,0.4cos0.5t-5sin0.5t-466)

其中ex、ey、ez分别为离散焊点相对于工件的单位切向矢量、法向矢量和次法向矢量[9]，p为焊点相对于工件的位置矢量，均为时间t的函数。

2 变位机-机器人协同焊接运动学建模

2.1 自动焊接工作站系统构型

本文研究的阀体自动焊接工作站系统总体方案如图2所示，该焊接工作站主要由一台二自由度旋倾变位机和一台六自由度球形手腕串联机器人组成，且旋倾变位机的倾斜、旋转转轴分别命名为机器人第7轴、第8轴。{W}为世界坐标系，{R}为机器人基坐标系，{H}为焊枪末端坐标系，{P}为变位机基坐标系，{D}为变位机工作台坐标系。

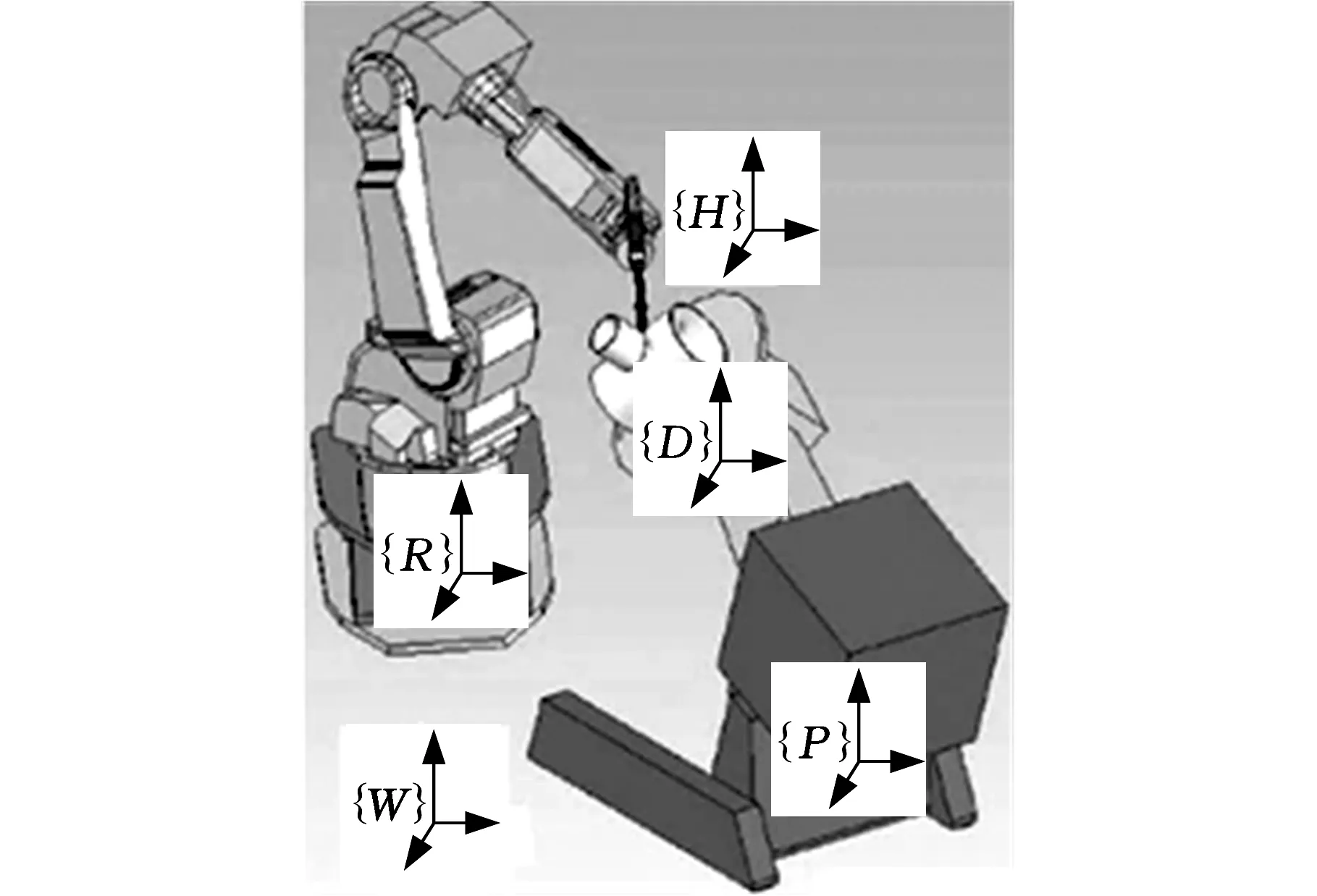
图2 变位机-机器人自动焊接工作站系统构型

按照上述坐标系定义，本文给出焊接工作站中变位机-机器人系统的D-H参数[11]如表1所示。

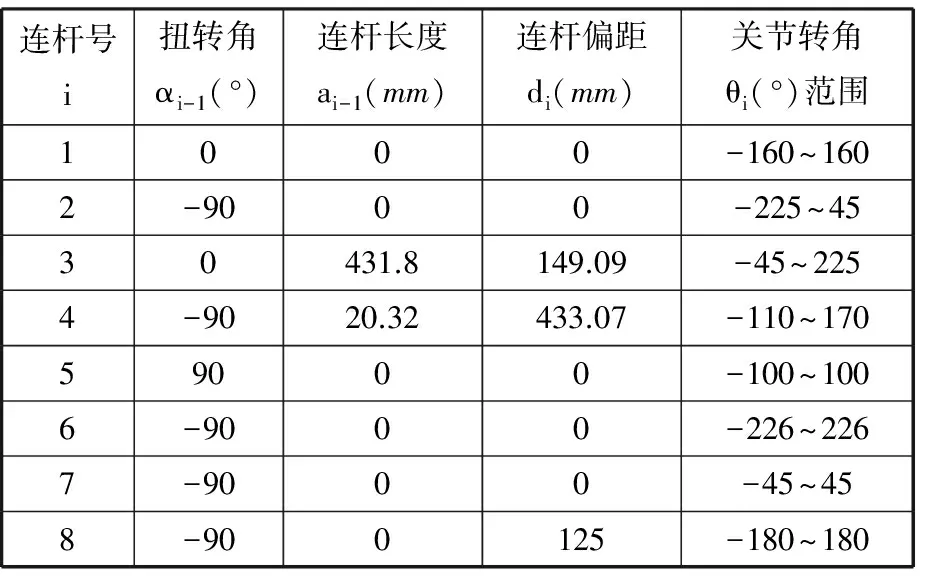
表1 变位机-机器人系统D-H参数

机器人-变位机协同焊接的实现源自于两条开式运动链的耦合：一条为夹持焊件的变位机的“基座-工作台-焊缝”主运动链，使焊缝离散点依次更替并调整到最佳焊接位姿；另一条为焊接机器人的“基座-法兰盘-焊枪”从运动链，该运动链末端按照一定的焊接工艺要求跟踪变位机上的当前焊缝离散点。在协同焊接过程中，这两条开式运动链必然耦合为一条闭环运动链。

2.2 变位机-机器人主从运动链耦合关系方程

机器人、变位机系统要实现协同焊接，必须满足如下运动约束：①焊缝位姿满足最佳焊位要求。当变位机主运动链驱动焊件，使其焊缝上待焊点始终处于船型焊或平焊位姿(待焊点的切向量水平而法向量与重力反向)时，能够获得较优的焊接品质、提高焊接速度[10]。②焊枪工作位姿一定。焊接过程中，机器人从运动链的焊枪应始终以恒定的工作位姿来跟踪变位机主运动链末端的焊缝离散点。③主从运动链末端耦合。协同焊接过程中，主从运动链应通过末端坐标系重合来耦合成一个闭环运动链。

本文以图2所示的机器人和变位机协调船型焊为例，提出变位机-机器人主从运动链耦合关系方程如下：

(3)

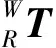
式(3)等号左边反映了变位机主运动链中，焊枪末端坐标系经变位机相对于世界坐标系的运动变换；式(3)等号右边反映了机器人从运动链中，焊枪末端坐标系经机器人相对于世界坐标系的运动变换。

为方便求取变位机和机器人的运动学正逆解，可以将式(3)改写为如下式组合：

(4)

(5)

式(4)即机器人的正运动学方程，用来求解机器人第6轴相对于机器人基坐标系的位姿；式(5)即变位机的正运动学方程，用来求解变位机上焊点相对于世界坐标系的位姿。二自由度旋倾变位机和六自由度球形手腕串联机器人运动学正逆解的具体求解方法可参考文献[9,11]，此处不再赘述。

2.3 变位机-机器人协同焊接运动学参数求解

为了与旋倾运动的变位机实现协同焊接，机器人必须实时追踪变位机工作台上的焊缝待焊点。基于式(3)～式(5)，本文提出协同焊接运动学参数求解流程如下：①求解焊接特定焊缝过程中的变位机关节角θ7、θ8[9]，获得变位机运动学逆解；②将θ7、θ8代回式(5)中，求出待焊点坐标系经变位机相对于世界坐标系的齐次变换矩阵，获得变位机运动学正解；③由式(4)求出机器人第6轴坐标系相对于机器人基坐标系的齐次变换矩阵，获得机器人运动学正解；④由球形手腕串联机器人的解析逆解表达式[11]求出机器人6个关节角θ1～θ6，获得机器人运动学逆解。

3 机器人奇异位形求解

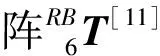
由雅可比矩阵行列式为0时机器人处于奇异位形的定义[12]，本文推导得出球形手腕六关节串联机器人处于奇异位形的几何条件如下：

(1)θ5=0°即sinθ5=0，表示第4和第6转动副共轴，即z4、z6共轴；

(2)θ3=90°即cosθ3=0，表示第2、3、4轴3个轴线z2、z3、z4共面；

(3)a23cosθ2-s44sin(θ2+θ3)=0，表示机器人手腕参考点o4落于由z1及z2确定的平面上。其中，skk表示zk轴上的偏距，aij表示第i和第j运动副之间的法线杆长，下同。

上述3个几何条件可分解为以下10种独立的奇异位形(图4)：

(1)sinθ5=0，cosθ2=0，如图4a所示，此时机器人位形特点为大臂上举，小臂倾斜，第4、第6轴共线；

(2)sinθ4=sinθ5=0，如图4b所示，此时的几何特点除第4、6两轴共轴外，第3、5两轴平行；

(3)sinθ5=0，s22sinθ4-cosθ4cosθ3a23=0，如图4c所示，此时的几何特点是轴4和轴6共线，第5轴线与o1o3直线相交；

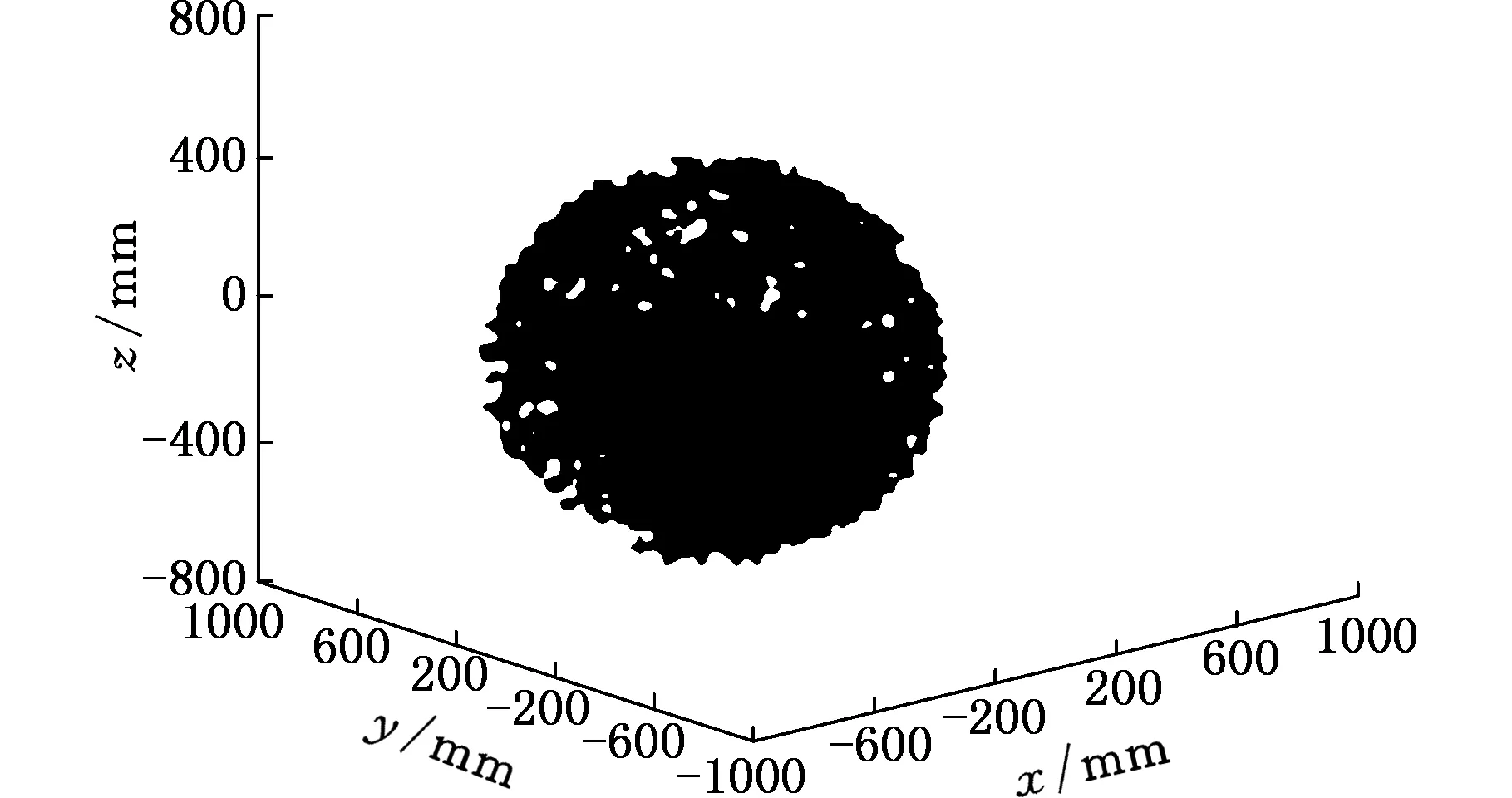
(a)三维工作空间

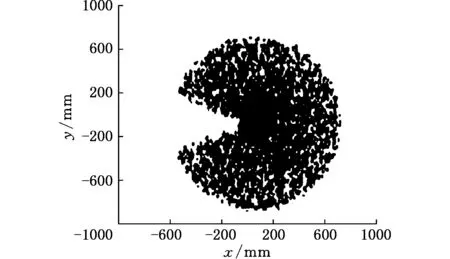
(b)oxy平面投影

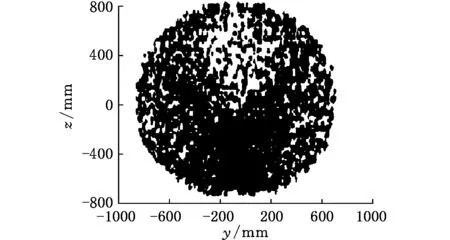
(c)oyz平面投影图3 焊接机器人工作空间

(4)当θ3=-90°时，cosθ3=0, 如图4d所示，此时的几何特点是大小臂伸直；

(5)当a23cosθ2-s44sin(θ2+θ3)=0时, 如图4e所示，此时的几何特点是手腕中心点o4落在由第1和第2轴确定的平面上；

(6)同时存在sinθ5=sinθ4=0及s22sinθ4-sinθ4sinθ3a23=0的情况, 如图4f所示,此时几何上的特点是大小臂以及末杆等3段成一直线；

(7)同时存在sinθ5=cosθ2=0和cosθ3=0的情况， 如图4g所示，此时的几何特点是大小臂及末杆3段成一直线并上举，但轴5不平行轴3；

(8)同时存在sinθ5=sinθ1=cosθ2=0及s22sinθ4-cosθ4cosθ3a23=0的情况，如图4h所示，此时的几何特点是大小臂及末杆成一直线上举，6条轴线共面；

(9)仅有条件sinθ5=0，即仅有4、6共轴，如图4i所示；

(10)同时存在sinθ5=0，sinθ4=sin(θ2+θ3)=0，如图4j所示，此时的几何特点是第4、第6轴共线，轴线z5平行轴线z3，而且小臂在垂直位置。

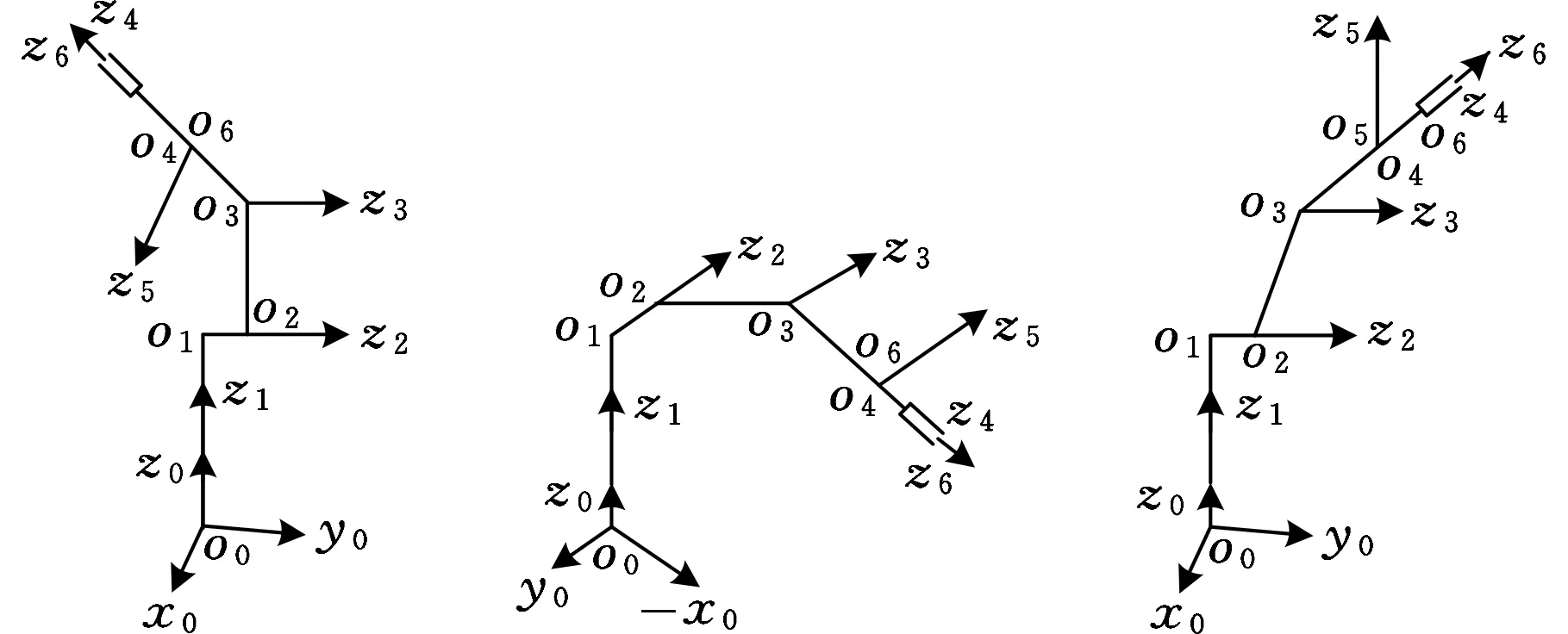
(a) (b) (c)

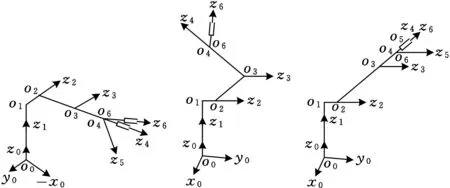
(d) (e) (f)

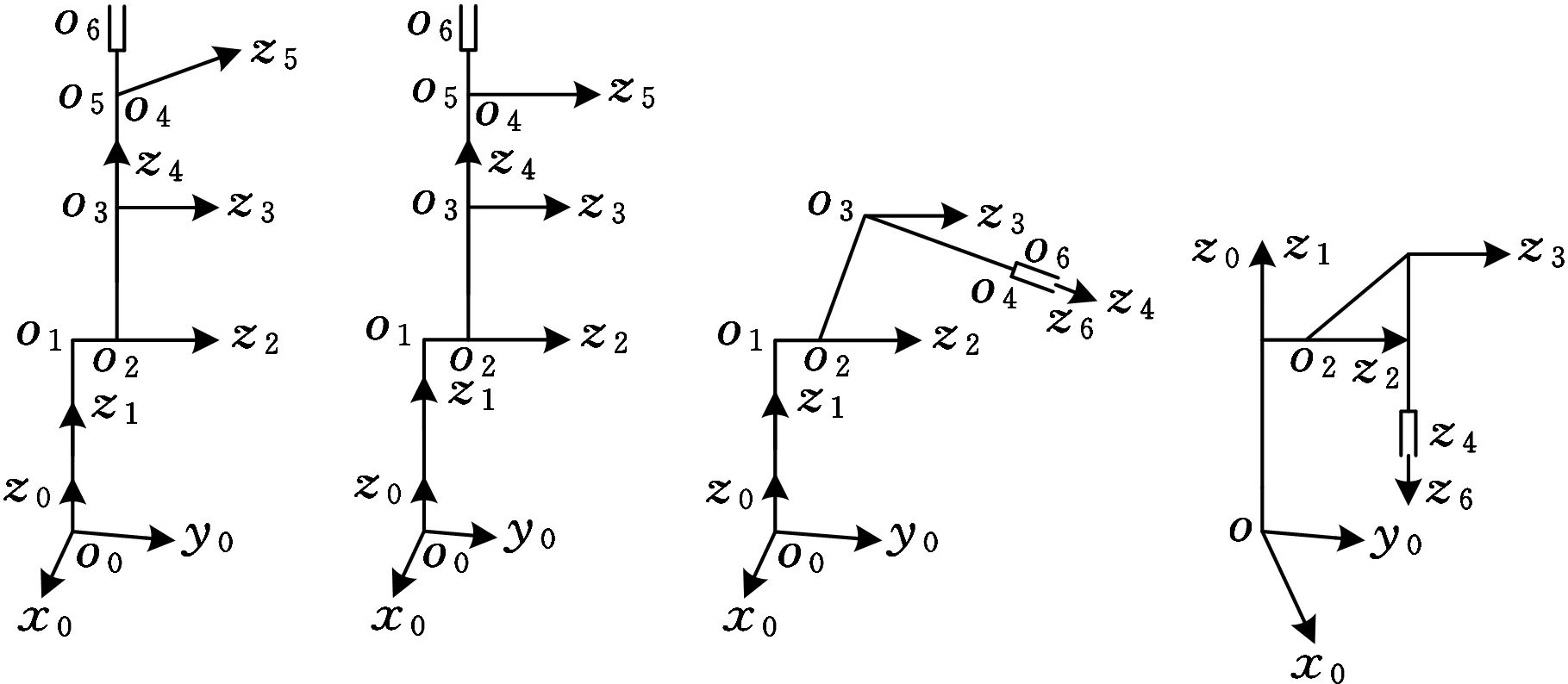
(g) (h) (i) (j)图4 焊接机器人奇异位形

4 阀体密封面协同焊接运动仿真

4.1 协同焊接过程虚拟仿真

在焊接过程中，为保证焊缝始终处于成形良好的位置，要求焊枪相对焊缝始终保持船型位姿[6](即焊枪末端与焊缝待焊点坐标系的z轴重合)不变。本文以焊枪-焊点间的船型相对位姿为约束，在UG虚拟设计环境中进行了阀体密封面机器人-变位机(含阀体工件)系统的协同焊接仿真，部分仿真截图见图5。虚拟仿真过程中测得的机器人关节角θ1～θ6以及焊枪末端轨迹曲线分别见图6、图7。由图6、图7可知，协同焊接过程中机器人关节转角均在合理工作范围内，变位机做匀速旋倾运动，机器人关节转角平滑、周期性变化，共同确保焊枪末端平稳追踪阀体内壁的空间椭圆焊缝。

4.2 极限焊点处机器人位姿求解

(a) (b)

(c) (d)图5 机器人-变位机协同焊接仿真

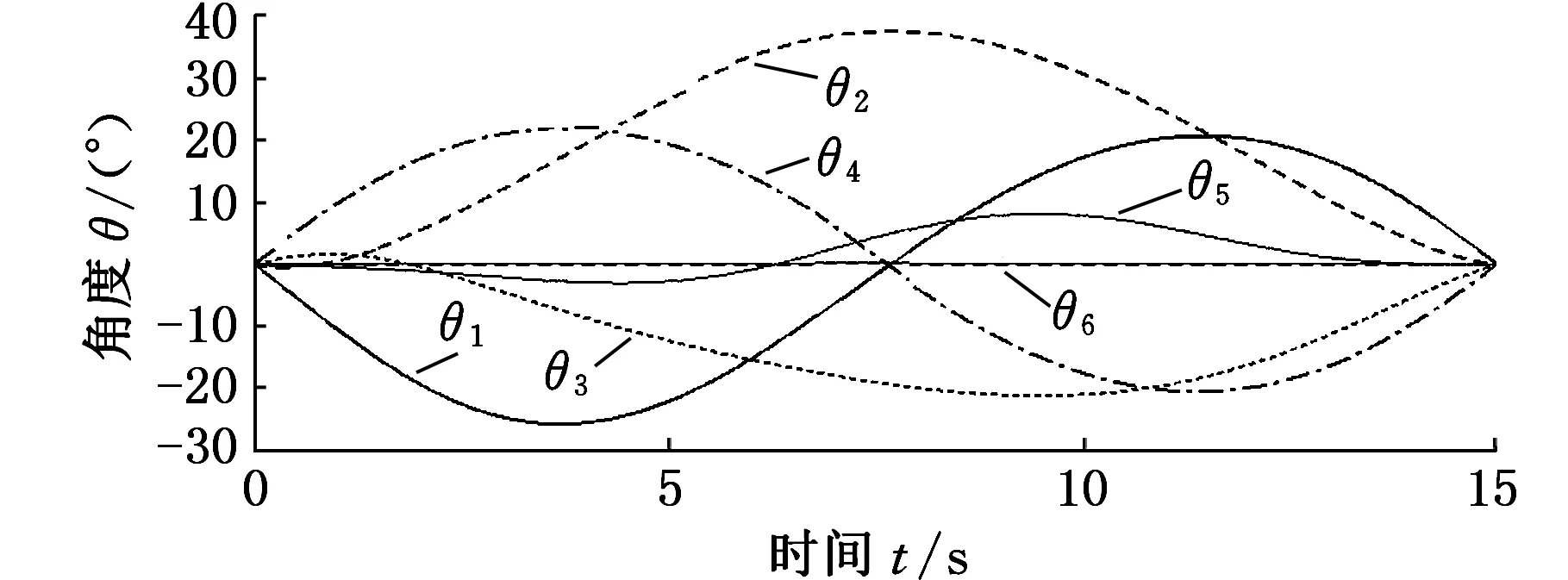
图6 协同焊接过程中机器人各关节角θi变化曲线

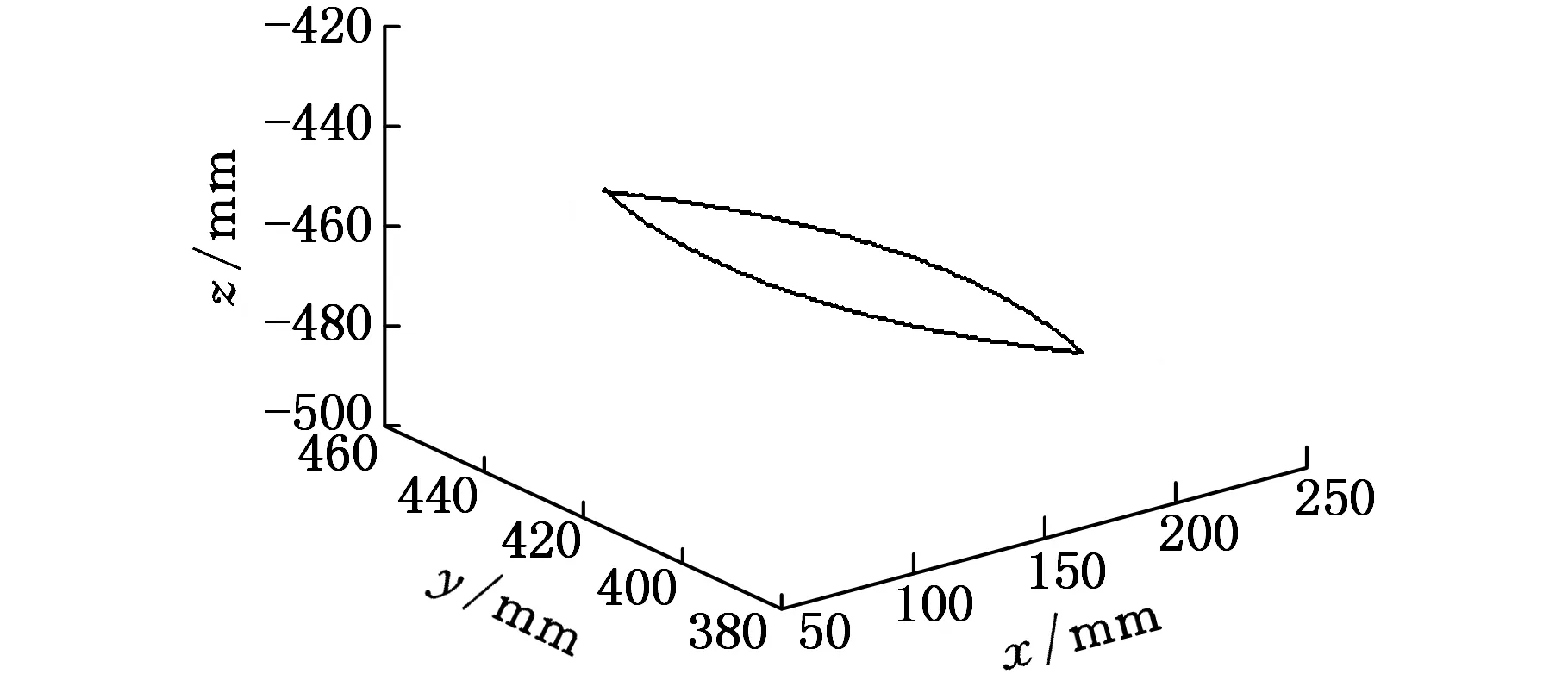
图7 协同焊接过程中的焊枪末端轨迹

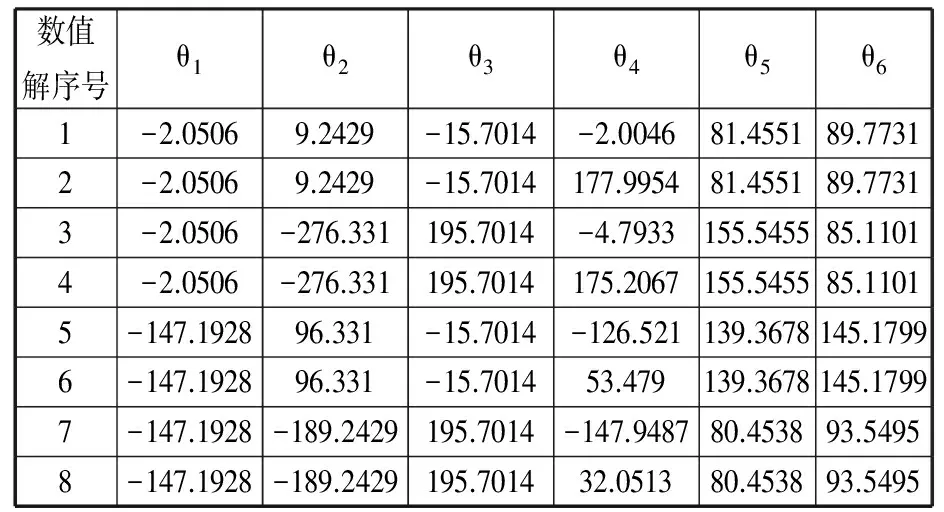
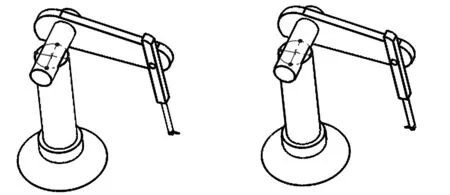
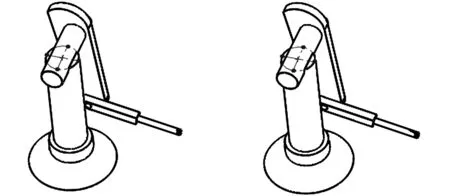
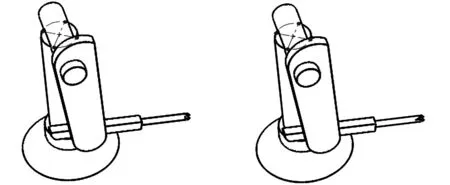
首先在UG虚拟设计环境中，对阀体内壁密封面上的多个焊点处进行焊枪干涉检验，获得了不发生实体干涉的阀体和焊枪的尺寸范围。然后按照2.3节提出的协同焊接运动学参数求解流程，在MATLAB编程环境中，对焊接极限焊点时的机器人关节角进行数值求解。在此仅列出焊接图8所示椭圆焊缝的最低焊点时，所求得的机器人关节角数值解，如表2所示。与表2中各组解一一对应的机器人位姿如图9所示。

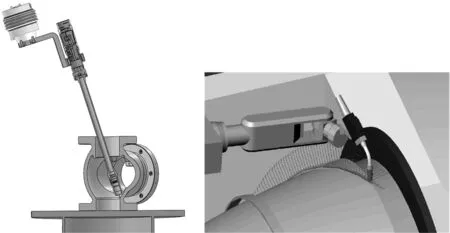
(a)最低焊点干涉检验 (b)最低焊点焊接示意图图8 最低焊点处焊枪干涉检验

表2 焊接最低焊点时的机器人关节角数值解 (°)

(a) (b)

(c) (d)

(e) (f)

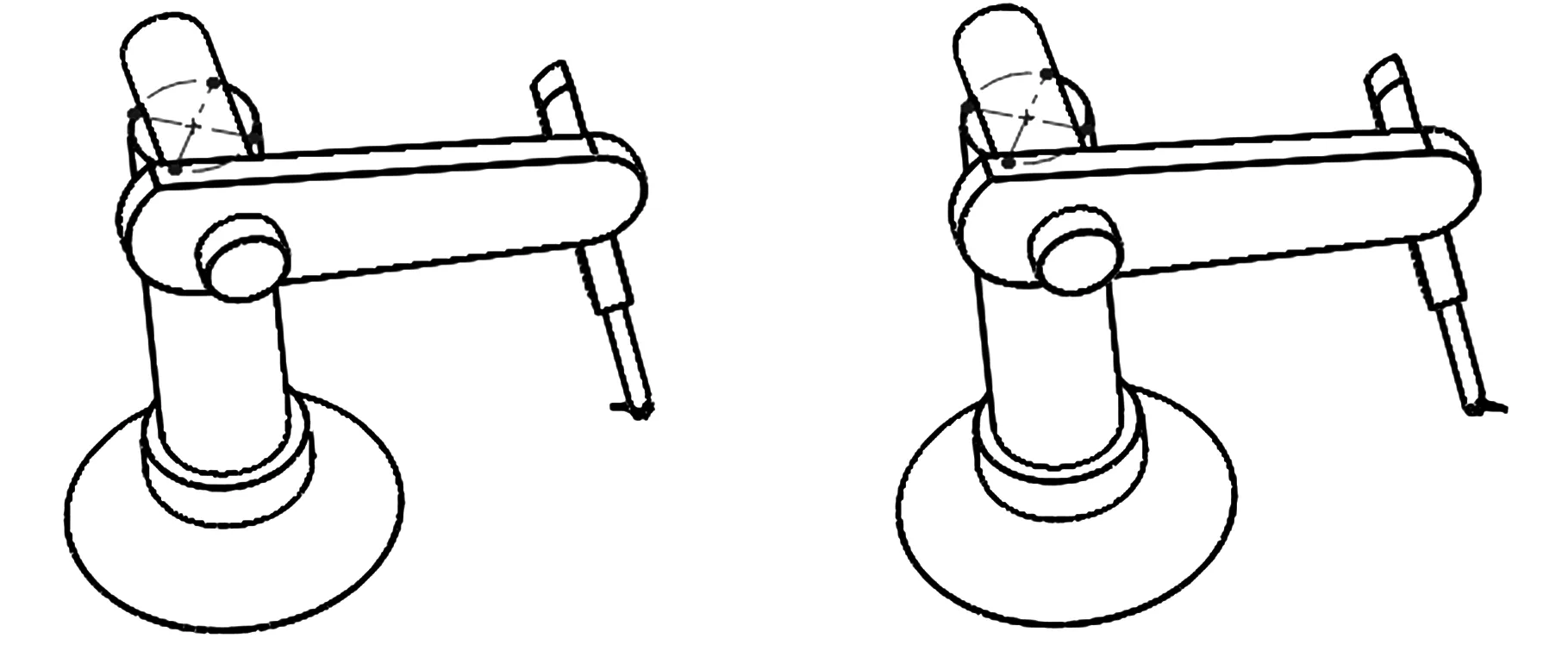
(g) (h)图9 焊接最低焊点时的多种机器人位姿

5 阀体内壁密封面焊接试验

(1)试验要求。①采用耐磨焊丝，多道多层椭圆轨迹堆焊；②焊后机加工预留2 mm耐磨层；③阀体材质为碳钢；④机器人型号为FANUC M-20iA；⑤变位机为RT型；⑥堆焊直径范围为150～800 mm；⑦ 阀口至堆焊口距离为200～230 mm。

(2)主要工艺参数。①单条焊缝总长度440 mm；②焊接速度7 mm/s；③焊接两层，单层厚度为2 mm；④干伸长18 mm；⑤焊枪工作角(焊枪与侧板的夹角)为22°；⑥焊枪行走角(焊枪与焊缝的夹角)为90°；⑦送丝速度5 m/min；⑧起弧/收弧时间6 s；⑨机器人变换位置时间20s；⑧总焊接时间：125.7×2+20+6=277.4 s。

(3)试验结果。①焊枪与焊缝能够很好贴合，焊接过程平稳，焊缝轨迹为平滑椭圆曲线；②使用脉冲焊接模式飞溅小、电弧稳定、焊缝成形美观；③工件深度大于200 mm、密封面锥度大于45°时，标准焊枪无法焊接；④工件直径小于150 mm时，无法使用电弧跟踪和接触寻位功能。

协同焊接试验的部分照片见图10。

(a)焊接过程照片 (b)密封面焊缝照片图10 阀体密封面焊接试验

6 结语

本文提出了基于弗莱那-雪列矢量理论的离散焊点位姿及焊枪位姿的求解方法；基于变位机-机器人主从运动链末端的耦合约束关系，提出以船型焊为最佳焊位时的协同焊接运动学模型及参数求解流程；求解了焊接机器人工作空间，并依据球形手腕六关节串联机器人处于奇异位形的几何条件，归纳得出焊接机器人的10种独立的奇异位形。

阀体内壁密封面协同焊接作业的运动仿真和现场试验表明：协同焊接过程中机器人关节角周期性变化、平滑无突变；焊枪末端点轨迹拟合出精确的空间椭圆曲线，表明焊枪相对焊缝始终保持船型位姿、焊枪末端能够实时平稳地追踪到阀体内壁的椭圆焊缝并与其以较高精度贴合。

上述结果证实了本文提出的协调焊接运动学模型及其参数求解方法正确可行，从而为开发协同焊接机器人工作站及离线编程系统奠定了较为坚实的理论基础。

[1] 何广忠.基于焊接位置数学模型的变位机逆运动学算法[J].机械工程学报，2006，42(6)：86-91. He Guangzhong. Inverse Kinematics of 2R Positioner Based on Welding Postion Representation[J]. Chinese Journal of Mechanical Engineering, 2006,42(6)：86-91.

[2] 康艳君.焊接机器人运动学规划及机器人-变位机的运动仿真[D]：南京：河海大学，2005.

[3] 唐创奇，孟正大.焊接机器人与变位机协调运动的实现[J].工业控制计算机，2008(1):47-49. Tang Chuangqi, Meng Zhengda. Realization of Coordinated Motion of Welding Robot and Positioner[J]. Industrial Control Computer，2008(1):47-49.

[4] 宋学志.焊接变位机的运动规划与到位精度研究[D].武汉：华中科技大学，2007.

[5] Li Kai, Zhang Ting. Seam Tracking Control System of Intelligent Mobile Welding Robot [C]//Proceedings of the Second International Conference on Intelligent Networks and Intelligent Systems. Tianjin，2009:269-272.

[6] 张铁.基于运动链末端耦合与解耦的机器人协同焊接算法[J].华南理工大学学报，2013，41(11)：56-61. Zhang Tie. Robot Cooperative Welding Algorithm Based on Coupling and Decoupling of Kinematic Chains [J]. Journal of South China University of Technology，2013，41(11)：56-61.

[7] Caccavale F. Six-DOF Impedance Control of Dual-arm Cooperative Manipulators [J].IEEE/ASME Transactions on Mechatronics，2012，13(5):576-586.

[8] Gan Yahui. Kinematic Cooperation Analysis and Trajectory Teaching in Multiple Robots System for Welding [C]//Proceedings of IEEE 16th Confer-ence on Emerging Technologies & Factory Automation (ETFA). Toulouse，2012:1-8.

[9] 翟敬梅.双机器人协同焊接的轨迹优化[J].焊接学报，2015，36(1)：91-95. Zhai Jingmei. Trajectory Optimization of Dual-robot Coordinated Welding[J]. Transactions of the China Welding Institution，2015，36(1)：91-95.

[10] 罗辉.焊接机器人与变位机的协调运动规划[D].哈尔滨：哈尔滨工业大学，2013.

[11] 蔡自兴.机器人学[M].北京：清华大学出版社，2004.

[12] 黄真.并联机器人机构学理论及控制[M] .北京：机械工业出版社，1997.

(编辑 苏卫国)

Motion Performance Analyses of Valve Welding Robots

Xu Yong Cheng Hao Zhang Bing Wang Chunyan Wu Yongbo Cao Yindong

Shanghai University of Engineering Science,Shanghai,201620

The tangential vectors, normal vectors and auxiliary normal vectors of the discrete solder joints were solved based on Frenet-Serret’s vector theory. Thus the relative positions and orientations between welding point and welding torch will be derived more easily. Based on the coupling constraint relationship between the ends of the active positioner kinematic chain and the driven robot kinematic chain, the coordinated welding kinematic model and the corresponding parameter solving process were presented for the optimum ship-welding position. On the basis of solving the working space of the welding robot, according to the geometric conditions of the singular positions for the spherical wrist 6-joint series robot, 10 independent singular positions of the welding robot were obtained. The motion simulation and field tests of the robot-positioner coordinated welding operation show that the system may smoothly and accurately complete the coordinated welding tasks of valve sealing surface. These results confirm that the proposed kinematic model and parameter solving process are correct and feasible.

coordinated welding; welding positioner; active and driven kinematic chain; ship welding

2015-11-12

TG409;TP242.3

10.3969/j.issn.1004-132X.2016.23.003

许 勇,男,1973年生。上海工程技术大学机械工程学院副教授。研究方向为机器人机构学。发表论文30余篇。程 浩，男,1994年生。上海工程技术大学机械工程学院硕士研究生。章 兵，男,1992年生。上海工程技术大学机械工程学院硕士研究生。王春燕，女,1992年生。上海工程技术大学机械工程学院硕士研究生。吴永博，男,1995年生。上海工程技术大学机械工程学院本科生。曹银冬，男,1994年生。上海工程技术大学机械工程学院硕士研究生。