平行连杆式操作机悬挂系统刚度与阻尼参数研究
杨晓波 刘艳妍 杨 晋 高俊峰
1.兰州交通大学,兰州,7300702.兰州兰石能源装备工程研究院有限公司,兰州,730050
平行连杆式操作机悬挂系统刚度与阻尼参数研究
杨晓波1刘艳妍1杨 晋1高俊峰2
1.兰州交通大学,兰州,7300702.兰州兰石能源装备工程研究院有限公司,兰州,730050
为合理设计操作机悬挂系统的缓冲装置以减小惯性冲击的影响,针对平行连杆式锻造操作机,简化了设备模型,分析了制动工况下悬挂系统各杆件的受力状态和运动规律,并利用牛顿-欧拉法综合各杆件的动力学分析,建立了悬挂系统在制动时的动力学模型,提出了缓冲装置刚度及阻尼参数确定的思路。以300 kN锻造操作机为例,在MATLAB中求解操作机悬挂系统动力学微分方程,分析了缓冲刚度、阻尼对吊杆摆角、钳杆质心运动规律的影响。结果表明,利用牛顿-欧拉法建立模型确定缓冲刚度与阻尼参数的方法是可行的与合理的,从而为平行连杆式操作机悬挂系统缓冲装置的刚度与阻尼设计提供了理论依据。
锻造操作机;悬挂系统;缓冲装置;牛顿-欧拉方程;刚度;阻尼
0 引言
重载锻造操作机是制造产业链中实现锻造机械化与自动化的重要辅助设备之一, 用于夹持锻件配合压机完成各种锻造工艺动作[1]。锻压车间中使用重载锻造操作机与锻造设备协同工作,可以大幅度提高产业制造能力、锻件制造精度、材料利用率,缩短生产周期,降低工业能耗[2]。重载锻造操作机悬挂系统是连接操作机行走部与夹持部的核心部件,其结构形式主要有摆动杠杆式与平行连杆式[3]。
锻造操作机悬挂系统缓冲装置主要用于保证钳杆夹持锻件在锻压、启动、制动工况时的稳定性[4]。相对于锻压工况和大车启动工况,操作机为实现其操控快速响应,大车行走部在短时间内快速制动,对于大载荷、大惯量的悬挂系统,缓冲装置将承受更大的非连续性单向冲击载荷。同时,悬挂系统空间结构复杂、杆件数目多、缓冲装置受力状态复杂,使系统的动力学特征难以求解。因此,缓冲装置设计方案的确定对重载锻造操作机悬挂系统设计具有重要意义。文献[5]基于钳杆平升降运动,建立拉格朗日动力学方程,分析了摆杆式吊挂系统中缓冲装置与系统振动的关系,为设计摆杆式吊挂系统提供了新依据。文献[6]利用旋量理论对一种新型操作机悬挂系统的自由度及运动原理进行了分析,并采用1∶20的锻造操作机实验模型对其理论进行验证。文献[7]采用修正的Grübler-Kutzbach 公式计算了DDS锻造操作机悬挂系统中并联机构的自由度,并首次对该机构进行了运动学分析,为这种锻造操作机的运动学控制提供了理论依据。文献[8]提出了通过组合旋量理论和降维系统动力学来研究操作机悬挂系统动力学特性。文献[9]研究了操作机在拔长初期夹持锻件大范围顺应运动时的动力学行为,并分析了悬挂系统中缓冲装置的非线性特性。文献[10]在ADAMS中建立锻造操作机三维模型,依据实际工况添加约束和载荷,得到锻造操作机典型工况的动态性能仿真结果。
国内外学者针对不同形式锻造操作机悬挂系统的力学行为与动态响应规律等问题进行了深入研究,但多数学者在针对特定工况研究悬挂缓冲装置时并未将操作机制动工况作为极端载荷条件;对悬挂系统运动学和动力学分析时,多数将缓冲缸作为二力杆或直接将其与操作机液压系统联合建立方程,并未深入考虑缓冲装置刚度及阻尼特性对悬挂系统的影响。
因此,本文以平行连杆式操作机悬挂系统为例,针对制动工况建立悬挂系统动力学模型,分析悬挂系统杆件的受力状态和运动规律,研究缓冲装置刚度、阻尼与系统振动的关系,为合理设计锻造操作机悬挂系统缓冲装置提供理论依据。
1 悬挂系统物理模型
1.1 平行连杆式操作机悬挂系统
如图1a所示,平行连杆式悬挂系统由多个平行四边形机构及其附属杆件串并联混合而成,可确保操作机运动时机构不出现运动盲点而使缓冲装置工作失效[11-12]。其中,后转臂1、连杆2、缓冲缸3、提升缸5、前转臂6、前吊杆8在钳杆7、俯仰缸4两侧呈对称分布。将空间机构投影至钳杆中心线所在平面,如图1b所示,平面机构中提升缸LJ与连杆HI共同实现钳杆的升降运动,俯仰缸FE和缓冲缸MN分别实现钳杆的俯仰运动和缓冲运动。
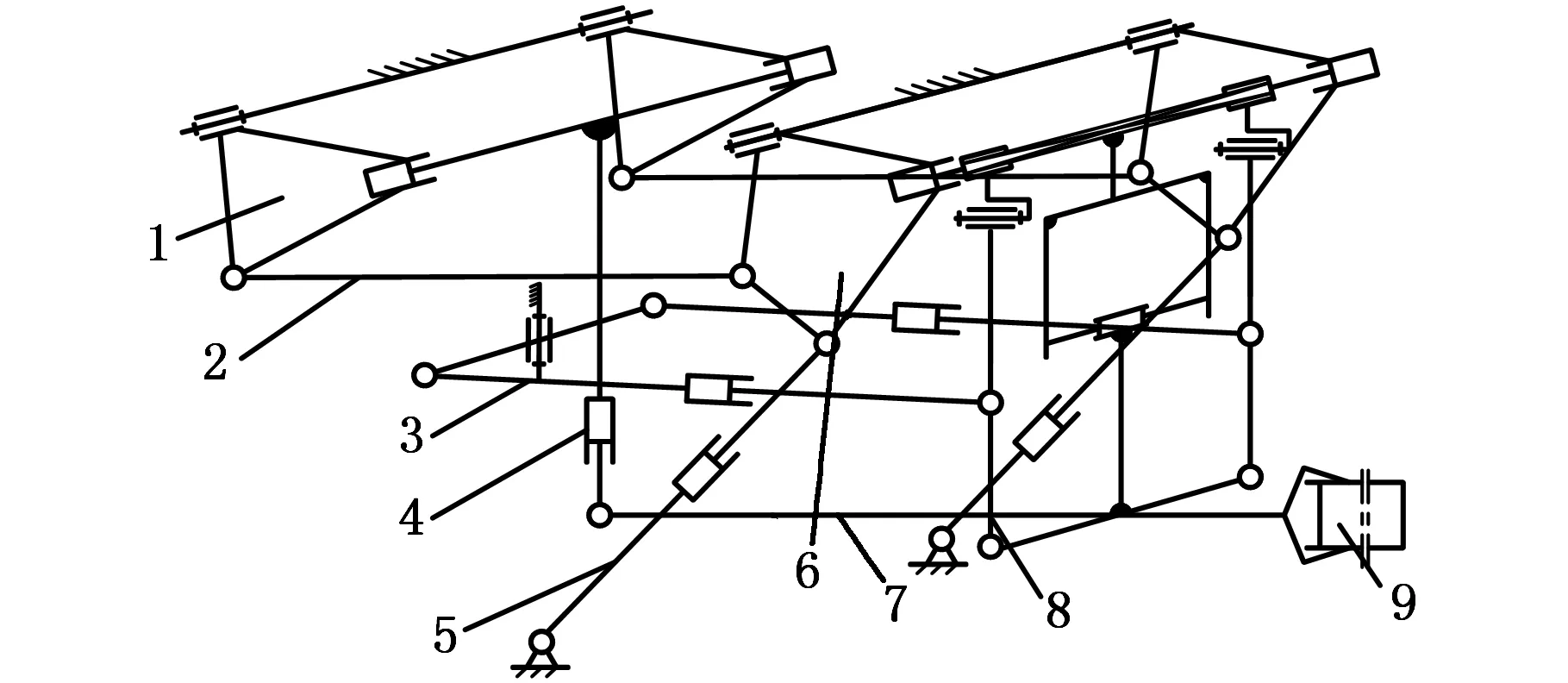
1.后转臂 2.连杆 3.缓冲缸 4.俯仰缸 5.提升缸 6.前转臂 7.钳杆 8.前吊杆 9.锻件(a)悬挂空间轴测图
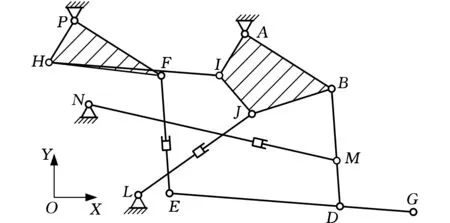
(b)悬挂机构投影图图1 悬挂机构模型
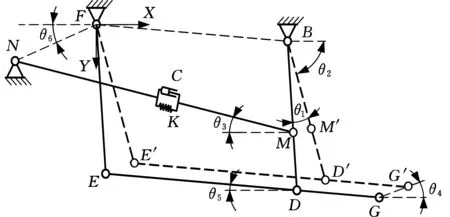
图2 悬挂机构简化模型
1.2 简化模型分析
制动工况下,图1b中悬挂机构的提升缸LJ和俯仰缸FE处于闭锁状态,因此可用连杆代替,缓冲缸MN处于工作状态。点A与车体固接,提升缸LJ没有位移输出,所以前转臂ABJI固定不动。后转臂中点P与车体固接,并通过连杆HI与前转臂ABJI连接,同样不运动。又因机构中点B、F不运动,所以悬挂机构可以简化为图2。
图2中,为便于建立悬挂系统动力学模型,将各杆件视为刚体,其质量用集中质量代替;为着重分析悬挂系统杆件承受制动载荷时缓冲装置对系统振动的影响,忽略杆件关节处摩擦影响;液压缸和蓄能器组成缓冲缸MN,起到缓冲与减振作用,并利用刚度和阻尼等效缓冲缸的功能[12]。以点F为原点,停车方向为X轴方向,重力方向为Y轴方向,建立坐标系。其中,θ1为摆动后的前吊杆与初始位置夹角;θ2为初始位置时的前吊杆与水平方向夹角;θ3为缓冲缸与水平方向夹角;θ4为钳杆平移方向与水平方向夹角;θ5为钳杆与水平方向夹角;θ6为缓冲缸末端和原点连线与水平方向夹角。
2 悬挂系统动力学模型
常用动力学建模方法有牛顿-欧拉方程法、达朗贝尔原理、拉格朗日方程法、凯恩方程法等,每种方法各有特点,适合不同的动力学系统建模[13-14]。本文针对制动工况,依据平行连杆式悬挂的特点,选用牛顿-欧拉方程法建立模型。
2.1 各杆件受力分析
(1)缓冲缸由液压缸和蓄能器组成,液压缸传递惯性冲击,蓄能器吸收振动。以缓冲缸为研究对象,受力情况如图3所示,图中,C、K分别为缓冲缸阻尼、刚度。依据力平衡可得如下关系。
X轴平衡:
FNX=-FMX
(1)
Y轴平衡:
FNY=-mMNg+FMY
(2)
N点取矩:
(3)
FMX=(FC+FK)cosθ3
FMY=(FC+FK)sinθ3
式中,FC为缓冲阻尼力;FK为缓冲刚度力;vMN为缓冲缸速度;lMN为缓冲缸杆原长;MMN为缓冲缸惯性力矩。
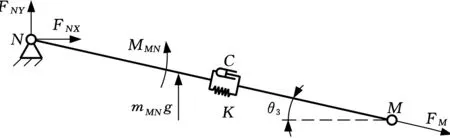
图3 缓冲缸受力分析
(2)以前吊杆作为研究对象,受力情况如图4a所示,根据受力平衡可得如下关系。
X轴平衡:
(4)
Y轴平衡:
(5)
B点取矩:
(6)
式中,lBD为前吊杆杆长;MBD为前吊杆惯性力矩。
(3)以俯仰缸作为研究对象,受力情况如图4b所示,根据受力平衡可得如下关系。
X轴平衡:
(7)
Y轴平衡:
(8)
F点取矩:
(9)
式中,lFE为俯仰缸杆长;MFE为俯仰缸惯性力矩。
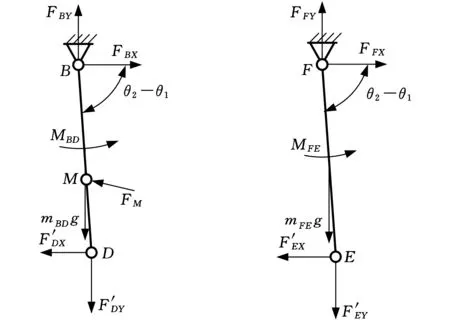
(a)前吊杆 (b)俯仰缸图4 前吊杆和俯仰缸受力分析
(4)以钳杆为研究对象,受力情况如图5所示,根据受力平衡可得如下关系。
X轴平衡:
FEX+FDX=FAX
(10)
Y轴平衡:
FEY+FDY-mEGg=FAY
(11)
E点取矩:
-FDYlEDcosθ5-FDXlEDsinθ5+mEGglEGcosθ5=
-FAXlEGsinθ5-FAYlEGcosθ5
(12)
D点取矩:
FEXlEDsinθ5+FEYlEDcosθ5+mEGglDGcosθ5=
-FAXlDGsinθ5-FAYLDGcosθ5
(13)
FAX=FAcosθ4FAY=FAsinθ4
式中,FA为钳杆惯性力;lEG为钳杆杆长。
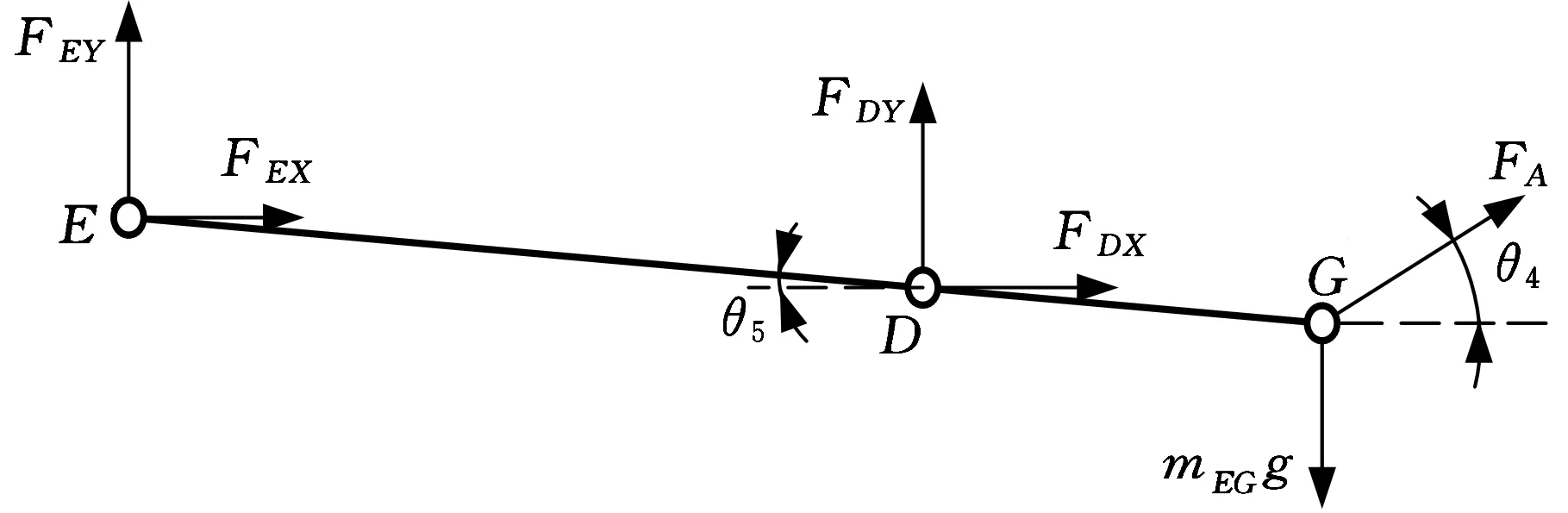
图5 钳杆受力分析
2.2 建立动力学方程
联合式(9)与式(12)可得
(14)
(15)
联合式(6)与式(13)可得
(16)
(17)
将式(15)、式(17)代入式(11)可得悬挂系统动力学微分方程:
(18)
C1=lEDcosθ5lFEsin(θ2-θ1)-lEDsinθ5lFEcos(θ2-θ1)
C2=lEDcosθ5lBDsin(θ2-θ1)-lBDcos(θ2-θ1)lEDsinθ5
D1=(-mlBDcosθ4lDGsinθ5-mEDlBDcosθ4lDGcosθ5)·
LFEsin(θ2-θ1)-JFElEDsinθ5
D2=-mEGgLDGcosθ5LFEsin(θ2-θ1)-
D3=(mEGlBDcosθ4lEGsinθ5+mEGlBDsinθ4lEGcosθ5)·
lBDsin(θ2-θ1)-JBDlBMsin(θ2-θ1)
D4=mEGglEGcosθ5lBDsin(θ2-θ1)+
(-FMXlBMsin(θ2-θ1)+FMYlBMcos(θ2-θ1)-
缓冲刚度和缓冲阻尼两参数对系统振动影响可由式(18)中前吊杆与初始位置夹角θ1的变化规律反映;通过建立杆件之间的位置矢量方程,可以明确缓冲参数对钳杆质心运动的影响规律;综合两缓冲参数对系统振动影响可确定平行连杆式悬挂缓冲装置的刚度与阻尼的设计方案。
3 实例分析
以300 kN操作机为例,给定钳杆夹持锻件时机构各杆件间位置配合关系及质量参数,以制动速度vb=195 mm/s为悬挂系统动力学微分方程初始条件,在MATLAB中利用四阶Runge-Kutta法求解动力学模型。
3.1 悬挂系统缓冲刚度与阻尼确定
制动工况中,缓冲装置主要保证钳杆质心的位置精度与快速衰减系统所受到的惯性冲击。因此合理确定缓冲刚度和阻尼,改善悬挂机构各杆件的受力状态,减小钳杆振幅,缩短振动衰减时间是系统缓冲装置设计的关键。
悬挂系统动力学方程中刚度和阻尼两参数分别对系统的振动影响如图6、图7所示。随着缓冲装置的阻尼和刚度增大,前吊杆的摆角及钳杆质心的水平与垂直位移量逐渐减小并趋于稳定。
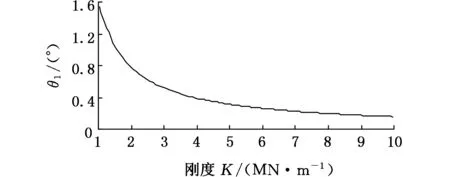
(a)前吊杆夹角变化曲线
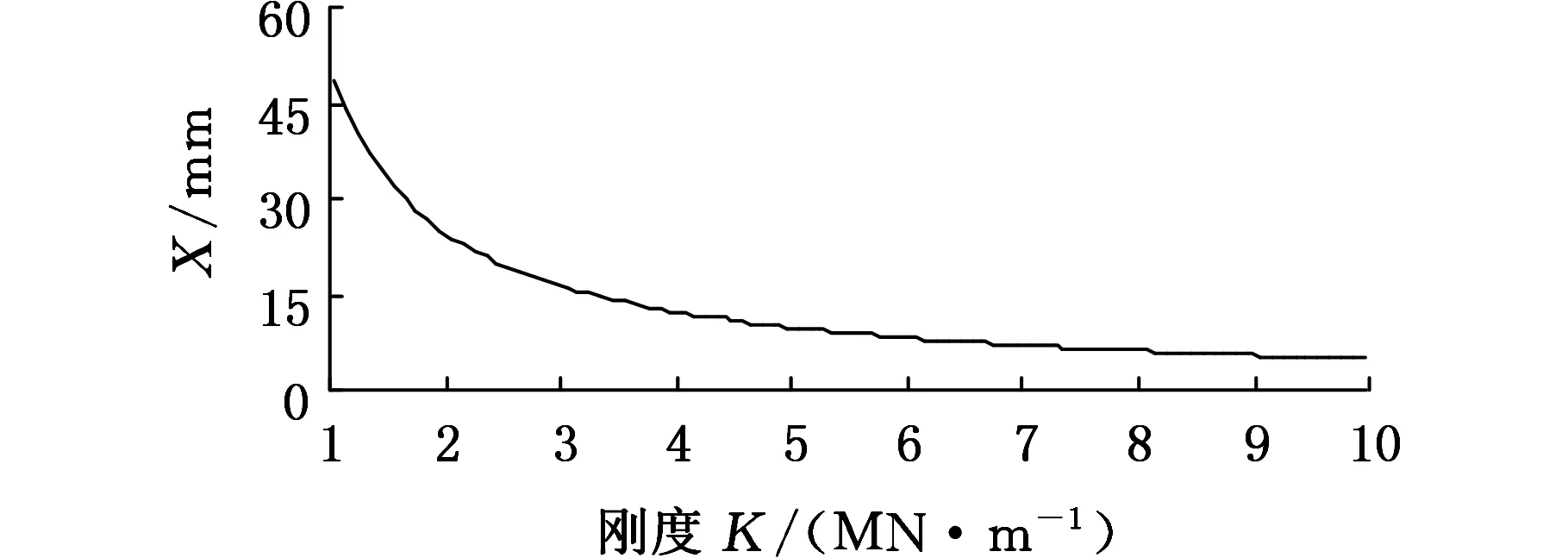
(b)钳杆质心水平变化曲线
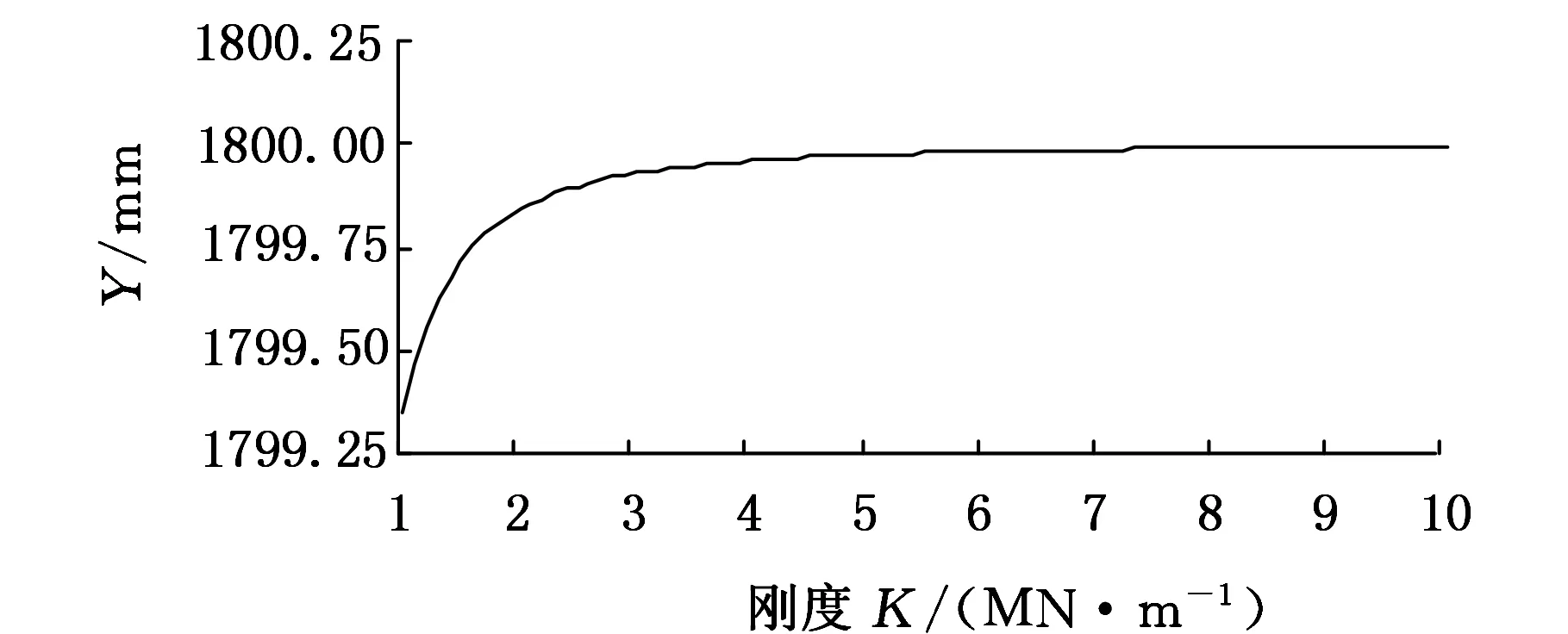
(c)钳杆质心垂直变化曲线图6 刚度K对系统振动的影响
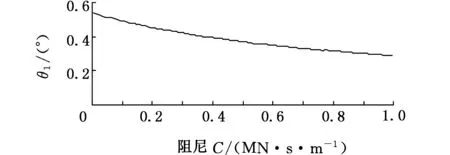
(a)前吊杆夹角变化曲线
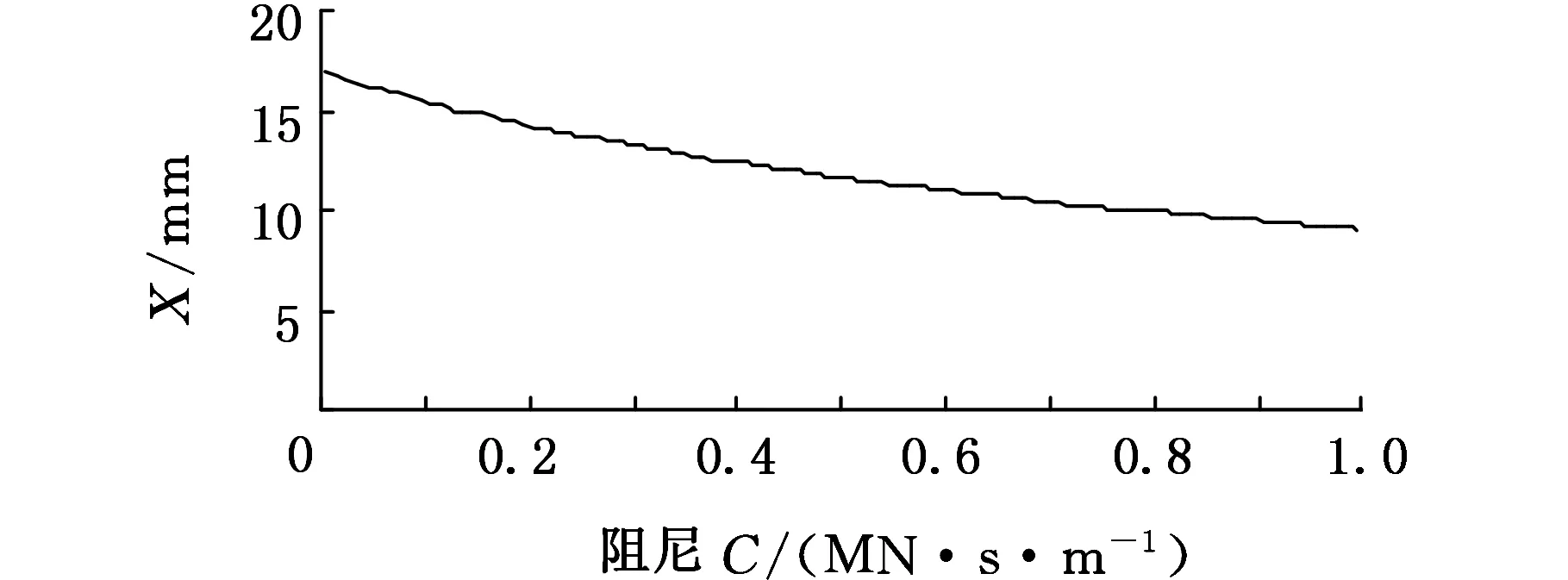
(b)钳杆质心水平变化曲线
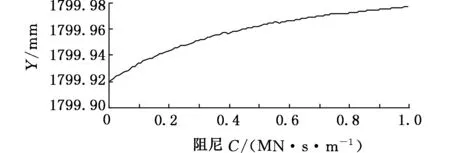
(c)钳杆质心垂直变化曲线图7 阻尼C对系统振动的影响
操作机运动时,钳杆质心水平振幅相对于垂直方向变化范围较大,且对操作机正常工作产生影响。因此,操作机制动时应以钳杆质心最小水平位移变化量确定缓冲装置的刚度及阻尼更为合理。由图6b可知,当设定阻尼C为零时,随着刚度K的逐渐增大,钳杆质心水平变化范围逐渐减小并且趋于稳定,缓冲刚度的选择范围为7.4~8.6 MN/m;由图7b看出,同理设定刚度K为零时,随阻尼C的增大,钳杆质心水平位移变化范围逐渐减小并且趋于稳定,可确定缓冲阻尼范围为0.8~0.95 MN·s/m。悬挂系统中缓冲装置的刚度、阻尼在制动工况下共同作用,依据系统中工件质心水平位移变化量为最优目标原则,在选定的刚度和阻尼区间内,同时对两参数进行穷举搜索,经运算可得刚度K=8.4 MN/m,阻尼C=0.95 MN·s/m。
3.2 缓冲装置对比分析
操作机原设计方案中悬挂系统采用缓冲刚度K=3.6 MN/m、阻尼C=0.55 MN·s/m的缓冲装置,吊挂系统的振动曲线如图8所示,钳杆质心在水平方向最大振幅范围为-8~12 mm,垂向最大振幅为0.5mm,系统3.5s左右趋于稳定。虽然悬挂系统中使用原方案设计的缓冲装置使系统承受制动惯性冲击时呈现收敛特性,可减小钳杆在制动时受到的惯性冲击,但是系统水平摆动幅度依旧超出操作机控制精度要求范围,并且系统振动衰减时间过长。
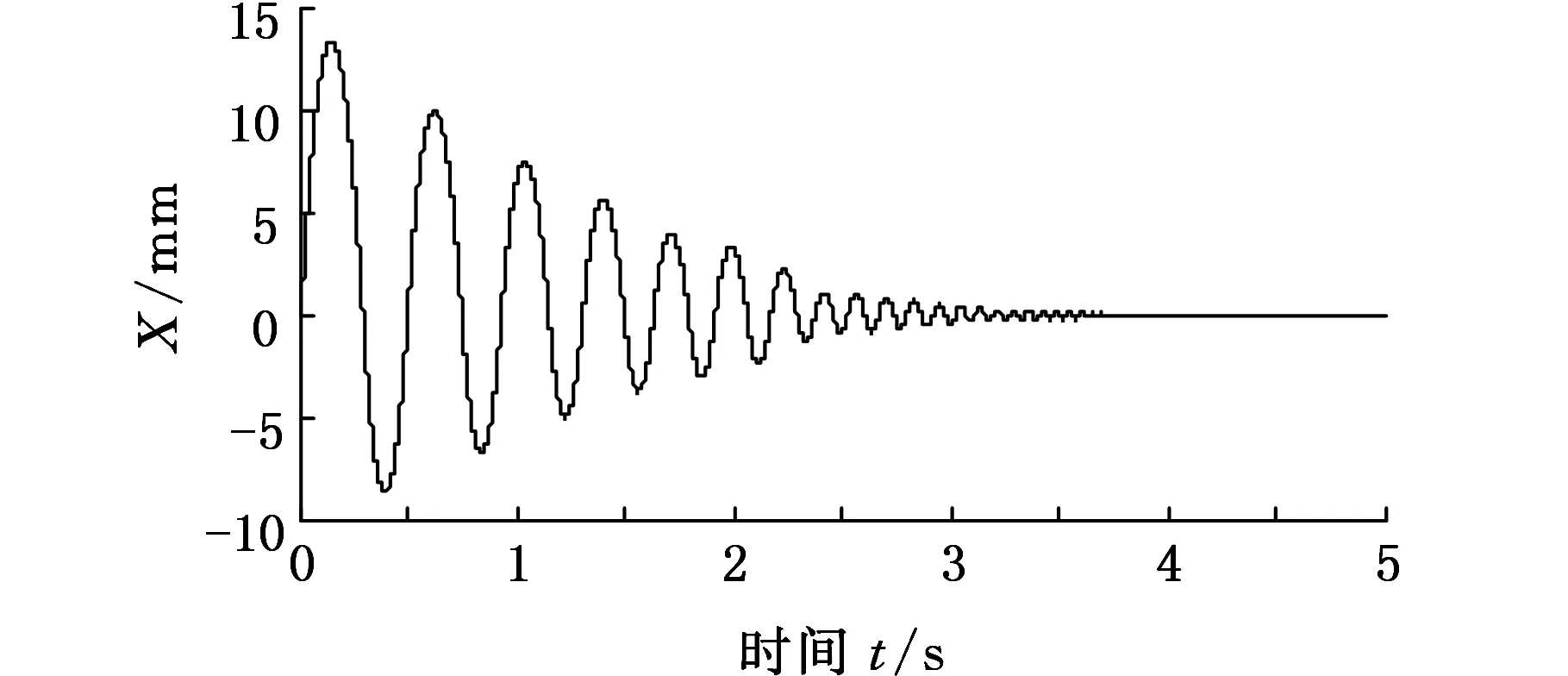
(a)水平方向
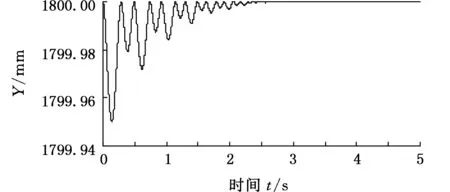
(b)垂直方向图8 原方案对钳杆质心变化的影响
若悬挂系统中缓冲装置给定从系统动力学获得的刚度与阻尼值,即K=8.4 MN/m,C=0.95 MN·s/m,则吊挂系统的振动情况如图9所示,钳杆质心在水平方向最大振幅范围为-3.8~5.6 mm,钳杆质心垂向几乎不产生位移变化,最大振幅仅为0.08 mm,系统1.5 s左右趋于平稳。
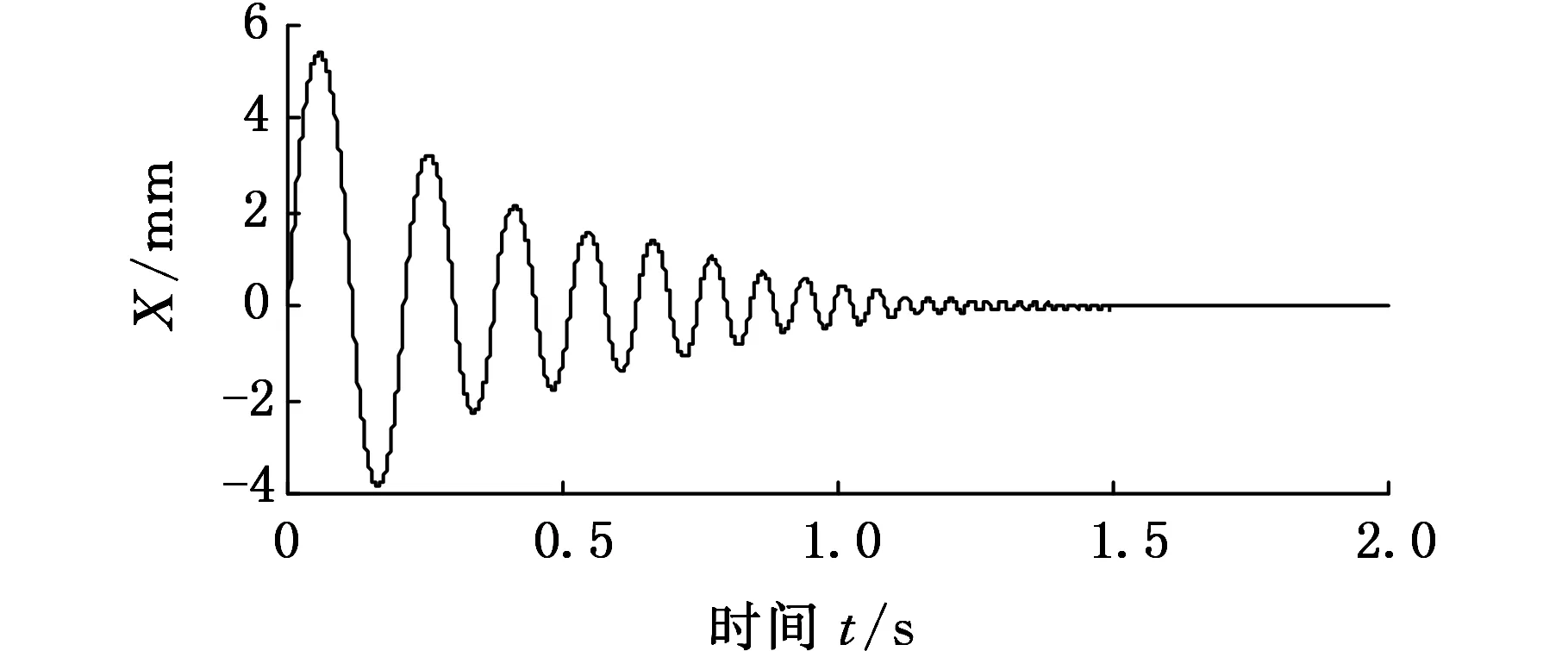
(a)水平方向
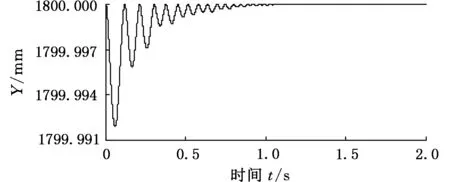
(b)垂直方向图9 新方案对钳杆质心变化的影响
相对于原设计方案,重新确定的缓冲装置参数明显改善了悬挂系统中钳杆质心在水平与垂直方向的位移变化,缩短了系统振动的时间,增加了操作机对其位置精度控制的稳定性,保证了设备在恶劣工况下的可靠性。
4 结论
(1)针对制动工况分析了平行连杆式重载锻造操作机悬挂模型中杆件的受力和运动状态,建立了制动工况下悬挂系统的动力学微分方程,为研究操作机缓冲刚度与阻尼参数提供了条件。
(2)通过求解操作机悬挂系统动力微分方程,分析了刚度、阻尼对系统振动的影响,研究了确定缓冲装置刚度及阻尼的思路,为合理设计缓冲装置提供了依据。
(3)以300 kN重载锻造操作机为例,采用MATLAB求解动力学微分方程,分析了制动工况下刚度与阻尼对悬挂系统的吊杆摆角、钳杆质心的影响,验证了缓冲装置刚度及阻尼确定方法的正确性。
[1] 杨文玉,孟富明. 锻造操作机顺应性能评价与优化方法[J].机械工程学报,2010, 46(23):121-127. Yang Wenyu, Meng Fuming. Evaluating and Optimization Method of Forging Manipulator Compli-ance[J]. Journal of Mechanical Engineering, 2010, 46(23):121-127.
[2] Chen G, Wang H, Zhao K, et al. Modular Calculation of the Jacobian Matrix and Its Application to the Performance Analyses of a Forging Robot [J]. Advanced Robotics, 2009, 23(10):164-179.
[3] Xu Yundou. Inverse Dynamics and Internal Forces of the Redundantly Actuated Parallel Manipulators [J]. Mechanism and Machine Theory, 2012, 51(11):172-184.
[4] 赵勇,林忠钦,王皓. 重型锻造操作机的操作性能分析[J].机械工程学报,2010, 46(11):69-75. Zhao Yong, Lin Zhongqin, Wang Hao. Manipula-tion Performance Analysis of Heavy Manipulators[J]. Journal of Mechanical Engineering, 2010, 46(11):69-75.
[5] 杨晋,何琪功,同新星. 摆杆式操作机钳杆平升降缓冲刚度与阻尼研究[J]. 振动与冲击,2013, 32(9):105-109. Yang Jin, He Qigong, Tong Xinxing. Buffering Stiffness and Damping in Vertical Lifting and Dropping Movements of the Clamping-bar of an Oscillating-bar Forging Manipulator[J]. Journal of Vibration and Shock, 2013, 32(9):105-109.
[6] Xu Yundou, Liu Yu, Yao Jiantao, et al. Analysis of a Novel Lifting Mechanism for Forging Manipul-ators[J]. Mechanical Engineering Science, 2015, 229(3):528-537.
[7] 许允斗,姚建涛,赵永生. 一种典型DDS锻造操作机运动学分析[J]. 机械工程学报,2012, 48(3):50-56. Xu Yundou, Yao Jiantao, Zhao Yongsheng. Kinematic Analysis of a Typical DDS Forging Manipu-lator[J]. Journal of Mechanical Engineering, 2012, 48(3):50-56.
[8] Ding W H, Deng H, Li Q M, et al. Control-orientated Dynamic Modeling of Forging Manipulators with Multi-closed Kinematic Chains[J]. Robotics and Computer-Integrated Manufacturing, 2014, 30(5):421-431.
[9] 李刚,刘德时. 锻压操作机大范围顺应运动的动力学行为分析[J]. 机械工程学报,2010, 46(11):21-28. Li Gang, Liu Deshi. Dynamic Behavior of the Forging Manipulator under Large Amplitude Compliance Motion[J]. Journal of Mechanical Engineering, 2010, 46(11):21-28.
[10] 李刚,宋三灵,张凯. 基于ADAMS 的重载操作机的动力学仿真[J]. 中国工程机械学报,2010, 8(3):264-268. Li Gang, Song Sanling, Zhang Kai. ADAMS-based Dynamical Simulation on Heavy-duty Manipulators[J]. Chinese Journal of Construction Machinery, 2010, 8(3):264-268.
[11] 许允斗,赵永生. 3种锻造操作机主运动机构受力比较分析[J]. 机械设计,2012, 29(7):38-42. Xu Yundou, Zhao Yongsheng. Force Comparative Analysis of Three Mechanisms of Forging Manipulator[J]. Journal of Machine Design, 2012, 29(7):38-42.
[12] Staicu S. Dynamics of the 6-6 Stewart Parallel Manipulator[J]. Robotics and Computer-Integrated Manufacturing, 2011, 27 (1):212-220.
[13] 杨义勇,金德闻. 机械系统动力学[M]. 北京:清华大学出版社,2009.
[14] Spong M W, Vidyasagar M. Robot Dynamics and Control[M]. New York:Wiley, 2008.
(编辑 王旻玥)
Study on Stiffness and Damping Parameters of Parallel Link-Manipulator’s Suspension System
Yang Xiaobo1Liu Yanyan1Yang Jin1Gao Junfeng2
1.Lanzhou Jiaotong University, Lanzhou, 730070 2.Lanzhou LS Energy Equipment Engineering Research Co., Ltd., Lanzhou, 730050
In order to design a buffer device of forging manipulator’s suspension system rationally to reduce the influences of inertial impacts, aiming at the parallel style forging manipulators, the model of forging manipulator was simplified, the stress states and the motion laws of rods in the suspension system under the braking conditions were analyzed. By using Newton-Eular rule with dynamic analysis of the rods, the suspension system’s dynamics model under braking conditions was constructed and the method of determining parameters such as buffer device’s stiffness and damping was proposed. Using a 300 kN forging manipulator as an example, the dynamics differential equation of the manipulator’s suspension system was solved with MATLAB to analyze the buffering stiffness and damping’s influences on the hanging bar’s swing angle and the motion of clamping bar’s centroid position. The results indicate the feasibility and rationality of determining buffering stiffness and damping using the model constructed with Newton-Eular rule and provide theoretical basis for the stiffness and damping design of the parallel link-manipulator’s suspension system.
forging manipulator; suspension system; buffer device; Newton-Euler equation; stiffness; damping
2016-06-27
国家自然科学基金资助项目(51265022);甘肃省科技计划资助项目(145RJZA187)
TG315.4
10.3969/j.issn.1004-132X.2016.23.002
杨晓波,男,1991年生。兰州交通大学机电学院硕士研究生。主要研究方向为材料成形装备。刘艳妍,女,1964年生。兰州交通大学机电学院教授。杨 晋,男,1962年生。兰州交通大学机电学院教授。高俊峰,男,1961年生。兰州兰石能源装备工程研究院有限公司高级工程师。

