金属橡胶静刚度特性及其力学模型研究

余慧杰 刘文慧 王亚苏

上海理工大学，上海，200093



金属橡胶静刚度特性及其力学模型研究

余慧杰 刘文慧 王亚苏

上海理工大学，上海，200093

对金属橡胶成形机理和静刚度特性影响因素进行分析，运用螺旋弹簧刚度理论建立了金属橡胶微元弹簧理论模型，并根据试验结果对其进行模型修正。通过理论模型与试验的比较，发现理论模型值与试验值较接近，可以较全面地反映金属橡胶静刚度特性，从而为金属橡胶减振器的设计和金属丝工艺参数的确定提供理论依据。

金属橡胶；静刚度特性；力学模型；工艺参数

0 引言

随着现代工业的快速发展，振动、噪声问题越来越突出。消除振动和噪声最有效的方法之一是采用阻尼材料。金属橡胶是一种新型干摩擦阻尼材料，它成形于金属丝的缠绕、编织和压缩，具有金属和橡胶的特性[1]，而且具备阻尼大、吸收冲击能力强、在真空中不挥发、不惧怕辐射环境、耐高低温、耐疲劳老化、寿命长和可以长期保存等优点，在航空航天、尖端武器装备等领域具有非常广阔的应用前景[2-3]。

金属橡胶的力学特性复杂，探究其力学模型是设计金属橡胶减振器的基础。现有的力学模型主要有悬臂梁模型、角锥模型、多孔材料模型等[4]，但这些模型中的物理量含义不明确，或预估参数过多，给金属橡胶的工程应用带来了困难。

本文从金属橡胶内部微观结构出发，将基本单元螺旋卷简化为微元弹簧，应用经典压缩弹簧理论公式，建立金属橡胶微元弹簧力学模型，对影响金属橡胶静刚度特性的主要因素进行试验，对力学模型进行修正，并获得模型参数。

1 力学模型

1.1 微元弹簧力学模型的建立

由金属橡胶的成形机理可知，金属橡胶由很多螺旋卷组成，如图1a所示，可以将这些螺旋卷简化为微元弹簧串联和并联的形式，如图1b所示。每个微元弹簧的刚度与其丝径和中径的大小有关[5-6]：金属橡胶丝径增大，即微元弹簧丝径增大，微元弹簧的刚度增大，使得金属橡胶的刚度增大；金属橡胶螺旋卷直径增大，即微元弹簧中径增大，微元弹簧的刚度减小，使得金属橡胶的刚度减小；当金属橡胶的相对密度增大即单位体积内微元弹簧数量增多时，串联和并联的微元弹簧数量增多，使得金属橡胶的刚度增大[7-9]。故金属橡胶承载由微元弹簧承担，其耗能阻尼是由微元弹簧之间滑移而产生干摩擦，从而消耗大量振动能量而起到的阻尼作用。

(a)微元弹簧单元 (b)微元弹簧串并联图1 金属橡胶简化为微元弹簧单元

根据圆柱压缩弹簧的计算公式[10]，得出单个微元弹簧的载荷Fij与位移x的关系为

(1)

kij=Gd4/(8D3)

式中，Fij为第j层第i个弹簧单元的受力；kij为第j层第i个弹簧单元的刚度系数；d为丝径；D为弹簧中径(金属橡胶中的螺旋卷直径)；G为弹簧切变模量。

假设在高度方向上有m层弹簧，每层内有n个微元弹簧，层内微元弹簧相互并联，层间微元弹簧相互串联[11]。根据弹簧叠加理论，每层内微元弹簧相互并联，其总刚度为

(2)

各层之间弹簧相互串联，其总的等效刚度为[12]

(3)

虽然各微元弹簧的形态各不相同，但总体而言存在一个统计上的平均值，假定以平均值k作为微元弹簧刚度系数kij，kij=k(i=1,2,…,n;j=1,2,…,m),则

(4)

因此，金属橡胶的载荷-位移关系可表示为

(5)

假设金属橡胶材料线匝在三个相互垂直方向上是等概率分布的，则体积为V的金属橡胶内微元弹簧总数量为[13]

(6)

(7)

2 刚度特性

由上述分析可知，金属橡胶的刚度大小与金属橡胶的丝径、螺旋卷直径、相对密度等工艺参数和承载面积、高度等外形参数紧密相关。

由于承载面积、高度等外形参数测量简便，它们对金属橡胶刚度的影响比较直观，所以，在本文中，只给出丝径、螺旋卷直径、相对密度等工艺参数对金属橡胶静态刚度的影响。

为了探究金属橡胶刚度随其影响因素的变化规律，本文采用BOSE ElectroForce 3330多功能试验机对金属橡胶进行分组试验，如图2所示。

(a)多功能材料试验机 (b) 金属橡胶试件 图2 试验机和试件实物照片

将金属橡胶分成三组进行试验，分别研究金属丝丝径、螺旋卷直径、相对密度对金属橡胶刚度的影响。金属橡胶试件的材料选用1Cr18Ni9Ti奥氏体不锈钢丝，其密度ρs=7.85×10-3g/mm3，试件的外形尺寸(外径×内径×高)为10 mm×5 mm×8.5 mm，即金属橡胶承载面积S=58.9 mm3,金属橡胶圆柱的高度H=8.5 mm,加载速率为0.05 mm/s，可视为静态加载。具体参数如表1所示。

表1 金属橡胶试件参数

2.1 金属丝丝径的影响

在1号试件中，对丝径不同、其他参数相同的金属橡胶进行静态压缩试验，得到载荷-位移曲线，见图3。由图3可以看出，随着金属丝丝径的增大，金属橡胶刚度增大，硬特性的增大较明显，其关系可表示为K∝d。

图3 不同丝径下载荷-位移曲线

2.2 螺旋卷直径的影响

在2号试件中，对其他参数相同、螺旋卷直径不同的金属橡胶进行静态压缩试验，得到载荷-位移曲线，见图4。从图4中可以看出，随着螺旋卷直径的增大，金属橡胶刚度减小，且硬特性降低较明显，其关系可表示为K∝1/D。

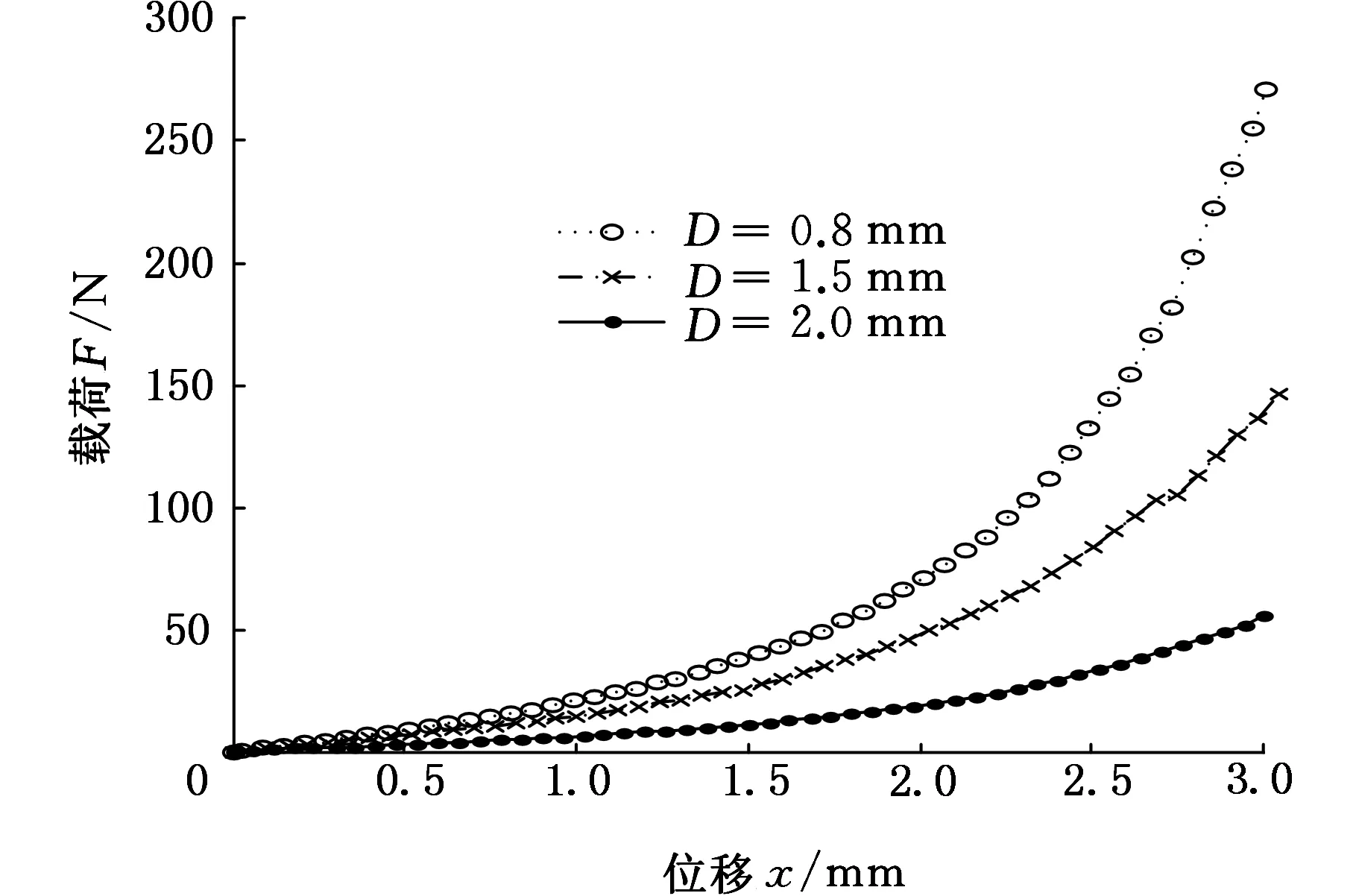
图4 不同螺旋卷直径下载荷-位移曲线

2.3 相对密度的影响

图5 不同相对密度下载荷-位移曲线

由以上三组静态压缩试验可知，金属橡胶的刚度随着金属丝丝径的增大、螺旋卷直径的减小、相对密度的增大而增大，这与微元弹簧得到的力学模型相吻合。另外，当外形尺寸改变时，其对金属橡胶的刚度也有类似的影响。

2.4 微元弹簧力学模型的修正

上述试验都表明金属橡胶的刚度呈现线性—软特性—硬特性的非线性变化特点，但微元弹簧模型得到的刚度力学模型却为线性模型，这与微元弹簧模型为小位移线弹性有关。而试验中，金属橡胶的变形往往是大变形，呈现非线性特性，因此必须对理论模型进行修正。

将线性模型修正为非线性模型常用的方法是将一次函数修正为高次函数。根据试验得到的金属橡胶载荷-位移的非线性关系，在原有微元弹簧力学模型的基础上，将上述金属橡胶载荷-位移关系修正为三次函数，函数中的待定系数可通过试验数据求得。修正后的金属橡胶载荷-位移关系为

(8)

式中,a1、a2、a3为待定系数。

该微元弹簧修正模型可以较直观地反映金属橡胶材料、丝径、螺旋卷直径、相对密度、金属橡胶承载面积以及成形高度对金属橡胶力学特性的影响。

3 参数识别与验证

3.1 参数识别

式(8)中的微元弹簧模型的待定系数需要通过具体试验进行参数识别。本文用静态压缩的试验数据进行模型参数识别。用最小二乘法拟合三次多项式系数，从而确定式(8)中a1、a2、a3的值。

试验所用金属橡胶材料为奥氏体不锈钢1Cr18Ni9Ti，金属丝密度ρs=7.85×10-3g/mm3，金属丝切变模量G=71 GPa,试件的外形尺寸(外径×内径×高)分为:10 mm×5 mm×8.5 mm，10 mm×5 mm×9 mm，10 mm×5 mm×10 mm，14 mm×5 mm×8.5 mm四种。用最小二乘法进行拟合，获得方程的各项系数：a1=0.54，a2=-0.26，a3=0.10，于是得到金属橡胶微元弹簧的修正模型为

(9)

3.2 模型试验验证

为验证上述金属橡胶微元弹簧修正模型的正确性和适用性，另取三种不同参数的金属橡胶样品进行试验，具体参数如表2所示。

表2 金属橡胶试验验证参数

对以上3组金属橡胶进行静态压缩试验，对计算出的理论值进行验证，试验值与理论值对比结果如图6所示。

图6 金属橡胶刚度的模型计算值与试验值对比

由以上试验可知，所建立的金属橡胶微元弹簧修正模型能较好地描述其静态载荷-位移关系与金属丝材料、丝径、螺旋卷直径、相对密度、外形尺寸的变化关系，试验曲线和理论曲线误差很小，所采用的三次多项式可以较准确地描述金属橡胶线性区和软特性区的刚度特性。

从图6中也可以看出，在硬特性区的刚度特性误差较大，这是因为金属橡胶在硬特性区时，各个螺旋卷之间相互挤压、啮合，部分螺旋卷发生塑性变形，此时再将其简化为微元弹簧模型将会引起较大的误差。但在金属橡胶的实际应用中，金属橡胶一般工作在线性和软特性区域，所以建立的金属橡胶微元弹簧模型的半经验方程可以基本满足设计需要，可为金属橡胶减振器的设计、金属丝工艺参数等的确定提供理论依据。

4 结语

在现有金属橡胶力学模型的基础上，通过对金属橡胶成形机理，刚度特性的影响因素，以及细观螺旋卷单元的分析，将金属橡胶中的基本单元螺旋卷简化为微元弹簧，根据弹簧理论，推导金属橡胶载荷-位移关系，并对其进行三次曲线修正，从而建立了金属橡胶微元弹簧理论修正模型。所建立的金属橡胶微元弹簧理论模型直观地反映了金属橡胶静刚度特性(载荷-位移关系)与金属橡胶材料、丝径、螺旋卷直径、相对密度、金属橡胶承载面积、厚度的定量关系，可以较全面地反映金属橡胶静刚度特性，为金属橡胶减振器的设计和金属丝工艺参数的确定提供理论依据。

[1] 姜洪源，敖宏瑞，夏宇宏，等.金属橡胶成形工艺研究及其应用[J]. 机械设计与制造, 2001(2):85-86. Jiang Hongyuan, Ao Hongrui, Xia Yuhong，et al. Metal Rubber Molding Technology Research and Its Application[J]. Mechanical Design and Manufacturing, 2001(2):85-86.

[2] 侯军芳，白鸿柏，李冬伟，等.高低温环境金属橡胶减振器阻尼性能试验研究[J].航空材料学报,2006,26(6):50-54. Hou Junfang, Bai Hongbo, Li Dongwei,et al. At High and Low Temperature Environment Test Research on Metal Rubber Shock Absorber Damping Performance[J]. Journal of Aviation Materials,2006,26(6):50-54.

[3] 赵程，贺跃进，张恒.金属橡胶的应用研究[J].噪声与振动控制,2006,26(5):45-47. Zhao Cheng, He Yuejin, Zhang Heng. The Application of Metal Rubber [J]. Noise and Vibration Control, 2006,26(5):45-47.

[4] Huang M, Dong X, Liu G. 3D Modeling of the Preparation Process of Metal Rubber Material[J]. International Journal of Minerals, Metallurgy, and Materials, 2010, 17(1): 75-79.

[5] Wang Y, Li Z, Liu B, et al. Stiffness Characteristic Comparison between Metal-rubber and Rubber Isolator under Sonic Vibration[J].Journal of Vibroengineering,2014,16(2):645-655.

[6] 陈艳秋，郭宝亭，朱梓根.金属橡胶减振垫刚度特性及本构关系研究[J].航空动力学报,2002,17(4):416-420. Chen Yanqiu,Guo Baoting,Zhu Zigeng. The Research of Metal Rubber Damper Stiffness Characteristics and Equations[J]. Journal of Air Power,2002,17(4):416-420.

[7] 彭威，白鸿柏，郑坚，等.金属橡胶材料基于微弹簧组合变形的细观本构模型[J].实验力学,2005,20(3):455-462. Peng Wei, Bai Hongbo, Zheng Jian, et al. A Micromechanics Constitutive Model of the Metal Rubber Materials Based on the Radial and Axial Combined Deformation of the Microsprings[J].Experimental Mechanics,2005,20(3):455-462.

[8] 姜洪源，夏宇宏，敖宏瑞,等.金属橡胶与弹簧组合型隔振器动静态性能的分析[J].中国机械工程,2002,13(21):1801-1804. Jiang Hongyuan , Xia Yuhong ,Ao Hongrui， et al. Metal Rubber and Spring Vibration Isolation Device Combination of Dynamic and Static Performance Analysis [J]. China Mechanical Engineering, 2002, 13 (21) : 1801-1804.

[9] 姜洪源，夏宇宏，敖宏瑞.金属橡胶构件的性能分析与实验研究[J].中国机械工程,2001,12(11):1294-1297. Jiang Hongyuan, Xia Yuhong, Ao Hongrui. The Performance Analysis and Experimental Research of Metal Rubber Components [J]. China Mechanical Engineering, 2001, 12 (11) : 1294-1297.

[10] 刘辉航，张英会.弹簧手册[M].北京：机械工业出版社，2008.

[11] 李冬伟，白鸿柏，杨建春,等.金属橡胶弹性元件实验建模研究[J].兵器材料科学与工程, 2005,28(3):7-10. Li Dongwei, Bai Hongbo, Yang Jianchun, et al. The Experiment Study of Metal Rubber Elastic Element Model[J]. Journal of Weapon Materials Science and Engineering, 2005,28(3):7-10.

[12] 刘家燕，程志峰，王平.机载光电吊舱橡胶减振器的设计与应用[J].中国机械工程,2014,25(10):1308-1312. Liu Jiayan, Cheng Zhifeng, Wang Ping. The Design and Application of Airborne Electro-optical Pod Rubber Shock Absorber [J]. China Mechanical Engineering, 2014,25 (10) : 1308-1312.

[13] 李宇明，彭威，白鸿柏，等.金属橡胶材料宏观和细观力学模型[J].机械工程学报,2005,41(9):38-41. Li Yuming, Peng Wei, Bai Hongbo, et al. Mechanical Model of Metal Rubber Material in Macro and Micro Level[J]. Journal of Mechanical Engineering,2005,41(9):38-41.

(编辑 王旻玥)

Research on Stiffness Characteristics and Mechanics Model of Metal Rubbers

Yu Huijie Liu Wenhui Wang Yasu

University of Shanghai for Science and Technology, Shanghai, 200093

The mechanism of metal rubber molding and the influence factors of static stiffness characteristics were analyzed, on the basis of the theory of helical spring stiffness metal rubber an infinitesimal spring theoretic model was established. According to the test results, the model was corrected. Through the comparison of theoretical model and experiments, the results show that the theoretical values are close to the experimental ones, which may comprehensively reflect the static stiffness characteristics of metal rubbers and provide the theoretic basis for the design of the metal rubber dampers and the determination of metal wire processing parameters.

metal rubber; static stiffness characteristics; mechanics model; processing parameter

2016-05-24

上海市军民融合专项项目(201643)；上海市青年科技英才扬帆计划资助项目(16YF1408000)；上海市自然科学基金资助项目(16ZR1423600)

TB302

10.3969/j.issn.1004-132X.2016.23.008

余慧杰，男，1978年生。上海理工大学机械工程学院讲师、博士。主要研究方向为电子设备结构优化设计、隔振系统设计及人机工程动态仿真。发表论文10篇。刘文慧，女，1989年生。上海理工大学机械工程学院硕士研究生。王亚苏，男，1989年生。上海理工大学机械工程学院硕士研究生。