几何计算题的基本方法和策略
山东省单县希望中学(274300)秦令忠
几何计算题的基本方法和策略
山东省单县希望中学(274300)秦令忠
近年来,在以圆为背景的图形中求线段长,是各地中考的高频考题,是圆与相似、解直、方程的联系题目,学生对于此类问题中的第二问的解决上还存在困难.我在多年的教学中重点这样指导学生:学会寻找几何元素之间的联系,用综合分析法建立圆与相似、解直、方程的联系,从而应用求线段长的基本方法.下面我从几个例题中与同行们交流:
例1.已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,
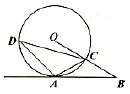
图1
(1)求证:AB是⊙O的切线;
(2)若∠ACD=45℃,OC=2,求弦CD的长.
【分析】(1)连半径证垂直是证明切线的一种常用方法,此题中根据所给线段的数量关系,可以直接证得∠OAB=90℃;(2)由于已知45℃,学生很容易联想到过点A作垂线这条辅助线,在△ACE中可求出CE和AE,DE可在△ADE中求得,为了使△ADE可解,还需要一个条件,因此,此题的关键是从∠O=60℃转化到∠D=30℃,运用解直求线段长.

图2
解:(1)证明:如图,连结OA

∴AB是⊙O的切线.
(2)解:作AE⊥CD于E点.
∵OC=OA=OC
∴△ACO是等边三角形
∴∠O=60℃∴∠D=30℃
又∠ACD=45℃,AC=OC=2,
在Rt△ACE中,∵∠D=30℃,

【设计意图】
1.体会圆是转化角的一个工具,此题中将等边三角形提供的圆心角与圆周角联系起来,易知∠D=30℃.
2.巩固上节课的解三角形求线段长的思路
3.圆与解直的联系,此题中在解△ACD时,可以用化斜为直的方法.
例2.已知:如图,在△ABC中,AB=AC,AE是角平分线, BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于点G,交AB于点F,FB恰为⊙O的直径.

图3
(1)求证:AE与⊙O相切;
【分析】(1)题应用等腰三角形三线合一易证出∠AEB=90℃,为了证∠AMO=90℃,只需要证明OM//BC,由角平分线和等腰三角形转化角易得(2)题中经过推理将条件集中在Rt△AEB中,由于已知BE和cos∠CBA的值,因此,Rt△AEB可解,将所求的半径放入Rt△AMO中,用设参法表示出Rt△AMO的边长,然后通过这两个三角形相似构造比例式方程解决;或通过转化角,将Rt△AEB中的条件转化到Rt△AMO中,运用锐角三角函数的知识解决.
解:(1)证明:连结OM,则OM=OB.


图4
在△ABC中,AB=AC,AE是角平分线,
∴AE⊥BC.∠AEB=90℃.
∴∠AMO=90℃.∴OM⊥AE.∴AE与⊙O相切.
(2)解:在△ABC中,AB=AC,AE是角平分线,


【设计意图】
1.圆与相似的联系,此题中通过已知条件找到可解的三角形,将未知线段所在的三角形与可解的三角形建立联系,通过相似求线段长是一种常见方法,此题中两个相似的三角形是直角三角形,因此也可以用三角法解决.
2.设参法的应用,体会方程的工具性.
例3.已知:如图,AB是⊙O的直径,C是⊙O上的一点,且∠BCE=∠CAB,CE交AB的延长线于点E,AD⊥AB,交EC的延长线于点D.

图5
(1)判断直线DE与⊙O的位置关系,并证明你的结论;
(2)若CE=3,BE=2,求CD的长.
【答案】
此题(1)可通过已知条件∠BCE=∠CAB和图形条件(圆中等腰——半径转化角)将∠OCE与直径所对的圆周角∠ACB建立联系,从而证明∠OCE=90℃.(2)中CD=AD,找到含有它们的三角形,且能与其它三角形建立联系求解,因此,找到△ADE与△COE相似,求出半径就解出了△COE,从而能解得

【设计意图】
1.圆与方程的联系,此题中用勾股定理建立方程求解圆的半径,用相似或三角法建立方程求出未知线段长.
2.一题多解,变式训练,提高思维的灵活性,学会优化选择.
3.用问题串引导学生深入思考.
问题串:(1)为了证明切线,根据已知条件,可证哪个角为直角,这个思路是否可行,为什么?
(2)含未知线段的三角形不可解?怎样与其它三角形建立联系?
(3)与它相似的三角形是否可解,为什么?
(4)还可以用什么方法求半径长?
(5)如果不先求出半径长,能否解决此题?
(6)哪种方法更优化,为什么?
此题求半径的方法多样,可在Rt△OCE中通过勾股定理建立方程求半径,也可通过公边共角图△ACE与△CBE相似求半径,还可建立Rt△OCE与Rt△DAE之间的相似关系,通过方程组同时求半径和未知线段长,大家不妨一试.另外,此题中求出半径长之后,结合切线长定理可以在Rt△DAE中应用勾股定理求解,但相比而言,所列方程是二次方程,就不如一次方程简单.
例4.如图,AB、CD是⊙O的两条弦,它们相交于点P,联结AD、BD.已知AD=BD=4,PC=6,求CD的长.

图6
【答案】通过连结AC可将所求线段CD置于△ACD中,这个三角形不可解,因此,可以找相似三角形,虽然△APC~△DPB,但求不出PD,因此,需要找别的相似三角形,通过标记圆中的等角,易发现△DPA~△DAC,从而求出CD=8.
【设计意图】当找不到可解的三角形时,可以建立两个三角形之间的联系,应用相似求线段长.此题中有公边共角的圆中相似,在公边共角这个基本图形的相似中,通过夹公共角两边的边长的对应关系列出方程求线段长.
(三)练习

图7

图8
1.如图7,在△ABC中,∠C=90℃,AD是∠BAC的平分线,O是AB上一点,以OA为半径的⊙O经过点D.
(1)求证:BC是⊙O切线;
(2)若BD=5,DC=3,求AC的长.
2.如图8,已知AB为⊙O的弦,C为⊙O上一点,∠C=∠BAD,且BD⊥AB于B.
(1)求证:AD是⊙O的切线;
(2)若⊙O的半径为3,AB=4,求AD的长.
3.已知:如图9,在Rt△ABC中,∠ABC=90℃,D为AB上一点,以BD为直径作半圆O,与AC相切于点E,若BD=BC=6,求AC的长.

图9

图10
4.如图10,AB、BC、CD分别与⊙O切于E、F、G,且AB//CD.连接OB、OC,延长CO交⊙O于点M,过点M作MN//OB交CD于N.
(1)求证:MN是⊙O的切线;
(2)当0B=6cm,OC=8cm时,求⊙O的半径及MN的长.
5.如图11,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线的一点,AE⊥CD交DC的延长线于E,CF⊥AB于F,且CE=CF.

图11
(1)求证:DE是⊙O的切线;
(2)若AB=6,BD=3,求AE和BC的长.
6.问题背景:在某次活动课中,甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:
甲组:如图12,测得一根直立于平地,长为80cm的竹竿的影长为60cm.
乙组:如图13,测得学校旗杆的影长为900cm.
丙组:如图14,测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细忽略不计)的高度为200cm,影长为156cm.

图12

图13
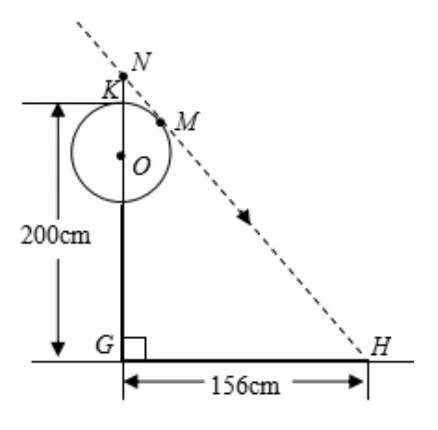
图14
任务要求
(1)请根据甲、乙两组得到的信息计算出学校旗杆的高度;
(2)如图14,设太阳光线NH与⊙O相切于点M.请根据甲、丙两组得到的信息,求景灯灯罩的半径(友情提示:如图3,景灯的影长等于线段NG的影长;需要时可采用等式1562+2082=2602).

