百花齐放,各显其艳—如何在课堂中训练学生的思维

福建莆田四中数学组(351100)黄雄林

百花齐放,各显其艳—如何在课堂中训练学生的思维

福建莆田四中数学组(351100)黄雄林

提高学生的数学思维能力,是数学教育的基本目标之一,如何打破传统课堂教学陈规,在数学课堂上发挥学生学习的主动性,在教师的组织下通过学生的自主探究,将课堂中的思维空间让给学生,是当前数学课堂变革的新特点.下面通过我的一节思维活动课来谈谈如何在课堂上训练学生的思维.

(一)立足基础、全员参与

课堂教学是面对班级全体学生的教学,而不是部分学生、个别同学的教学,因此要让每个学生都有参与思维的机会,激发每一个学生的思维是我们教学的前提.这就要求我们在备课时就应立足基础,面向全体学生.本节课我以教材的一道课后习题为引例,展开了学生的思维训练.

例1.写出过点A(−5,3),并且和曲线xy=1相切的两条直线方程.(湘教《数学》选修2-2 P17)

我先让学生思考片刻,并通过分组讨论、合作交流,然后各组选派1名同学上来板演.发现了两种不同的求解方法:

【方法1】解:由数形结合知过A(−5,3)的曲线xy=1的切线斜率存在,设切线斜率为k,方程为y−3=k(x+5).由

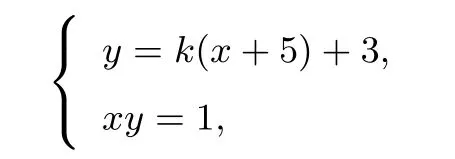
消去4y得:x[k(x+5)+3]−1=0,整理得

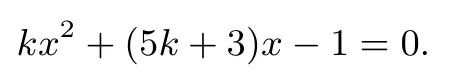
因为直线与曲线相切,故

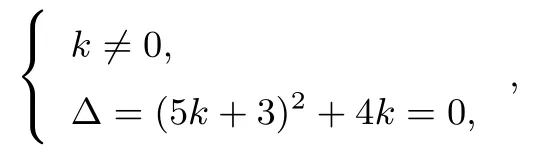
整理得

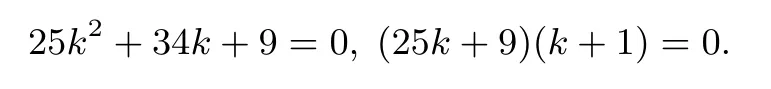
学生们从不同的思维角度解决了求过某点的曲线的切线方程.有效地防止了思维定势的发生.方法1使用直线与二次曲线关系中求曲线的切线的“∆”法;方法2利用了函数的导数的几何意义,通过求导的办法来解决问题.这两种方法都是高中数学的基本方法,涉及到的都是基础知识,学生易于接受且都能应用.同时也让大家都能感觉到动手实践,合作交流的乐趣,同学们体验到了成功的喜悦.

(二)趁胜追击,继续前进

趁着大家在感受成功喜悦,我展开了本节课的创造性思维活动,来引领大家发现、提出问题展开思维空间.于是,我开始提出问题:“上例求出的两条切线方程和 y=−x−2,它们与两坐标轴围成的面积分别是多少?”通过一分钟多的运算、求解,大家得到了相同的结论:两切线与坐标轴围成的面积均为2平方单位.

“是不是过曲线xy=1上每个点的的切线与坐标轴围成的面积都是2平方单位?”带着疑问的表情,和着同学们的好奇心,激起了大家的探究热情.

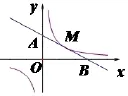
图1

得到了统一的结果:曲线xy=1上任一点处的切线与两坐标轴围成的面积均为定值2平方单位.原来数学中蕴藏着这么多的奥秘,同学们真是兴奋不已.同时,这节课同学们的思维也已进入了高潮,我感觉火候已到,开始了本节课的探究活动.

(三)抓住时机,适当探究

(方法1)设出曲线的切线方程,利用“∆”法求出切线的方程,并证明它与两渐近性围成的面积为定值1平方单位.

(方法2)根据图形的对称性,设(x0,y0)为曲线上第一象限内的点,把双曲线x2−y2=1化为函数利用函数的导数的几何意义,通过求导的方法得到切线方程来解决,也得到了相同的结论.

但这一次我又发现了一个意外,有几个同学正在激烈的讨论着另一种方法,他们是应用圆锥形曲线上某点处的切线系方程来证明,其方法过程如下:

(方法3)图2,设过曲线x2−y2=1右支上的点M(x0,y0)的切线方程为x0x−y0y=1,与双曲线的两渐近性方程为y=x和y=−x相交于A、B两点,在切线x0x−y0y=1中:令y=0得得直线xx−yy=1与x00轴交点令y=x得x0x−y0x=1,x

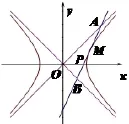
图2

为定值.当点(x0,y0)为双曲线左支上的点时同理可证得.

原来他们使用了圆锥曲线上某点处的切线系方程的结论:过双曲线上的点(x0,y0)的切线方程为简洁的思维方法,简练的解题过程令同学们观为叹止,兴奋不已.我也得到了意外的收获.

为了把思维延伸到课外,我给他们布置了两道探究性思考题:

1.已知顶点为原点O,焦点在x轴上的抛物线y2=16x,过抛物线上一动点M作抛物线切线l,又MN⊥l且交抛物线于另一点N,ME(E在M的右侧)平行于x轴,若∠FMN=λ∠NME,求λ的值.(答案:λ=1.思维目标:旨在引导学生理解运用曲线的点A(x0,y0))处的切线方程为:以及曲线y2=2px上,点 B(x0,y0)处的切线方程为:y0y=p(x0+x)).

这一节课引用了在曲线上某点处的切线方程的求法,以及曲线上动点处的切线与两定直线围成三角形面积的定值问题等知识点,通过了合作讨论,自主探究等教学方法,全面有效地训练了同学们的思维,也让所有的同学都能在这一节课中得到收获.同时我依据学生已有的知识背景和活动经验,提供学生更多的操作、思考和交流的机会,使学生通过自己探索与合作交流形成了新的知识.课堂上充分利用创设“问题”的教学方法,结合教学内容,提出问题,拓展学生的思维空间,发挥学生“自主学习,合作探究”的学习主动性.通过师生互动,面向全体,引发学生的学习兴趣,激发了学生的求知欲,使学生在愉快和谐的交流中满怀激情地学习.