融合知识与技能提升学力与智力—谈切实提升学生数学解题能力的策略研究
江苏省海门市海南中学(226100)江斌杰
融合知识与技能提升学力与智力—谈切实提升学生数学解题能力的策略研究
江苏省海门市海南中学(226100)江斌杰
评价数学知识学习效果的一个重要标准就是学生们能否运用所学方法来准确解答数学问题.很多学生在初中数学学习过程当中,自认为已经将知识内容掌握到位了,可在面对具体数学问题时,却总是会出现这些那些的错误,甚至是无从下手,困难重重.这也体现出了数学学习当中的一个重大误区:只顾单一的理论知识学习和积累,却忽略了将知识方法向应用方向的转化,将知识与技能巧妙的融为一体.这将导致数学知识学习浮于表面,无法切实达到预期教学效果.为此,帮助学生将理论知识与学生所学的知识巧妙的融合为一体,打通学习与应用之间的通道,将学生们的数学解题能力提升起来,便成为了当前初中数学教师们的首要任务.
一、善于运用图形,提升数形结合能力
在初中数学当中,看似晦涩的理论性语言往往都是可以通过图形来将之巧妙描绘出来的,这也体现出了“数”与“形”之间的等价转化关系.这种思路运用到题目解答当中也是非常适合的.面对很多比较复杂的数学问题时,如果能够另辟蹊径,从图形的角度来切入思考,往往能够获得意想不到的思路启发.这也是初中数学当中经常会运用到的重要方法——数形结合.
例如,在对函数内容进行教学时,我特意选择了这样一个问题请学生们试着解答:现有两个函数y=kx+k和若将二者的图象表示在同一个平面直角坐标系当中,应当是如下哪种情况?(如下图)这个问题的解答关键有二:一是对一次函数和反比例函数概念与特点的把握,二是以图象的方式对函数的走势进行表示的能力.为此,学生们不仅需要分析函数本身,还需要对图象进行识别.经过一系列分析,大家在得到了C的正确答案之后,还切身体验到了图形对于数学问题解答的重要性.在今后的函数问题分析过程中,即使题目没有给出图形,学生们也会建立起自己画图,配合思考的意识.

图1
数形结合这一思想方法对于初中数学问题解答来讲至关重要.仔细观察便不难发现,在数学语言的表面覆盖之下,是一幅具体、动态的画面.这幅画面往往会成为顺利解题的关键,而想要顺利构造出这幅画面,就需要将数字与图形巧妙结合起来,以数字描述图形,以图形阐释数字.通过生动的图形,实现了对理论知识的有效具化,进行解题自然顺畅了许多.而在常态的教学过程中,教师要创设机会和氛围让学生通过深入的观察、分析、对比、应用来达成数形结合思想的领悟、应用、内化.
二、巧引自主总结,提升逻辑思维能力
数学知识内容的呈现方式五花八门,由其所出现的相应习题更是多种多样.面对这样的数学题目现状,想要站在一个更高的角度以统筹的眼光来进行分类、总结、归纳.这就需要从中总结出一些规律性的方法,从而提纲挈领地把握题目解答.这样一来,一方面,学生们的解题思路能够瞬间清晰起来,另一方面,也能够为学生们缓解许多学习与思考的压力,有效的服务于学生解题能力的提升,服务于自主学习能力的提升,真正达成减负高效的理想效果.
在解题方法的引导之下,原本杂乱无章的数学问题一下子变得条理清晰起来了.总结出的这些方法就像一条条线,将零散的知识内容快速串连起来.学生们作为这些线的主人,只要牵起线的一个端点,便可以将整串知识点拎起来,以之解答出一整类的数学问题.与此同时,教师们还要注意,总结解题方法并不是教师一人的工作,而应当是由教师引导学生自主得出,这是有效提升学生逻辑思维能力的绝佳时机.
三、变通生活实际,提升知识应用能力
在初中数学的各类测验当中不难发现,几乎每一次都会或多或少地出现应用题的身影.这种高频率的考查状态,不仅反映出了应用题在初中数学学习当中所占据的比重,更揭示出了知识应用能力对于当前教学的重要性.如果说,将理论知识运用于问题解答,是对知识的一种应用转化,那么,将知识继续具化,投入到对实际生活当中的问题的解答当中去,便是对理论知识的二度深入应用了,而且,将数学知识与技能变通的服务于生活实际,可以充分彰显数学的学科魅力,更能提升学生的实际应用能力.因此,变通生活实际,提升学生的实践应用能力,是学科的需要、学生的需要,更是社会发展的需要,这一需要对数学的教与学提出了更高要求.
例如,在学习过立方体的知识后,我请学生们思考这样一个问题:现有一个长方体的铁块,其长、宽、高分别为15厘米、12厘米、8厘米.现将这个铁块熔化,重新锻造成为一个底面边长为12厘米的长方体铁块.那么,前后两个铁块相比,哪一个的表面积更大?经过分析,学生们透过“熔化”一词发现了问题当中的等体积关系,并结合立方体表面积与体积的计算方法,很顺利地将问题解答出来了.学生们高涨的思考热情,与问题当中的实际生活痕迹不无关系.随着问题的解答,大家收获了解决生活问题的成就感,并随着应用能力的提升,深化了知识理解.
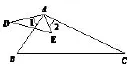
图2
运用所学数学知识解决实际生活当中的问题,并不是为学生们的学习活动增加负担,而是为有效学习提供了一条有效深化的捷径.当学生们真正能够做到联系实际,学以致用时,证明大家对相应知识内容已经形成了比较准确的理解.而当学生们成功运用所学知识解决自己身边的实际问题之后,学习热情也会随之显著提升,这种自信也会继续反作用于接下来数学知识的继续探究.
四、适时拓展延伸,提升创新学习能力
数学问题的灵活性一直是让很多学生感到头疼的地方.如果问题只是将需要考查的知识内容直接呈现出来,学生们的思考方向会很明确,问题解答起来也不会过于困难.但是,当这些知识方法间接地隐藏在灵活多变的题目形式之下时,便会给学生们造成不小分析和处理上的障碍.大家需要抽丝剥茧地从问题表面分析出真正的知识考查之处,再选择正确的思路方法予以解答.这就需要学生们在夯实知识基础的前提下,明确问题形式变化的规律与路径,更好地从看似复杂的问题当中发现数学.
例如,在带领学生们学习过相似三角形的内容之后,我发现,教材上为学生们设计的思维方向都是正向的,即已知两个三角形相似,得出相应的边角关系.那么,为什么不能反其道而行之呢?于是,我将思维方向逆转,向学生们给出了下面的图形,并提出∠1=∠2的已知条件,由此提出问题:想要使得△ADE与△ACB相似,还应当添加一个什么条件?看似简单的问题变化,却完全改变了学生们固有的思考路径.在这样的逆向思维过程当中,学生们实现了变化之中的创新,相似三角形的知识也被大家掌握得更加灵活了.对于数学问题解答,作为教师来讲,与其让学生们遇到灵活问题时再临时进行判断分析,不如在知识教学过程当中便尽可能多地将知识内容以变换的方式展现出来,让这个判断分析的过程反客为主,让学生带着变通的目光来学习、积累、应用所学的知识与技能,让学生学会分析、学会变通,用不变的思想和方法来解决千变万化的题目和问题.这样一来,学生们在知识学习环节,头脑就是灵活的,且能够对知识内容的变化模式产生一个了解和预判.有了这样的心理准备之后,再让学生们去面对形式多样的数学问题,难度自然就会降低许多.这不仅可以大大减少学生们在数学问题解答时的精力投入,更可以提升大家的学习自信心.
只有能够运用所学理论知识将数学问题准确解答出来,学生们才算是在数学学习当中迈出了成功的一大步.想要实现从学习到运用的转化,并不是一件简单的事情.它需要建立在学生们对于理论知识的深入理解与准确把握的基础之上.也就是说,学生不仅要知道本次学习的知识内容是什么,更要知道怎么用其解答问题.在这个过程中,教师们需要尤为重视学生思维逻辑与思想方法的培养,运用巧妙方式对其进行引导与启发,让学生们得以在初中这个基础奠定阶段初步形成学以致用的意识与能力,为今后的数学问题解答与相关能力提升加注动力.

