远中心柔顺机构弹性单元刚度建模研究

常晏宁,王卓识,王 皓

(1.上海交通大学 上海市复杂薄板数字化制造重点实验室,上海 200240; 2.上海交通大学 机械系统与振动国家重点实验室,上海 200240)



远中心柔顺机构弹性单元刚度建模研究

常晏宁1,王卓识1,王 皓1、2

(1.上海交通大学 上海市复杂薄板数字化制造重点实验室,上海 200240; 2.上海交通大学 机械系统与振动国家重点实验室,上海 200240)

为得到远中心柔顺机构(RCC)中常用的金属梁单元、层叠弹性单元(ESP)的刚度性能，在材料力学四个基本假设下，根据弹性变形原理，对单元末端建立金属梁刚度矩阵，并通过伴随变换进行解耦，得到其对角形式。对端部具铰链梁单元、U副梁单元、球关节梁等不同运动副的单元进行刚度建模，给出铰链处的刚度矩阵，发现转动副处的刚度矩阵无法解耦，而U副和球副可解耦。建立了ESP弹性单元的刚度模型，发现在一端固定条件下，末端自由、添加U副和添加球副均利于形成RCC机构的解耦刚度性能。研究为RCC机构的设计提供了参考。

远中心柔顺机构； 刚度性能； 梁单元； ESP单元； 运动关节； 刚度矩阵； 伴随变换； 解耦

0 引言

RCC广泛用于自动化装配领域，远中心柔顺手腕使机器人具备一定的柔顺能力，可完成间隙为微米级的插销入孔装配作业[1-2]。柔性杆或具有铰链等结构的柔性杆是RCC装置常用的变形结构，用于提供可观的被动顺应性能以保证轴孔插入装配有效进行。在插轴入孔装配操作任务中，柔顺中心位置的设置十分重要，因此需对RCC机构中的弹性单元刚度进行分析[3]。RCC装置常用的弹性单元主要有金属梁单元、带多种铰链的金属梁单元，以及具橡胶金属片层叠结构的ESP单元。1986年，WHITNEY 首先介绍了用ESP单元设计RCC机构的方法，克服了传统RCC机构在采用线性弹簧模型预测时，刚度和柔顺中心误差较大的问题[4]。此后，采用ESP弹性单元的孔轴装配被动顺应柔性手腕被广泛应用。为提高装配的灵活性和可靠性，提出了可变远中心柔顺机构(VRCC)的设计方案，其特点是柔顺中心的位置可根据工作需要改变[5]。但弹性单元不利于通过变动VRCC装置结构尺寸改变刚度性能，只能通过改变弹性单元长度或弹性部位实现可变的刚度性能，这种结构过于复杂且不利于悬挂较重零部件时的调节。一端具有转动副、U副等运动副形式的弹性单元因其转动副的适应能力，便于实现RCC装置改变尺寸进而改变刚度性能，因此本文建立具有铰链的金属梁及ESP刚度模型。目前，针对RCC机构的研究主要是整体方案的设计及分析，未对构成RCC机构的弹性单元在不同铰链下的刚度性能进行系统的分析和比较。关于弹性单元刚度性能的研究，文献[6]给出了弹性梁的刚度矩阵算法，文献[7]给出了变截面梁的刚度矩阵求法，但并未对刚度矩阵尝试进行解耦。另对ESP单元刚度矩阵的建立及解耦方法则尚未有针对性研究。在材料力学的连续性、均匀性、各向同性、小变形四个基本假设前提下，本文对金属杆和ESP等弹性单元末端的刚度性能矩阵建立进行了研究，并用伴随变换将刚度矩阵转为解耦形式的对角化刚度矩阵，判断该单元的解耦性能，以此比较梁单元和ESP单元在不同运动关节连接时的刚度性能，为RCC设计中弹性元件的选取及刚度参数的优化提供参考。

1 金属梁刚度模型

金属梁单元如图1所示。柔性单元末端点O变形可表示为Δx=[uTγT]T。此处：u为末端三个方向的微小位移变形；γ为末端绕三轴的微小转动变形。末端点O受力可表示为F=[fTτT]T。此处：f为末端受力；τ为末端所受弯矩。在满足线性假设时，柔性单元的刚度可表示为

F=KOΔX.

(1)

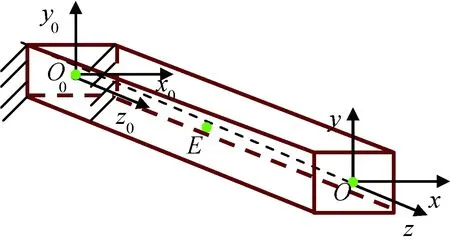
图1 金属梁单元Fig.1 Metal beam element

RCC装置梁单元的末端刚度性质不同于悬臂梁和固定梁，在工作过程中受定平台和动平台的约束，其刚度性能与有限单元方法中的梁单元相似。在满足材料力学四个基本假设的前提下，等截面金属梁单元的末端点O在O-xyz坐标系中的刚度性能可描述为

(2)

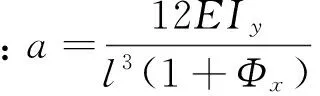
点E为等金属梁轴线中点，其在O-xyz坐标系中矢量可表示为OE=[0 0 -l/2]T。由文献[9]，将KO转为至点E的伴随变换矩阵可表示为

(3)

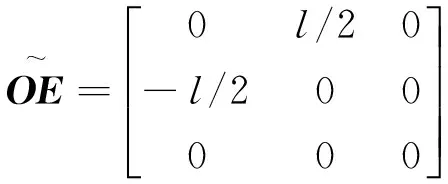
(4)

KO，KE间的转换关系可表示为

KE=(AEO)TKOAEO.

(5)

经变换，梁单元在位置点E的刚度矩阵可表示为

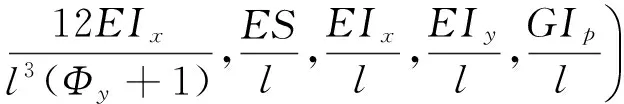
(6)

由式(6)可知：在该点梁单元的刚度矩阵具对角矩阵形式，各方向刚度解耦。弹性单元具有该形式的刚度矩阵，利于形成远中心顺应机构的末端解耦刚度性能。

2 运动副梁单元刚度模型

2.1 铰链梁单元刚度模型

如图2所示为一端固定，另一端铰链连接的金属梁单元。O-xyz坐标系与铰链固定端固结，点O位于梁中心点，Ox轴与铰链旋转轴重合。惯性坐标系O0-x0y0z0位于梁单元中心点，建立末端点O的刚度模型。理想条件下，铰链未改变ux，uz，γy，γz向的约束，以上四个方向具有与普通等截面梁单元相同的刚度性能，只需对uy，γx向进行刚度建模。

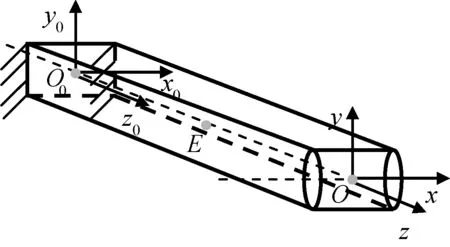
图2 铰链金属梁单元Fig.2 Hinged metal beam element

先对uy向进行刚度建模。在横向力fy和扭转力矩τx的作用下，末端点O的uy变形可表示为

uy=ub+us.

(7)

式中：ub为由力矩τx引起的位移；us为由剪切力fy引起的位移。两者线性叠加构成该点的变形位移。us，ub的变形特征可表示为

(8)

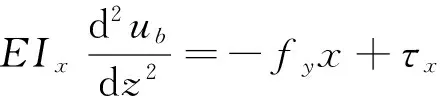
(9)

由于末端点O铰链不受扭转力矩，故τx=0，即理论上铰链光滑不受力。将以上关系联立代入式(7)可得

(10)

固定端点O0不会发生形变，同时铰链梁单元末端不受弯矩作用，其受力产生的弯曲在固定端将完全取决于铰链端的剪切力。归纳以下两个变形约束条件：

b)x=-l时，uy=0。

将两约束条件代入式(10)，可算得式中常数项为

(11)

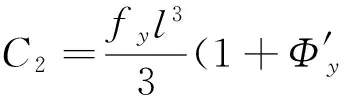
(12)

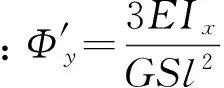
O-xyz坐标系中梁末端点O处x=0，则该点在y向变形

(13)

以上表示y向的柔度性能，转为刚度方程形式可得

(14)

分别对fy，τx求uy的导数，可得

(15)

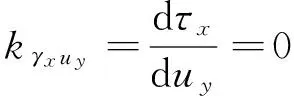
(16)

τx对uy影响的形变量为零可理解为铰链固定端受τx的扭矩作用，但该扭矩并不能传递至铰接梁单元，因此其γx向不产生形变，柔度无穷大。顺应机构末端受到该方向的扭矩作用时，由于存在多个弹性单元，所受扭矩可转为多个大小相等方向相反的力或该扭矩作用于具该方向刚度的弹性元件上。

再对γx向进行刚度建模。因τx不会传导至梁单元，且梁末端受固结于RCC装置上，fy不会产生γx向变形，故γx向不会产生变形，其刚度矩阵中各项可表示为

(17)

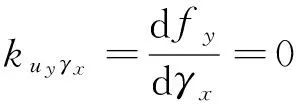
(18)

综上所述，铰链梁单元末端点O的刚度矩阵可表示为

(19)

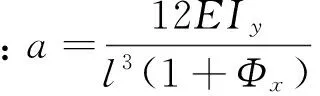
2.2 U副梁单元刚度模型

建立末端有U副的梁单元刚度模型，结构如图3所示。

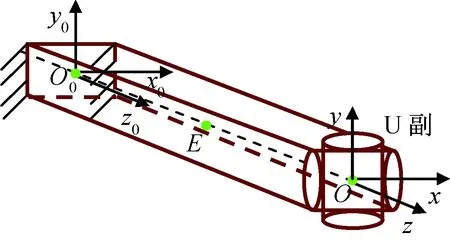
图3 U副金属梁单元Fig.3 Universal jointed metal beam element

末端有U副的金属梁单元相当于在末端具有两个轴线垂直相交，转动轴与梁轴线相交于一点的弹性单元，因此其刚度性能可按两个铰链机构建模。由式(19)可得U副梁单元的刚度模型为

(20)

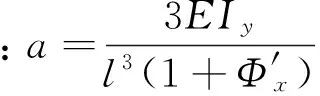
2.3 球关节梁单元刚度模型

建立球关节梁单元刚度模型，结构如图4所示。

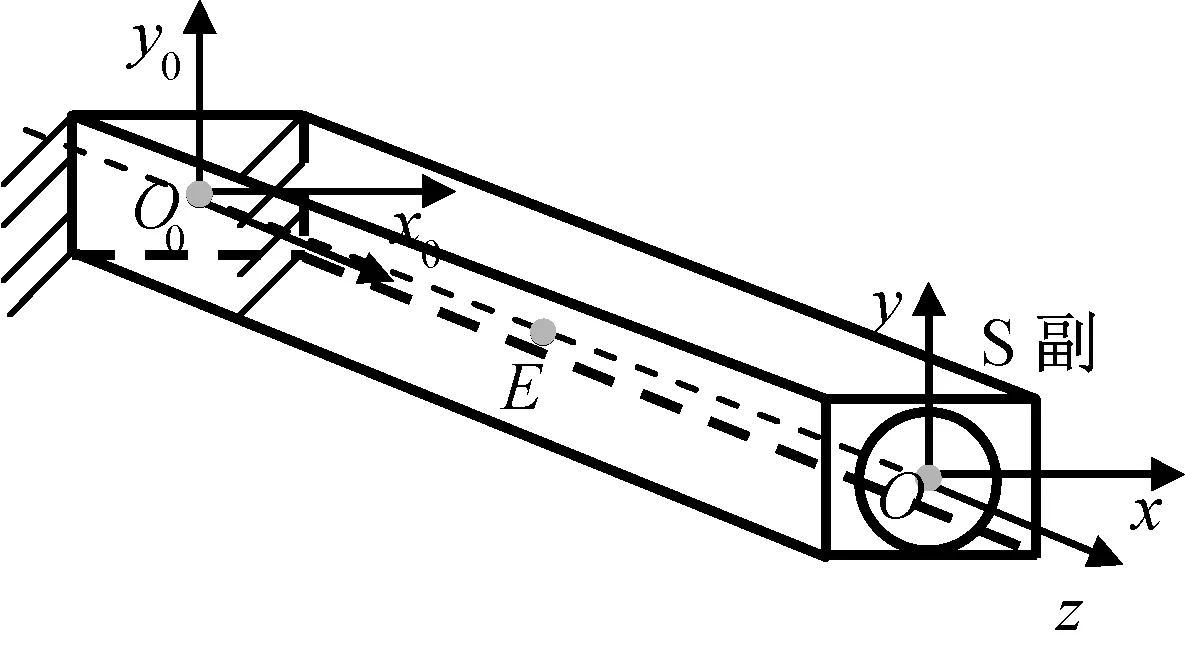
图4 球关节梁单元Fig.4 Ball-jointed metal beam element

对末端具有球铰链的梁单元，末端球铰链处不承受扭转力矩，ux，uy，γx，γy向刚度性能与2.2节中U副梁单元相同。uz向刚度不受球铰链存在的影响，γz向的扭转刚度为零，因此球铰链梁的刚度性能表示为

(21)

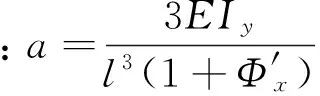
3 ESP弹性单元刚度模型

ESP单元的结构如图5所示。其中每个橡胶片与金属片构成一个弹性层，是ESP弹性结构的基础单元。设弹性层长度为t，称为弹性层节距；δ为橡胶层厚度；r0为有效承载横截面的半径。ESP弹性单元有n层弹性层，每层可视作简单梁单元。因金属片刚度远大于橡胶材料，故模型中不考虑金属片的刚度，即假想金属片为刚体，进而可通过刚度叠加原理组合橡胶层刚度得到整个弹性杆末端的刚度性能[10]。橡胶材料的拉压刚度相差较大，需用等效弹性模量概念分析橡胶的纯弯曲变形[11]。

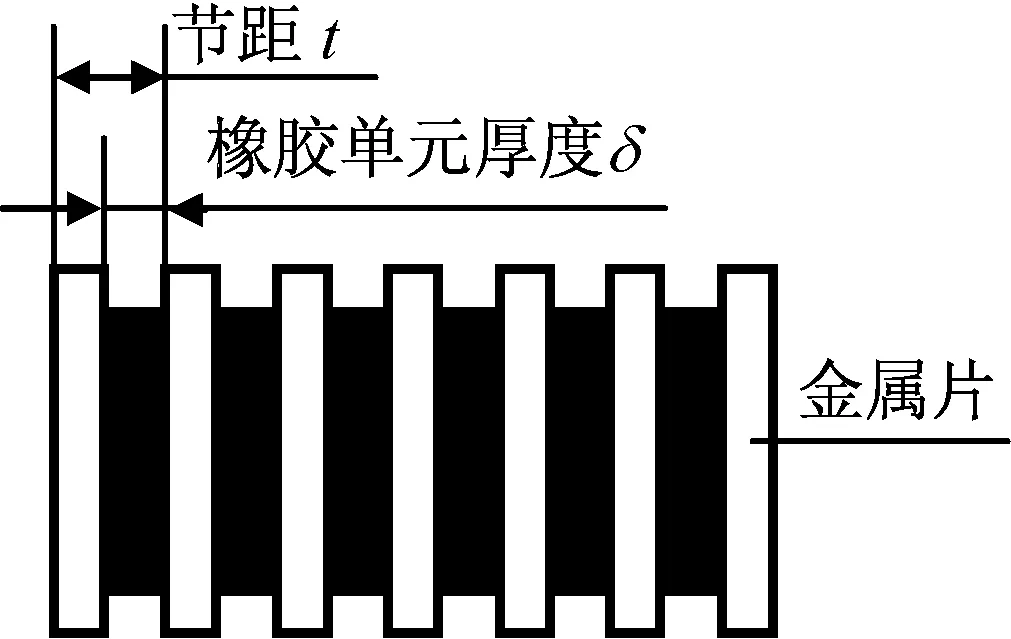
图5 ESP结构Fig.5 Structure diagram of ESP

由于方形截面的ESP单元具有金属粘结性不足，可能出现受力集中的问题，ESP单元采用圆形横截面结构，进行刚度分析，其结构如图6所示。图中：点O0为弹性单元固定端截面中心点，作为ESP单元起始点；点O为弹性单元末端中心点；点Oi为第i个弹性层末端横截面上中心点。

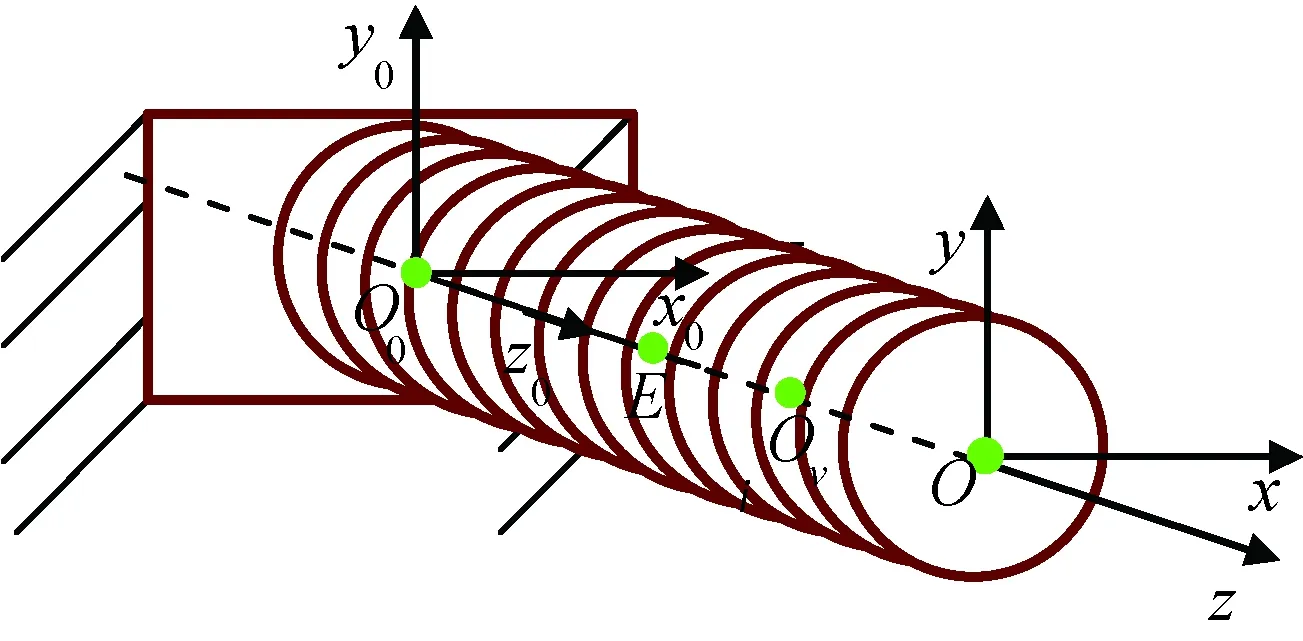
图6 ESP弹性单元Fig.6 ESP Element

各弹性层末端中心点Oi的刚度矩阵可表示为

(22)

点E为等截面梁轴线上一点，其位置距点O距离L=(n-1)t+δ/2。各弹性层末端点Oi相对点E的距离为li=-L/2+(i-1)t，在O-xyz坐标系中获得矢量OiE=[0 0li]T，将KOi转为至点E的伴随变换矩阵可表示为

(23)

式中：

(24)

KOi由伴随变换转换得到在点E处各弹性层的刚度性能并叠加。因各弹性层为串联连接，故需用柔度叠加的方法计算KE，有

(25)

转换后得点E位置的刚度矩阵为

KE=diag(K1,K2,K3,K4,K5,K6).

(26)

式中:

由此可知：在该点梁单元的刚度矩阵具对角矩阵形式，各方向刚度解耦。

4 U副ESP弹性单元刚度模型

同铰链金属弹性单元的刚度性质类似，有一个铰链的ESP弹性单元不具通过变换获得对角阵形式刚度矩阵的性质。因此建立末端为U副的ESP单元刚度模型，其结构如图7所示。

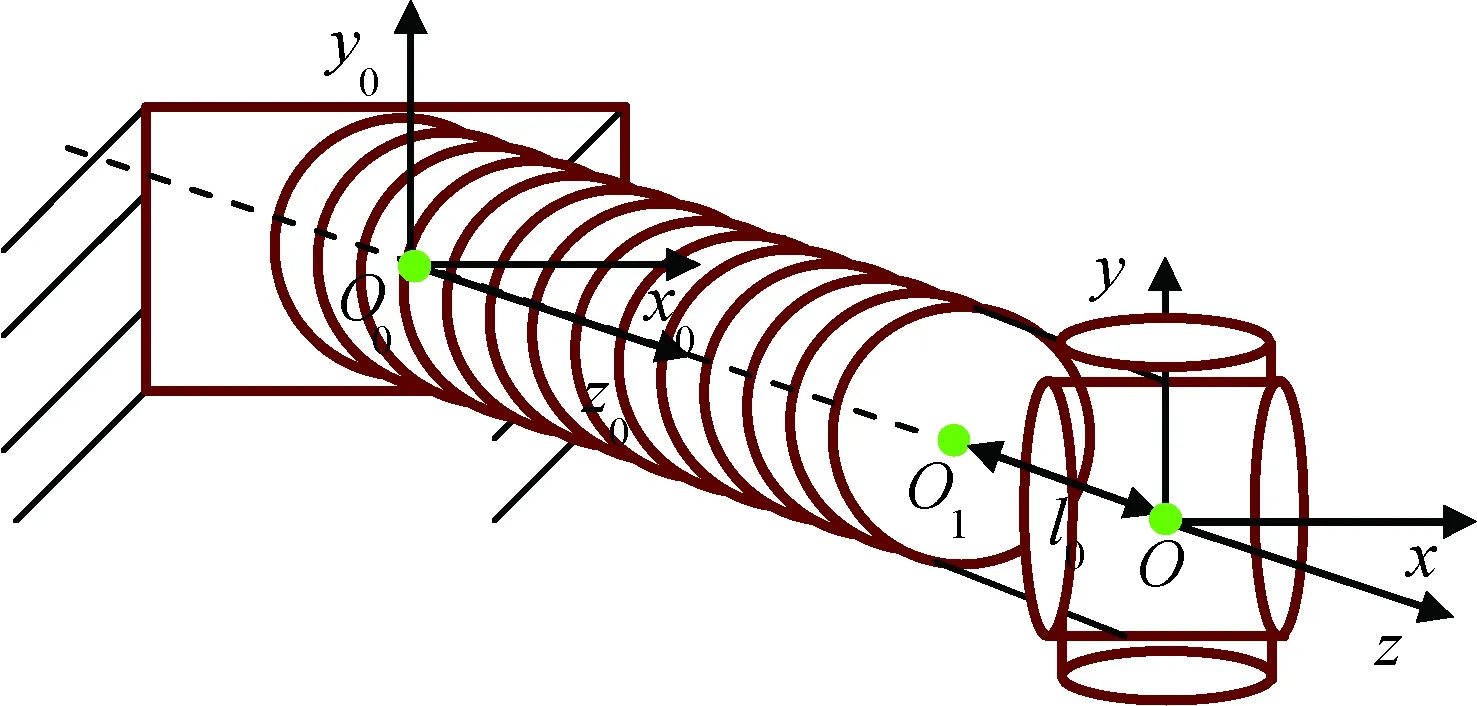
图7 U副ESP单元Fig.7 Universal-jointed ESP element

点O0至点O1为ESP弹性单元，点O1至点O为刚性连接杆，长度为l0。在U副弹性单元转动副一端沿x轴方向施加力Fx于点O，在点O1将产生力Fx和力矩Fxl0。点O1的ESP弹性元件受力可表示为

F=[fx0 0 0 τy0]T.

(27)

式中：fx=Fx；τy=Fx·l0。由外力同变形量关系式为

ΔXO1=(KO1)-1F.

(28)

可得点O1变形量为

ΔXO1=[ux0 0 0 γy0]T.

(29)

因点O的U副固定端不产生角度变化，则点O变形量可表示为

ΔXO=[ux+γyl00 0 0 0 0]T.

(30)

则点O的x向位移刚度可表示为

(31)

同理可得点O的y向位移刚度，由于U副不传递x、y轴向的扭矩，因此其刚度矩阵可表示为

KO=diag(KOx,KOy,KOz,0,0,Kτz).

(32)

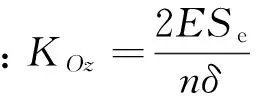
KO=diag(KOx,KOy,KOz,0,0,0).

(33)

5 结束语

本文根据材料力学原理建立了具有金属梁或ESP结构的不同弹性单元的刚度模型，并通过伴随变换进行解耦。同时，在弹性单元末端添加转动副、U副和球副，分析其刚度矩阵的解耦性，证明了在金属梁单元或ESP单元末端添加转动副(铰链)后，其刚度矩阵无法解耦，而U副和球副可解耦。通过对RCC机构中常用的两种弹性单元在不同铰链约束下的刚度性能进行比较，可为基于上述两种单元的RCC机构设计提供借鉴和参考。在后续研究中，可用上述单元设计简单的RCC机构，以检验本文刚度模型的实际应用效果。

[1] WHITNEY D E, NEVINS J L. What is the remote center compliance (RCC) and what can it do?[M]. Cambridge: Charles Stark Draper Laboratory, 1978.

[2] 王刚, 唐蓉城, 黄时聪, 等. 机器人远中心柔顺手腕的参数优化[J]. 天津大学学报, 1994, 27(2): 131-135.

[3] KOSUGE K, SHIMIZU M. Planar parts-mating using structured compliance[C]// Intelligent Robots and Systems, 2001 Proceedings, 2001 IEEE/RSJ International Conference on. [S. l.]: IEEE, 2001, 3: 1477-1482.

[4] WHITNEY D E, ROURKE J M. Mechanical behavior and design equations for elastomer shear pad remote center compliances[J]. Journal of Dynamic System Measurement & Control, 1986, 108(3): 223-232.

[5] ZHAO F, WU P S Y. VRCC: A variable remote center compliance device[J]. Mechatronics, 1998, 8(6): 657-672.

[6] 李仁锋, 程永生, 文贵印, 等. 弹性梁刚度矩阵算法及应用[J]. 传感器与微系统, 2003, 22(8): 62-64.

[7] 肖玲, 李银山. 变截面梁单元刚度矩阵及稳定分析[J]. 工程力学, 1998(A01): 406-410.

[8] PRZEMIENIECKI J S. Theory of Matrix structural analysis[M]. New York: Dover, 1985: 70-79.

[9] 张跃辉. 矩阵理论与应用[M]. 北京: 科学出版社, 2011.

[10] 杜松年, 彭商贤. RCC 手腕层叠弹性杆理论分析及性能实验[J]. 天津大学学报, 1994, 27(4): 385-390.

[11] 刘鸿文. 材料力学[M]. 第4版. 北京: 高等教育出版社, 2004: 138-175.

Research on Stiffness Modeling of Elastic Element in RCC

CHANG Yan-ning1, WANG Zhuo-shi1, WANG Hao1, 2

(1. Shanghai Key Laboratory of Digital Manufacture for Thin-Walled Structures, Shanghai Jiao Tong University, Shanghai 200240, China; 2. State Key Laboratory of Mechanical System and Vibration, Shanghai Jiao Tong University, Shanghai 200240, China)

To obtain the stiffness performance of the metal beam element and elastomer shear pad (ESP) element in common use in the remote center compliance (RCC), the stiffness matrices were built according to the principle of elastic deformation and four basic hypothesis in the theory of material mechanics. The stiffness matrices were built at the end of each element and decoupled through adjoint transformation and the block-diagonal form were finally obtained. The stiffness models of the elastic element with different joints at the end were also built and stiffness matrices for the location of joints were given. It is found that stiffness matrices of universal joint and spherical joint can be decoupled, while revolute joint can not. Therefore, when the two kinds of elastic elements are fixed at one end, the decoupling stiffness performance for RCC can be achieved with no joint, universal joint and spherical joint at the other end. The research offers a reference to the design of RCC.

Remote center compliance; Stiffness performance; Beam element; ESP element; Moving joint; Stiffness matrix; Adjoint transformation; Decoupling

1006-1630(2016)05-0057-06

2016-07-05；

2016-08-01

国家自然科学基金资助(11472172)；973计划(2014CB046600)

常晏宁(1992-)，男，硕士生，主要研究方向为机器人学。

TP273

A

10.19328/j.cnki.1006-1630.2016.05.009