伸展机构地面屈曲试验的重力影响及修正方法研究

刘 涛,韩 涵,唐国安,崔琦峰,咸奎成,彭志龙

(1.复旦大学 航空航天系,上海 200433; 2.上海宇航系统工程研究所,上海201109)



伸展机构地面屈曲试验的重力影响及修正方法研究

刘 涛1、2,韩 涵2,唐国安1,崔琦峰2,咸奎成2,彭志龙2

(1.复旦大学 航空航天系,上海 200433; 2.上海宇航系统工程研究所,上海201109)

针对重力造成的空间伸展机构在轨环境与地面试验环境的差异，根据伸展机构的边界条件将其简化为根部固支、端部自由的悬臂梁模型，梁受均布力，理论计算了均布力和集中载荷对梁屈曲的影响。建立了14，30 m两种伸展机构的有限元模型，对伸展机构施加重力载荷，计算了其静态非线性，将特征值法获取的伸展机构非线性屈曲模态引入弧长法求解伸展机构的屈曲承载能力。结果表明：当伸展机构达到一定高度后，须对地面试验结果进行修正；均布载荷可近似等效为在伸展机构的端部施加0.32倍的集中力载荷。分析结果对指导同类伸展机构的静力试验有一定的指导意义。

伸展机构； 重力； 屈曲； 弧长法； 均布载荷； 集中力载荷； 地面试验； 修正

0 引言

空间伸展机构是目前在轨应用较多的大面积柔性太阳翼支撑机构[1-6]。其中，盘绕式伸展机构先后用于美国E0S AM-1中分辨率成像光谱仪搭载平台和日本SFU自由飞行平台，AEC-Able公司研制的FASTMast伸展机构被用于国际空间站，在轨展开长度达32 m，可支撑太阳翼面积276 m2。我国在建的空间站也将采用柔性太阳翼技术。伸展机构因其展收可靠性高、重量轻和构造简单等特点在大型航天器中的应用前景十分广阔。空间伸展机构在轨工作时所受的轴压载荷主要源于电池阵面张紧力，伸展机构的头部与根部的轴压载荷基本相同。地面试验时伸展机构除受端部施加的轴向载荷外，还有自身重力产生的均布载荷。随着伸展机构高度增加，伸展机构两端的载荷差异趋于明显，试验获得的屈曲承载能力将小于实际在轨承载能力，影响地面试验的有效性。对重力诱发的稳定性问题进行了一定的研究，文献[7]研究了竖立、水平放置悬臂梁在均布载荷作用下的后屈曲问题；文献[8]研究了细长梁在均布力和集中力共同作用下的后屈曲问题；文献[9]用有限元法对等曲率有重钻柱屈曲过程进行了分析，力学模型中考虑了重力；文献[10]用瑞利-里兹法对闭口薄壁桥墩进行分析，并导出了自重下桥墩的稳定性计算公式。上述文献中的研究对象多为梁柱结构，从理论角度进行研究，未深入涉及工程结构和试验。伸展机构展开长度可达数十米，是典型的细长结构，屈曲试验中自身重力诱发的屈曲问题虽未见研究，但非常值得关注。本文将伸展机构简化为悬臂梁，分析了集中载荷与均布载荷共同作用下梁的屈曲问题。以盘绕式伸展机构为例，针对其非线性特点，采用弧长法对比分析了不同尺寸伸展机构在空间与地面环境中的屈曲，以供伸展机构仿真与地面试验参考[11-12]。

1 理论计算

根据伸展机构的边界条件，可将其简化为根部固支和端部自由的悬臂梁模型，梁受均布力q，如图1所示。

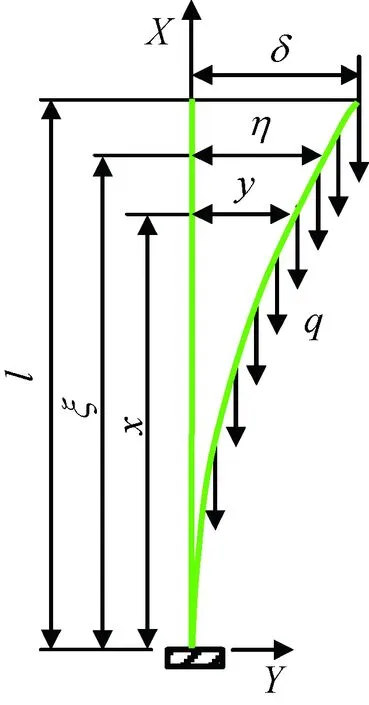
图1 均布载荷梁模型Fig.1 Uniformly distributed load beam

悬臂梁的临界载荷可用能量法求解。对梁的挠曲线方程采用三角级数近似

式中：δ1，δ2为三角级数的系数[12]。

任意截面的弯矩和弯曲应变能分别为

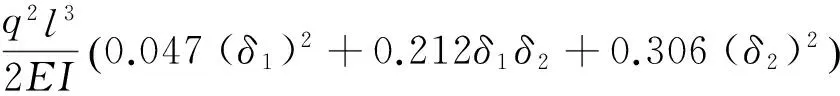
式中：E为材料弹性模量；I为弯曲惯性矩。

均布载荷所作的功为

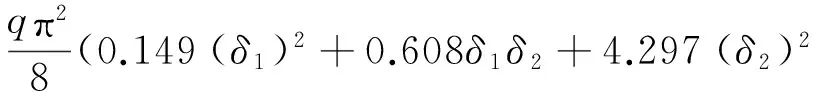
当ΔU=ΔT时可得结构失稳的临界载荷

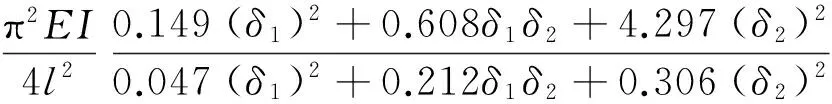
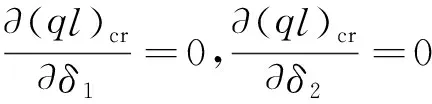
0=

则可得

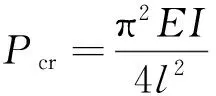
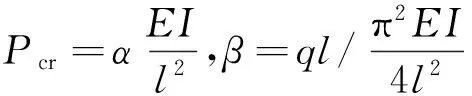
(1)

式(1)可用Bessel函数法计算。对不同的β值，可得对应的α值见表1，如图2所示。

表1 α与β对应关系

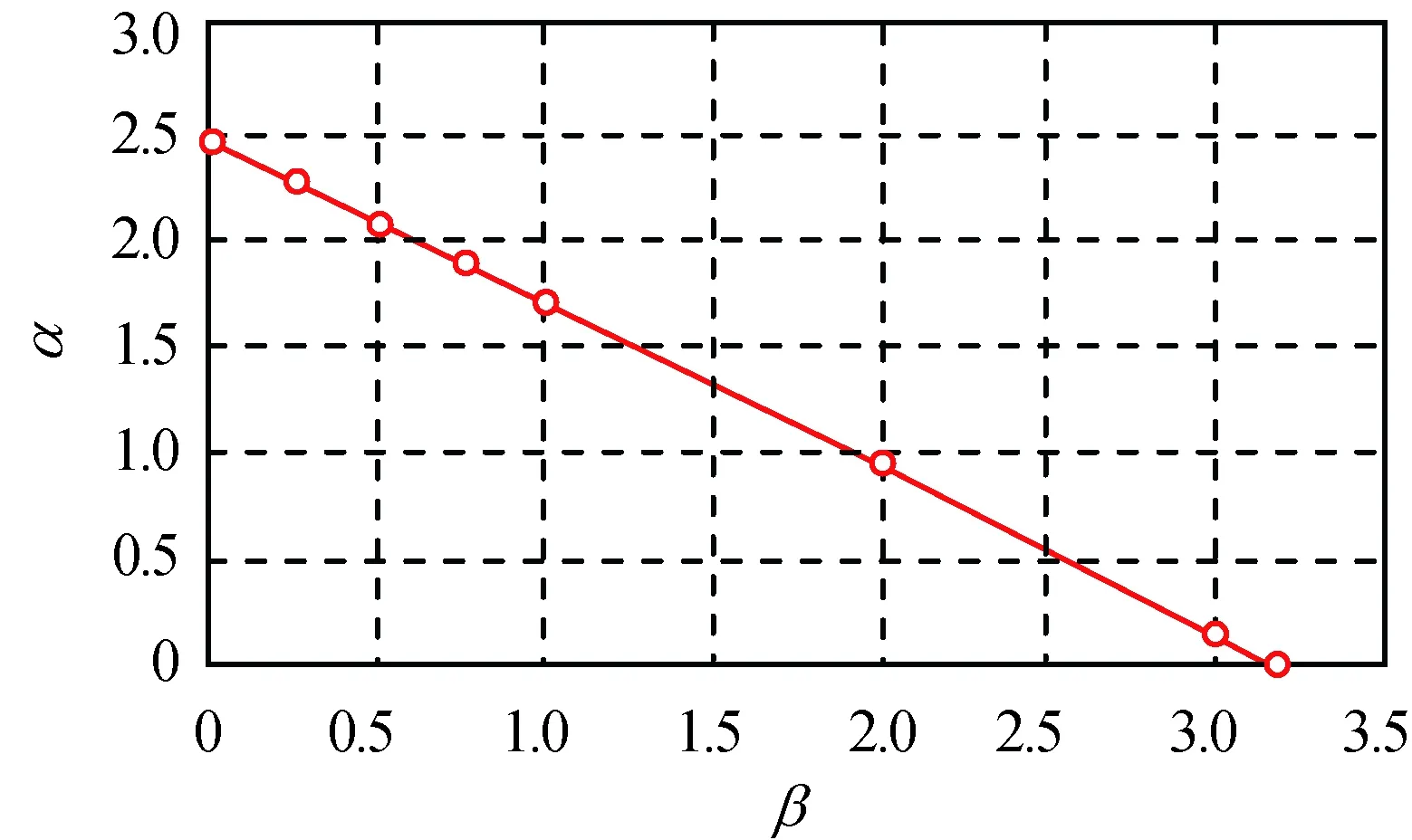
图2 α-β曲线Fig.2 α-β curve

图2表明：β，α近似呈线性关系，有α=π2/4-0.78β。因此对悬臂梁来说，均布载荷ql的影响相当于在梁的端部施加0.32ql的集中载荷，即在集中载荷与均布载荷共同作用下的轴压屈曲临界载荷可近似为

(2)

式(2)表明重力在一定程度上降低了伸展机构的承载能力。可预见当伸展机构越长，其影响越明显。

2 有限元分析建模

根据线性梁理论进行的理论推导，在研究伸展机构的稳定性时还需考虑钢丝绳松弛和机构大变形产生的几何非线性影响。为研究重力对伸展机构的非线性屈曲的影响，本文用有限元法进行建模分析。

伸展机构有限元建模时，纵杆和横框选用梁单元，纵杆与横框间不存在相对转动自由度，两者采用共节点的连接；纵杆和横框的材料为玻璃纤维，弹性模量50 GPa，泊松比0.3。伸展机构的对角张紧拉索只能受拉，不能受压，在受力过程中部分拉索松弛，部分拉索将进一步张紧，此时伸展机构刚度与初始状态相比将有很大改变。为准确描述钢丝绳的力学行为，用非线性弹簧单元模拟，定义弹簧的受压刚度为0，受拉刚度为1 000 N/mm(试验测得)，则可得弹簧位移-力曲线如图3所示。其中，0位移下的纵坐标值为对角拉索的初始预紧力。

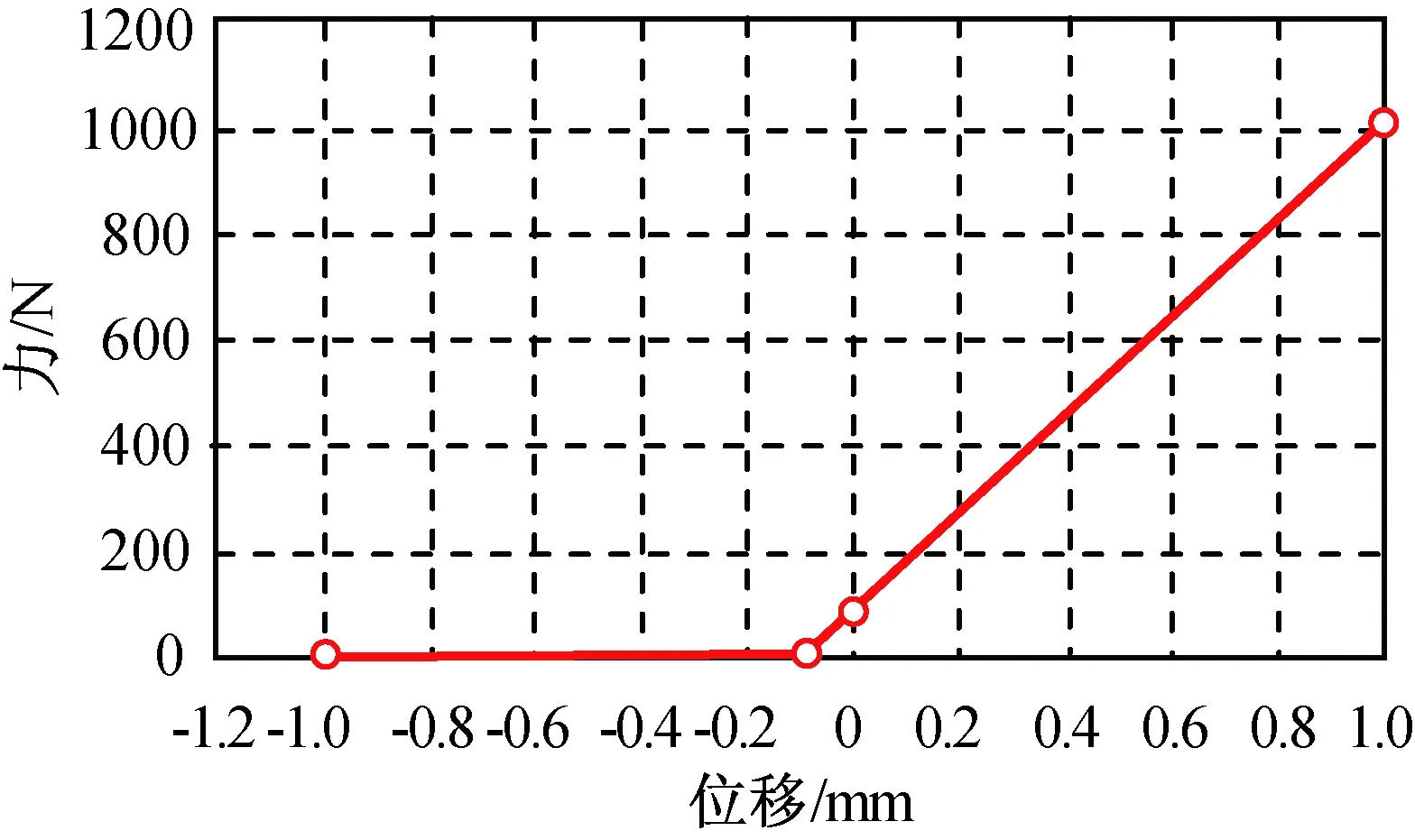
图3 非线性弹簧的力-位移曲线Fig.3 Force-displacement curve of nonlinear spring

因特征值法无法有效求解伸展机构的非线性屈曲问题，本文用Abaqus中的弧长法进行求解[13]。计算分两步：第一步对伸展机构施加重力载荷，计算静态非线性；第二步用特征值法获取伸展机构的线性屈曲模态，并将其作为初始缺陷引入弧长法计算中，获取伸展机构的屈曲承载能力。伸展机构的有限元模型(部分)如图4所示。

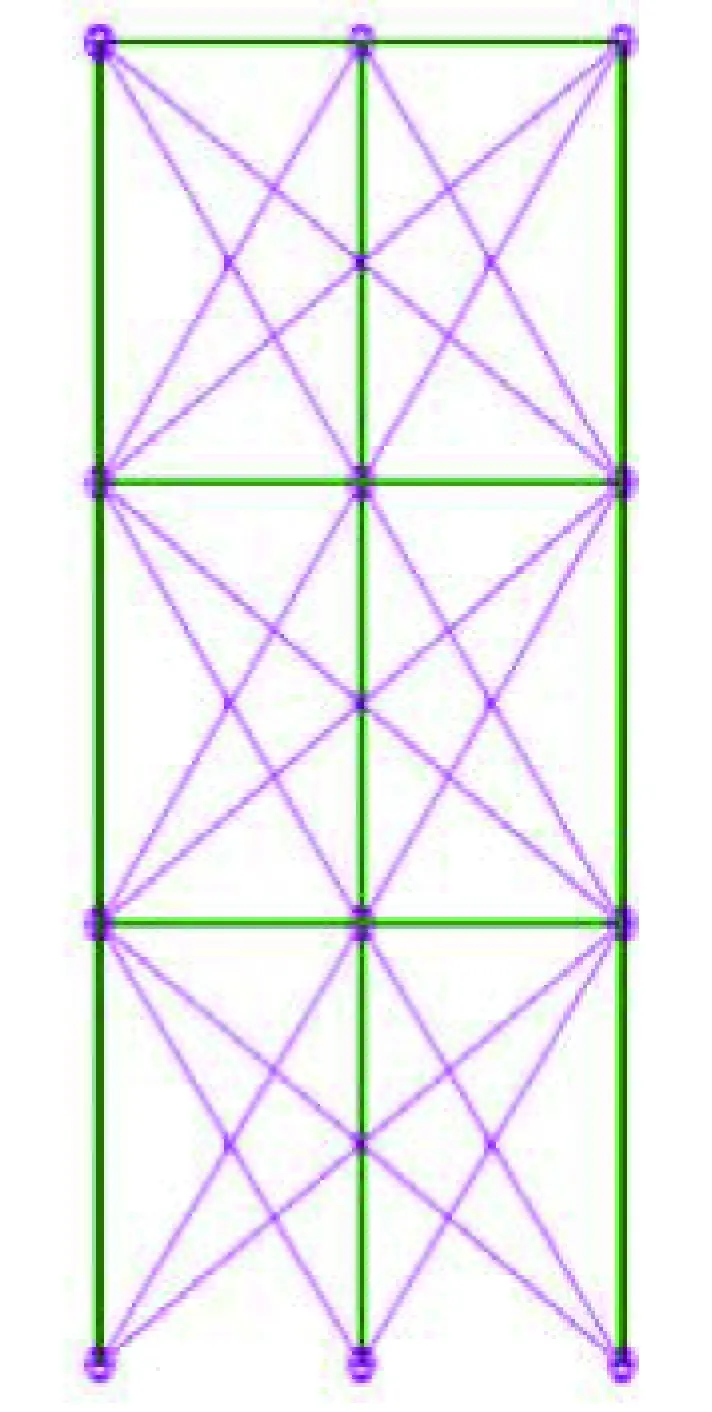
图4 3节伸展机构有限元模型Fig.4 3-bay finite element model of coil-able mast

分别计算14，30 m两种尺寸伸展机构轴压稳定性，分析地面试验环境和空间环境中伸展机构轴向屈曲。其中：14 m伸展机构质量约11.6 kg；30 m伸展机构质量约25.1 kg。

用弧长法分析非线性屈曲，增量迭代方程为

KTΔu=ΔλP+R.

式中：KT为切线刚度；Δu为节点位移增量；Δλ为载荷因子；P为参考载荷向量；R为残余力向量。

为匹配未知数与方程数，还需增加约束方程

(Δu)TΔu+(Δλ)2(ΔP)TΔP=(Δl)2.

式中：Δl为弧长增量。

对上述增量方程进行迭代求解，直至ΔλP+R在允许的范围内。当结构的|KT|>0时，结构位移随载荷增加而增大；当|KT|<0时，结构载荷随位移增加而减小；当|KT|=0时，载荷出现极值点即为结构的屈曲载荷。

3 试验验证与结果分析

为验证伸展机构非线性屈曲分析的正确性，对14 m的伸展机构进行了轴压屈曲试验。试验时，伸展机构末节固定于底部工装，通过底部工装的周向螺栓将其固定于试验台上，伸展机构头部横框与顶盘连接，通过顶盘的加载孔悬下足够长度的钢丝绳，钢丝绳与地面液压缸相连，通过液压缸将轴压作用力施加到加载盘上。试验方案如图5所示。试验中在载荷加载至1 465 N时，伸展机构出现垮塌，无法继续加载，并伴有典型的欧拉屈曲特征。

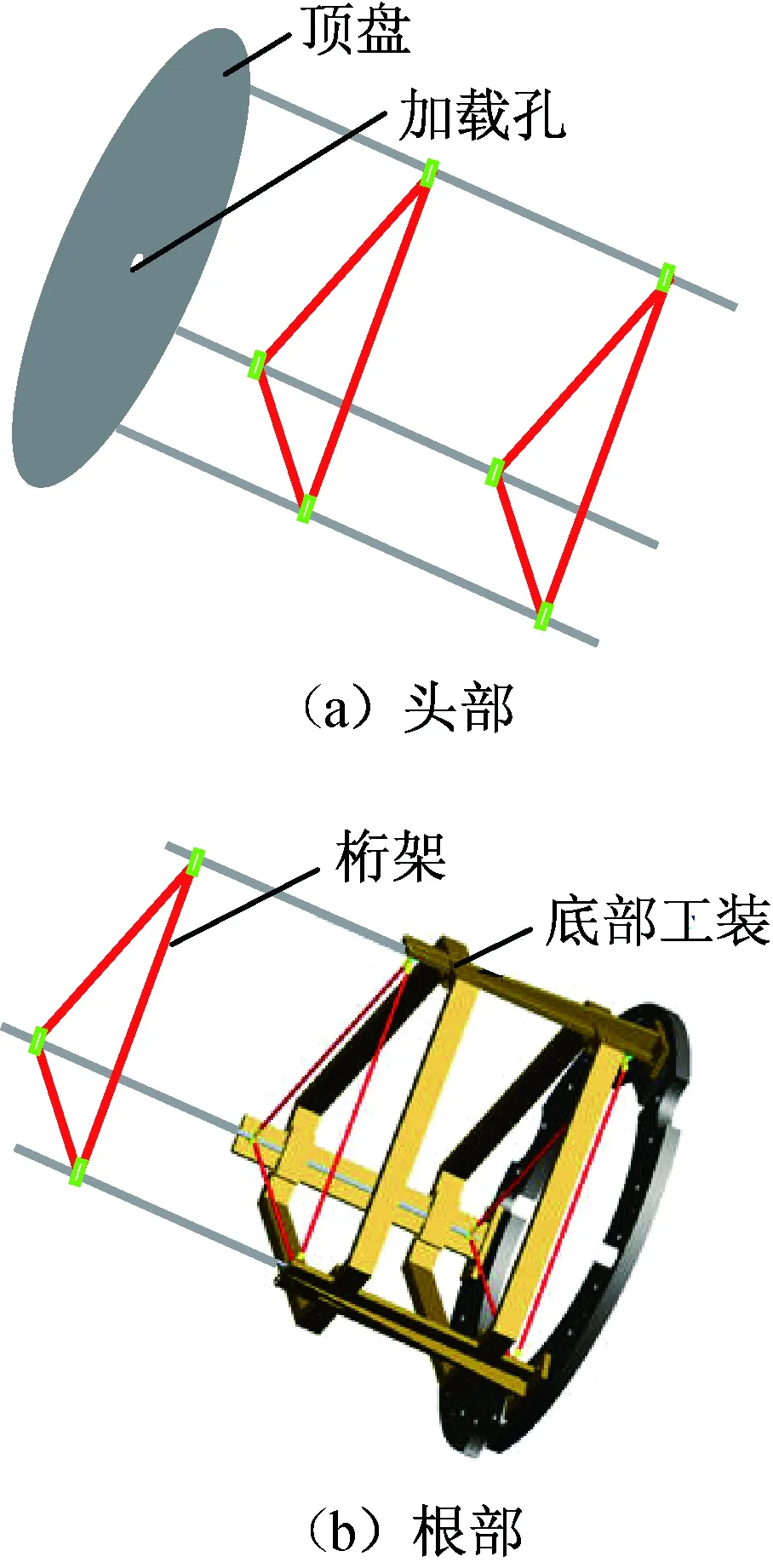
图5 14 m伸展机构头部与根部状态Fig.5 Experimental status of 14 m coil-able mast

仿真所得该伸展机构的轴压屈曲载荷曲线如图6所示。表明空间环境中伸展机构的轴压屈曲载荷为1 542 N，地面试验环境中屈曲载荷1 501 N，两者相差41 N，14 m伸展机构的质量11.6 kg，差值约为重力的0.34倍。伸展机构试验和仿真的屈曲模态如图7所示。屈曲载荷的地面试验值1 465 N，考虑重力与否均得到了与地面试验一致的模态和结果，这是由于重力仅为伸展机构屈曲载荷约8%，重力的影响可不考虑。此外比较试验与计算结果表明：用弧长法算得的伸展机构非线性屈曲正确。

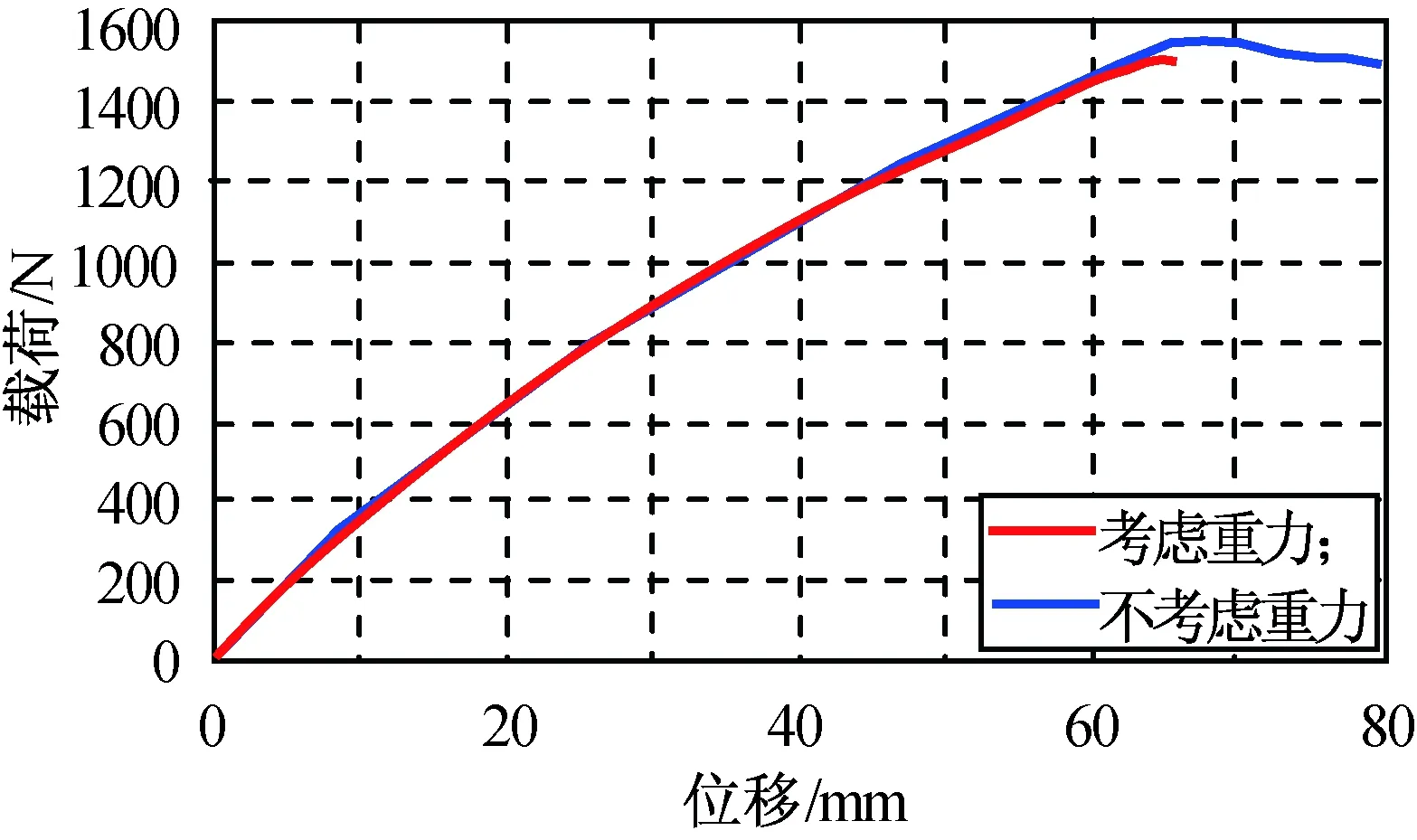
图6 14 m伸展机构轴压屈曲载荷Fig.6 Buckling load of 14 m coil-able mast

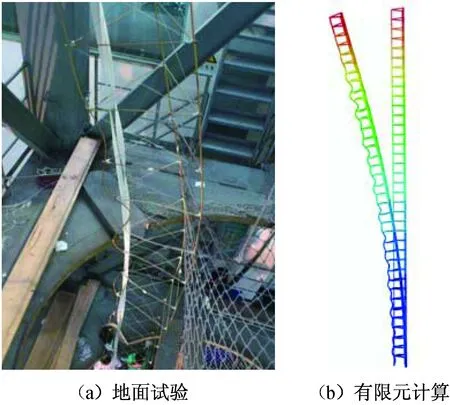
图7 14 m伸展机构屈曲模态Fig.7 Axial compression buckling mode

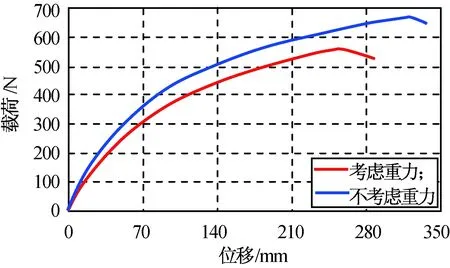
图8 30 m伸展机构轴压承载能力Fig.8 Buckling load of 30 m coil-able mast

计算30 m伸展机构的轴压屈曲，所得轴压屈曲载荷如图8所示。仿真表明：空间环境中伸展机构的轴压屈曲载荷669 N，地面环境伸展机构屈曲载荷561 N，两者相差约100 N，约为重力的0.4倍，大于理论推导的0.32倍。分析认为这是由伸展机构的几何非线性造成的。随着伸展机构高度和质量的增加，重力对伸展机构承载能力的影响也趋于明显，此时在地面试验中必须考虑重力因素。

通过上述两种尺寸伸展机构的轴压承载能力计算，在不考虑伸展机构非线性情况下，可采用试验载荷加0.32倍重力进行修正。

4 结束语

本文对伸展机构地面屈曲试验的重力影响及修正方法进行了研究，给出了悬臂梁模型并进行了理论计算，建立了有限元模型，讨论了重力对14，30 m两种伸展机构非线性屈曲的影响。研究发现地面环境中伸展机构的屈曲载荷低于空间环境。随着伸展机构高度和质量的增加，两者相差趋于明显。在地面试验中必须考虑重力对试验有效性的影响，对试验值进行修正。理论计算表明均布载荷ql可近似考虑为0.32ql的集中载荷。由于伸展机构的几何非线性原因，数值计算获得的重力等效因子略大于0.32。但从保守角度考虑，伸展的在轨承载能力可按地面试验值加0.32倍重力进行修正。该方法为其它同类机构的地面试验及修正提供了参考依据。

[1] KITAMURA T, YUMASHIRO K, OBATA A, et al. Development of a high stiffness and retractable mast “HIMAT” for space applications: 31stAIAA/ASME-ASCE /AHS/ASC Structures, Structural Dynamics and Materials Conference[C]// Long Beach: AIAA, 1990.

[2] LAKE M S. Mechanism design principle for optical-precision deployable instruments[R]. AIAA, 2000-1409, 2000.

[3] TAKAYUKI K, KAKUMA O. Development of a “Hingeless Mast” and its application[J]. Acta Astronautica, 1998, 17(3): 341-346.

[4] EIDEN M, BRUNNER O, STAVRINIDIS C. Deployment analysis of the Olympus astromast and comparison with test measure-elements[J]. Journal of Spacecraft and Rockets, 1987, 24(1): 63-68.

[5] 刘涛, 金玉龙, 吕榕新, 等. FASTMast伸展机构屈曲模式的理论分析与试验[J].宇航学报, 2015, 36(4): 404-409.

[6] 孙宏丽, 张少伟, 谭天乐. 航天器可展附件展开动力学建模研究[J]. 上海航天， 2015， 32(1)： 1-4.

[7] FRISCH-FAY R. The analysis of a vertical and horizontal cantilever under a uniformly distributed load[J]. Journal of the Franklin Institute, 1961, 271: 192-199.

[8] VAZ M A, MASCARO G. H W. Post-buckling analysis of slender elastic vertical rods subjected to terminal forces and self-weight[J]. International Journal of Non-Linear Mechanics, 2005, 40(7): 1049-1056.

[9] 刘峰, 王鑫伟. 等斜率井中有重钻柱屈曲的非线性有限元分析[J]. 力学学报, 2005, 37(5): 593-599.

[10] 白青侠, 郝宪武. 考虑重力条件下高薄壁桥墩弹性稳定性分析[J]. 西北建筑工程学院学报(自然科学版), 2001, 18(1): 37-41.

[11] CRISFIELD M A. A fast increamental interative solution procedure that handles “snap-through”[J]. Computers and Structures, 1981, 13(1-3): 55-62.

[12] 叶康生, 吴可伟. 空间杆系结构的弹塑性大位移分析[J]. 工程力学, 2013, 30(11): 1-8.

[13] 铁摩辛柯S P, 盖莱J M. 弹性稳定性理论[M]. 北京: 科学出版社, 1985: 107-114.

Study of Gravity Effects on Ground Experimental Buckling of Deployable Truss Structure and Its Correction Methodology

LIU Tao1, 2, HAN Han2, TANG Guo-an1, CUI Qi-feng2, XIAN Kui-cheng2, PENG Zhi-long2

(1. Department of Aeronautics and Astronautics, Fudan University, Shanghai 200433, China; 2. Aerospace System Engineering Shanghai, Shanghai 201109, China)

According to the difference between the space environment and ground environment caused by gravity, the deployable truss structure was simplified as the cantilever beam with the fixed root and free end according to the boundary condition of the truss in this paper. The beam was forced by uniformly distributed load. The effects of gravity on the buckling of the cantilever beam were analyzed theoretically. The two finite element models of 14 and 20 m truss were established. The gravity was forced on the truss and the static nonlinearity was calculated. The modular of nonlinear bucking of the truss obtained by eigenvalue method was introduced into arc-length method to solve the bucking ability of the truss. The analysis result shows that the ground experimental result must be corrected when the truss reaches a certain height and the gravity will be equivalent to 0.32 times the concentrated load applied to the head of the truss. The study will provide some valuable information for studying other similar structures in future.

Deployable truss structure; Gravity; Buckling; Arc-length method; Uniformly distributed load; Concentrated force load; Ground test; Correction methodology

1006-1630(2016)05-0012-05

2015-11-19；

2016-01-27

国家自然科学基金资助(11202052)

刘 涛(1987—)，男，博士生，主要研究方向为柔性结构的非线性力学计算。

TU311.3

A

10.19328/j.cnki.1006-1630.2016.05.002