超隔热材料理论探究

冯仕猛,罗乾杰,刘嘉欣,顾琳慧,唐晓峰,张 红

(1.上海交通大学 物理与天文系,上海 200240; 2.上海航天技术研究院,上海 201109;3.上海机电工程研究所,上海 201109)



超隔热材料理论探究

冯仕猛1,罗乾杰1,刘嘉欣1,顾琳慧1,唐晓峰2,张 红3

(1.上海交通大学 物理与天文系,上海 200240; 2.上海航天技术研究院,上海 201109;3.上海机电工程研究所,上海 201109)

为新型超隔热材料研究提供理论依据，给出一种超材料简单结构模型，根据原子振动波传播的基本理论，用转移矩阵理论和不同区间边界上应力，以及振幅连续关系推导出超材料中声子的本征方程。它清楚表明了声子频率与原子层结构参数及特性参数的非线性关系。讨论了不同条件下声子的模数与频率，给出了两种特定条件下的初步解。初步解表明：不同的原子层结构设计，声子频率不同，声子振动模数也不同。只要选择合适的原子层结构，就能降低声子振动模数和调节声子振动频率，从而降低材料热传导系数。对某些特定设计的超级材料，有不存在声子振动模的可能，这样的材料不能传播热声子，也就不能有效传递热量，这对新型隔热材料研究是非常有意义的。

超材料； 矩阵理论； 声子； 本征方程； 原子层结构； 振动模； 热传导系数； 绝热

0 引言

热防护技术是保证航天器在上升段和再入段的外部加热环境中不发生过热和烧毁的一项关键技术，同时也是保证导弹在气动加热环境中正常工作和保证火箭发动机在严酷的内部加热环境中正常工作的一项关键技术。传统的隔热材料以陶瓷复合材料为基础(氧化硅纤维+硼化物+碳化硅)，再添加其它化合物以实现低热传导隔热材料，在航天器上获得了广泛应用[1-7]。如航天飞机上大量使用的陶瓷纤维隔热瓦由68%石英纤维(直径1～3 μm)+12%硼硅酸盐纤维(1～3 μm)+20%氧化铝纤维(5～10 μm)组成(质量分数)，是一种非常好的隔热材料；以SiC为添加剂料+高温的陶瓷ZrB2隔热材料，使导弹在飞行过程中能长时间承受3 000 ℃的高温，另外也有其它材料作为高速飞行器隔热材料的探索试验[8-9]。这些研究以大量实验为基础，通过材料配比优化实现其优异的隔热性能。超材料是一种新型材料，通过人工组装，有效调控原子层数，调控原子的种类，实现材料性能的有效调控。但超级材料研究主要集中于反常电磁性能，大多讨论介电常数呈负的材料理论和实验研究[10-17]。通过精确设计材料的结构，能对相对介电常数和有效相对磁导率进行控制。如超材料的质量密度或体积模量两者之一是负数，构造的超材料就是一种类似声子晶体的带隙材料，可阻挡声音的传播[18]。若质量密度和弹性模量同时为负数，则此人工超材料是一种双负材料，能实现材料的负折射[19]。上述研究多涉及材料电磁参数的理论处理或器件的模拟设计，但关于超隔热材料性能的研究很少。

理想的绝热材料，即完全隔热材料是目前超高速飞行器研究中的一个热点[20-21]。对实现材料的完全隔热，使热量无法在材料中传播，目前尚无完整的机理描述，相关的基本理论研究报道很少。材料的热传递是以原子热振动或声子传播为基础，如能使材料无法传播热声子，就可实现材料的理想化绝热。本文试建立一种超级材料的结构模型，根据原子振动的动力学方程，由热振动在边界上的连续条件和矩阵理论给出了热声子在材料中传播的本征方程，分析了不同条件下声子振动频率与超级材料原子结构参数的关系，讨论不同条件下传播热声子的模数和频率，并在此基础上给出了降低材料热传导可能的物理途径，以拓宽研究新型隔热材料的理论思路。

1 新型材料热传导的基本理论

热在材料中传播，一种模式是通过红外电磁波透过材料而传递热量，另一种方式是通过材料中原子振动传播热量，即依靠声子传播热量。超材料可通过在材料的关键物理尺度上的有序设计，有效控制原子振动频率，减小声子的振动模数，从而使材料导热系数降低，达到隔热效果。

本文设计一种简单的超级材料结构模型：由甲乙两种不同的原子在一维方向上呈周期性排列。其中甲原子的原子层数为N1，乙原子的原子层数为N2，其结构如图1所示。

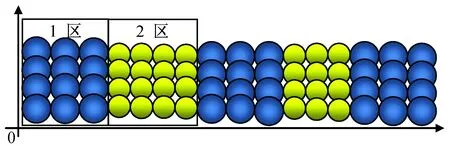
图1 一种简单的超级材料结构模型Fig.1 Simple model of metamaterial

在图1模型中，设甲原子构成的区间定为1区，乙原子构成的区间为2区。根据原子振动波方程，在1、2区间内，其对应原子振动波方程分别为

(1)

式中：A1，A，A′，B，B′为波方程的系数；y0，y1，y2，y3为不同区间原子振动的振幅；N为超材料中周期层数；q1，q2分别为区间1、2波方程对应的波矢；ω为离子或原子的振动频率；a为1区N1个原子构成的长度；b为2区N2个原子构成的长度；β′为波在边界上的衰减系数；i为虚数单位。

在1区间，成立

(2)

(3)

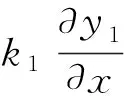
(4)

用相同方法，可得x=a处有

(5)

由式(5)可得

(6)

式(6)的矩阵形式为

(7)

将式(7)代入式(4)，有

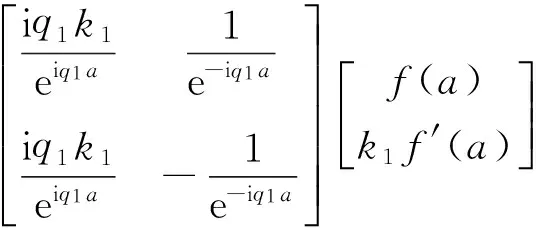
(8)

简化式(8)，可得

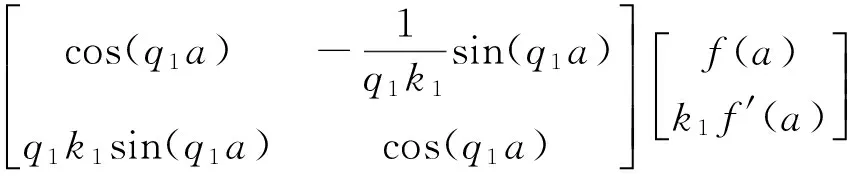
(9)

用相同方法，在2区可得

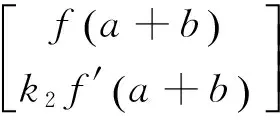
(10)

式中：k2为2区对应材料的弹性模量；k2f′(a)为b区x=a处的应力。

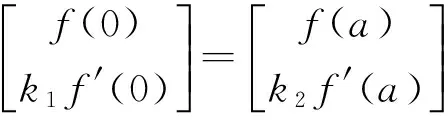
(11)

对由N个周期层构成的超级材料，则有

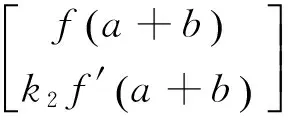
(12)

展开式(12)，有

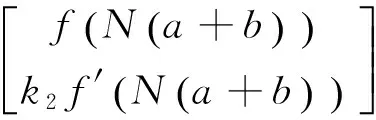
(13)

式中：

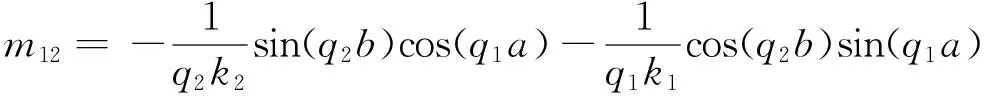
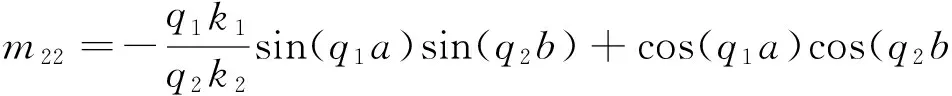
在材料表面，由式(1)分别可得

a)x≤0时，

(14)

b)x≥l时，

(15)

式中：l，k′分别为超级材料的宽度和表面弹性系数。将式(14)、(15)代入式(13)得

(16)

(17)

用多项式可得

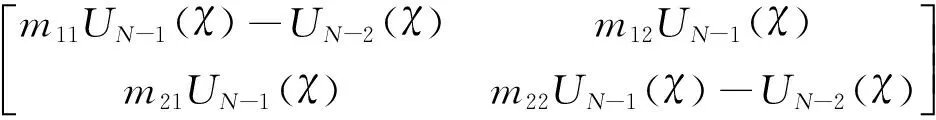
(18)

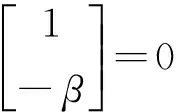
(19)

式(19)即为研究超材料的基础方程。

2 讨论

2.1 超材料性能与空间尺寸关系

将式(19)展开后得

2βUN-2(χ)+m21UN-1(χ)-βm11UN-1(χ)+

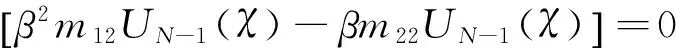
(20)

化简式(20)得

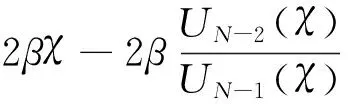
(21)

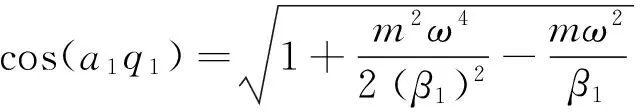
式中：a1为1区相邻两个原子间的距离；m为1区原子质量；β1为1区原子间的弹性系数；ω为原子振荡频率。代入式(21)，得

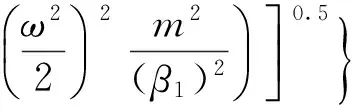
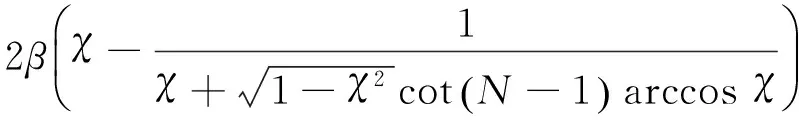
(22)

式中：b1为2区相邻两个原子间的距离；M为2区间原子质量；β2为2区间原子间的弹性系数；N2为1区原子的层数；N2为2区原子的层数；N为总周期数。

式(22)是超级材料中热声子的本征方程，满足该式频率的声子才能在超级材料中传播。由式(22)可知：超级材料中原子的振动频率不仅与材料本身的性质有关，而且与原子层数结构参数有关。不同的材料组合，传播声子的振动频率各异；在材料组合确定的条件下，原子层数结构参数不同，声子频率也不同。因此，理论上仅需调节1区和2区原子的结构参数，就能控制声子振动模数及频率，这是调节超级材料性能的物理基础。

2.2χ=0的超级材料

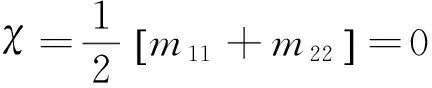
tan(q1a)tan(q2b)=

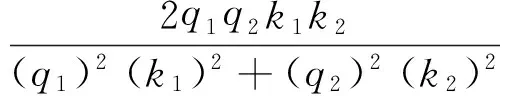
(23)

将χ=0 代入式(18)，展开得

-βm11+m21+β2m12-βm22=0.

(24)

将 m11,m21,m12,m22代入式(24)，化简得

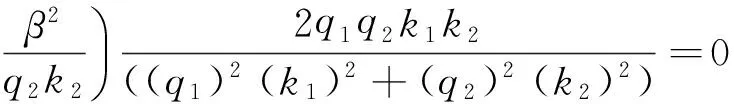
(25)

则

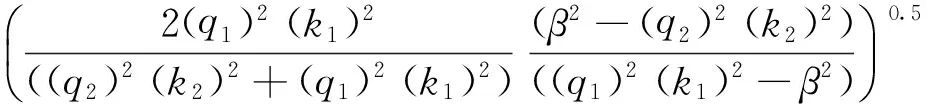
(26)

代入式(26)，得

(27)

或

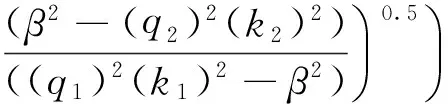
(28)

同理，由式(23)、(25)还可得

(29)

或

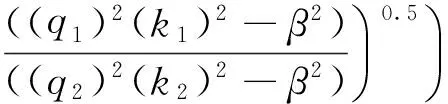
(30)

对χ=0的超级材料，其原子振动频率必须同时满足式(28)、(30)。由式(28、(30)可知：原子振动频率与材料本身的性质、原子结构参数呈明显的非线性关系，不同尺寸的超级材料有不同的原子振动频率。因此，只需优化1、2区原子层结构参数，就能降低声子的振动模数，这对降低材料热传导系数非常有用。

特别是当χ=0，如β2-2(q2)2(k2)2<0或(q1)2(k1)2-β2<0，则式(28)、(30)中根号内为虚数，这表明满足本征方程的频率存在一个虚数，也就是不存在能传播的热声子。因此，只要材料表面弹性系数非常大或非常小，对应的材料无法传播热声子，使这种材料的导热系数非常低，理论上这是一种非常好的绝热材料。因此，若技术上能实现上述条件的原子排列，则能获得导热系数非常小的隔热材料。

2.3χ=1的超材料

当χ=1, 由式(18)得

2β+m21-βm11-βm22+β2m12=0.

(31)

将 m11,m21,m12,m22代入式(31)，化简得

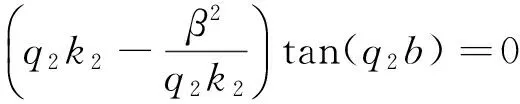
(32)

代入式(32)，得

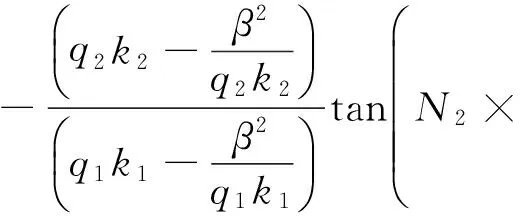
(33)

或

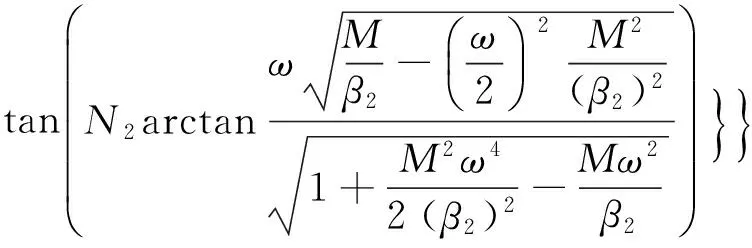
(34)

式(34)是满足χ=1的超级材料热声子传播的本征方程。由式(34)可知：声子频率与原子层结构参数间呈非线性关系；不同材料的组合，热声子频率各异，声子振动模数亦不同；在材料组合确定条件下，原子层结构参数不同，声子振动频率和振动模数也不同。

特别地，当N1≫N2，由式(34)可得

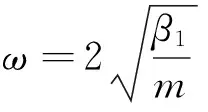
满足该条件的材料只能传播一种频率的声子，这会使该种材料导热性能非常低，这对未来超低导热材料的研究非常有意义。

综上所述，对超级隔热材料，通过一定的技术方法实现不同原子有规律的组装，就能有效控制声子的振动频率和声子的振动模数。在满足一定的条件下，可获得非常少或为零振动模的超材料，其对应的导热率就非常低，这是将来弹头隔热材料研究发展的一个方向。

3 结论

本文通过一个不同材料在空间有规律排列的模型，利用物理原理推导了超隔热材料传导的本征方程，给出了两种典型结构的超材料本征方程的初步解，分析了对应声子振动模数及频率与结构参数间的关系，获得了一些初步结论：超材料中声子频率及模数与原子层结构设计参数呈非线性关系。不同原子层结构设计，声子频率和声子振动模数不相同。对某种特殊设计的超隔热材料，可使超材料的本征方程无解，也就不存在能传播的热声子。因此，这样的材料导热系数非常低，理论上是一种非常好的绝热材料。传统以陶瓷复合材料为基础的隔热材料，实际上是多种材料的混合体，材料空间结构缺少规律性，需要大量的实验才能找到性能较好的隔热材料。未来超隔热材料的研究，理论上需确定多种原子排列的结构模型，再通过一定的技术方式实现两种或两种以上不同原子有规律的组装，才能有效控制声子的振动频率与模数，甚至使声子振动模数趋向零和使材料导热系数降至一个非常低的水平，从而实现最佳的隔热或绝热效果，这是未来弹头以及超高声速飞行器超隔热材料研究发展的一个方向。本文研究对高速飞行器的新型隔热材料研制有一定的参考意义。

[1] 吴江. 飞航弹道热防技术发展趋势[J]. 强度与环境, 2009, 36(1): 57-63.

[2] 刘海鑫, 徐戈, 丁尚宗. 导弹弹头防热技术初探[J]. 复合材料, 2008(S1): 69-72.

[3] RIVERS H K, SIKORA J G, SANKARAN S N. Detection of hydrogen leakage in a composite sandwich structure at cryogenic temperature[J]. Journal of Spacecraft & Rockets, 2002, 39(3): 452-459.

[4] HANK J, MURPHY J , MUTZMAN R. The X-51A scramjet engine flight demonstration program[R]. AIAA, 2008-2540, 2008.

[5] 李俊宁, 胡子君, 孙陈诚, 等. 高超声速飞行器隔热材料技术研究进展[J]. 宇航材料工艺, 2011, 41(6): 10-13.

[6] 洪流, 石晓波, 张峰. 隔热罩对火箭发动机推力室温度场的影响[J]. 上海航天, 2009, 26(4): 47-51.

[7] 王钦, 胡子君, 孙陈诚, 等. 陶瓷隔热瓦力学性能影响因素及其稳定性控制[J]. 宇航材料工艺, 2010, 40(2): 77-79.

[8] 鲁芹, 胡龙飞, 罗晓光, 等. 高速飞行器复合材料与热结构研究进展[J]. 硅酸盐学报, 2013, 41(2): 251-260.

[9] 虞红. 软木作为火箭隔热材料的研究[J]. 上海航天, 1996, 13(5): 54-56.

[10] FANG N, XI Dong-juan, XU Jian-yi, et al. Ultrasonic metamaterials with negative modulus[J]. Nature Material, 2006, 5(6): 452-460.

[11] LAI Yun, WU Ying, SHENG Ping, et al. Hybride lastic solids[J]. Nature Material, 2011, 10(8): 620-624.

[12] WU Ying, LAI Yun, ZHANG Zhao-qing. Elastic metamaterials with simultaneously negative effective shear modulus and mass density[J]. Physical Review Letter, 2011, 107(10): 232-234.

[13] MEI Jun, MA Guan-cong, YANG Min, et al. Dark acoustic metamaterials as super absorbers for low-frequency sound[J]. Nature Communications, 2012, 3(2): 132-136.

[14] MEI Jun, YANG Min, YANG Zhi-yu, et al. Membrane-type acoustic metamaterial with negative dynamic mass[J]. Physical Review Letters, 2010, 101(20): 2952-2965.

[15] LAI Yun, WU Ying, SHENG Ping, et al. Hybrid elastic solids[J]. Nature Materials, 2011, 10(8): 620-624.

[16] SONG J Z, BAI P, HANG Z H, et al. Acoustic coherent perfect absorbers[J]. New Journal of Physics, 2014, 16(3): 1-9.

[17] BLIOKH Y P, BRODSKY Y L, CHASHKA K B, et al. Broad-band polarization-independent absorption of electromagnetic waves by an overdense plasma[J]. Physics of Plasmas, 2009, 17(8): 585-591.

[18] WU Y, LAI Y, ZHANG Z Q. Effective medium theory for elastic metamaterials in two dimensions[J]. Phys Rev B, 2007, 76(20): 205313-205318.

[19] WU Ying, LAI Yun, ZHANG Zhao-qing. Elastic metamaterials with simultaneously negative effective shear modulus and mass density[J]. Pphysical Rreview Letter, 2011, 107(10): 232-234.

[20] 杨杰, 隋学叶, 刘瑞祥, 等. 航天飞机以及高速飞行器隔热材料研究进展[J]. 现代技术陶瓷, 2015(3): 25-29.

[21] 王璐, 王友利. 高超声速飞行器热防护技术研究进展和趋势分析[J]. 宇航材料工艺, 2016, 46(1): 1-6.

Theoretical Investigation of Insulation Heat Property of Super-Material

FENG Shi-meng1, LUO Qian-jie1, LIU Jia-xin1, GU Lin-hui1, TANG Xiao-feng2, ZHANG Hong3

(1. Department of Physics and Astronomy, Shanghai Jiao Tong University, Shanghi 200240， China; 2. Shanghai Academy of Spaceflight Technology, Shanghai 201109, China; 3. Shanghai Electromechanical Engineering Institute, Shanghai, 201109, China)

For the study of super-material theory, a simple model of super material was presented. According to the basic theory of mechanical wave propagation, using the transfer matrix and continuous stress and amplitude at the different boundary, one eigenequation of phonon was derived which clearly described the nonlinear relationship of phonon frequency with the designed parameters of atomic layer structure and the property parameter of material. The modular and frequency of phonon were discussed under various conditions. The preliminary solution of the equation was given under two specific conditions. The preliminary solution shows that the phonon frequency changes with the change of the design of atomic layer. Generally, the phonon frequency and the number of phonon vibration mode would be different when the structure parameter of atomic layer is different. It can reduce phonon frequency and the number of phonon vibration module as long as choosing appropriate atomic layer structure, which leads to the low coefficient of thermal conductivity. Especially, for specific design of the super material, it may have no phonon vibration mode, and can't spread thermal phonons. That is to say, it will not be able to transfer heat efficiently. This new type insulation material is very significant for the research of new heat insulation materials.

Super-material; Matrix theory; Phonon; Eigenequation; Atomic layer structure; Vibration mode; Coefficient of thermal conductivity; Heat insulation

1006-1630(2016)05-0050-07

2016-07-12；

2016-08-07

冯仕猛(1964—)，男，博士，主要从事新颖材料物理研究。

TB34

A

10.19328/j.cnki.1006-1630.2016.05.008