基于压电作动器的空间单轴主动隔振研究

邱 炜,朱庆华,李结冻,施桂国

(1.浙江大学 控制科学与工程学院,浙江 杭州 310027; 2.上海市空间智能控制技术重点实验室,上海 201109; 3.上海航天控制技术研究所,上海 201109)



基于压电作动器的空间单轴主动隔振研究

邱 炜1,朱庆华2、3,李结冻2、3,施桂国2、3

(1.浙江大学 控制科学与工程学院,浙江 杭州 310027; 2.上海市空间智能控制技术重点实验室,上海 201109; 3.上海航天控制技术研究所,上海 201109)

对六自由度空间Stewart隔振平台中基于压电作动器的单轴主动隔振进行了研究。提出了三类标准以衡量隔振性能，其中：第Ⅰ类为载荷端与扰动端同量纲振动量比；第Ⅱ类为隔振后载荷端的受力与隔振前固连时载荷受力比；第Ⅲ类为隔振前后振动量的衰减状况。给出了压电作动器的基本方程，并根据实际进行了数值修正。建立了线性化的压电作动器单轴隔振系统，采用作动器的运动总与扰动端振动分量互补的主动隔振策略。讨论了速度反馈控制、力反馈控制与代数环引入，以及质量对隔振性能的影响。提出了隔振方向和隔振代价的概念。仿真结果表明速度反馈和力反馈均能获得较好的隔振效果。理论分析了隔振方向对隔振性能和隔振代价的影响。研究为空间Stewart隔振平台设计提供了理论支持。

六自由度空间Stewart隔振平台； 单轴主动隔振； 压电作动器； 隔振性能； 衡量标准； 速度反馈控制； 力反馈控制； 隔振方向； 隔振代价

0 引言

随着空间技术的进步，航天器的尺寸和结构不断向大型化、挠性化方向发展，导致航天器容易受激起振，同时有效载荷的功能逐渐复杂、敏感度提升，要求在超静力学环境中工作，因此航天工程对空间隔振技术的需求显得日益迫切。航天器的中高频微幅隔振大体可分为两类：一是对反作用飞轮、控制力矩陀螺群等振源设备进行隔振；二是对精密相机、激光通信设备等敏感载荷进行隔振[1-3]。主动隔振是一种有源隔振，通过引入次级可控振源，设计控制策略使传递到目标端的有害振动得到衰减[4]。目前，主动隔振技术总体上还处于研究阶段，实际应用较少，主要是因为：不同场合隔振需求的多样性，无统一的解决方案；难以找到同时具有宽频带和大输出能力(包括力和位移)的作动器；智能材料作动器的特性和控制有待研究；控制算法实现过程可能受硬件能力的限制[5-6]。本文以空间中单轴主动隔振为研究对象，对主动隔振的控制策略进行了研究，并讨论了质量对主动隔振效果的影响。

1 隔振衡量标准

在研究振动隔离问题时，应先确定描述隔振效果的衡量标准，也称隔振性能或振动衰减比，复频域中记为传递函数R(s)。本文研究空间中单轴微幅隔振，如图1所示。图中：x1，x2分别为两端的绝对位移；fd为施加在扰动端M1上的扰动力，载荷端M2与M1仅通过隔振元件连接，M2不受其他作用力；f01，f02为隔振元件产生的一对内部作用力，若隔振元件属轻质，则两者等大反向。

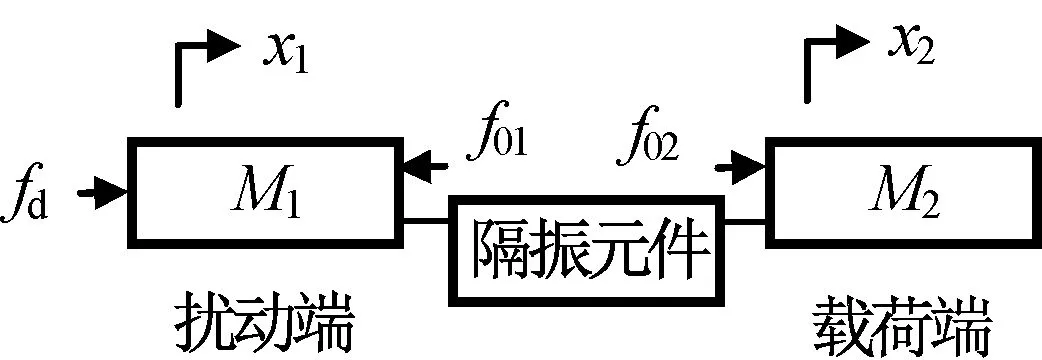
图1 空间单轴隔振Fig.1 Spaceborne single axis vibration isolation

本文提出以下三类隔振衡量标准。

a)第Ⅰ类：取载荷端与扰动端的同量纲振动量比为R(s)，有

(1)

式中：i=0，1，2，分别对应零初态的位移、速度和加速度；X1，X2分别为x1，x2的拉氏变换。注意RI(s)不以Fd(s)为分母，故非真实传递通道，仅是从相对运动角度反映隔振效果的一种数值关系。

b)第Ⅱ类：取隔振后作用于载荷端的f02与隔振前固连时的载荷受力对比，扰动力衰减比

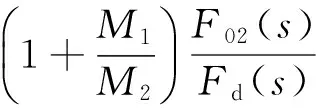
(2)

相比第Ⅰ类标准，RⅡ(s)与系统中一条真实传递通道仅增益系数有差别，故在主动隔振中还可判断闭环稳定性。

c)第Ⅲ类：对比隔振前后某个或某些振动量的衰减状况综合衡量隔振性能，是一种较灵活的标准。这非常适于含主动元件的隔振系统，比较主动控制切换前后系统中多个振动量的变化就可直观了解隔振系统的性能。但由于隔振前后非同一物理系统，不便给出解析形式的R(s)。

上述三类隔振衡量标准间不存在绝对的使用界限，从性能指标来看三者存在差异，主要表现为衰减程度和谐振峰特征不同。一般，第Ⅲ类最全面、灵活，第Ⅰ、Ⅱ类更注重隔振系统中的细节。

2 压电作动器建模

压电作动器基于逆压电效应工作，物理特性较复杂。作动器模型的真实程度直接关系隔振仿真效果。本文以压电理论为基础，结合产品级作动器的参数建立适用于研究的数值修正模型，提高仿真可靠性。

2.1 压电作动器基本方程

压电作动器由多片压电材料正反交替堆叠而成，以增大作动器行程。单片材料经不同方向极化对应不同的压电效应，其中d33效应可使产生的应力与施加电场同轴向，据此设计推拉式压电作动器[7-8]。根据压电理论可用电场强度E和电应变ε描述其电特性，d33效应的分量形式为

ε=d33E.

(3)

参数d33表示沿3号轴的电场对沿3号轴的应变量的压电应变常数。令单片压电材料的厚度为h，截面积为Ap，杨氏模量为Ep，共N片堆叠组成压电元件，作动器整体伸长量为Δx，电极电压为u，则由式(3)可得单片压电材料在形变截面上产生的应力

(4)

作动器对外输出力方向与应力相反，有

(5)

f(u,Δx)=Kvu-K0Δx.

(6)

式(6)即作动器静态模型。添加线性阻尼系数C0，可得动态模型

(7)

2.2 模型数值修正

真实作动器特性较复杂，对与理论模型偏差较大的两方面进行修正：一是推拉能力的不对称性，压电滞环效应导致作动器静态推力上限远大于拉力上限，而静态模型式(6)的推拉能力是对称的；二是作动器的等效电容[8]。压电作动器需由高压功率放大模块驱动，而作动器本身是典型的容性负载，故驱动电路中的RC惯性环节不可忽略。

作动器的数值修正以PI Ceramic公司针对主动隔振应用设计的P-844.10压电作动器为对象，其参数为：开环行程(0～100 V)(153) μm；刚度系数(22545) N/μm；推/拉力容量参考3 000/700 N；电容(6.01.2) μF；空载谐振频率(163.2) kHz；质量(844.2) g。用开环行程和刚度系数可确定理想静态力模型式(6)，由Sigmoid函数根据推拉力上限对其进行分段光滑限幅修正，有

fsta(u,Δx)=

(8)

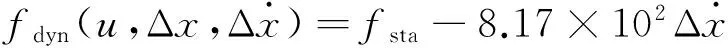
(9)

式中：f=33.75u-2.25×108Δx。

式(8)、(9)分别为静态力和动态力模型，阻尼系数C0可由作动器等效质量、刚度系数和空载谐振频率算得。由图2修正前后的静态力模型可知：修正后模型更符合真实压电作动器的输出能力。考虑作动器在隔振中需提供伸缩位移，工作点选择工作曲面中间位置(u=50 V，Δx=7.5 μm，f=0处)。应注意压电作动器的位移输出能力有限，若扰动力幅值超过一定限度，作动器可能会发生位移饱和，导致主动隔振失效。

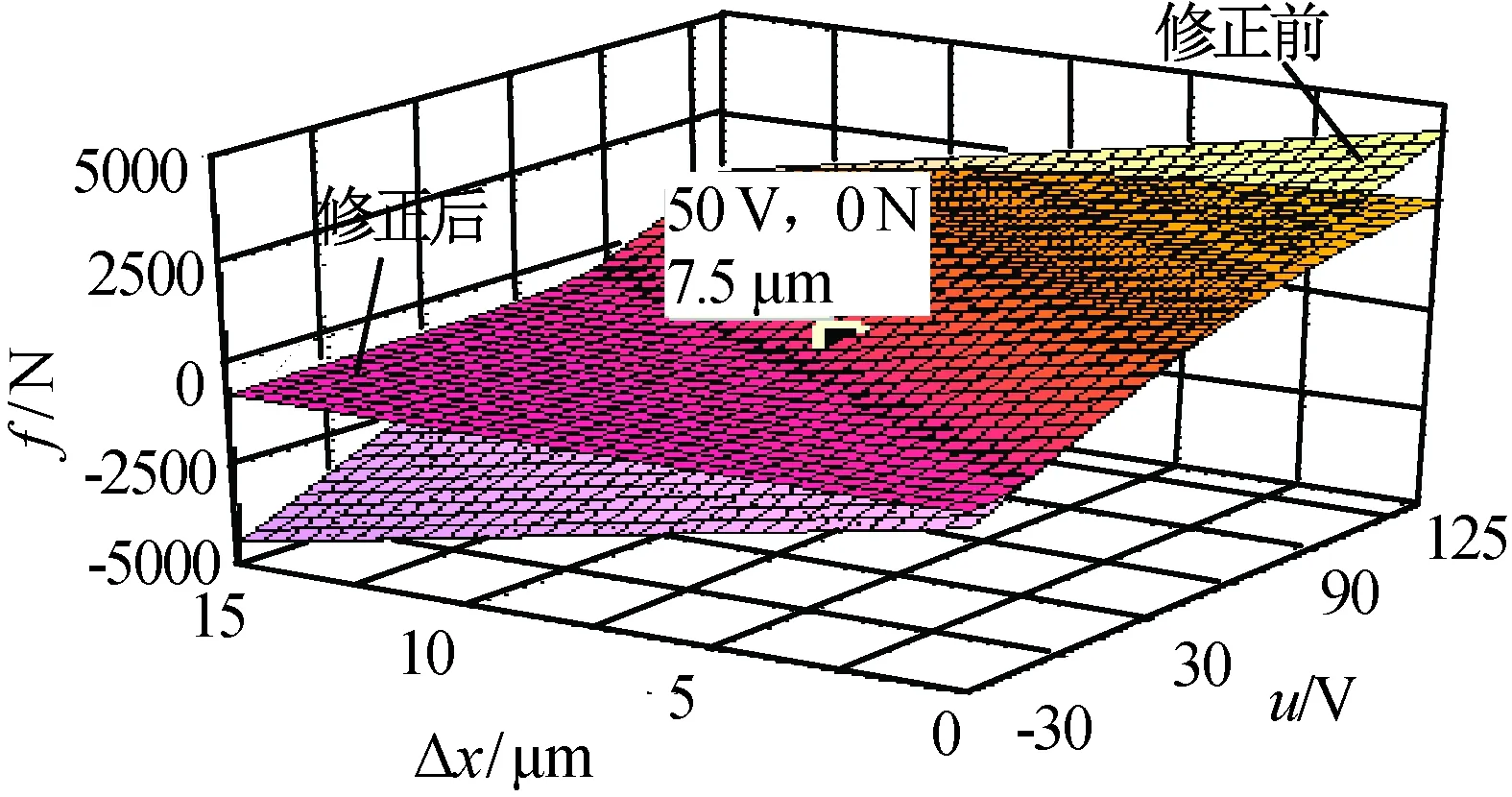
图2 静态力模型修正前后对比Fig.2 Comparison of fsta before and after correction

功放模块内部可视作如图3(a)所示的等效电路，作动器作为容性负载C接入。根据6 μF负载测试数据辨识出一阶传递函数

(10)

式中：Uc为低压控制信号；U为作动器驱动电压。

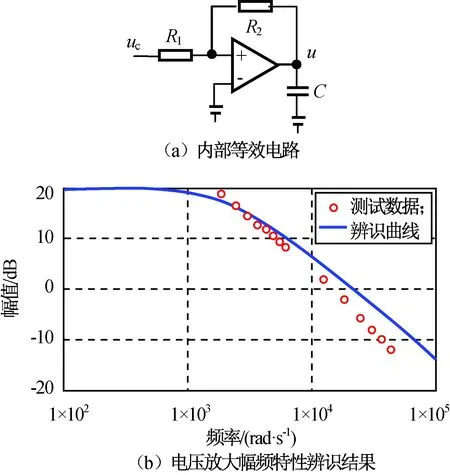
图3 E-505功放模块Fig.3 E-505 amplifier

上述作动器模型忽略了滞环、蠕动和温漂等非线性特征，但由于综合了理论和硬件参数，有助于提高主动隔振控制算法的仿真验证可信度。功放模块建模中选用PI Ceramic配套产品E-505功率放大模块，参数为输入电压-2～12 V；输出电压-30～130 V；电压增益(10±0.1)V；噪声(0～100 kHz)<0.6 mV(rms)[7]。

3 单轴主动隔振

基于以实际产品级压电作动器为参照建立的作动器数学模型，讨论使用该作动器的单轴主动隔振。研究中仿真部分采用修正的作动器模型以保证其可信度，设计控制系统时用式(9)在工作点结果进行线性化，作动器等价于弹簧、阻尼和压控力发生器并联的结构，扰动质量M1和载荷质量M2分别连接到作动器两端，如图4所示。

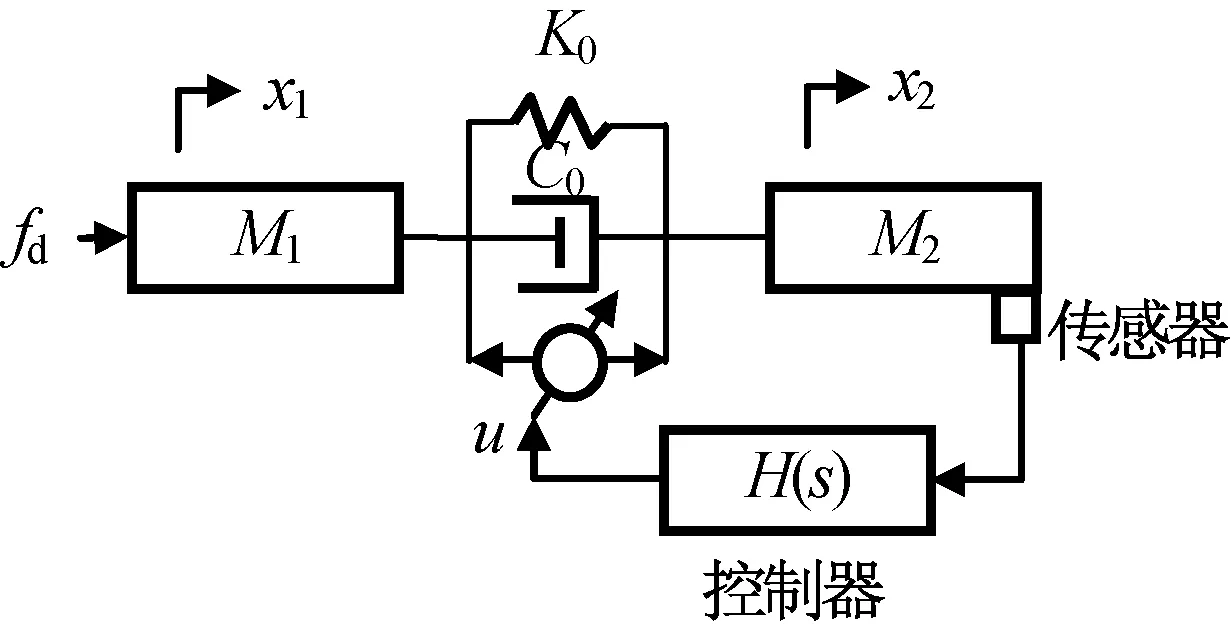
图4 线性化的压电作动器单轴隔振系统Fig.4 Linearization single axis vibration isolation system

建立该系统的状态空间模型

(11)

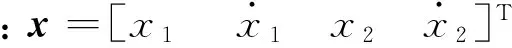
(12)

将式(12)代入(11)，得闭环系统

B1Fd(s).

(13)

式中：I为单位阵。

本文主动隔振采用如下策略：使作动器的运动趋势(速度/输出力)总是与扰动端在截止频率以上的振动分量互补，起到低通的隔振效果，即当扰动端有挤压趋势，作动器收缩避让；当扰动端有拉伸趋势，作动器伸长追随。常规PID算法即可实现该策略，此外可添加高通滤波器调整隔振截止频率和低通特性。

反馈回路H(s)为标量传递函数，由传感器、控制器和功放模块串联而成，有

H(s)=Gamp(s)Gc(s)Gm(s).

(14)

对振动的测量以速度和受力(加速度)为主，两类传感器可用二阶高通滤波器描述为

(15)

式中：Km为传感器增益；ζm为阻尼比；ωn为转折频率。取Km=1，ζm=0.707，ωn由具体传感器决定。当振动频率小于ωm时测量输出迅速衰减，有助于控制器输出自动归零，尽可能避免作动器位移饱和导致隔振失效。

3.1 速度反馈控制

速度反馈中C=[0 0 0 1]，D=0；用检波器测量速度，ωm=12.57 rad/s(2 Hz)；M1=50 kg，M2=2 kg，设计带高通滤波的近似微分PID控制器Gc(s)，速度反馈主动隔振效果如图 5～8所示。

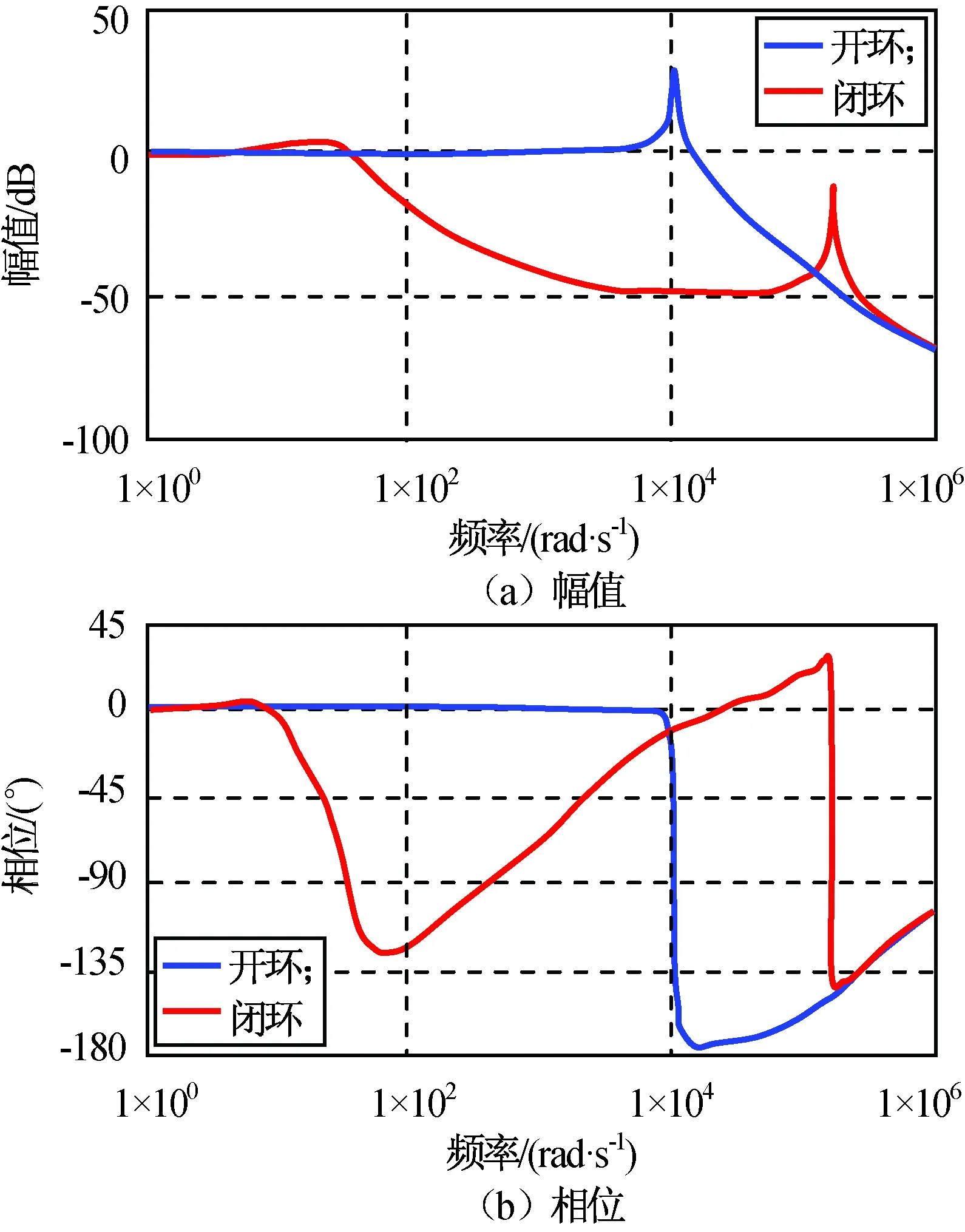
图5 第Ⅰ类隔振性能Bode图Fig.5 Bode diagram of class Ⅰ isolation

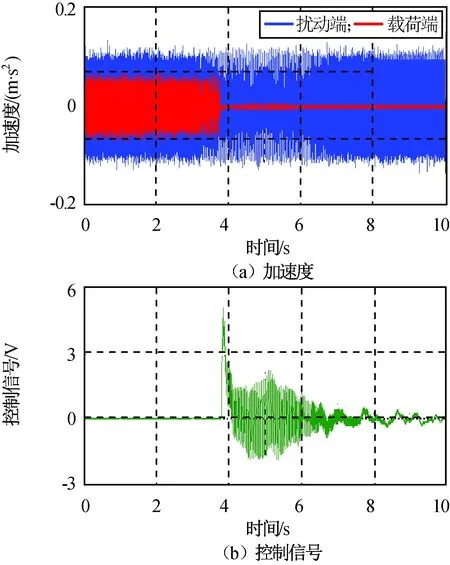
图6 二次变频正弦+零均值高斯噪声扰动Fig.6 Double conversion sine and Gaussian noise disturbance with zero mean value

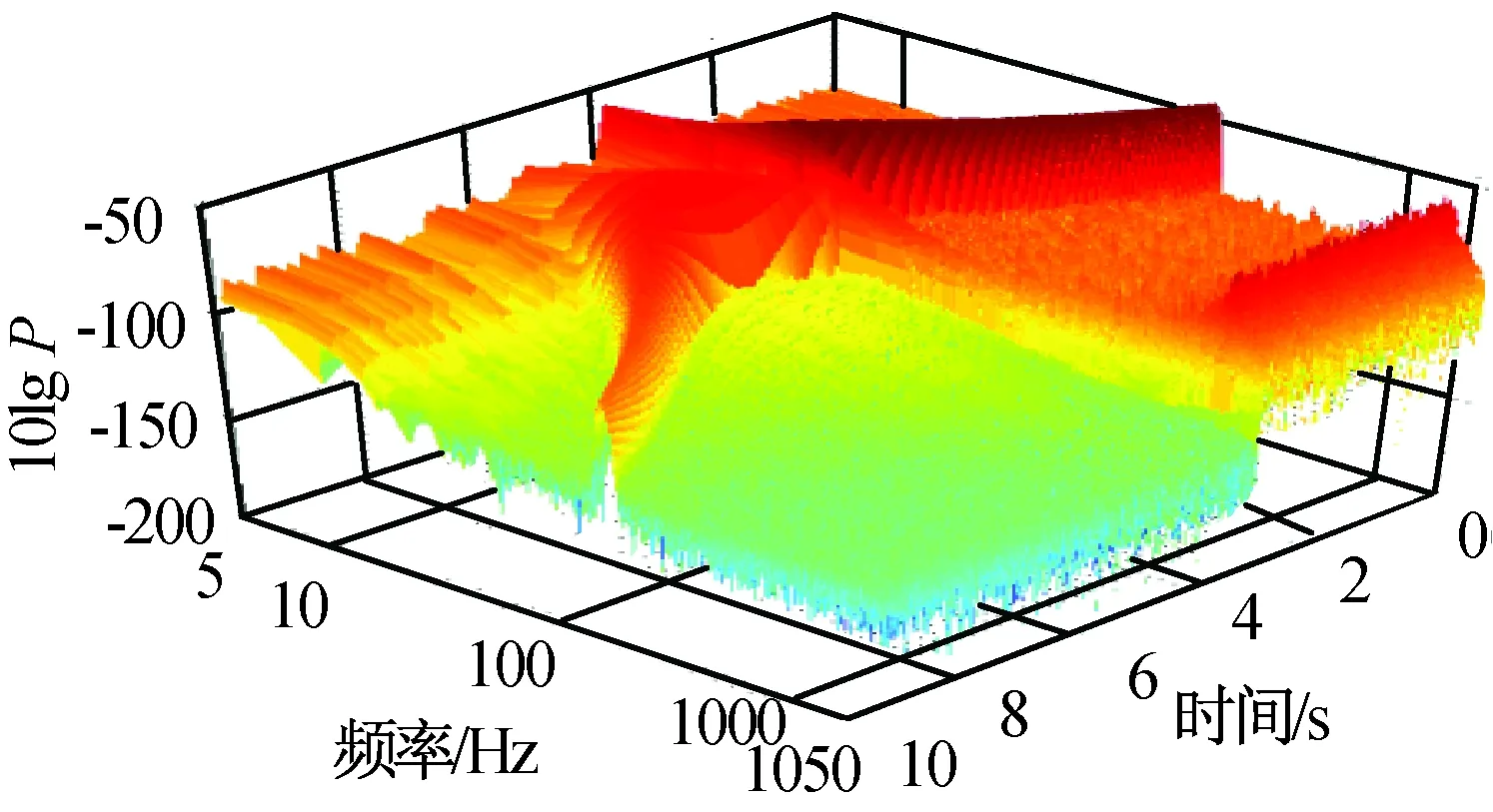
图7 载荷端加速度对数功率谱密度Fig.7 Logarithmic power spectral function of acceleration at load end

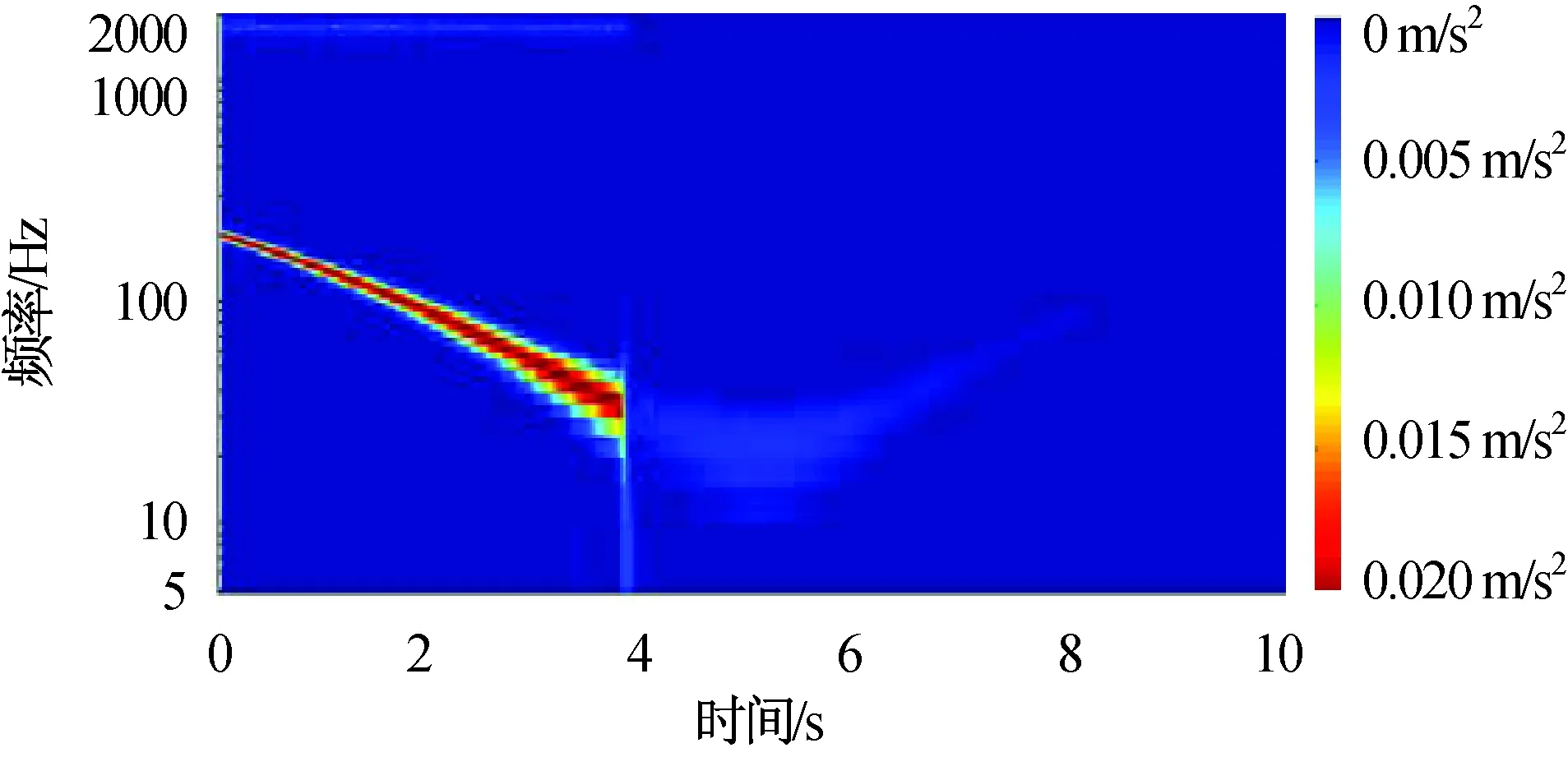
图8 载荷端加速度振幅频谱Fig.8 Amplitude spectrum of acceleration at load end

扰动输入由二次变频正弦和零均值高斯噪声叠加而成：正弦信号幅值2 N，二次变频以5 s处20 Hz为对称轴，0，10 s处200 Hz为端点；零均值高斯噪声σ2=1 N2。主动隔振在约3.7 s时起动，在此之前系统带宽很高，载荷端振动显著，随机扰动在开环谐振频率(约1.6 kHz)处被放大；闭环后中频衰减在-20 dB以上，高频衰减达-50 dB。由图6、7可知：算法能较好应对时变复杂扰动。图5中的高频尖峰是由近似微分控制形成的。此外由图6中控制信号可知：对相同幅值不同频率的扰动，对抗低频扰动所需的作动器位移范围更大，故闭环截止频率附近是易发生位移饱和的频段。

3.2 力反馈控制与代数环引入

空间隔振普遍存在振子质量大、扰动力小的情况，导致加速度、速度的量级很小，力反馈更便于工程实现。测量载荷端受合力作为反馈，则C=[K0C0-K0-C0]，|D|=Kv。

需说明的是，力反馈易引入代数环困难。因D非零，且作动器是输出力的执行机构，故回路中形成了控制信号不经惯性环节(或时间常数极小，<10-6s)直接影响测量信号的通道，类似于数值仿真中的代数环。仿真中可通过减小步长保证收敛，而实际系统采样周期不能无限缩小，可能因代数环导致作动器持续饱和或满幅振荡，即采样频率不足导致发散。用近似微分法设计力反馈的近似比例PD控制器

(16)

式中：kp，ki分别为比例和积分系数；α为近似比例系数；Ghp(s)为高通滤波环节。由上述质量参数，可得不同α的最远闭环极点见表1，第Ⅱ类隔振性能Bode图如图9所示。

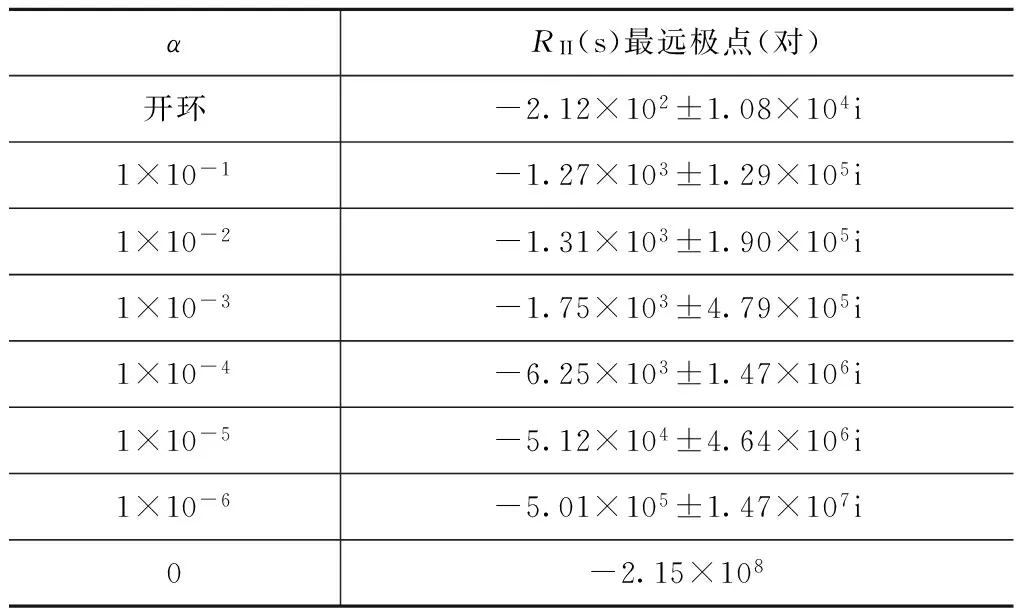
表1 不同α的最远闭环极点

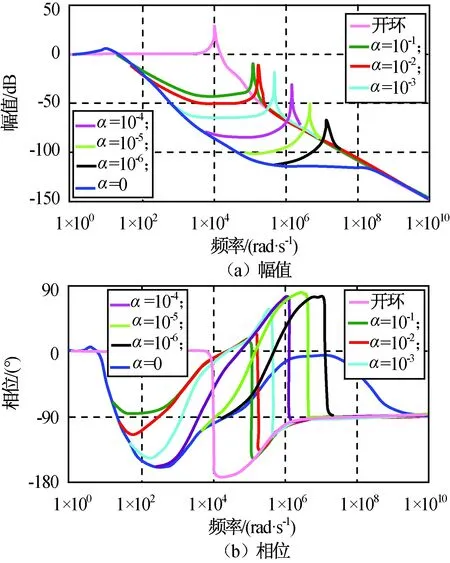
图9 不同α时的第Ⅱ类隔振性能Bode图Fig.9 Bode diagram of performance Ⅱ with different α

上述结果表明：随着α减小至零，虽然隔振能力增强，但闭环极点中的高频极点对迅速远离原点，意味着控制周期须同步减小，即代数环程度逐渐严重。理论上载荷端受力与速度的测量信号只相差1/(M2s)积分环节，故速度反馈中微分控制项也存在类似隐患，可通过近似微分的方式缓解其影响。

3.3 质量对隔振效果的影响

不同于常规地面隔振，空间单轴隔振问题中两端振子无约束，故须考虑扰动端质量M1与载荷端质量M2的大小关系，据此将隔振问题分为三类。

a)大质量扰动端向小质量载荷端的隔振(M1≫M2)，称为正向隔振，如星载激光通信设备对星体振动的隔离。

b)扰动端与载荷端的质量较接近(M1≈M2)，称为不定向隔振，如星载大质量成像设备对星体振动的隔离。

c)小质量扰动端向大质量载荷端的隔振(M1≪M2)，称为反向隔振，如星体对力矩陀螺或飞轮等振动的隔离。

根据上述分类，取μ=M2/M1作为隔振方向因子，μ≪1，μ≈1，μ≫1时分别对应正向、不定向和反向隔振。以力反馈为例，给出闭环特征多项式Δ(s)和第Ⅰ、Ⅱ类隔振性能RI(s)，RII(s)分别为

Δ(s)=s2{[1-KvH(s)]s2+

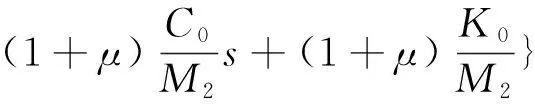
(17)

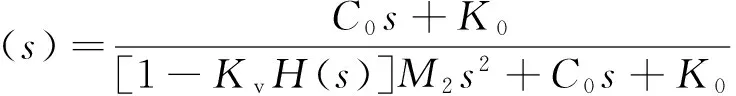
(18)

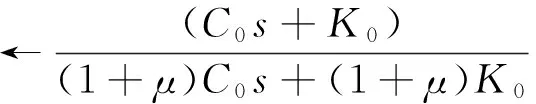
(19)

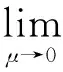
为解释该矛盾，对质量50，2 kg进行正、反向隔振仿真，H(s)保持不变，输入同为幅值0.01 N、频率10 Hz的正弦扰动，所得Ⅰ、Ⅱ类性能Bode图如图10所示，正向隔振Ⅲ类性能如图11所示，反向隔振Ⅲ类性能如图12所示。由图可知：正向隔振中控制切换前后扰动端振动基本不变；反向隔振中振幅剧烈增大，这种负面影响在RⅠ(s)中恰好形成分子变小分母变大效果，造成RⅠ(s)性能提升的误判，故第Ⅰ类隔振衡量标准只适于正向隔振。此外正向隔振中作动器的动作幅度远小于反向隔振，后者甚至出现作动器饱和导致主动隔振短时失效。因此，在作动器行程范围内反向隔振能对抗的扰动幅值范围远小于对应的正向隔振。

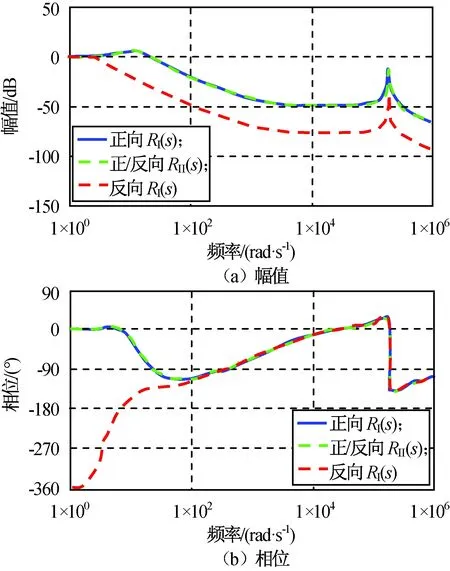
图10 Ⅰ，Ⅱ类性能Bode图Fig.10 Bode diagram of performance Ⅰ and Ⅱ

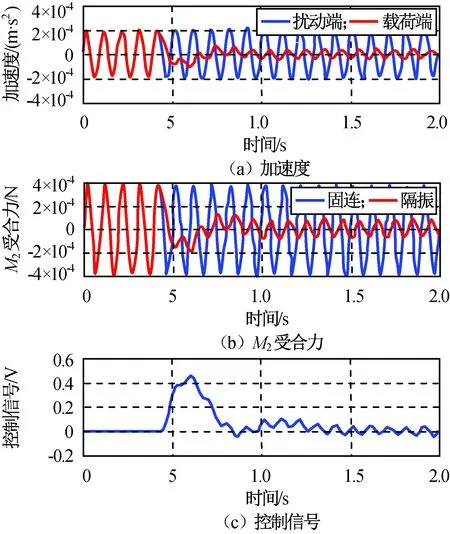
图11 正向隔振Ⅲ类性能Fig.11 Performance Ⅲ of forward vibration isolation

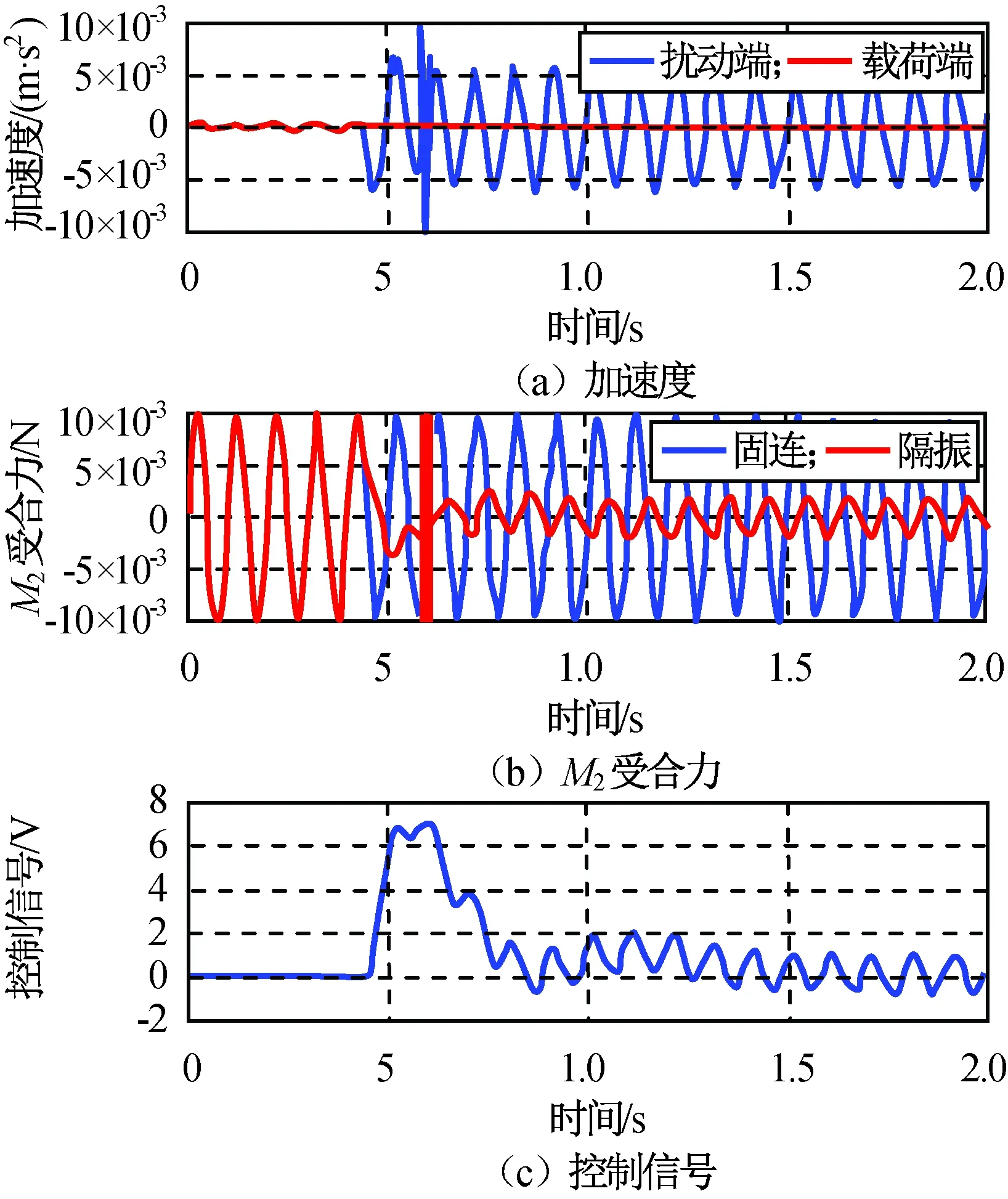
图12 反向隔振Ⅲ类性能Fig.12 Performance Ⅲ of backward vibration isolation

考虑RⅡ(s)也未体现扰动端的激振，计算扰动端受合力在隔振前后的对比。称为隔振或衰减代价，其幅频特性总大于0 dB，正向隔振全频段略高于0 dB；反向隔振在截止频率之上远高于0 dB。有时工程中并不希望这种负面影响，如扰动端有高速转子的姿态执行机构，长期附加振动将影响轴承寿命。在实际应用(特别是反向隔振)中应结合RⅡ(s)，Rc(s)共同衡量隔振性能。

(20)

4 结束语

本文对六自由度空间Stewart隔振平台中单轴主动隔振进行了研究，提出了三类隔振衡量标准，建立压电作动器数值修正模型，设计主动隔振策略并以速度和力反馈分别实现。提出了隔振方向和隔振代价的概念，为后续设计六自由度空间Stewart隔振平台提供了理论参考。

[1] BAZ A, POH S. Performance of an active control system with piezoelectric actuators[J]. Journal of Sound and Vibration, 1988, 126(2): 327-343.

[2] ANDERSON E H, FUMO J P, ERWIN R S. Satellite ultraquiet isolation technology experiment (SUITE)[C]// Aerospace Conference Proceedings. [S. l.]: IEEE, 2000(4): 299-313.

[3] 李国平. 基于精密仪器设备的主动隔振关键技术研究[D]. 杭州: 浙江大学, 2010.

[4] 张伟， 赵艳彬， 廖鹤， 等. 动静隔离、主从协同控制双超卫星平台设计[J]. 上海航天， 2014， 31(5)： 7-11.

[5] HAUGE G S, CAMPBELL M E. Sensors and control of a space-based six-axis vibration isolation system[J]. Journal of Sound and Vibration, 2004, 269(2): 913-931.

[6] KIM S, PIETRZKO S. Active vibration isolation using an electrical damper or an electrical dynamic absorber[J]. IEEE Transactions on Control Systems and Technology, 2008, 16(2): 245-254.

[7] HANICH A A. Active isolation and damping of vibrations vie stewart platform[D]. Bruxells: University of Libre de Bruxelles, 2003.

[8] Physik Instrumente. Piezoelectric actuators[EB/OL]. [2014-6-15]. http: www.piceramic.de.

Spaceborne Single Axis Active Vibration Isolation Based on Piezoelectric Actuator

QIU Wei1, ZHU Qing-hua2, 3, LI Jie-dong2, 3, SHI Gui-guo2, 3

(1.College of Control Science and Engineering, Zhejiang University, Hangzhou 310027, Zhejiang, China; 2. Shanghai Key Laboratory of Aerospace Intelligent Control Technology, Shanghai 201109, China；3. Shanghai Institute of Spaceflight Control Technology, Shanghai 201109, China)

The single axis active vibration isolation on the spaceborn Stewart vibration isolation platform with six degree of freedom was studied based on piezoelectric actuator in this paper. Three kinds of measurement standards were put to evaluate isolation performance. Among those, the first one was ratio of vibration quantities at the payload end to disturbance end with the same dimension, and the second one was ratio of force at the payload end after isolation to force while being mounted before isolation, as well as the third one was attenuation of vibration quantity before and after isolation. The general equation of piezoelectric actuator was given and was modified according to the real situation. The linearization single axis vibration isolation system based on piezoelectric actuator was established. The active vibration isolation strategy was adopted in which the actuator motion was always matched the vibration at disturbance end. The velocity feedback control, force feedback control and algebraic loop leading in, and effects of mass on the isolation performance were discussed. The concept of reduction direction and reduction cost were put forward. The simulation results showed that good isolation performance would be obtained through velocity feedback and force feedback. The influence of reduction direction on both reduction performance and reduction cost was analyzed theoretically. The study provides some reference for designing spaceborne Stewart vibration isolation platform.

Spaceborne Stewart vibration isolation platform with six degree of freedom; Single axis active vibration isolation; Piezoelectric actuator; Isolation performance; Measurement standard; Velocity feedback control; Force feedback control; Reduction direction; Reduction cost

1006-1630(2016)05-0029-07

2015-08-20；

2015-12-20

邱 炜(1990—)，男，硕士，主要研究方向为航天器姿态及轨道控制。

V414.33

A

10.19328/j.cnki.1006-1630.2016.05.005