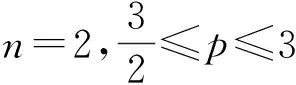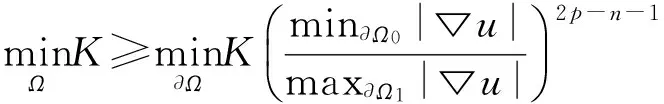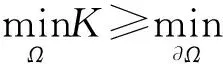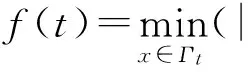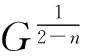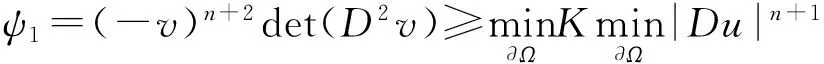椭圆与抛物偏微分方程解的凸性
麻希南
(中国科学技术大学数学学院,合肥230026)
椭圆与抛物偏微分方程解的凸性
麻希南
(中国科学技术大学数学学院,合肥230026)
我们给出椭圆与抛物偏微分方程解或其水平集的凸性的一个文献综述.从三个经典例子开始,然后介绍凸性研究的常用方法,最后给出几个定量估计,其中注重与我个人研究有关的结果.
偏微分方程解的凸性; 偏微分方程解的水平集的凸性; 常秩定理; 凸性定量估计
1 凸性的研究历史:三个经典例子
长久以来偏微分方程解的几何性态是偏微分方程研究的重要课题之一,椭圆与抛物偏微分方程解或其水平集的凸性是重要的研究对象.凸性除了本身具有几何意义之外,它与方程解的正则性、存在性以及唯一性都有紧密的联系.我们从有关的三个例子开始谈起.
例1 凸区域上Green函数的水平集的凸性.
Caratheodory[2]于1920年代给出了二维凸区域的Green函数的水平集的凸性.在1931年,Gergen[29]证明了三维欧氏空间中星形区域的Green函数的水平集也是星形的.1956年,Shiffman[76]给出了有关水平集凸性的第一个明确的结果.对于3中两条曲线所界定的参数极小曲面,当该两条边界曲线分别是两平行平面上的凸曲线时,Shiffman用复分析的方法证明了中间平行平面与极小曲面的截线是严格凸的,进而还可知该极小曲面是嵌入的.Shiffman的结论对极小曲面的研究有重要的意义,后来亦导致了相应的Douglas-Plateau问题的完全解决.
1957年,Gabriel[28]首先证明三维欧氏空间有界凸区域上Green函数的水平集是严格凸的.1977年,Lewis[58]推广Gabriel的定理到高维p-调和函数并得到以下定理
定理1.1(Gabriel[28]和Lewis[58]) 令u满足
(1.0.1)
这里1 其思想方法是引时如下的“凹性函数”: 显然,u的水平集是凸的充要条件是Q(x,y)≥0,∀(x,y)∈Ω×Ω.在证明水平集严格凸性时他们利用调和函数的实解析性.我们为了说明常秩定理的应用方法,在第四章给出Korevaar[55]的关于调和函数时此定理的新证明. 例2 Makar-Limanov[65]在1971年研究了如下边值问题: (1.0.2) 例3 1976年,Brascarmp-Lieb[12],他们通过研究热方程 (1.0.3) 其中Ω为有界凸区域,u0是边界上为零的给定正函数.当logu0是凹函数时,他们证明了t>0,logu也是凹的(关于x).而且得到了欧氏空间中凸有界区域上的第一特征函数 (1.0.4) 的对数logu是凹函数.从而也得到了第一特征值的关于区域的Brunn-Minkowski不等式,在[23]Colesanti得到Brunn-Minkowski不等式中的等号成立当且仅当两个凸区域是同位相似(homothetic). 后面两个例子说明有时候偏微分方程的解本身不一定是凸的,但关于解的某个函数可能具有某种凸性(从而解的水平集也是凸的).以上是有关凸性研究的一些经典事例,由此可以看到,偏微分方程解的凸性研究长久以来一直是人们所关心的重要话题. 2.1 椭圆方程解的凸性的宏观方法:比较原理和凹包络 当某个偏微分方程的解本身是凸的时候,它的水平集自然是凸的,所以,证明偏微分方程的解凸性的方法也可以看作是证明水平集凸性的一种(间接)方法,这些思想方法之间是相互影响相互借鉴的.与Gabriel的凹性函数Q(x,y)相对应,1983年Korevaar[53]在研究毛细管曲面方程的解的凸性时引进如下凹性函数 φ(x,y,λ)=u(z)-λu(x)-(1-λ)u(y), 其中z=λx+(1-λ)y, 0≤λ≤1, ∀x,y∈Ω.我们可以看出u为凸函数当且仅当在Ω×Ω中φ(x,y,λ)≤0. Korevaar[54]对一类半线性椭圆方程的解推出了关于上述凹性函数极值原理,由此得到解的凸性,他给出了Brascamp-Lied[12] 的欧氏空间中凸有界区域上的第一特征函数对数logu凹性的新证明,Caffarelli和Spruck[17]同时用类似的想法也给出它的新证明.最近两点辅助函数被Andrews[4]用来给出平均曲率流中Sheng-Wang[74]Non Collapsing估计的新证明与Brendle[13]的子流行中有名的Lawson猜想证明. Korevaar的凹性极值原理后来得到Kennington[51],Kawohl[50]和Greco Porru[30]等人的许多推广和发展(可见Kawohl[49]及其参考文献).Korevaar的凹性极值原理实际上是一种弱极值原理或比较定理,我们按Korevaar[55]称它是凸性研究的宏观方法.宏观方法的进一步发展是Alvarez-Lasry-Lions[3],他们用凹包络的方法证明了一类完全非线性椭圆方程在凸区域具有边界限制下解的凸性.对于由Korevaar和Alvarez-Lasry-Lions等人推广的凹性极值原理和凹包络这种宏观的方法,应用起来有很多限制.例如它常常只能处理有界凸域(凸环)的情形,在无边情形或者流形上使用受到限制.另外,用宏观的方法往往很难得到严格凸性或刚性,而严格凸性或刚性通常在解决几何问题时经常是起关键作用的. 2.2 椭圆方程凸解的微观方法:常秩定理 除了上述宏观的方法,也有利用强极值原理来研究偏分方程解的凸性,按Korevaar[55]我们称它是微观方法.它是利用强极值原理加上形变的思想或也称连续性方法,并且已发展出一个强有力的工具——常秩定理.最早的文献是Caffarelli-Friedman[14](也可见Singer-Wong-Yau-Yau[77]).常秩定理是用连续性方法来证明凸性问题的一个关键步骤.我们用第一章的例2来说明它的应用过程.对以下方程 (2.2.1) (2.2.2) 首先Caffarelli-Friedman[14]证明,对于任意区域Ω如果方程(2.2.2)的解v是凸函数,那么它的Hessian矩阵的秩在整个区域中是常数.然后他们在区域是球B1(o)⊂2时证明相应方程的解v是严格凸的(秩为二),令Ωt=tΩ+(1-t)B1(o),再将区域由球连续形变到凸区域Ω.若在形变过程中的某个时刻0 二维情形的常秩定理首先被Caffarelli-Friedman[14]得到,并成功应用到解决2维凸区域上几类半线性椭圆方程解的严格凸性和刚性问题.后来,Korevaar Lewis[56]把常秩定理推广到高维情形,特别是应用常秩定理,他们重新得到了方程(2.2.2)高维结果,并很算然地给出了严格凸性. 近年来,常秩定理陆续被应用到来源于经典微分几何里的Christoffel Minkowski问题(Guan-Ma[34],也见Hu-Ma-Shen[41])和预定Weingarten曲率问题所导致的完全非线性偏微分方程(Guan-Lin-Ma[32,33]和Guan-Ma-Zhou[35]).例如Guan-Ma[34]将常秩定理推广到非线性椭圆方σk(uij+uδij)=f(x),x∈Sn(这里σk(uij+uδij)是球Hessian矩阵(uij+uδij)特征根的第k-阶基本对称多项式),这里f(x)满足一定的凸性条件.后来Caffarelli-Guan-Ma[15]把相应的结论推广到一类完全非线性椭圆方程 F(D2u)=f(x,u,Du), 这里F,f满足某种凸性的结构条件.Bian-Guan[6]把常秩定理推广到更一般的一类完全非线性椭圆方程 F(x,u,Du,D2u)=0, 它要求函数F(x,u,Du,D2u)满足某种凸性的结构条件,可是在实际问题中往往很难去验证此类结构条件.在Ma-Xu[68]和Liu-Ma-Xu[59]中,为了推广例2与例3到高阶σk(D2u)方程的对应问题,他们研究一类三维凸区域上一类σ2(D2u)方程的解的凸性以及对应的常秩定理.他们得到凸区域上一类非线性算子的特征值的Brunn-Minkowski不等式,并刻画了等号成立时当且仅当两区域相差一平移和伸缩,是本领域中少有的典型的例子.最近Salani[72]给了凸性的新证明,但还是有3维的限制. Han-Ma-Wu[38]研究以下问题:Poisson方程的解的Hessian矩阵的最小k个特征值之和何时是正的?其中k=1时即为Caffarelli-Friedman[14]和Korevaar-Lewis[56],他们利用常秩定理得到一个充分条件,问题的困难是它所对应的矩阵很大,它最后归结为一个关于方程解的3阶导数的有关量的一个组合问题.我们提到其它应用如Wang-Xia[79]在利用几何流去证明双曲空间中等周不等式中时用到了常秩定理保住严格凸性,Guan-Li-Zhang[31]在Kahler几何中应用了常秩定理得到刚性问题. 2.3 抛物方程解的空间凸性与时空联合凸性 首先我们关心研究抛物方程解凸性的概率方法. Brascamp-Lieb[12]利用Brownian运动中的Feymann—Kac公式研究了抛物方程的解对于空间变量的凸性,他们证明如果初值满足logu0是凹函数时,则对∀t>0,logu关于空间变量x也是凹的.对于Brownian运动的技术在抛物方程凸性的应用,Borell[9-11]有各种情形的推广,例如Borell对于具Schrödinger位势的抛物方程,他研究其解的时空凸性从而给出Brascamp-Lieb[12]定理的新证明以及Brunn-Minkowski不等式的Brownian运动证明.他的论文对抛物方程解或水平集的时空联合凸性有重要影响. 抛物方程解凸性的宏观方法. Korevaar[54]和Kennington[52]也有相应两点辅助函数的凹性函数极值原理在空间凸性与时空联合凸性的推广与应用.相关凹包络的技巧在抛物偏微分方程关于研究解得空间凸性与时间联合凸性的推广见Ishige-Salani[45]与[46],以及Ishige-Nakagawa-Salani[47]在抛物偏微分方程组的时空联合凸性以及在对应椭圆方程组的应用.但是在Ishige-Salani[45]的工作中他们往往要求抛物偏微分方程的初值条件是零函数,这是一个很大的限制. 抛物方程解凸性的微观方法. 在论文[6,15]中,他们研究了非线性抛物方程解的Hessian矩阵对于空间变量的常秩性质,[6]也研究超曲面几何流的保住凸性.受Borell[10]的启发,Hu-Ma[39]对一类抛物偏微分方程其凸解的时空Hessian矩阵的常秩性,并且证明Borell[10]中的时空凸解具有常秩性.然后Chen-Hu[20]他们简化了[39]中的计算,对于一类完全非线性抛物方程得到其凸解的时空Hewssian矩阵的常秩性.这类技巧在抛物方程水平集凸性的研究中有重要应用. 2.4 凸性研究的其它方法与技巧以及应用 3.1 椭圆方程解水平集凸性研究的宏观方法:凹性极值原理和凹包络 我们在凸性的研究历史中已经知道Gabriel[28]和Lewis[58]研究了凸区域的Green函数的水平集的凸性.Caffarelli-Spruck[17]推广Gabriel的方法得到凸环上半线性椭圆方程 解的水平集为凸的.其中Ω0以及Ω1是n中的凸区域,且满足1⊂Ω0,f(0)=0,f(t)是非负单调递增函数.事实上,利用定理条件可证明解在凸环上满足|▽u|>0. 将u延拓,使得在Ω1在u=1.然后定义凹性函数 在2003年,Colesanti-Salani[24]利用拟凹包络研究了凸环上拟线性方程在一定结构条件下水平集的凸性.最近Bianchini-Longinetti-Salani[8]中用拟凹包络的办法证明了凸环上完全非线性方程在一定结构条件下水平集的凸性. 先描述一下函数u的拟凹(Quasiconcave)包络的概念.函数u为上半连续函数,用u*表示u的拟凹包络,粗略地说,拟凹包络u*是其上水平集为u的上水平集的闭凸包的上半连续函数.具体地说,记Ω(t)为u在t处的上水平集,即 Ω(t)={x∈n|u(x)≥t} 用Ω*(t)表示其凸包的闭包.u*可以定义为 Ω*(t)=sup{t∈|x∈Ω(t)} 由于u*为比u大的最小的上半连续拟凹函数,从而有u*≥u.只要证明反过来的不等式成立,利用u*的拟凹性,则知道水平集为凸的.从而,若假设u是椭圆方程的下解,且方程满足比较原理,此时即有相反的不等式成立.具体地说,[8]证明了下面的定理: 设Ωt0和Ωt1为n中的有界开子集,满足t1⊂Ωt0,记凸环.设为下列Dirichlet问题的经典允容许解, 其中t0 (i) |Du|≠0于Ω; (ii)F(x,t,p,A)关于t单调递减; (iii)F(x,t,p,A)是退化椭圆的,即F(x,t,p,A)≤F(x,t,p,B),对任意地称矩阵A,B,且A-B为正定矩阵; (iv) 存在α∈,对任意的(t,θ)∈(t0,t1)×Sn-1,函数在Ωt0×(0,+∞)×ΓF(这里ΓF为对称矩阵)上为凹函数. 则拟凹包络u*为该Dirchlet问题的粘性下解.Longinetti-Salani[63]中利用支撑函数建立了一组拟凹函数水平集曲率的关系式对该定理的证明起了关键作用. 3.2 椭圆方程解水平集凸性研究的微观方法:常秩定理 类似于研究解本身的凸性,也可从微观角度应用常秩定理研究水平集的凸性.受Caffarelli-Friedman[14]和Korevaar-Lewis[56]的启发,Korevaar[55]建立了p-调和函数的凸水平集的第二基本形式的常秩定理,然后利用形变过程加上先验估计就得到了Gabriel[28]和Lewis[58]定理的新证明.我们在凸环上调和函数水平集的严格凸性将给出Korevaar[55]关于调和函数的证明(也见[7]).他对于平均曲率方程也有相应的常秩定理,所以他得到对于凸环上具有齐次Dirichlet边界条件的极小图,则其水平集是严格凸的.Xu[83]推广Korevaar[55]的常秩定理到一类线性椭圆方程.我们已经知道Bianchini-Longinetti-Salani[8]中用拟凹包络的办法证明了凸环完全非线性椭圆方程在一定结构条件下水平集的凸性,对应于此类方程的常秩定理,Bian-Guan-Ma-Xu[7]和Guan-Xu[36]证明[8]的凸水平集是严格凸的.前面我们巳经提到Shiffman[76]的参数极小曲面在一定条件下其水平集的严格凸性,为了得到其高维参数极小曲面对应的推广,Hu-Ma-Ou[40]给出了n中预定平均曲率的浸入超曲面凸水平集第二基本形式的常秩定理,但是对应的形变过程至目前没有找到. 3.3 抛物方程解的水平集研究的宏观与微观方法 我们研究抛物方程的类似问题,即如何在给定初始条件,边值和区域的几何条件下,我们有对解的更好的几何认识.例如人们期望在一定条件下能够得到对任意给定时间,解对空间变量的凸性或水平集的凸性.或是否具有某种对于时间变量和空间变量的联合凸性.我们已经知道Bracamp-Lieb对于热方程,在凸区域并齐次边界Dirichlet条件,他们证明如果初值函数的对数为凹函数,那么对任意时间,解的对数函数对空间变量是凹的.我们先给出几个定义.我们回忆函数v:m→∪{-∞}在m(m∈)为拟凹或水平集是凸的(quasiconcave),如果它的所有上水平集{y∈m∶v(y)≥c}是凸的.如果v只在真子集A⊂m上有定义,我们在A外令它等于-∞,我们称v在A中是拟凹的如果在m这种延拓在m上是拟凹的. u((1-λ)x0+λx1,t)≥min{u(x0,t),u(x1,t)}, (3.3.1) 对∀x0,x1∈Ω0,λ∈(0,1)以及所有固定的t≥0. 类似的,u是时空拟凹(spatially-time quasiconcave)如果 u((1-λ)x0+λx1,(1-λ)t0+λt1)≥min{u(x0,t0),u(x1,t1)}, (3.3.2) 显然,如果函数是时空拟凹(或时空水平集凸,spatially-time quasiconcave),则对于每一个因定的时间它是空间拟凹的. 在1982年,Borell[9]利用Brownian运动的Feymann-Kac公式和Gabriel[28]与Lewis[58]技巧的抛物对应,考虑了在凸环上给定常数边值的初边值问题.他得到如果初值是零函数,则热方程解的水平集是时空联合凸,即他研究 (3.3.3) 对于以下初边值问题 (3.3.4) 他得到以下定理 在2010和2011,Ishige-Salani[43,44]给出了上述Borell定理的一个新证明,他们推广到一类完全非线性抛物方程,并且他们引进抛物拟凹的概念.他们有一个很强的条件即初值必须为零函数.但是Ishige-Salani[42]在2008年的给出例子说明,即使对于热方程如果初始值的水平集是凸的,则不能保证得到解对空间变量的水平集的凸性.所以自然的问题使我们要对初值加何种几何分析条件,使得具有解对空间变量水平集的凸性?在Chen-Ma-Salani[21]中我们得到以下结果. (3.3.5) 注3.4 上面定理的初值条件u0出现的Diaz-Kawohl([26]和[27])中,并且初值u0(x)满足所需条件的存在性是知道的(如可以取Δu0≡1 inΩ,可以见[8]).从[27]知道,初值(3.3.5)保证 ut>0, |Δu|>0 inΩ×(0,+∞). (3.3.6) 它对于我们定理的证明是关键的. 我们通过一个形变过程加上以下的热方程解的时空凸水平集第二基本形式的常秩定理证明以上定理.现在我们叙述热方程解的时空凸水平集第二基本形式的常秩定理. 上面常秩定理的证明非常复杂,因为我们需要对于抛物方程建立时空凸水平集第二基本形式的常秩定理,此时我们利用[39]以及Chen-Hu[20]的简化计算并推广到时空水平集.我们为了说明常秩定理的应用方法,我们在下一节来详细给出Korevaar[55]的关于调和函数的Gabriel[28]和Lewis[58]定理的新证明. 3.4 椭圆方程解的水平集凸性的几个反例 偏微分方程解的水平集的凸性是非常敏感的一个问题,除了我们前面的正面结果,我们叙述最近的两个反例.一个是Wang[82]关于常平均曲率方程的反例,另一个是Hamel-Nadirashvili-Sire[37]对于半线性椭圆方程的反例. 汪徐家关于常平均曲率方程的反例. 很长一段时间以来人们对例2的平均曲率方程的推广是否成立很感兴趣.问题可以叙述如下.令Ω为n(n≥2)中具有光滑边界∂Ω的有界凸区域.H是给定的正常数,如果u为下常平均曲率方程的解,问题是u的水平集是否为凸? (3.4.7) 汪徐家[82]通过rescaling技巧,找到了一类凸区域使得解在边界附近的地方水平集有曲率非正点. Hamel--Nadirashvili-Sire[37]关于半线性随圆方程的反例. 在我们凸性的研究历史的三个例子都是特别简单的方程,稍微一般的具有正面的例子是Caffarelli-Spruck[17]得到的特殊半线性方程.[37]中他们对于一类特别的有界凸区域Ω与一般的方程 他们得到了上水平集非凸的解.类似地他们[37]找到凸环上一类半线性椭圆方程 解的上水平集为非凸的. 我们为了说明常秩定理的应用方法,我们现在来详细给出Korevaar[55]的关于调和函数的Gabriel[28]和Lewis[58]定理的新证明. 4.1 函数u(x)水平集的曲率矩阵 在这一节,我们首先给出水平集凸性的简要定义,然后推出函数的水平集曲率矩阵(aij).该矩阵在([16]和[7])的文章中出现,其特征值即是函数水平集的主曲率. 现在给出函数u的水平集的定义.设Ω为n的区域,并且u∈C2,α(Ω),0<α<1,其水平集通常按下面的方式定义为: 定义4.1 假设在Ω上,u的梯度|Du|≠0,则u通过x0∈的水平集记为Σu(x0)∶={x∈|u(x)=u(x0)}. 以后在满足|Du(x0)|≠0的点x0处进行计算.在此特殊情形下描述水平集Σu(x0)的凸性.不失一般性,假设un(x0)≠0并且在x0附近的小邻域内进行计算,利用隐函数定理,水平集Σu(x0)局部地可以表示为xn=v(x′),x′=(x1,x2,…,xn-1)∈n-1的图.对函数u(x1,…,xn-1,xn)∈C2(Ω),存在函数v(x′)满足方程 u(x1,x2,…,xn-1,v(x1,x2,…,xn-1))=u(x). (4.1.1) 下面把曲率矩阵(aij)用函数u的导数来表示,计算在Σu(x0)∶={x∈Ω|u(x)=u(x0)}的局部上进行并且假设un(x0)≠0.对称曲率矩阵{aij}为 (4.1.2) 以下引入记号 (4.1.3) 以及 Aij∶=-hij+Bij-Cij. (4.1.4) 此时u的水平集的对称曲率矩阵可写成 (4.1.5) 我们要用到一个引理 引理4.4[6,21]设对于x∈Ω⊂n,有W(x)=(Wij(x))≥0并且Wij(x)∈C1,1(Ω).则对于O⊂⊂Ω,存在一个正常数C,只依赖Hausdorff距离dist{O,∂Ω}和‖W‖C1,1(Ω),使得 (4.1.6) 对于∀x∈Ω以及1≤i,j≤n. 4.2 调和函数u(x)凸水平集的常秩定理 我们考虑方程 (4.2.7) |▽u(x)|=un(x)>0 和 {uij}1≤i,j≤n-1在点x点对角. (4.2.8) 不失一般性我们假设u11≤u22≤…≤un-1 n-1.因此在x∈O,由(4.1.5),矩阵{aij}是对角并且a11≥a22≥…≥all>C.则G={1,…,l}和B={l+1,…,n-1}(“好”和“坏”的指标集).我们也假设 G={a11,…,all},B={al+1 l+1,…,an-1 n-1}. (4.2.9) 令 φ(x)=σl+1(aij). (4.2.10) 利用[14]和[56]的术语,如果h和g为O中的两个连续函数,我们记hg,如果存在两个正常数C1和C2它们只依赖于‖u‖C4,n(独立于x),使得(h-g)(x)≤(C1φ+C2|▽φ|)(x), ∀x∈O.我们也记h~g如果hg和gh. 对于x∈O,在(4.2.8)我们选取坐标系使得|▽u|=un>0并且矩阵{aij(x)}对角非负.从φ的定义,我们有 所以 aii~0, ∀i∈B. (4.2.11) 以及 故 hii~0,uii~0, ∀i∈B. (4.2.12) 对φ求一阶导数 从而 (4.2.13) 故 (4.2.14) 对φ求二阶导,从(4.2.11)和(4.2.13)得到 (4.2.15) 这里我们已经用下列不等式(见引理4.4): 因为uk=0,k=1,…,n-1, 从(4.1.5) 和 故有 这里 对i∈G,j∈B,得到 所以 (4.2.16) 利用 φ(x)≥0,x∈O,φ(x0)=0, (4.2.17) 由强极值原理我们有 φ(x)=σl+1(aij)≡0,x∈O. (4.2.18) 由解的连续性得到a(x)在Ω达到极小秩l之点集的闭性,从而定理4.5成立. 4.3u(x)水平集的严格凸性 Ω0,t=(1-t)BR(0)+tΩ0, (4.3.19) Ω1,t=(1-t)Br(0)+tΩ1, (4.3.20) (4.3.21) 这里求和是Minkowski向量和.故对于0≤t<1,Ωt是一族C2严格凸环(见Schneider[73]).我们记ut为下Dirichlet边值问题得解 (4.3.22) 前面陈述的结论是凸性的定性研究,现在我们关心的问题是我们是否能通过区域的定量信息来得知区域内方程解的凸性或水平集凸性的定量估计.下面我们对凸性的研究历史的三个例子给出用边界数据表示的凸性的定量估计. 例1的相关估计. 由Gabriel[28]和Lewis[58]的定理知道凸环上的满足齐次Dirichlet边界条件p-调和函数的所有水平集是严格凸的.Longinetti[60]和Ortel-Schneider[71]首先证明二维调和函数凸水平集的曲率在边界达到最小值.如果u是在区域上没有临界点的二维调和函数,令k为u的水平集的曲率,Talenti[78]证明|▽u|-1k是一个调和函数.从此可以得到二维调和函数凸水平集曲率的用边界数据给出的上界估计.Longinetti[61]得到极小曲面的类似估计,其水平集的凸性来自于Shiffman[76].Jost-Ma-Ou[48]证明三维调和函数的凸水平集的高斯曲率在边界达到极小.Ma-Ou-Zhang[66]通过高斯曲率首次完整地对任意维凸环上的p-调和函数的凸水平集的高斯曲率给出了一个最佳下界估计,它依赖于区域边界的高斯曲率与p-调和函数的边界梯度估计的上下界.由这些定量估计结合形变过程,可以得到水平集的严格凸性.Ma-Zhang[69]还得到了高维调和函数凸水平集的高斯曲率的沿函数高度的精细的变化关系. 现在叙述我们的估计. 定理5.1[66]令Ω为n,n≥2中的有界光滑区域,为Ω中的p-调和函数,即 div(|▽u|p-2▽u)=0 inΩ. (5.0.1) 情形1 对n≥2,1 |▽u|n+1-2pK 在边界达到极小. |▽u|1-pK 在边界达到极小. 如果u是方程(3.3.1)的解,则容易知道|▽u|在边界达到极大与极小,从而我们有以下推论. 推论5.2 令u满足 (5.0.2) 这里1 (5.0.3) (5.0.4) (5.0.5) (5.0.6) 推广Longinetti[61],[62]利用凸体支撑函数的想法,在Ma-Zhang[69]中他们利用严格凸水平集的支撑函数和最大值原理,他们得到了高维p调和函数凸水平集的高斯曲率的沿函数高度的精细的变化关系.见下面定理 定理5.3[69]令u满足 这里1 Γt={x∈Ω|u(x)=t} for 0 这里K为水平集的高斯曲率.则函数 是t∈(0,1)的凸函数. 下面是一个推论. 推论5.4 在定理5.3的同样条件下,对于∀x∈Γt,0 (i) 对p=2,有 例2的相关估计. (5.0.7) Ma-Shi-Ye在[67]中利用Makar-Limanov[65]的想法,对方程(1.0.2)和(5.0.7)也找到他们辅助函数的高维版本,证明它们的最小值在边界达到.作为推论,他们给出了对应凸性的证明并且得到了用区域边界高斯曲率的下界给出的凸性估计.我们对方程(1.0.2)(或(5.0.7))陈述我们的结果. 定理5.5[67]令Ω为n中的光滑有界区域,n≥2,u为方程(1.0.2)的解.并且是严格凸函数,则函数 满足下面微分不等式 Δψ1≤0 mod (▽ψ1) inΩ, (5.0.8) 这里我们已经简写成ψ1具有局部有界系数.并且函数ψ1在边界达到极小值.因此从(5.0.8),对方程(1.0.2)的解有下面估计 (5.0.9) 这里K是边界∂Ω的高斯曲率. 推论5.6[64,67]Ω为n中的光滑有界严格凸区域,κ极小,κ极大和K是边界∂Ω的极小主曲率,极大主曲率和极小高斯曲率.如果u为方程(1.0.2)的解,并且是严格凸函数.则v的图的高斯曲率KG满足下面最优估计 (5.0.10) 如果Ω为单位球B1(0)⊂n则在(5.0.10)等号在原点O成立. 例3的相关估计. 在二维时,利用了Makar-Limanov[65]的类似技巧,Acker-Payne-Philippin[1]他们给出了Brascamp-Lieb关于凸有界区域上的第一特征函数的对数凹性的新证明.因为对于(1.0.3)的解u,则v=-logu满足 (5.0.11) 同样对方程(1.0.3)和(5.0.11),Ma-Shi-Ye在[67]中利用[65]和[1]的想法,对方程(1.0.3)和(5.0.11)也找到他们辅助函数的高维版本,证明它们的最小值在边界达到.作为推论,他们给出了对应凸性的证明并且得到了用区域边界高斯曲率的下界给出的凸性估计. 定理5.7 令Ω为n,n≥2中光滑有界凸区域,u>0为Dirichlet第一特征函数即方程(1.0.3)的正解.如果v=-logu为严格凸函数,则 满足以下微分不等式 Δψ2≤0 mod (▽ψ2) inΩ, (5.0.12) 里我们已经简写ψ2具有局部有界系数.并且函数ψ2在边界达到极小值.因此从(5.0.12),对方程(1.0.3)的解我们有下面估计 (5.0.13) 这里K是边界∂Ω的高斯曲率. 注 Andrews-Clutterbuck[5]利用与一维情形的对比,对v=-logu的凸性给出了一个最优估计从而解决了有名的特征值得Gap猜想. [1] Acker A Payne L E and Philippin G. On the converxity of level lines of the fundamental mode in the clamped membrane problem, and the existence of convex solutions in a related free boundary problem[J]. Z. Angew. math. Phys., 1981,32:683-694. [2] Ahlfors L V. Conformal invariants: topics in geometric function theory[M]. McGraw-Hill Series in Higher Mathematics, New York-Düsseldorf-Johannesburg: McGraw-Hill Book Co., 1973. [3] Alvarez O, Lasry J M and Lions P-L. Converxity viscosity solutions and state constraints[J]. J. Math. Pures Appl., 1997,76:265-288. [4] Andrews B. Noncollapsing in mean-convrx mean curvature flow[J]. Geom. Topol., 2012,16(3):1413-1418. [5] Andrews B and Clutterbuck J. Proof of the fundamental gap conjecture[J]. J. Amer. Math. Soc., 2011, 24:899-916. [6] Bian B J and Guan P F. A microscopic convexity principle for nonlinear partial differential equations[J]. Invent. Math., 2009,177(2):307-335. [7] Bian B J, Guan P, Ma X N and Xu L. A microscopic convexity principle for the level sets of solution for nonlinear elliptic partial differential equations[J]. Indiana Univ. Math. J., 2011, 60(1):101-119. [8] Bianchini C, Longinetti M and Salani P. Quasiconcave solutions to elliptic problems in convex rings[J]. Indiana Univ. Math. J., 2009, 58:1565-1590. [9] Borell C. Brownian motion in a convex ring and quasiconcavity[J]. Comm. Math. Phys., 1982, 86(1): 143-147. [10] Borell C. A note on parabolic convexity and heat conduction[J]. Ann. Inst. H. Poincarè Probab. Stat., 1996,32(3):387-393. [11] Borell C. Diffusion equations and geometric inequalities[J]. Potential Anal., 2000,12(1):49-71. [12] Brascamp H J and Lieb E H. On extensions of the Bruun-Minkowski and Prekopa-Leindler theorems, including inequalities for log-concave functions, with and application to the diffusion equation[J]. J. Funct. Anal., 1976, 22:366-389. [13] Brendle S. Embedded minimal tori inS3and the Lawson conjecture[J]. Acta Math., 2013, 211(2): 177-190. [14] Caffarelli L and Friedman A. Convexity of solutions of some semilinear elliptic equations[J]. Duke Math. J., 1985, 52: 431-455. [15] Caffarelli L, Guan P and Ma X N. A constant rank theorem for solutions of fully nonlinear elliptic equations[J]. Comm. Pure Appl. Math., 2007, 60(12):1769-1791. [16] Caffarelli L, Nirenberg L and Spruck J. Nonlinear second order elliptic equations IV: Starshaped compact Weingarten hypersurfaces[C]∥ Ohya Y,Kasahara K and Shimakura(eds) N, Kinokunize. Current topics in partial differential equations. Tokyo: 1985:1-26. [17] Caffarelli L and Spruck J. Converxity properties of solutions to some classical variational problems[J]. Comm. Partial Differ. Equations, 1982,7:1337-1379. [18] Do Carmo M P. Differential geometry of curves and surfaces[M]. Prentice-Hall, Inc., Englewood Cliffs, N. J., 1976. [19] Chang A, Ma X N, Yang P. Principal curvature estimates for the convex level sets of semilinear elliptic equations[J]. Discrete Contin. Dyn. Syst., 2010, 28(3): 1151-1164. [20] Chen C Q and Hu B W. A Microscopic Convexity Principle for Space-time Convex Solutions of DFully Nonlinear Parabolic Equations[J]. Acta Mathematica Sinica, English Series, 2013, 29(4): 651-674. [21] Chen C Q, Ma X N and Salani P. On sapce-time quasiconcave solutions of the heat equation[J]. arXiv: 1405. 6373v2, 1 Feb 2016, to appear in Memoirs of the American Mathematical Society. [22] Chen C Q and Shi S J. Curvature estimates for the level sets of spatial quasiconcave solutions to a class of parabolic equations[J]. Sci. China Math., 2011, 54(10): 2063-2080. [23] Colesanti A. Brunn-Minkowski inequalities for variational functionals and related problems[J] Advance in Mathematics, 2005, 194: 105-140. [24] Colesanti A and Salani P. Quasi-concave envelope of a function and convexity of level sets of solutions to elliptic equations[J] Math. Nachr., 2003, 258:3-15. [25] Daskalopoulos P, Hamilton R and Lee K. All timeC∞-regularity of interface in degenerated diffusion: A geometric approach[J]. Duke Math. J., 2001, 108(2):295-327. [26] Diaz J I and Kawohl B. On convexity and starshapedness of level sets for some nonlinear elliptic and parabolic problems on convex rings[J]. Preprint n. 393(1986), Sonderforschungsbereich 123, Universität Heidelberg. Available at http:∥www.mi.uni-koeln.de/~kawohl. [27] Diaz J I and Kawohl B. On convexity and starshapedness of level sets for some nonlinear elliptic and parabolic problems on convex rings[J]. J. Math. Anal. Appl., 1993, 177:263-286. [28] Gabriel R. A result concerning convex level surfaces of 3-dimensional harmonic functions[J]. J. London Math. Soc., 1957, 32:286-294. [29] Gergen J. Note on the Green Function of a Star-shaped Three Dimensional Region[J]. Amer. J. Math., 1931, 53(4):746-752. [30] Greco A and Porru G. Convexity of solutions to some elliptic partial differential equations[J]. SIAM J. Math. Anal., 1993, 24:833-839. [31] Guan P, Li Q and Zhang X. A uniqueness theorem in Kahler geometry[J]. Maht. Ann., 2009, 345:377-393. [32] Guan P, Lin C S and Ma X N. The Christoffel-Minkowski problem II. Weingarten curvature equations[J]. Chinese Ann. Math. Ser. B, 2006, 27(6):595-614. [33] Guan P, Lin C S and Ma X N. The exsitence of convex body with prescribed curvature measures[J]. Int. Math. Res. Not. IMRN,2009(11):1947-1975. [34] Guan P and Ma X N. Christoffel-Minkowski Problem I: Convexity of Solutions of a Hessian Equations[J]. Inventiones Math., 2003, 151:553-577. [35] Guan P, Ma X N and Zhou F. The Christofel-Minkowski problem III. Existence and convexity of admissible solution[J]. Comm. Pure Appl. Math., 2006,59(9):1352-1376. [36] Guan P, Xu L. Convexity estimates for level sets of quasiconcave solutions to fully nonlinear elliptic equations[J]. J. Reine Anges. Math., 2013, 680:41-67. [37] Hamel F, Nadirashvill N and Sire Y. Convexity of level sets for elliptic problems in convex domains or convex rigns: two counterexamples[J]. Amer. J. Math., 2016, 138(2): 499-527. [38] Han F, Ma X N and Wu D M. The existence of k-convex hypersurface with prescribed mean curvature[J]. Cal. Var. Partial Diferential Equations, 2011, 42(1-2): 43-72. [39] Hu B W and Ma X N. Constant rank theorem of the space-time convex solution of heat equation[J]. Manu. Math., 2012, 138(1-2): 89-118. [40] H C Q, Ma X N and Ou Q Z. A constant rank theorem for level sets of immersed hypersurfaces inn+1with prescribed mean curvature[J]. Pacific J. Math., 2010, 245(2): 255-271. [41] Hu C Q, Ma X N and Shen C L. On the Christoffel-Minkowski problem of Firey’sp-sum[J]. Calc. Var. Partial Differential Equation, 2004, 21(2):137-155. [42] Ishige K and Salani P. Is quasi-concavity preserved by heat flow[J]. Arch. Math. (Basel), 2008,90(5):450-460. [43] Ishige K and Salani P. Parabolic quasi-concavity for solutions to parabolic problems in convex rigns[J]. Math. Nachr., 2010, 283(11):1526-1548. [44] Ishige K and Salani P. On a new kind of convexity for solutions of parabolic problems[J]. Discrete Contin. Dyn. Syst. Ser., 2011,S 4: 851-864. [45] Ishige K and Salani P. Parabolic power concavity and parabolic boundary value problems[J]. Math. Ann., 2014, 358(3-4): 1091-1117. [46] Ishige K and Salani P. Parabolic Minkowski convolutions of solution to parabolic boundary value problems[J]. Adv. Math., 2016,287:640-673. [47] Ishige K, Nakagawa K and Salani P. Poer concavity in weakly coupled elliptic and prabolic systems[J]. Nonliear Anal., 2016,131:81-97. [48] Jost J, Ma X N and Ou Q Z. Curvature estimates in dimensions 2 and 3 for the level sets ofp-harmonic functions in convex rings[J]. Trans. Amer. Math. Soc., 2012, 364:4605-4627. [49] Kawohl B. Rearrangements and convexity of level sets in PDE. Lectures Notes in Math.[M]. Berlin:Springer-Verlag, 1985:1150. [50] Kawohl B. A remark on N.Korevaar’s concavity maximum principle and on the asymptotic uniqueness of solutions to the plasma problem[J]. Math. Methods Appl. Sci., 1986, 8:93-101. [51] Kennington A U. Power concavity and boundary value problems[J]. Indiana Univ. Math. J., 1985,34:687-704. [52] Kennington A U. Convexity of level curves for an initial value problem[J]. J. Math. Anal. Appl., 1988,133:324-330. [53] Korevaar N. Capillary surface convexity above convex domains[J]. Indiana Univ. math. J., 1983, 32: 73-81. [54] Korevaar N. Convex solutions to nonlinear elliptic and parabolic boundary value problems[J]. Indiana Univ. math. J., 1983,32:603-614. [55] Korevaar N. Convexity of level sets for solutions to elliptic ring problems[J]. Comm. Partial Differ. Equations, 1990, 15(4): 541-556. [56] Korevaar N and Lewis J. Convex solutions of certain elliptic equations have constant rank hessians[J]. Arch. Rational Mech. Anal., 1987, 91:19-32. [57] Lee K A and Vazquez J L. Parabolic approach to nonlinear elliptic eigenvalue problems[J]. Advances in mathematics, 2008, 219: 2006-2028. [58] Lewis J L. Capacitary functions in convex rings[J]. Arch. Rational Mech. Anal., 1977, 66:201-224. [59] Liu P, Ma X N and Xu L. A Brunn-Minkowski inequality for the Hessian eigenvalue in three-dimensional convex domain[J]. Adv. Math., 2010, 225(3):1616-1633. [60] Longinetti M. Convexity of the level lines of harmonic functions[J]. (Italian) Boll. Un. Math. Ital., 1983, A 6: 71-75. [61] Longinetti M. On minimal surfaces bounded by two convex curves in prarllel planes[J]. J. Diff. Equations, 1987, 67:344-358. [62] Longinetti, Marco. A strict convexity principle for nonlinear elliptic equations[J]. preprint, 2006. [63] Longinetti M and Salani P. On the Hessian matrix and Minkowski addition of quasiconvex functions[J]. J. Math. Pures Appl., 2007, (9)88(3): 276-292. [64] Ma X N. Concavity estimates for a class of nonlinear elliptic equations in two dimensions[J]. Math. Zeit., 2002, 240: 1-11. [65] Makar-Limanov L G. Solution of Dirichlet’s problem for the equationΔu=-1 on a convex region[J]. Math. Notes Acad. Sci., 1971, USSR 9: 52-53. [66] Ma X N, Ou Q Z and Zhang W. Gaussian curvature estimates for the convex level sets ofp-harmonic functions[J]. Comm. Pure Appl. Math., 2010, 63(7):935-971. [67] Ma X N, Shi S J and Ye Y. The Convexity Estimates for the Solutions of Two Elliptic Eqautions[J]. Comm. Partial Differ. Equations, 2012, 37(12): 2116-2137. [68] Ma X N and Xu L. The convexity of solution of a class Hessian equation in bounded convex domain in3[J]. J. Funct. Anal., 2008, 255(7): 1713-1723. [69] Ma X N and Zhang W. The concavity of the Gaussian curvature of the convex level sets ofp-harmonic functions with respect tot he height[J]. Commun. Math. Stat., 2013,1(4): 465-489. [70] Ma X N and Zhang Y. The convexity and Gaussian curvature estimates for the level sets of harmonic functions on convex rings in space forms[J]. The journal of Geometric Analysis, 2014, 24(1): 337-374. [71] Ortel M and Schneider W. Curvature of level curves of harmonic functions[J]. Canad. Math. Bull., 1983, 26(4): 399-405. [72] Salani P. Convexity of solutions and Brunn-Minkowski inequalities for Hessian equations in3[J]. Advances in Mathematics, 2012, 229:1924-1948. [73] Schneider R. Convex bodies: The Brunn-Minkowski theory[M]. Cambridge University, 1993. [74] Sheng W M and Wang W J. Singularity profile in the mean cruvature flow[J]. Methods Appl. Anal., 2009,16(2):139-155. [75] Shi S J. Convexity estimates for the Green’s function[J]. Cal. Var. Partial Differential Equations, 2015, 53(3-4):675-688. [76] Shiffman M. On surfaces of stationary area bounded by two circles, or convex curves, in parallel planes[J]. Annals of Math., 1956, 63:77-90. [77] Singer I, Wong B, Yau S T and Stephen S T. Yau. An estimate of gap of the first two eigenvalues in the Schrodinger operator[J]. Ann. Scuola Norm. Sup. Pisa Cl. Sci., 1985, 12(4):319-333. [78] Talenti G. On functions, whose lines of steepest descent bend proportionally to level lines[J]. Ann. Scuola Norm. Sup. Pisa Cl. Sci., 1983, 10(4):587-605. [79] Wang G F and Xia C. Isoperimetric type problems and Alexandrov-Fenchel type inequalities in the hyperbolic space[J]. Advances in Mathematics, 2013, 259(10):532-556. [80] Wang P H. The concavity of the Gaussian curvature of the convex level sets of mini-mal surfaces with respect to the height[J]. Pacific Journal of Mathematics, 2014, 267(2):489-509. [81] Wang P H and Zhang W. Gaussian curvature estimates for the convex level sets of solutions for some nonlinear elliptic partial differential equations[J]. J. Partial Differ. Equ., 2012, 25(3): 239-275. [82] Wang X J. Counterexample toe the convexity of level sets of solutions to the mean curvature equation[J]. European Mathematical Society Journal, 2014, 16(6): 1173-1182. [83] Xu L. A Microscopic convexity theorem of level sets for solutions to elliptic equations[J]. Cal. Var. Partial Differential Equations, 2011, 40(1-2): 51-63. 麻希南教授简介 麻希南教授 1969年1月出生于浙江省嵊县,1996年获杭州大学基础数学博士学位.现任中国科学技术大学数学科学学院教授. 先后在华东师范大学、中国科学技术大学、中科院数学研究所、加拿大McMaster大学、以色列Bar-Ilan大学、台湾理论科学中心、澳大利亚国立大学、德国马普数学研究所、美国普林斯顿高等研究院等地工作和访问.曾经得到过霍英东青年教师奖(2004);中国科学院百人计划(2005);国家自然科学基金委员会国家杰出青年基金(2011);教育部长江学者(2013)等奖励与资助.主持多项国家自然科学基金,发表多篇高水平论文. 主要研究非线性椭圆偏微分方程和几何分析.与人合作在凸体理论中的Christoffel-Minkowski问题,最优运势问题的存在性与正则性,椭圆Hessian方程的Neumann问题,Kahler流形上的非线性椭圆偏微分方程,椭圆与抛物方程解的凸性以及水平集凸性等问题上做过工作. The Convexity of the Solution of Elliptic and Parabolic Partial Differential Equations MAXi-nan (School of Mathematical Sciences, University of Science and Technology of China, Hefei 230026, China) We give a survey on the convexity of the solutions or the level sets of the solution for elliptic and parabolic partial differential equations. We start three classical examples,then we introduce some usual methods in the study of convexity, at last we get some quantitative convexity estimates. We mainly concerns the results obtained by the author and his collaborator. The convexity of the solution for partial differential equations; the convexity of the level sets of the solution of partial differential equations; constant rank theorem; convexity estimates for the solution and its level sets 2016-09-30; [修改日期]2016-10-10 国家自然科学基金(11471188;11125105) 麻希南(1969—)男,博士,教授,从事偏微分方程研究.Emal: xinan@ustc.edu.cn 175.25 A 1672-1454(2016)05-0001-17


2 偏微分方程解的凸性


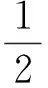
3 偏微分方程解水平集的凸性



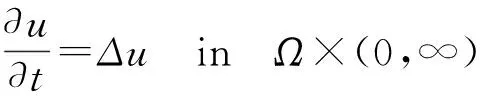
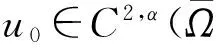
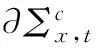

4 凸环上调和函数水平集的严格凸性




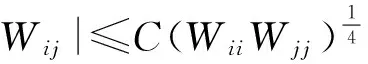
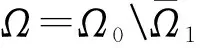

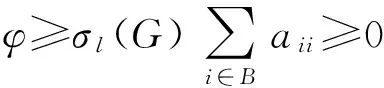

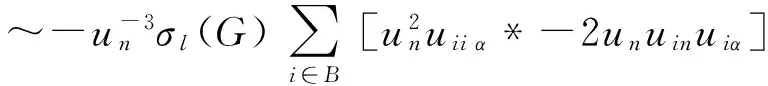


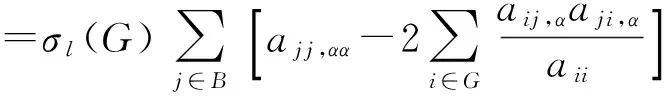

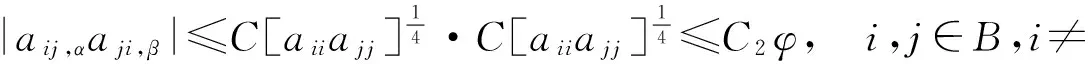
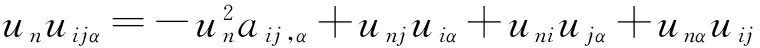
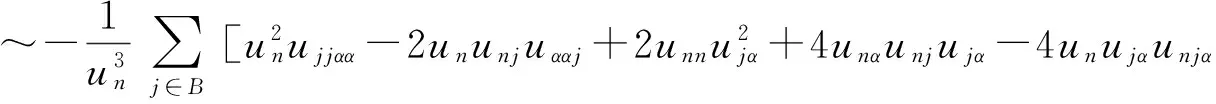
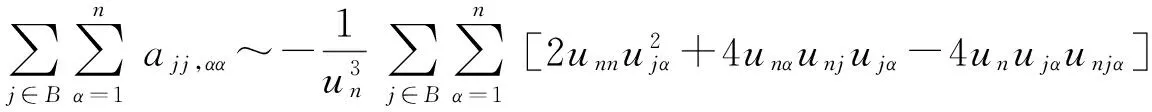

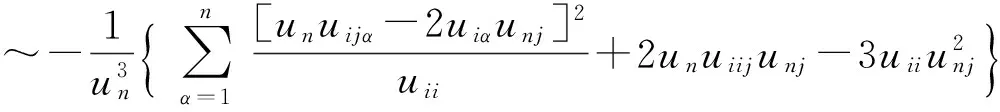
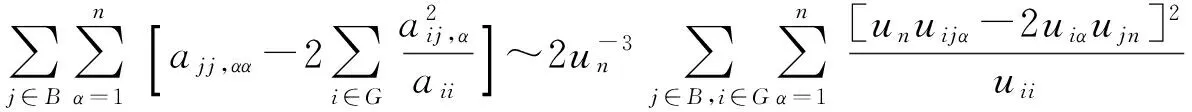


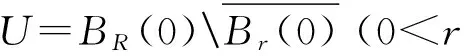
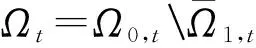

5 解与水平集凸性的定量估计