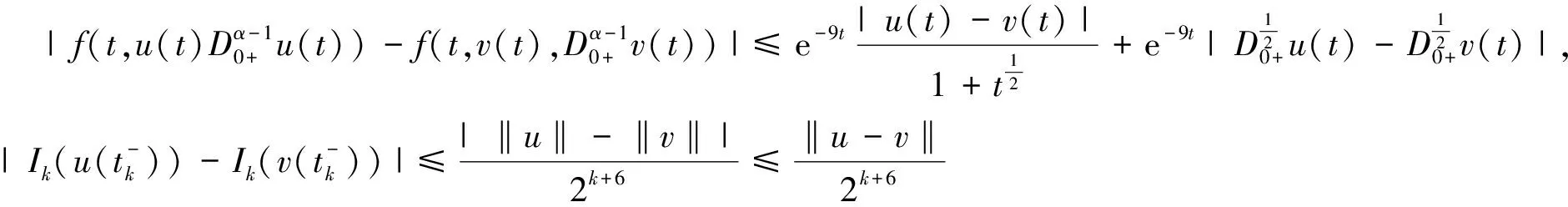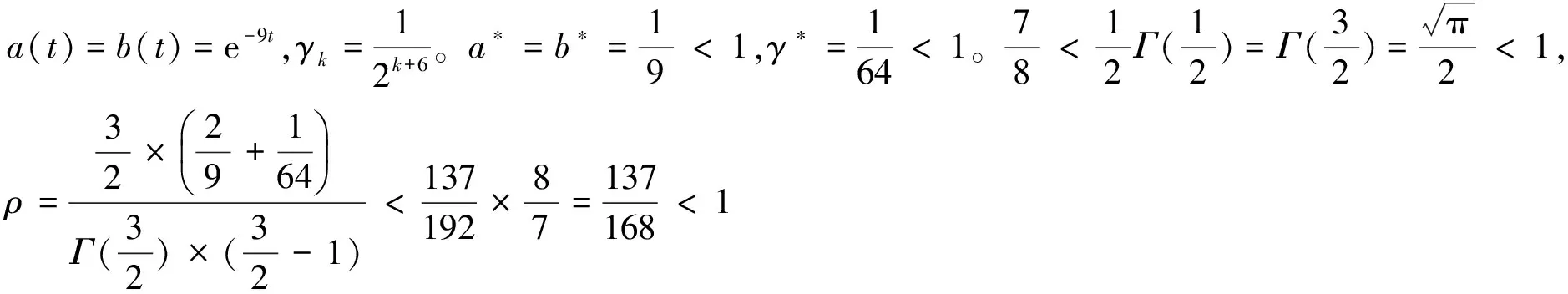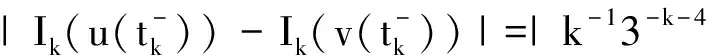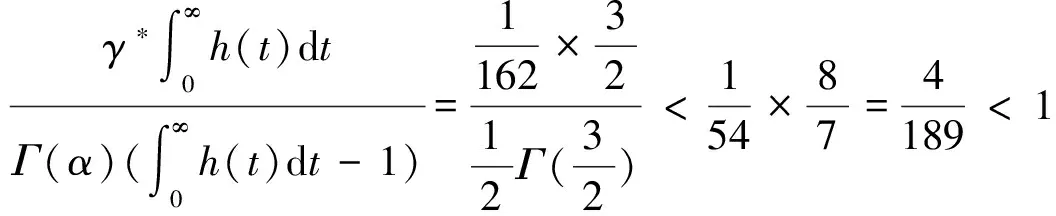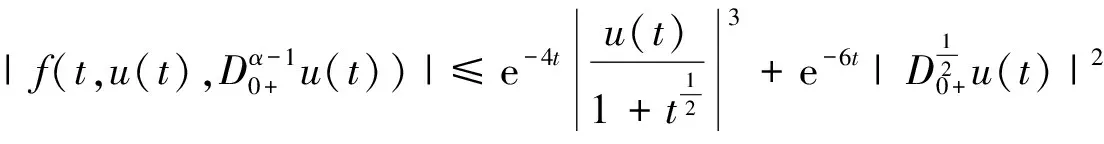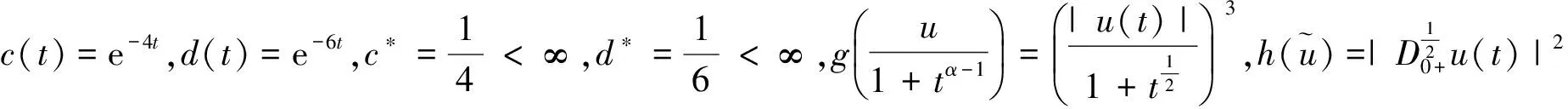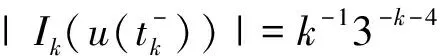分数阶脉冲微分方程边值问题解的存在性
江卫华,李庆敏,周彩莲
(河北科技大学理学院,河北石家庄 050018)
分数阶脉冲微分方程边值问题解的存在性
江卫华,李庆敏,周彩莲
(河北科技大学理学院,河北石家庄 050018)
为了解决对半无穷区间上具有可数个脉冲点且带有积分边界条件的分数阶脉冲微分方程边值问题,具体研究此类微分方程边值问题解的存在性。通过定义合适的Banach空间、范数以及算子,合理运用分数阶微积分的性质,分别应用压缩映像原理和Krasnoselskii不动点定理证明了分数阶脉冲微分方程边值问题解的存在性,最后通过实例验证了此类方程边值问题解的存在性。
常微分方程解析理论;脉冲;压缩映像原理;Krasnoselskii不动点定理;边值问题;半无穷区间
1 问题提出
分数阶微积分是对整数阶微积分理论的拓展,它可以更好地描述某些客观事物或规律,应用广泛,比如在处理光学和热学系统、流变学及材料和力学系统、信号处理和系统辨识、控制等问题的过程中,经常会用到分数阶微积分的理论。所以分数阶微积分理论受到了人们越来越多的关注[1-12]。此外,脉冲微分方程也有广泛的应用,许多学者对脉冲微分方程的理论及其应用[13-24]进行了深入的研究。
文献[2]中GUO应用Banach空间中的锥拉伸与压缩不动点定理研究了半无穷区间上具有可数个脉冲点的二阶奇异脉冲微分方程边值问题:
解的存在性。
文献[4]中AHMAD等根据压缩映像原理和Krasnoselskii不动点定理研究了有限区间上具有有限个脉冲点的非线性分数阶脉冲微分方程边值问题:
解的存在性。
受上述文献的启发,本文将应用压缩映像原理和Krasnoselskii不动点定理研究半无穷区间上具有可数个脉冲点的分数阶脉冲微分方程边值问题:
2 预备知识
定义1u:J→R是连续函数,u的α阶Riemann-Liuville积分的定义式为
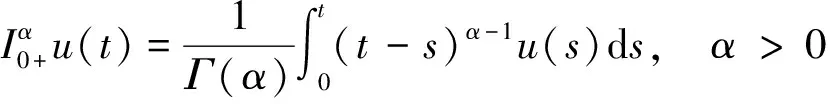
定义2u:J→R是连续函数,u的α阶Riemann-Liuville导数的定义式为
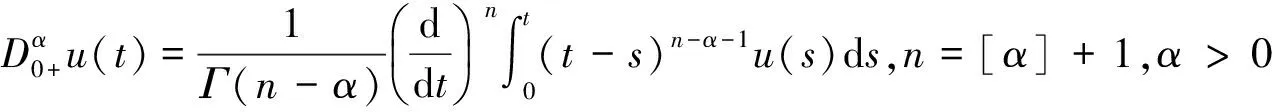
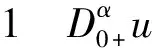
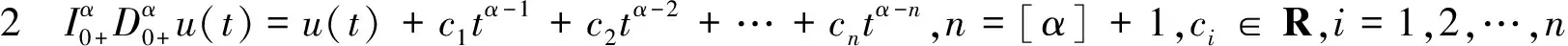
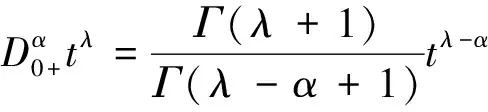
定理1 (压缩映像原理)
设X是完备的度量空间,T是X上的压缩映像,那么T有且仅有1个不动点。
定理2 (Krasnoselskii不动点定理)
设M是Banach空间X中的一个非空凸闭子集。假设A,B是2个算子,满足:
a) 对任意的x,y∈M,有Ax+By∈M;
b)A是全连续映射;
c)B是一个压缩映射,
则至少存在一个z∈M,使得z=Az+Bz。
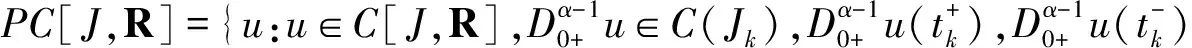
引理4 对于给定的函数y∈C(Jk),k=1,2,…,u(t)是分数阶脉冲微分方程边值问题:
的解当且仅当u(t)满足
证明 设u(t)是分数阶脉冲微分方程边值问题(2)的解,由引理2可得当t∈[0,t1]时,
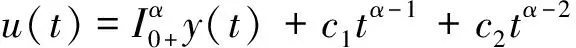
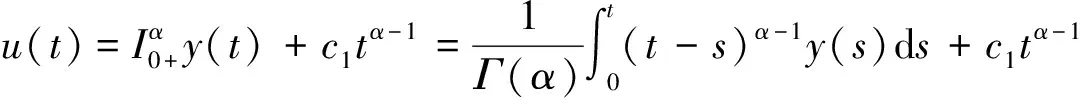
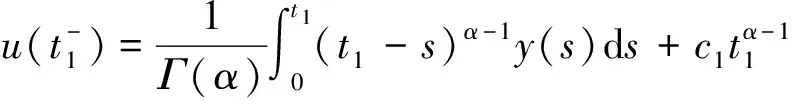
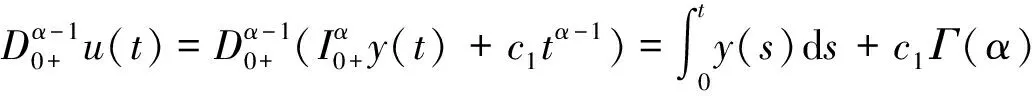
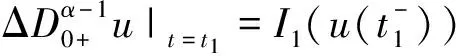
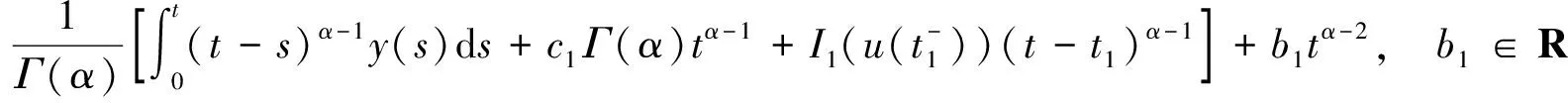
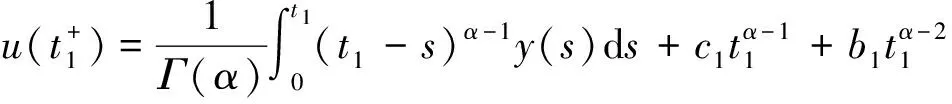
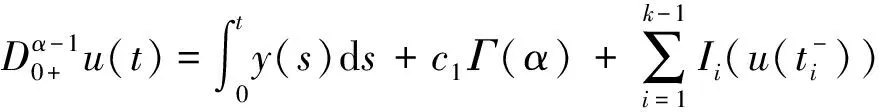
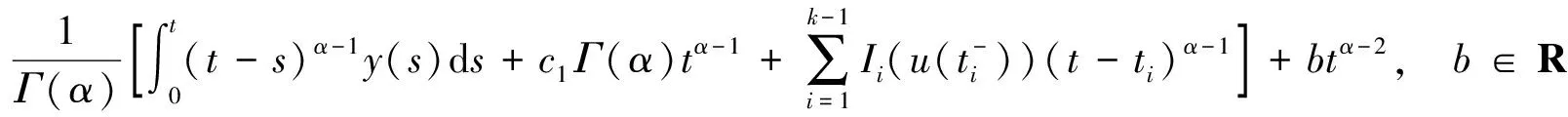
同理由u(t)的连续性可知b=0,所以t∈Jk=(tk-1,tk]时,
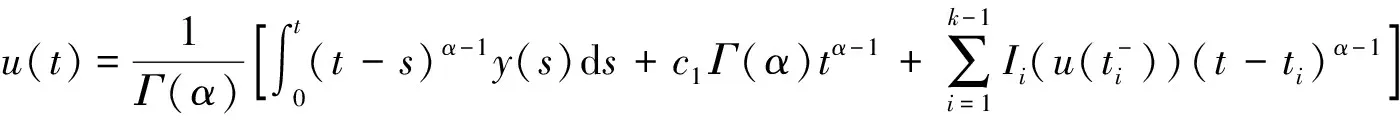
因此,对∀t∈J有
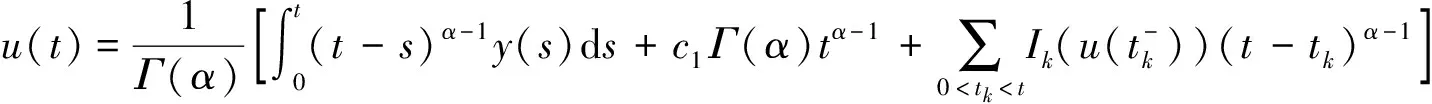
(4)
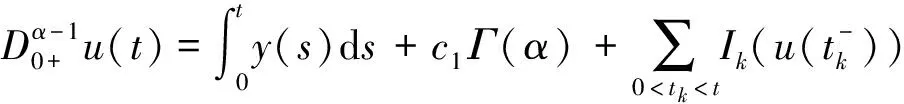
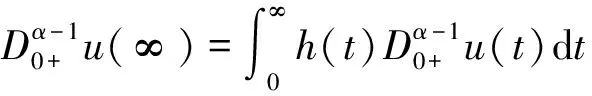
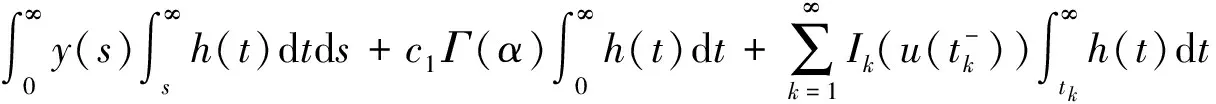
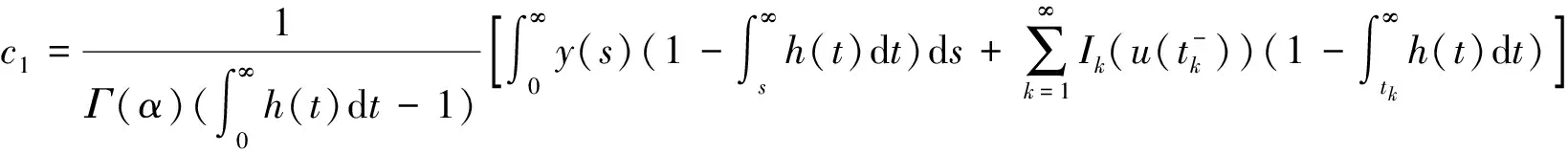
3 主要结果
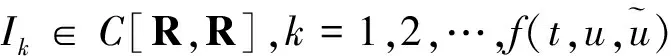
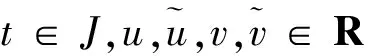
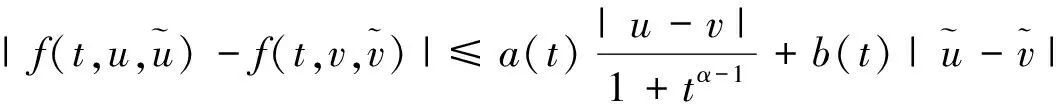
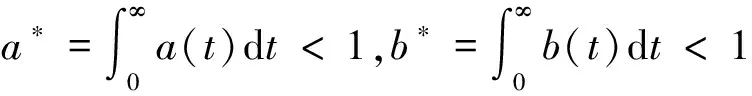
H2)存在常数γk∈J,使得对∀t∈J,u,v∈R,有
|Ik(u)-Ik(v)|≤γk‖u-v‖,
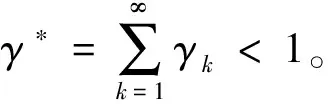
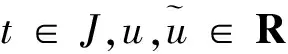
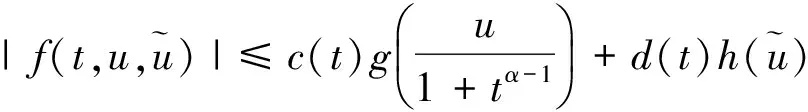
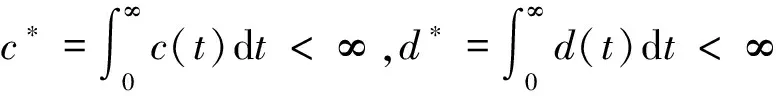
H4)存在函数F∈C[R,J],常数ηk∈J,使得对∀t∈J,u∈R,有
|Ik(u)|≤ηkF(u),
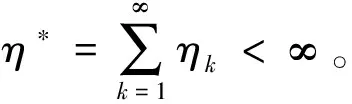
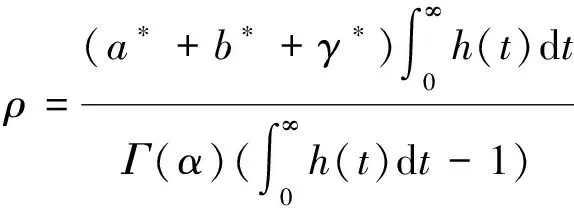
证明 定义算子T:PC1[J,R]→PC1[J,R]如下:
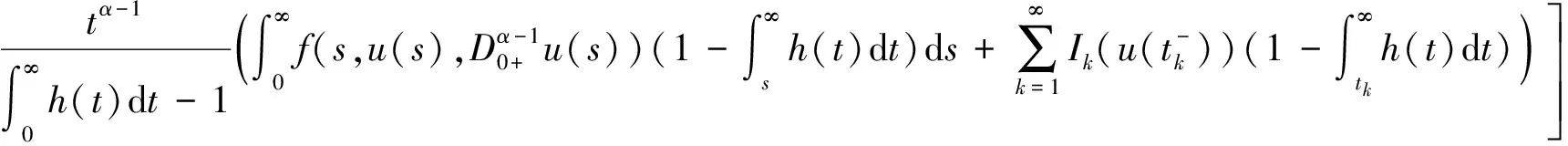
所以
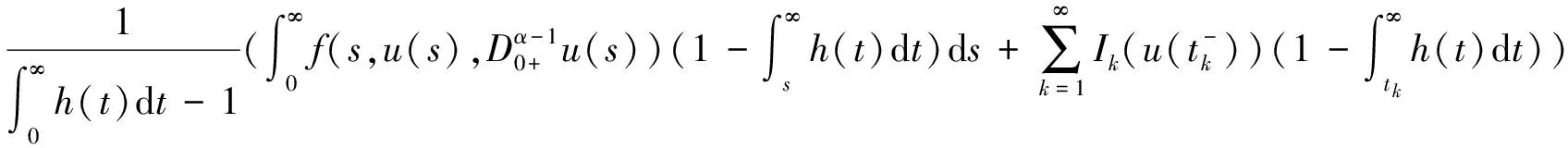
对∀u,v∈PC1[J,R],∀t∈J有
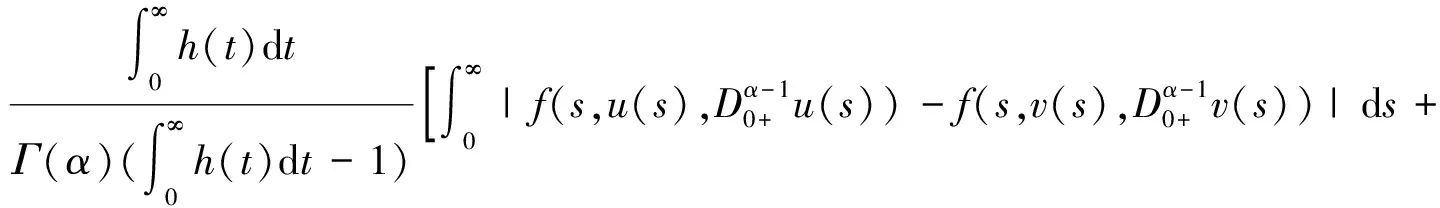
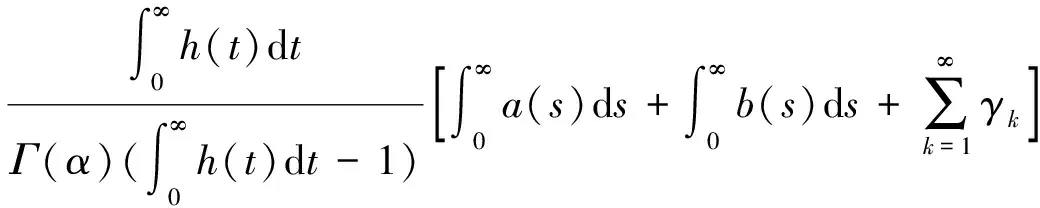
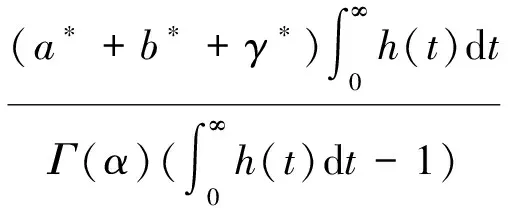
所以‖Tu-Tv‖S≤ρ‖u-v‖。
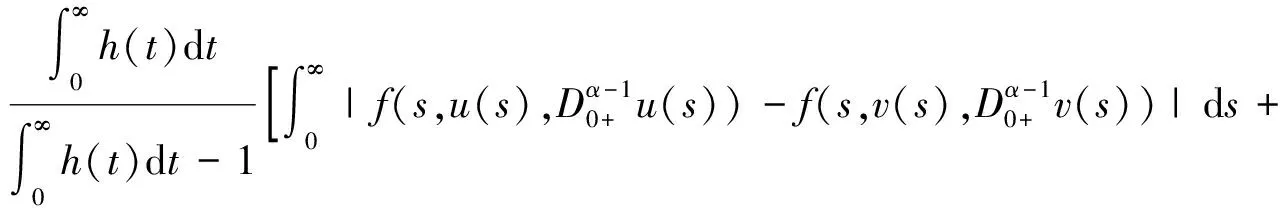
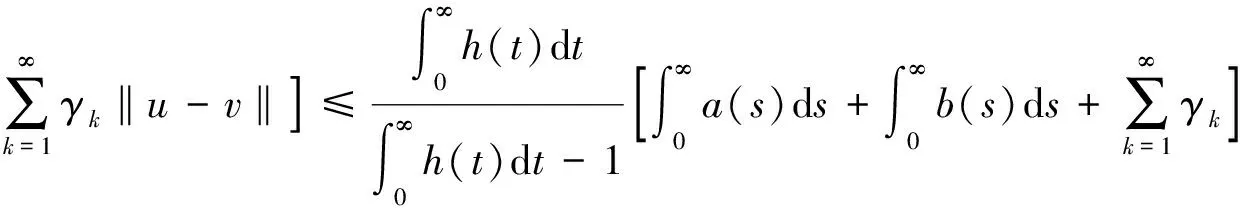
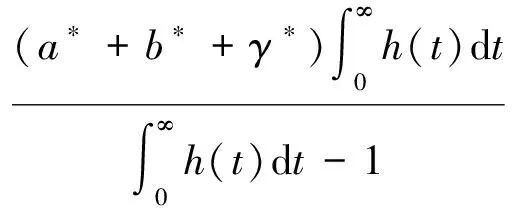
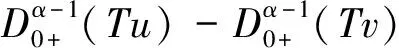
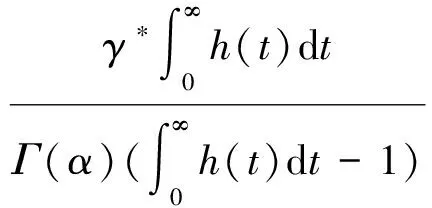
证明 定义算子如下:
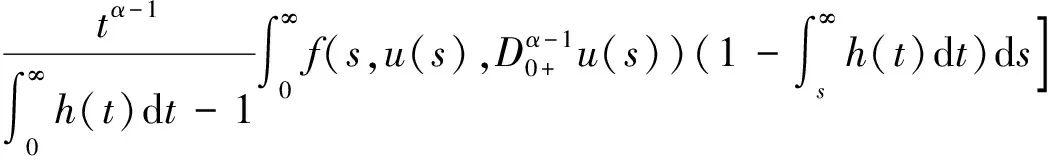
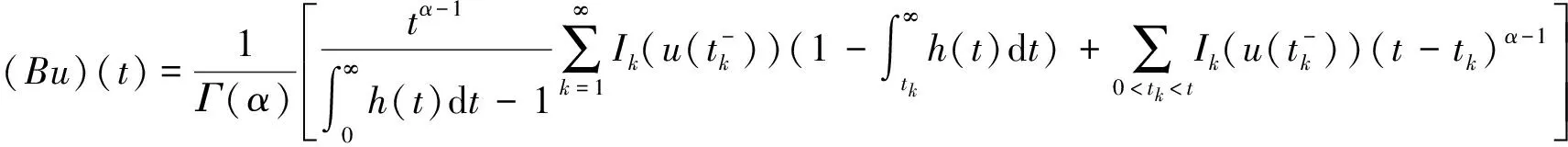
所以
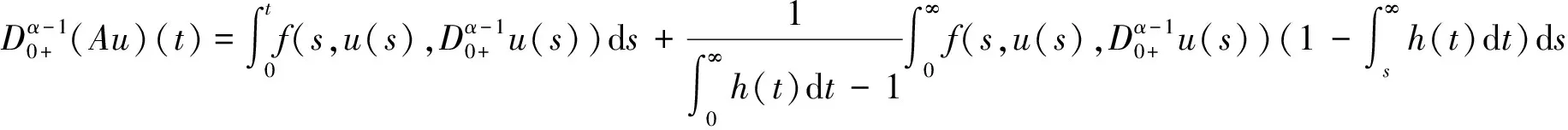
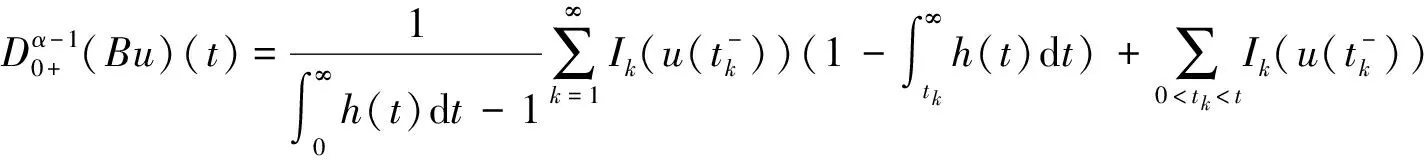
由条件H3)—条件H4)可知:对∀r>0,
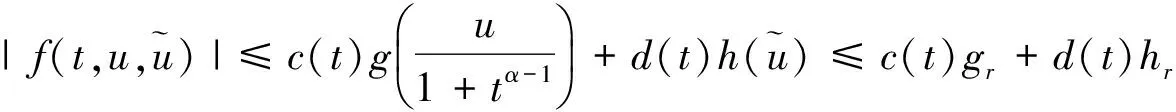
|Ik(u)|≤ηkF(u)≤Nηk,k=1,2,…,
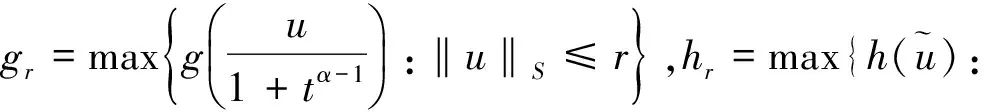
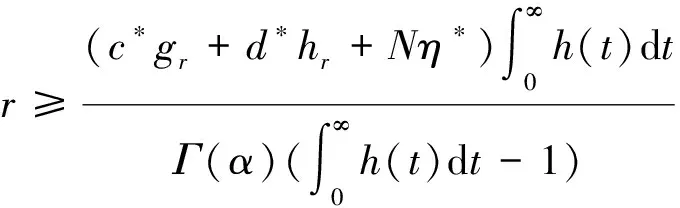
对∀u,v∈Br,∀t∈J,
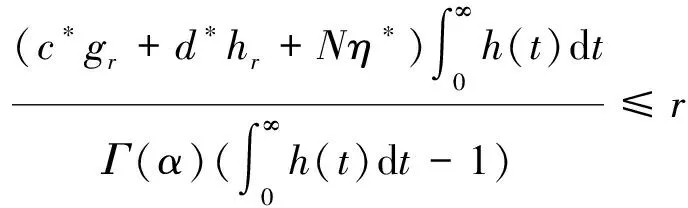
所以‖Au+Bv‖S≤r。
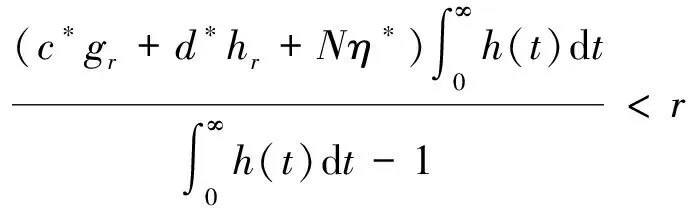
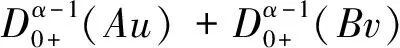
下证Bu为压缩算子。对∀u,v∈Br,∀t∈J有
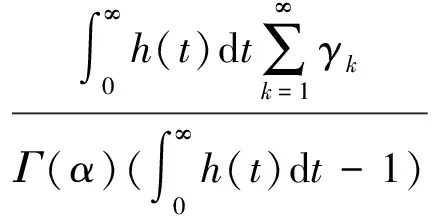
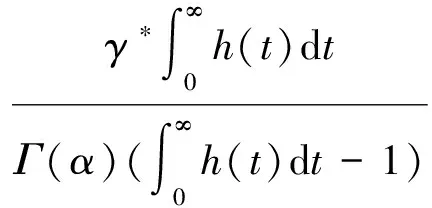
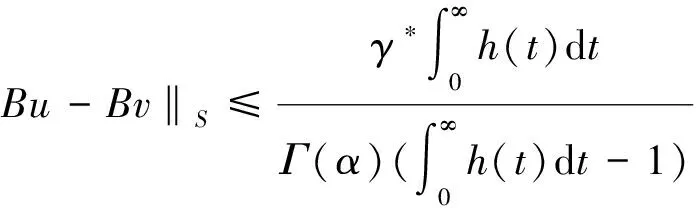
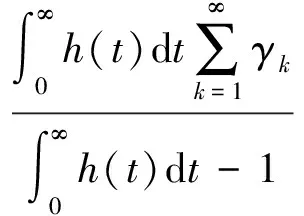
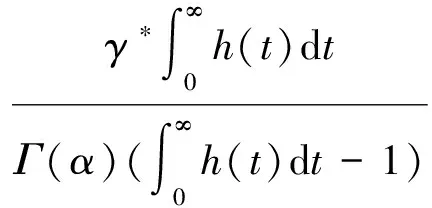
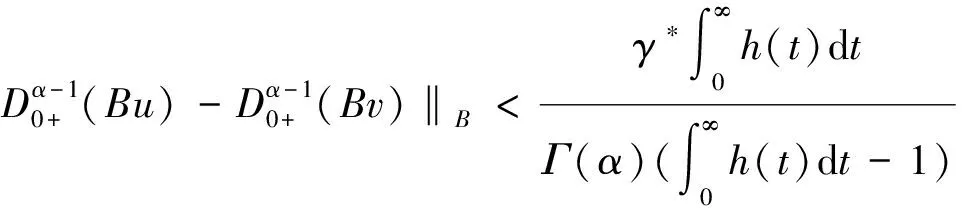
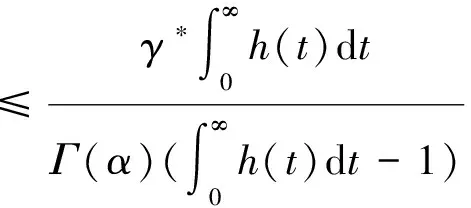
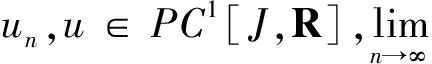
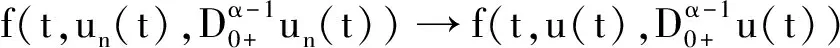

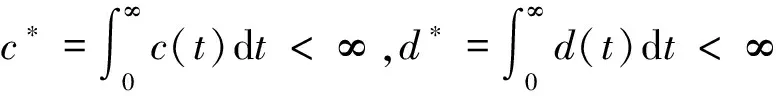
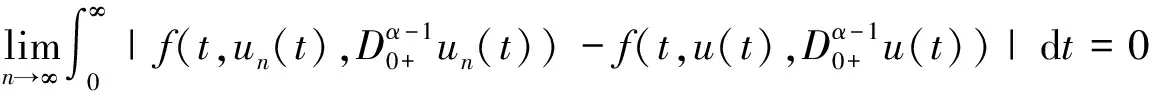
对∀t∈J,
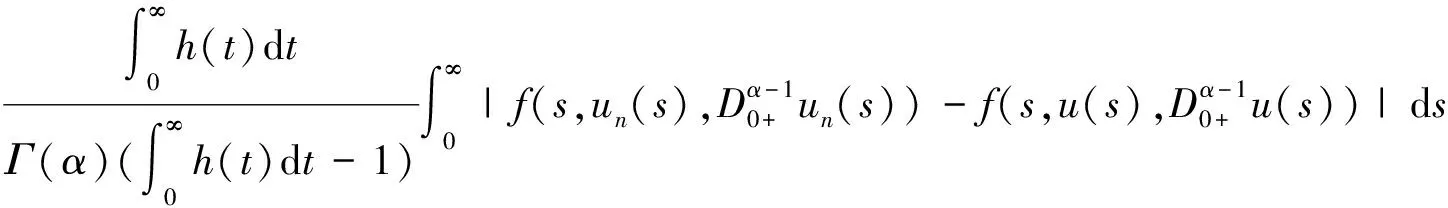
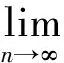
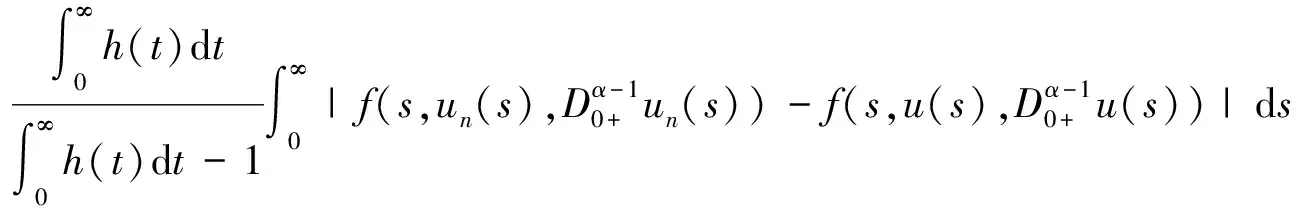
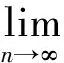
下证算子A的紧性。取un∈Br={u∈PC1[J,R]:‖u‖≤r}。对∀t∈J,
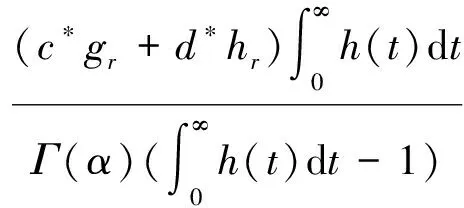
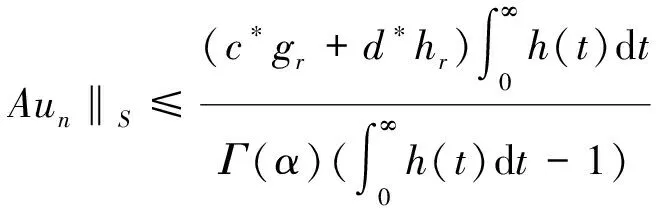
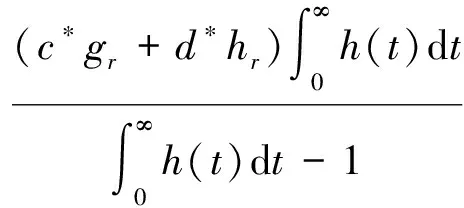
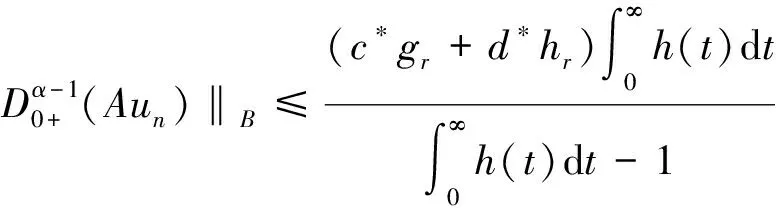
定义函数
对∀t1,t2∈Jk,当t2>t1时,有
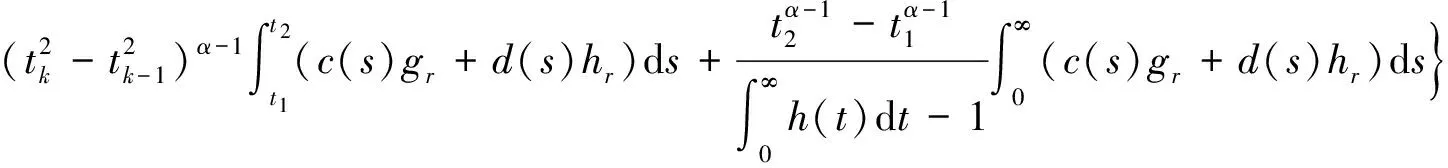
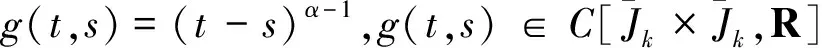
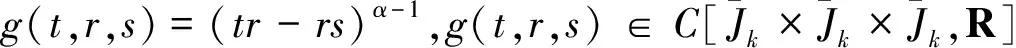
由积分的绝对连续性可知:存在δ3,使得|t2-t1|<δ3时,
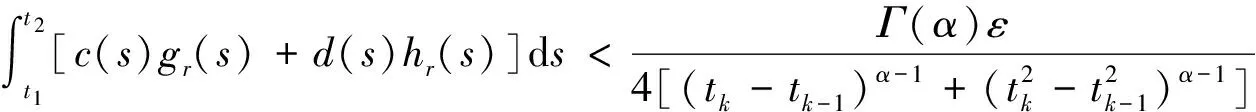
由一元连续函数的一致连续性可知:存在δ4,使得|t2-t1|<δ4时,
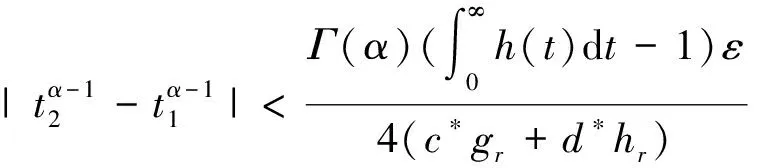
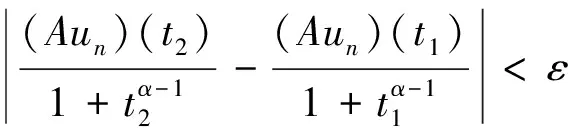
令
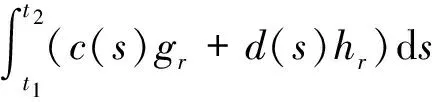
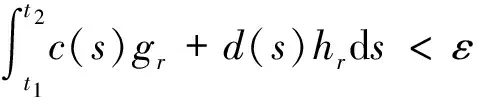
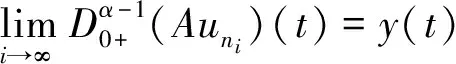
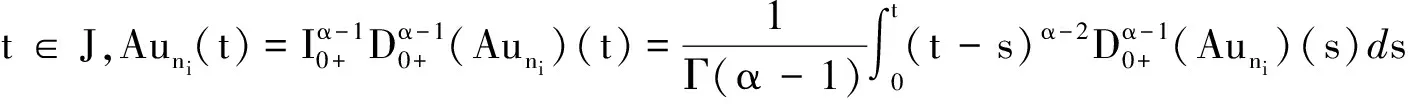
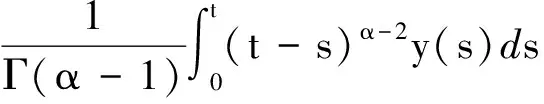
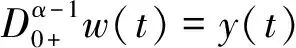
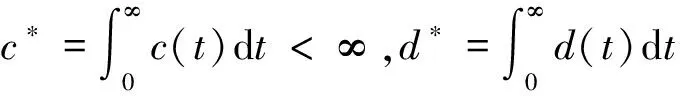
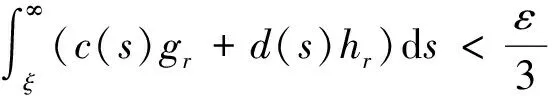
对∀ξ 对∀ξ 例1 考虑半无穷区间上分数阶脉冲微分方程边值问题 例2 考虑半无穷区间上分数阶脉冲微分方程边值问题 因此,根据定理4可得该分数阶脉冲微分方程边值问题至少有1个解。 [1] GUO Dajun. Multiple positive solutions for first order impulsive singular integro-differential equations on the half line[J]. Acta Mathematica Scientia, 2012, 32B(6): 2176-2190. [2] GUO Dajun. Existence of two positive solutions for a class of second order impulsive singular integro-differential equations on the half line in banach spaces[J]. Boundary Value Problems, 2016(1):1-31. [3] AHMAD B, SIVASUNDARAM S. Existence of solutions for impulsive integral boundary value problems of fractional order[J]. Nonlinear Analysis: Hybrid Systems, 2010, 4(1):134-141. [4] AHMAD B, SIVASUNDARAM S. Existence results for nonlinear impulsive hybrid boundary value problems involving fractional differential equations[J]. Nonlinear Analysis: Hybrid Systems, 2009, 3(3): 251-258. [5] 江卫华, 李海明. 分数阶脉冲微分方程组边值问题解的存在性[J]. 河北科技大学学报, 2015, 36(2): 134-143. JIANG Weihua, LI Haiming. Existence of solutions for boundary value problem of fractional order impulsive differential equations systems[J]. Journal of Hebei University of Science and Technology, 2015, 36(2): 134-143. [6] REHMAN M, ELOE P. Existence and uniqueness of solutions for impulsive fractional differential equactions[J]. Applied Mathematics & Computation, 2013, 224(1): 422-431. [7] 许晓婕, 孙新国, 吕炜. 非线性分数阶微分方程边值问题正解的存在性[J]. 数学物理学报, 2011, 31A(2): 401-409. XU Xiaojie, SUN Xinguo, LYU Wei. Existence of positive solutions for boundary value problems with nonlinear fractional differential equations[J]. Acta Mathematica Scientia, 2011, 31A(2): 401-409. [8] LIU Zhenhai, LI Xiuwen. Existence and uniqueness of solutions for the nonlinear impulsive fractional differential equactions[J]. Communications in Nonlinear Science and Numerical Simulation, 2013, 18(6): 1362-1373. [9] WANG Jinrong, ZHOU Yong, FECKAN M. On recent developments in the theory of boundary value problems for impulsive fractional differential equactions[J]. Computers & Mathematics with Applications, 2012, 64(10): 3008-3020. [10] CAO Jianxin, CHEN Haibo. Impulsive fractional differential equactions with nonlinear boundary conditions[J]. Mathematical and Computer Moelling, 2012, 55(3/4): 303-311. [11] GUO Tianliang,WEI Jiang. Impulsive problems for fractional differential equactions with boundary value conditions[J]. Computers & Mathematics with Applications, 2012, 64(10): 3281-3291. [12] BAI Zhanbing, LYU Haishen. Positive solutions for boundary value problem of nonlinear fractional differential equation[J]. Journal of Mathematical Analysis and Applications, 2005, 311(2): 495-505. [13]张爱华, 胡卫敏. 非线性分数阶脉冲微分方程边值问题的解[J]. 数学的实践与认识, 2014, 44(6): 233-240. ZHANG Aihua, HU Weimin. Solutions for a boundary value problem of nonlinear impulsive fractional differential equations[J]. Mathematics in Practice and Theory, 2014, 44(6): 233-240. [14]董雪. 非线性分数阶脉冲微分方程边值问题解的存在性[J]. 山东理工大学学报(自然科学版), 2015, 29(4): 70-74. DONG Xue. Existence of solutions for impulsive nonlinear fractional differential equations boundary value problems[J]. Journal of Shandong University of Technology(Natural Science Edition), 2015, 29(4): 70-74. [15]GUO Dajun. Existence of solutions of boundary value problem for nonlinear second order impulsive differential equations in banach space[J]. Journal of Mathematical Analysis and Applications, 1994, 181(2):407-421. [16]杜珺. 二阶脉冲微分方程边值问题解的存在性[J]. 生物数学学报, 2012, 27(2): 311-321. DU Jun. The existence result of solution to boundary value problem of a class of second-order impulsive differential equation[J]. Journal of Biomathematics, 2012, 27(2): 311-321. [17] HERRERO M A, VAZQUEZ J L. On the propagation properties of a nonlinear degenerate parabolic equation[J]. Communications in Partial Differential Equations, 1982, 7(12): 1381-1402. [18]ESTEBAN J R,VAZQUEZ J L. On the equation of the turbulent filtration in one-dimensional porous media[J]. Nonlinear Analysis, 1986, 10(11):1305-1325. [19] KAUL S, LAKSHMIKANTHAM V, LEELA S. Extremal solutions comparison principle and stability criteria for impulsive differential equations with variable times[J]. Nonlinear Analysis Theory Methods & Applications, 1994, 22(10): 1263-1270. [20] GUO Dajun. A class of second order impulsive integro-differential equations on unbounded domain in a banach space[J]. Applied Mathematics & Computation, 2002, 125(1): 59-77. [21]YAN Baoqiang. Boundary value problems on the half -line with impulses and infinite delay[J]. Journal of Mathematical Analysis & Applications, 2001, 259(1): 94-114. [22] LIANG Sihua, ZHANG Jihui. The existence of countably many positive solutions for some nonlinear singular there-point impulsive boundary value problems[J]. Nonlinear Analysis, 2009, 71(10): 4588-4597. [23] GUO Dajun. Variational approach to a class of impulsive differential equations[J]. Boundary Value Problems, 2014,2014(1):1-10. [24] ZHAO Yulin, CHEN Haibo. Multiplicity of solutions to two-point boundary value problems for second-order impulsive differential equations[J]. Applied Mathematics & Computation, 2008, 206(206): 925-931. Existence of solutions to boundary value problem of fractional differential equations with impulsive JIANG Weihua, LI Qingmin, ZHOU Cailian (School of Science, Hebei University of Science and Technology, Shijiazhuang, Hebei 050018, China) In order to solve the boundary value problem of fractional impulsive differential equations with countable impulses and integral boundary conditions on the half line, the existence of solutions to the boundary problem is specifically studied. By defining suitable Banach spaces, norms and operators, using the properties of fractional calculus and applying the contraction mapping principle and Krasnoselskii's fixed point theorem, the existence of solutions for the boundary value problem of fractional impulsive differential equations with countable impulses and integral boundary conditions on the half line is proved, and examples are given to illustrate the existence of solutions to this kind of equation boundary value problems. analytic theory of ordinary differential equation; impulse; contraction mapping theorem; Krasnoselskii’s fixed point theorem; boundary value problem; the half line 1008-1542(2016)06-0562-13 10.7535/hbkd.2016yx06007 2016-03-24; 2016-09-10;责任编辑:张 军 河北省自然科学基金(A2013208108) 江卫华(1964—),女,河北邯郸人,教授,博士,主要从事应用泛函分析、常微分方程边值问题方面的研究。 E-mail:jianghua64@163.com O175.8 MSC(2010)主题分类:34B18 A 江卫华,李庆敏,周彩莲.分数阶脉冲微分方程边值问题解的存在性[J].河北科技大学学报,2016,37(6):562-574. JIANG Weihua, LI Qingmin, ZHOU Cailian.Existence of solutions to boundary value problem of fractional differential equations with impulsive[J].Journal of Hebei University of Science and Technology,2016,37(6):562-574.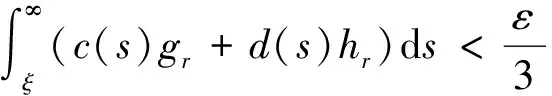
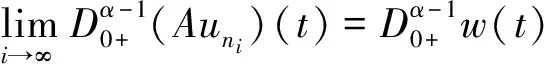
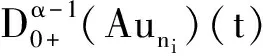
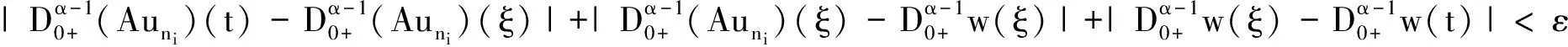
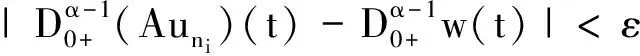
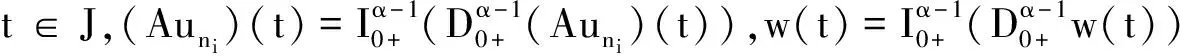
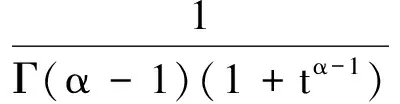

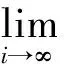
4 举 例