一类Caputo分数阶微分方程正解的存在性
李云红,吕文静
(1.河北科技大学理学院,河北石家庄 050018;2.河北科技大学总务处,河北石家庄 050018)
一类Caputo分数阶微分方程正解的存在性
李云红1,吕文静2
(1.河北科技大学理学院,河北石家庄 050018;2.河北科技大学总务处,河北石家庄 050018)
为了研究一类带p-Laplacian 算子的Caputo分数阶微分方程边值问题正解的存在性,通过计算得到该问题的格林函数,并讨论其性质。运用单调迭代方法,得到该边值问题至少存在2个正解,最后通过实例验证了此类方程边值问题正解的存在性。
常微分方程其他学科;Caputo分数阶微分;正解;单调迭代方法;边值问题
微分方程是现代数学的一个重要分支,它在几何、力学、航天、经济等领域都有着广泛的应用。近年来,分数阶微分方程边值问题成为许多数学工作者的研究热点[1-14]。
本文讨论带p-Laplacian算子的边值问题的正解情况,

在本文中,总假设下面条件成立:
H1)μ1>0,μ2>0,0<η<1,ρ=η+μ1-μ2,ρ>0,(α-1)μ2≥1;
H2)f:[0,1]×[0,+∞)→[0,+∞)是连续的;

1 预备知识
为证明结论,需要利用下面的预备知识[15-16]。
定义1 函数y:(0,+∞)→R的α>0阶Riemann-Liouville积分定义如下:
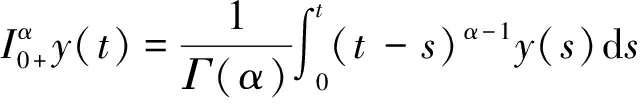
其中右边是在(0,+∞)上逐点定义的。
定义2 函数y:(0,+∞)→R的α>0阶Caputo微分定义如下:
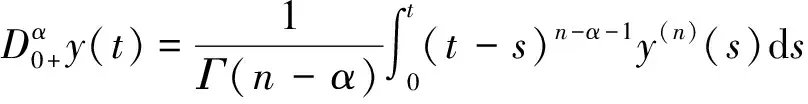
其中n=[α]+1,右边是在(0,+∞)上逐点定义的。
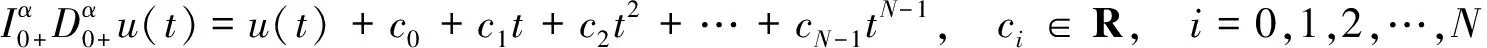
其中N是大于或等于α的最小整数。
2 主要结果
引理2 边值问题(1)等价于
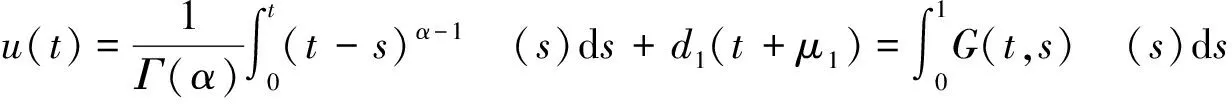
(2)
其中:
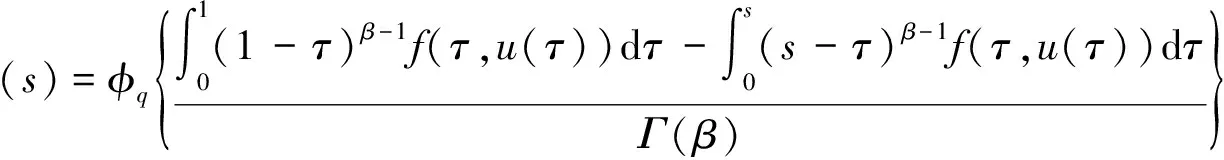
(3)
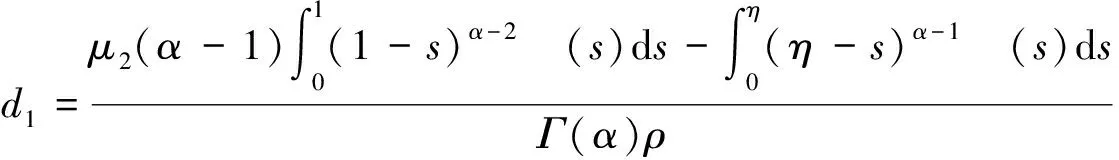
(4)
(5)
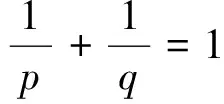
两边从0到t积分,利用引理1得
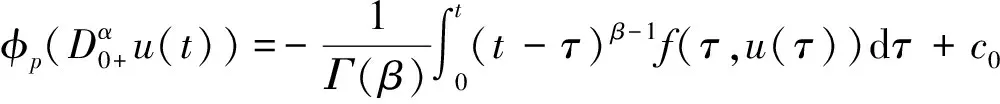
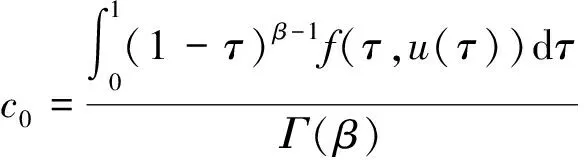
因此,
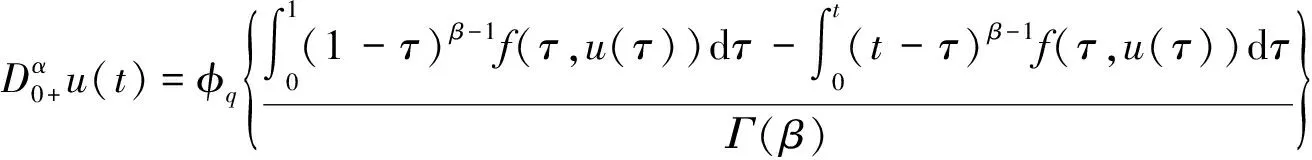
对上式两边从0到t积分,利用引理1得
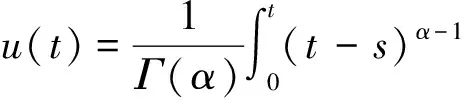
利用式(1)中的u″(0)=0,得d2=0,所以
(6)
由式(6),可得
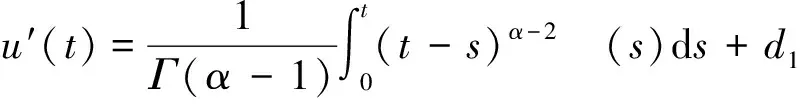
(7)
由式(6)、式(7)和式(1)中的u(0)=μ1μ′(0),可得
d0=μ1d1。
(8)
由式(6)—式(8)和式(1)中的u(η)=μ2u′(1),可得
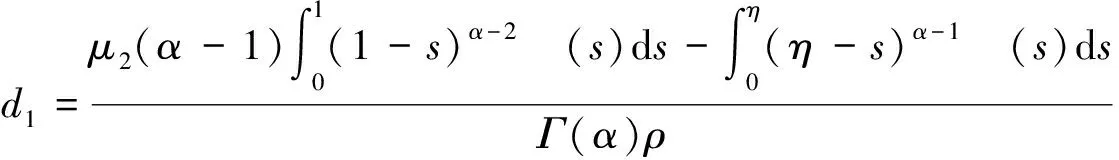
证明完毕。
引理3 引理2中的ϖ(s)≥0,对于0≤s≤t≤1。d1≥0。G(t,s)≥0且k1p(s)≤G(t,s)≤k2p(s),
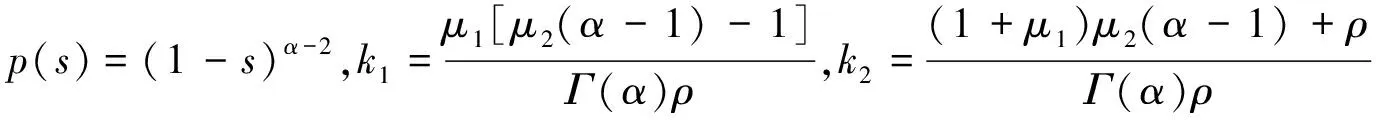
证明 由条件H2)可得f(t,u(t))≥0,因此对任意的0≤s≤t≤1,有:
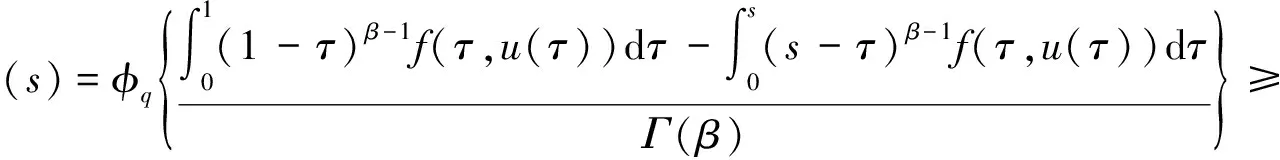
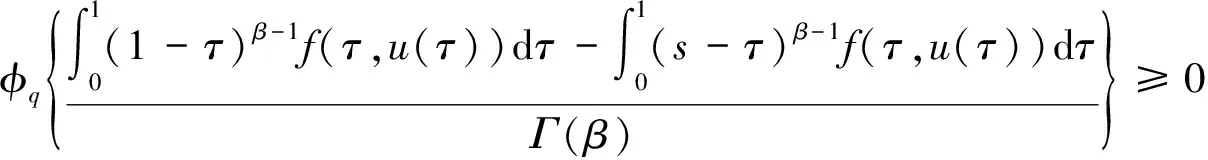
由条件H1)可得μ2>0,0<η<1,ρ=η+μ1-μ2>0,(α-1)μ2≥1,因此
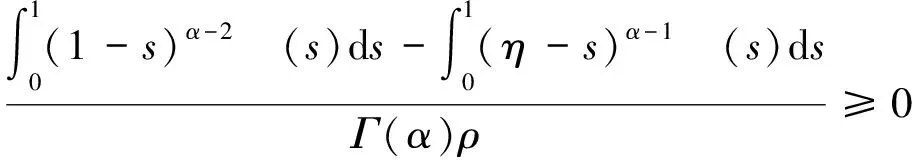
当0≤s≤min{t,η}≤1时,

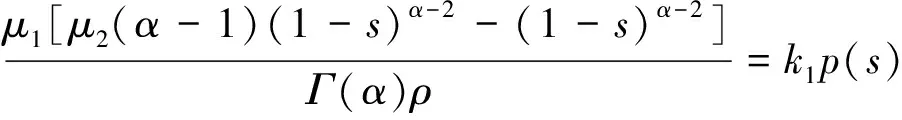
所以k1p(s)≤G(t,s)≤k2p(s)。又因为(α-1)μ2≥1,所以k1≥0,因此G(t,s)≥0。其他区间的证明类似,省略。
K={u|u∈E,u是[0,1]上的非负,不减的函数}。
算子T:K→E为
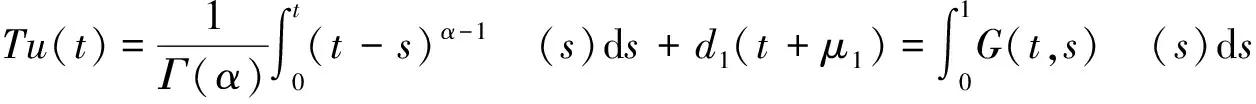
(9)
定理1 设条件H1)—H3)成立,且存在常数r>1,使得
S1) 当0≤t≤1,0≤u≤v≤r时,有f(t,u)≤f(t,v);

则边值问题(1)至少存在2个正解u*和v*,使得0≤‖u*‖≤r,0≤‖v*‖≤r,其中:
证明 首先证明T:K→K是全连续的。
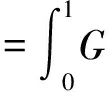
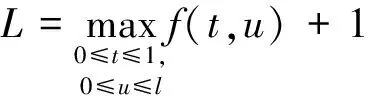
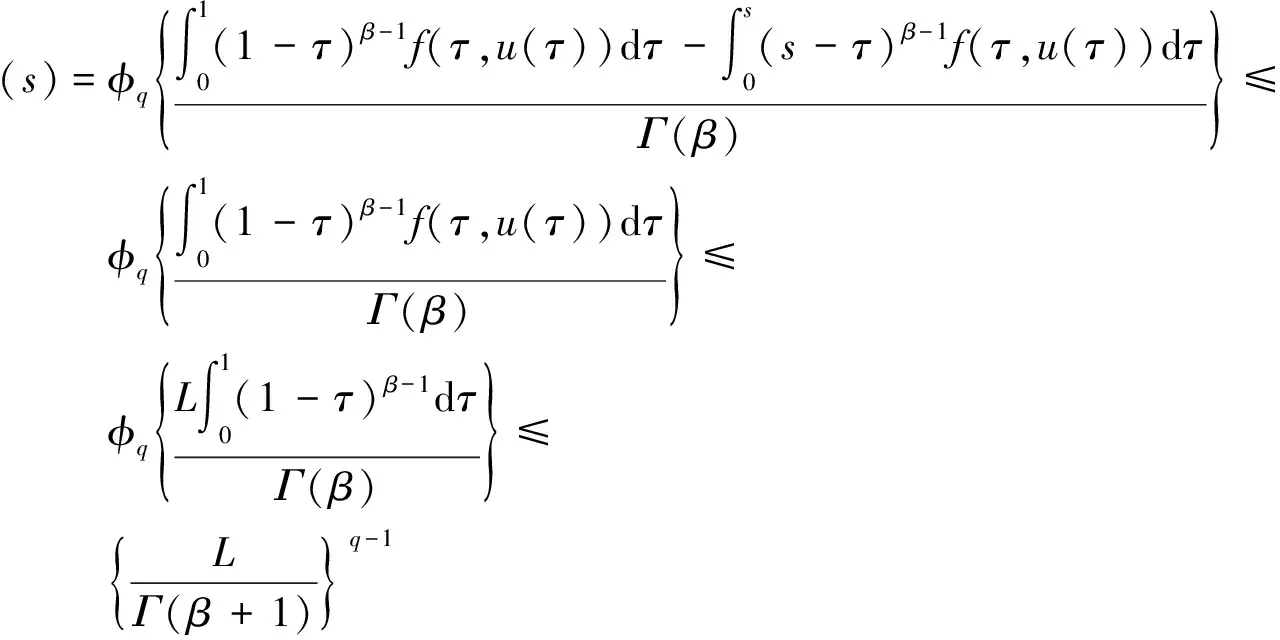
因此,
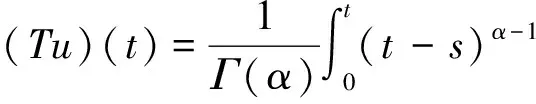
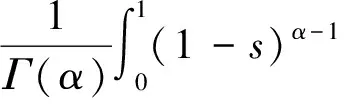
所以T(M)是一致有界的。
下面来证明T(M)是等度连续的。任取u∈M,0≤t1≤t2≤1,可得
|(Tu)(t2)-(Tu)(t1)|≤
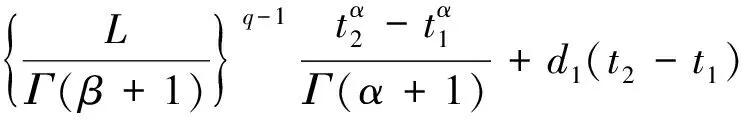
这样T(M)是等度连续的,应用Arzel-Ascoli定理,可得T是全连续的。
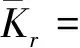
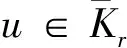
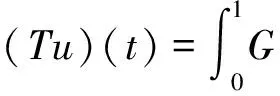
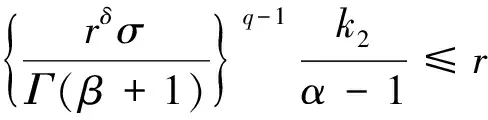
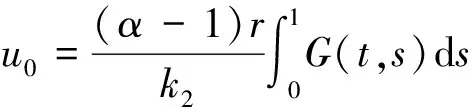
因为
u1(t)=(Tu0)(t)=
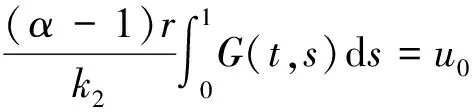
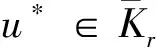
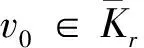
注:定理1中的u*,v*有可能重合,在这种情况下问题(1)至少有1个正解。
3 举 例
讨论下面边值问题的正解情况,
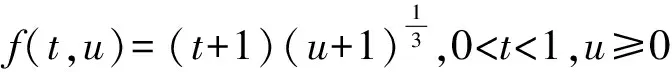
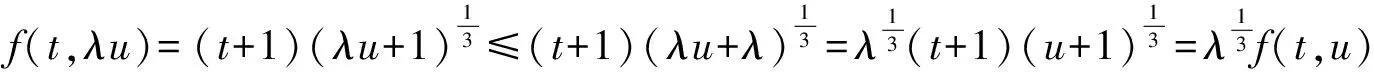
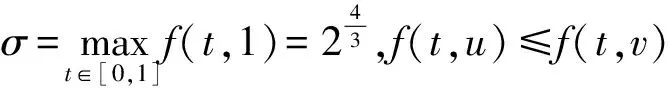

利用定理1可知,上述边值问题至少有2个正解。
[1] AHMAD B, MATAR M, AGARWAL R. Existence results for fractional differential equations of arbitrary order with nonlocal integral boundary conditions[J]. Boundary Value Problem,2015,220:1-13.
[2] ZHANG Lihong, AHMAD B, WANG Guotao,et al. Nonlinear fractional integro-differential equations on unbounded domains in a Banach space[J]. Journal of Computational and Applied Mathematics,2013,240:51-56.
[3] ALBERTO C, HAMDI Z. Nonlinear fractional differential equations with integral boundary value conditions[J]. Applied Mathematics and Computation,2014,228:251-257.
[4] VONG S. Positive solutions of singlular fractional differential equations with integral boundary conditions[J]. Mathematical and Computer Modelling,2013,57: 1053-1059.
[5] SOTIRIS K N, SINA E. On the existence of solutions for fractional differential inclusions with sum and integral boundary conditions[J]. Applied Mathematics and Computation,2015,266: 235-243.
[6] KOU Chunhai, ZHOU Huacheng, YAN Ye. Existence of solutions of initial value problems for nonlinear fractional differential equations on the half-axis[J]. Nonlinear Analysis,2011,74: 5975-5986.
[7] CUI Yujun. Uniqueness of solution for boundary value problems for fractional differential equations[J]. Applied Mathematics Letters,2016,51:48-54.
[8] ZHANG Lihong,AHMAD B, WANG Guotao. The existence of an extremal solution to a nonlinear system with the right-handed Riemann-Liouville fractional derivative[J]. Applied Mathematics Letters,2014,31:1-6.
[9] LI Yunhong, LI Guogang. Positive solutions ofp-Laplacian fractional differential equations with integral boundary value conditions[J]. Journal of Nonlinear Science and Applications,2016,9(3):717-726.
[10]ZHAI Chengbo, XU Li. Properties of positive solutions to a class of four-point boundary value problem of Caputo fractional differential equations with a parameter[J]. Communications in Nonlinear Science Numerical Simulation,2014,19:2820-2827.
[11] XU Xiaojie,FEI Xiangli. The positive properties of Green’s function for three point boundary value problems of nonlinear fractional differential equations and its applications[J]. Communications in Nonlinear Science Numerical Simulation,2012,17(4):1555-1565.
[12] NTOUYAS S, ETEMAD S. On the existence of solutions for fractional differential inclusions with sum and integral boundary conditions[J]. Applied Mathematics and Computation,2015,266:235-243.
[13] 李云红,李艳. 带p-Laplacian算子的分数阶微分方程的正解[J].河北科技大学学报,2015,36(6):593-597. LI Yunhong,LI Yan. A positive solution for the fractional differential equation with ap-Laplacian operator[J]. Journal of Hebei University of Science and Technology, 2015,36(6):593-597.
[14] ZHANG Xinguang, LIU Lisan, WIWATANAPATAPHEE B, et al. The eigenvalue for a class of singularp-Laplacian fractional differential equations involving the Riemann-Stieltjes integral boundary condition[J]. Applied Mathematics and Computation,2014,235:412-422.
[15]AMKO S G,KILBAS A A,MARICHEV O I. Fractional Integrals and Derivatives: Theory and Applications[M]. Switzerland: Gordon and Breach,1993.
[16]PODLUNY I. Fractional Differential Equations, Mathematics in Science and Engineering[M]. New York: Academic Press,1999.
Existence of positive solutions to a class of Caputo fractional differential equations
LI Yunhong1, LYU Wenjing2
(1.School of Science, Hebei University of Science and Technology, Shijiazhuang, Hebei 050018, China;2. Office of General Services, Hebei University of Science and Technology, Shijiazhuang, Hebei 050018, China)
In order to investigate the existence of positive solutions to a class of Caputo fractional differential equation boundary value problems withp-Laplacian operator, the Green’s function is obtained by calculus, and its properties are discussed. By using monotone iterative technique, at least two positive solutions are obtained for the boundary value problems. An example is given to illustrate the existence of positive solutions to this kind of equation boundary value problems.
ordinary differential equation; Caputo fractional derivative;positive solution;monotone iteratiation;boundary value problems
1008-1542(2016)06-0575-06
10.7535/hbkd.2016yx06008
2016-05-23;
2016-10-19;责任编辑:张 军
国家自然科学基金(11401159);河北省自然科学基金(A2014208158)
李云红(1978—),女,河北鹿泉人,讲师,硕士,主要从事微分方程方面的研究。
E-mail:mathhong@126.com
O175.1 MSC(2010)主题分类:34B15
A
李云红,吕文静.一类Caputo分数阶微分方程正解的存在性[J].河北科技大学学报,2016,37(6):575-580. LI Yunhong,LYU Wenjing. Existence of positive solutions to a class of Caputo fractional differential equations[J].Journal of Hebei University of Science and Technology,2016,37(6):575-580.

