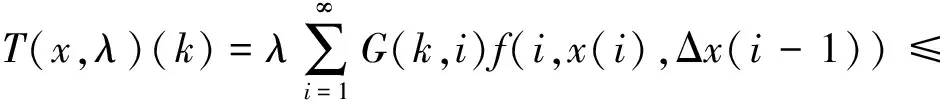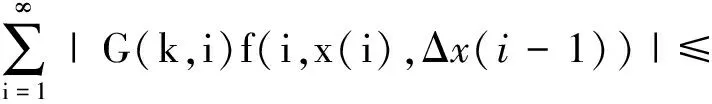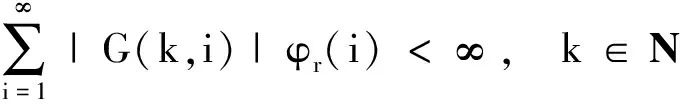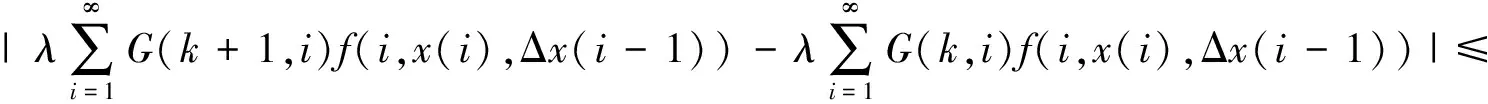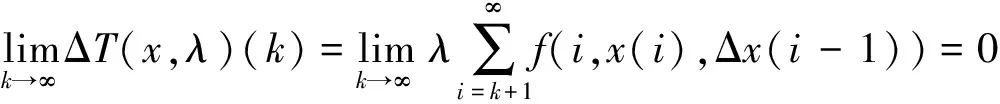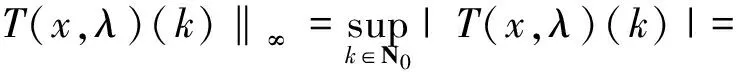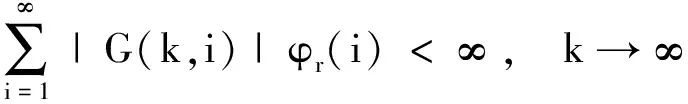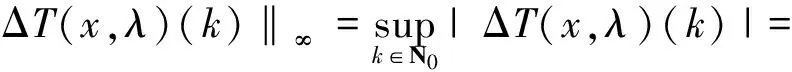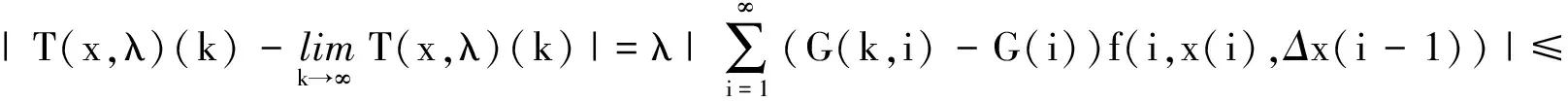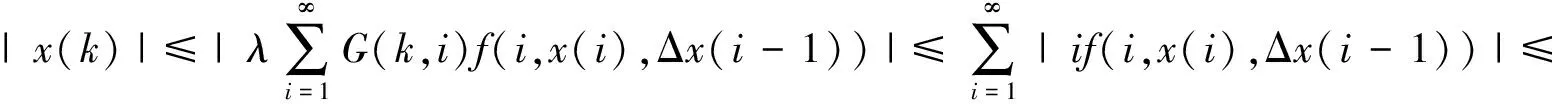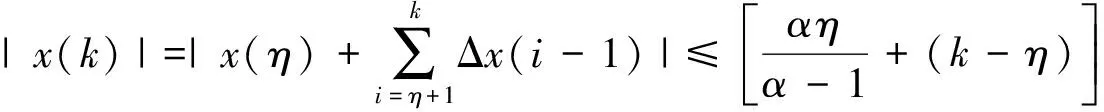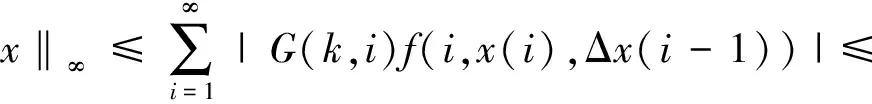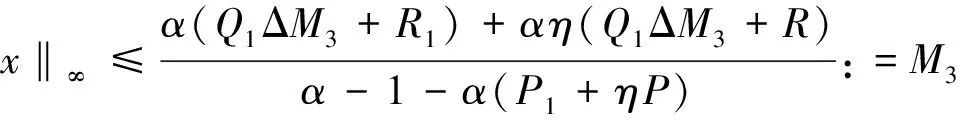无穷区间上二阶三点差分方程边值问题正解的存在性

郭彦平，苗素荣，禹长龙

(河北科技大学理学院，河北石家庄 050018)



无穷区间上二阶三点差分方程边值问题正解的存在性

郭彦平，苗素荣，禹长龙

(河北科技大学理学院，河北石家庄 050018)

为了将差分方程应用到解无穷区间边值问题，借助于相应线性边值问题Green函数的性质，研究了无穷区间上的二阶三点差分方程边值问题。通过Banach压缩映像原理和Leray-Schauder不动点定理获得了该问题正解的存在性和唯一性定理，推广了已有结论。

常微分方程其他学科；差分方程；Green 函数；Leray-Schauder不动点定理；无穷区间

无穷区间边值问题起源于应用数学和物理领域，具有广泛的应用背景[1-2]。近年来，由于无穷区间边值问题的广泛应用，引起了学者的关注，尤其是在利用各种不动点理论、拓扑度理论、重合度理论以及上下解方法等非线性泛函的工具对无穷区间上的2阶、n阶等边值问题(Dirichlet问题、周期、脉冲、时滞等边值问题)的研究中获得了重要研究成果，参见文献[3—10]。

随着现代科学技术的进步，许多生产实际和科学研究中所遇到的微分方程极其复杂，很多情况下很难得到解甚至根本得不到解析表达式。为解决问题，自然需要考虑其近似解或研究解的性质，这就需要将微分方程离散化，这便得到了差分方程。由于差分方程在现代医学、生物数学、生态学、物理学、化学等方面的广泛应用，已有很多学者利用各种方法和技巧对差分方程边值问题进行了研究，但是相对微分方程边值问题则缺乏足够的理论和方法。

对无穷区间上的差分方程边值问题的研究已有一些成果[11-18]，但整体上，无穷区间上的差分方程边值问题的结果尚少，理论尚不完善，还需要更多的研究和讨论。

在文献[19]中，AGARWAL等研究了无穷区间上的二阶差分方程边值问题：

非负解的存在性。

在文献[20]中，LIAN等利用Schauder不动点定理和上下解的技术研究了无穷区间上的二阶差分方程边值问题:

-Δ2xk-1=f(k,xk,Δxk-1),k∈N,

x0-aΔx0=B, Δx∞=C

1个和3个无界解的存在性。

在本文中，运用Leray-Schauder不动点定理研究无穷区间上的二阶差分方程三点边值问题:

(1)

解的存在性，其中N={1,2,…,∞}，f:N×R2→R是连续函数，α∈R,α≠1，η∈N且Δx(k)=x(k+1)-x(k)。

C1)f:N×R2→R是连续函数，且∀r>0，∀k∈N；∃φr(k)，kφr(k)∈l1，φr(k)>0；使得当max{|u|,|v|}≤r时，∀k∈N有|f(k,u,v)|≤φr(k)；

C2)f:N×R2→R是连续函数，且∃p(k),q(k),r(k)∈l1；且kp(k),kq(k),kr(k)∈l1，使得∀k∈N,(u,v)∈R2有|f(k,u,v)|≤p(k)|u|+q(k)|v|+r(k)。

1 预备知识

引理1 若{v(k)}k∈N和{kv(k)}k∈N∈l1，则线性边值问题：

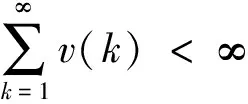
由x(k)=αx(η)和式(4)可得：

,

命题得证。

附注1 显然G(k,i)满足Green函数的性质，所以称G(k,i)为无穷区间三点边值问题(2)对应的齐次方程的Green函数。

引理2 ∀k,i∈N，则

证明 对于∀i∈N，G(k,i)关于k为非减函数。于是有

故而有

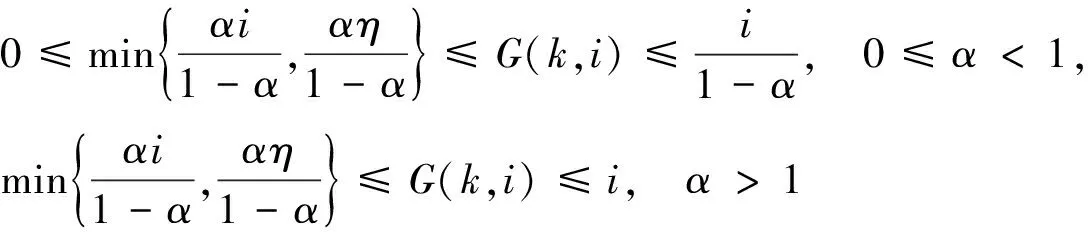
因此命题得证。

引理3Green函数G(k,i)满足：

2 主要结论

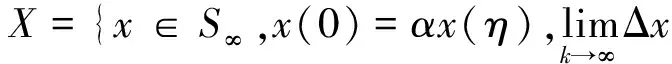
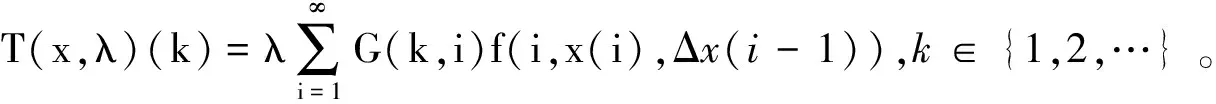
引理4 设条件C1)成立，则∀λ∈[0,1]，T(x,λ)在X上是全连续的。

证明 首先，证明Tx∈X。对∀x∈X，则∃r>0,使得‖x‖

由T的定义得：

|Δ(T(x,λ)(k))|= |(T(x,λ)(k+1)-T(x,λ)(k))|=

其次，证明T(x,λ)在X连续。设∀xn∈X,当n→∞时，xn→x。下面证明∀λ∈[0,1],当n→∞时，T(xn,λ)→T(x,λ)。由条件C1)知

其中r0>0是一实数。且maxn∈N{‖xn‖,‖x‖}≤r0，于是有

|T(xn,λ) (k)-T(x,λ)(k)|≤

且

|ΔT(xn,λ) (k)-ΔT(x,λ)(k)|≤

因此，T是连续的。

最后，证明T是紧的，即T映X中的有界集为相对紧集。设B⊂X为有界子集，则∃r>0,∀x∈B,‖x‖

且

因此，TB是有界的。又

且

|ΔT(x,λ)(k)|≤

因此，TB在无穷远处一致收敛，故TB为相对紧的。由定理1知，T(·,λ):X×[0,1]→X是全连续的。

证明 由引理1，显然当且仅当x是T(·,λ)的不动点时，x∈X是边值问题(1)的解。显然，∀x∈X有T(x,0)=0。由Leray-Schauder连续定理可知定理的证明只需证明∀λ∈[0,1]，T(·,λ)在闭集X中的不动点不依赖于λ即可。

下面证明T(·,λ)的不动点有一个不依赖λ的先验界M。假设x=T(x,λ)且记

情形1α<0，∀x∈X,∀k∈N有

因此，

‖Δx‖∞≤ ‖λf(i,x(i),Δx(i-1))‖l1≤‖f(i,x(i),Δx(i-1))‖l1≤

‖p(i)|x(i)|+q(i)|Δx(i-1)|+r(i)‖l1≤(ηP+P1+Q)‖Δx‖∞+R,

即

同理，得：

P1‖x‖∞+Q1ΔM1+R1,k∈N,

即

记M=max{M1,ΔM1},M与λ无关,则‖x‖≤M。

情形2 0≤α<1，对任意∀x∈X,∀k∈N有

记M=max{M2,ΔM2},M与λ无关，则‖x‖≤M。

情形3α>1，对于∀x∈X，∀k∈N，得：

同理，有：

且

即

记M=max{M3,ΔM3},与λ无关。所以边值问题(1)至少有1个解。

[1] 郑连存，张欣欣，赫冀成. 传输过程奇异非线性边值问题[M]. 北京：科学出版社，2003.

[2] KIDDER R E. Unsteady flow of gas through a semi-infinite porous medium[J]. Journal of Applied Mechanics,1957,24:329-332.

[3] AGARWAL R P, O’REGAN D. Infinite Interval Problems for Differential,Difference and Integal Equations[M]. London：Kluwer Academic Publisher, 2001.

[4] O'REGAN D. Theory of Singular Boundary Value Problems[M].New Jersey:World Scientific,1994.

[5] AGARWAL R P, O’REGAN D. Nonlinear boundary value problems on the semi-infinite interval: An upper andlower solution approach[J]. Mathematika, 2002,49(1): 129-140.

[6] BAXLEY J V. Existence and uniqueness for nonlinear boundary value problems on infinite interval[J]. Journal of Mathematical Analysis and Applications, 1990,147(1): 122-133.

[7] 禹长龙，王菊芳，李国刚. 无穷区间上含有p-Laplacian算子的n阶积分边值问题正解的存在性[J]. 河北科技大学学报，2015,36(4)：382-389. YU Changlong, WANG Jufang, LI Guogang. Existence of position solutions fornth-order integral boundary value problems withp-Laplacian operator on infinite interval[J]. Journal of Hebei University of Science and Technology, 2015,36(4)：382-389.

[8] AHMAD B, ALSAEDI A, ALGHAMDI B S. Analytic approximation of solutions of the forced duffing equation with integral boundary conditions[J]. Nonlinear Analysis: Real World Applications, 2008,9(4): 1727-1740.

[9] LIAN H, GE W. Solvability for second-order three-point boundary value problems on a half-line[J]. Applied Mathematics Letters, 2006, 19(10): 1000-1006.

[10]GUO Yanping, YU Changlong, WANG Jufang. Existence of three positive solutions for m-point boundary value problems on infinite intervals[J]. Nonlinear Analysis:Theory,Method & Applications, 2009,71: 717-722.

[11]AGARWAL R P, BOHNER M, O’REGAN D. Time scale boundary value problems on infinite intervals[J]. Journal of Computational & Applied Mathematics,2002,141: 27-34.

[12]AGARWAL R P, O’REGAN D. Boundary value problems for general discrete systems on infinite intervals[J].Computers & Mathematics with Applications,1997,33(7): 85-99.

[13]AGARWAL R P, O’REGAN D. Existence and approximation of solutions of nonlinear discrete systems on infinite intervals[J]. Mathematical Methods in the Applied Sciences, 1999,22(1): 91-99.

[14]AGARWAL R P, O’REGAN D. Continuous and discrete boundary value problems on the infinite interval: Existence theory[J].Mathematika, 2001,48(1/2): 273-292.

[15]AGARWAL R P, O’REGAN D. Nonlinear urysohn discrete equations on the infinite interval:A fixed point approach [J]. Computers & Mathematics with Applications, 2001，42(3/4/5):273-281.

[16]GUSEINOV G S. A boundary value problem for second order nonlinear difference equations on the semi-infinite interval[J]. Journal of Difference Equations & Applications, 2002,8(8): 1019-1032.

[17]TIAN Yu, GE Weigao. Multiple positive solutions of boundary value problems for second order discrete equations on the half-line[J]. Journal of Difference Equations & Applications, 2006,12(12):191-208.

[18]TIAN Yu, TISDELL C C, GE Weigao, The method of upper and lower solutions for discrete BVP on infinite intervals[J]. Journal of Difference Equations & Applications, 2011,17(3): 267-278.

[19]AGARWAL R P, O'REGAN D. Discrete systems on infinite intervals[J]. Computers & Mathematics with Applications, 1998,35(9): 97-105.

[20]LIAN Hairong, LI Jingwu, AGARWAL R P. Unbounded solutions of second order discrete BVPs on infinite intervals[J]. Journal of Nonlinear Science and Applications, 2016, 9(2):357-369.

Existence of positive solutions to boundary value problem of second-order three-point difference equations on infinite intervals

GUO Yanping, MIAO Surong, YU Changlong

(School of Science, Hebei University of Science and Technology, Shijiazhuang, Hebei 050018, China)

In order to apply difference equation in boundary value problem on infinite intervals, with the help of the properties of Green function in linear boundary value problems，the boundary value problem of second-order three-point difference equations on infinite intervals is studied. The theory of existence and uniqueness of positive solutions to this problem is are obtained by Banach's contraction mapping principle and Leray-Schauder fixed point theorem, which generalizes the known results.

ordinary differential equation； difference equation； Green function； Leray-Schauder fixed point theorem； infinite interval

1008-1542(2016)06-0556-06

10.7535/hbkd.2016yx06006

2016-05-12；

2016-09-06；责任编辑：张 军

国家自然科学基金(11201112)；河北省自然科学基金(A2013208147, A2014208152, A2015208114)；河北省高等学校科学技术研究项目(QN2015175，QN2016165)

郭彦平(1965—)，男，河北张家口人，教授，博士，主要从事微分方程边值问题方面的研究。

E-mail： guoyanping65@sohu.com

O175 MSC(2010)主题分类:34B40

A

郭彦平，苗素荣，禹长龙.无穷区间上二阶三点差分方程边值问题正解的存在性 [J].河北科技大学学报,2016,37(6):556-561. GUO Yanping, MIAO Surong, YU Changlong.Existence of positive solutions to boundary value problem of second-order three-point difference equations on infinite intervals[J].Journal of Hebei University of Science and Technology,2016,37(6):556-561.