图的ABC指标与直径
武 琳,胡玉梅
(天津大学理学院,天津 300350)
图的ABC指标与直径
武 琳,胡玉梅
(天津大学理学院,天津 300350)
为了更好地研究拓扑指标在物理化学领域的良好性质,考虑基于度和基于距离的指标之间的关系问题,在直径这一作为距离的不变量的基础上,研究了图的ABC指标和直径的关系。根据相关引理,推导出了树和单圈图的ABC指标与直径的关系,得出了ABC指标和直径差值的紧的下界。
代数拓扑;ABC指标;直径;树;单圈图;极值
拓扑指标在物理化学领域有着广泛的应用价值和深远的研究意义[1-9]。随着图论理论的不断发展和完善,拓扑指标主要分为2类:基于度的指标和基于距离的指标。ABC指标是一个基于度的拓扑指标,它由ESTRADA等[10]提出,相关性质的研究见文献[11—17],图G的ABC指标的定义式为


1 树的ABC指标与直径
引理1 设x1x2是图G中的悬挂边,则ABC(G)-ABC(G-x1x2)>0。
证明
ABC(G)-ABC(G-x1x2)=



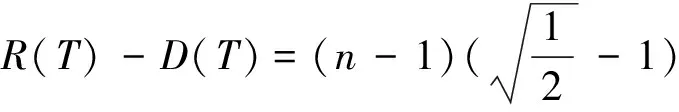
假设T不是路,故T至少有3个悬挂边。若P=v0v1…vD是T的直径路,则V(P)=D+1,E(P)=D,D(P)=D(T)=D。令u1,u2,…,um是不在直径路P上的悬挂点,则有:

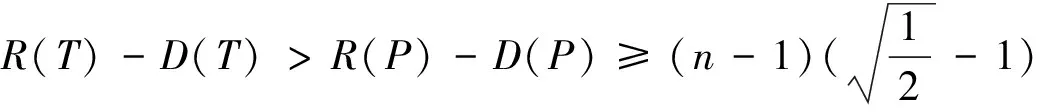
2 单圈图的ABC指标与直径
引理2 设G是一个不同构于Cn的单圈图,n≥7,n1≤(n-3),v是G的直径路P上的叶子点,u是v的邻点。若N(u)中仅有一个顶点的度数不小于2,则有:
当D(G-v)=D(G)时,ABC(G)-ABC(G-v)>0;

证明 令N(u)-{v}={x1,x2,…,xd(u)-1},不妨设x1是度数不小于2的顶点。
当D(G-v)=D(G)时,显然有d(u)≥3,此时,
ABC(G)-ABC(G-v)=

当D(G-v)=D(G)-1时,显然有d(u)=2。设w是u的邻点,d(w)≥2,则有:
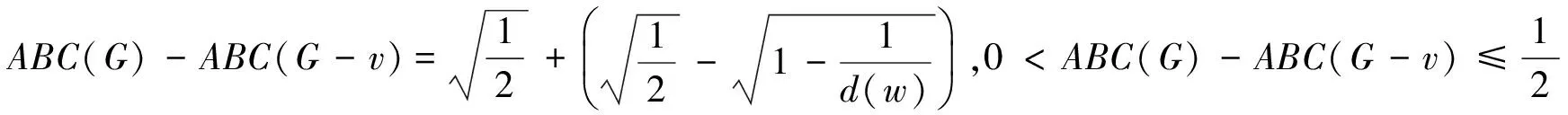

证明 情况1N(u)仅有一个顶点的度至少是2,对n用数学归纳法,


情况2N(u)中有2个顶点的度数不小于2,
当D(G-v)=D(G)时,
若G仅有1个叶子点v,与D(G-v)=D(G)矛盾;
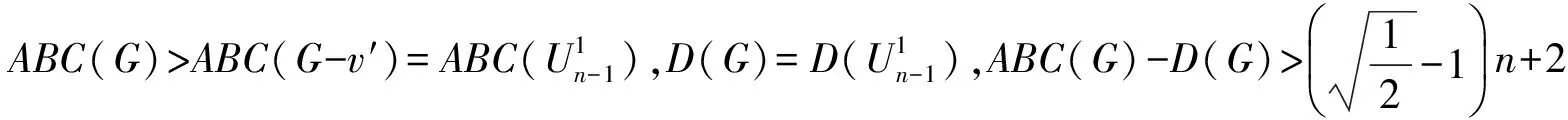
若G有多于2个叶子点,依次删除不在直径路上的叶子点,得到图G′,则



[1] RANDIC M. Characterization of molecular branching[J]. Journal of the American Chemical Society, 1975, 97(23): 6609-6615.
[2] ROUVRAY H D. Predicting chemistry from topology[J]. Scientific American, 1986, 255:40-47.
[3] ROUVRAY H D. The modeling of chemical phenomena using topological indices[J]. Journal of Computational Chemistry, 1987, 8(4):470-480.
[4] WIENER H. Structural determination of paraffin boiling points[J]. Journal of the American Chemical Society, 1947, 69(1):17-20.
[5] ZHOU B, TRINAJSTIC N. On a novel connectivity index[J]. Journal of Mathematical Chemistry, 2009, 46(4):1252-1270.
[6] ZHOU B, TRINAJSTIC N. On general sum-connectivity index[J]. Journal of Mathematical Chemistry, 2010, 47(1):210-218.
[7] GAO J, LU M. On the randic index of unicyclic graphs[J]. Match Communications in Mathematical & in Computer Chemistry, 2005, 53(2):377-384.
[8] GUTMAN I, POTGIETER H J. Wiener index and intermolecular forces[J]. South African Journal of Science, 1996, 92(3):47-48.
[9] BOLLOBAAS B, ERDOS P. Graphs of extremal weights[J]. Ars Combinatoria,1998,50:225-233.
[10]ESTRADA E, TORRES L, RODRIGUEZ L, et al . An atom-bond connectivity index: Modelling the enthalpy of formation of alkanes[J]. Indian Journal of Chemistry, 1998, 37(10):849-855.
[11]ESTRADA E. Atom-bond connectivity and the energetic of branched alkanes[J]. Chemical Physics Letters, 2008, 463(4/5/6):422-425.
[12]DAS C K. Atom-bond connectivity index of graphs[J]. Discrete Applied Mathematics, 2010, 158(11):1181-1188.
[13]FURTULA B, GRAOVAC A, VUKICEVIC D.Atom-bond connectivity index of trees[J]. Discrete Applied Mathematics, 2009, 175: 2828-2835.
[14]GUTMAN I, FURTULA B. Trees with smallest atom-bond connectivity index[J]. Match Communications in Mathematical & in Computer Chemistry, 2012, 68(1):131-136.
[15]GUTMAN I, FURTULA B, IVANOVIC M. Notes on trees with minimal atom-bond connectivity index[J]. Match Communications in Mathematical & in Computer Chemistry, 2012, 67(3):467-482.
[16]HOSSEINI A S, AHMADI B M, GUTMAN I. Kragujevac trees with minimal atom-bond connectivity index[J]. MATCH Commun Math Comput Chem, 2014, 71(20): 5-20.
[17]ZHOU B, XING R. On atom-bond connectivity index[J]. Zeitschrift Fur Naturforschung A, 2011, 66(1/2):61-66.
[18]CHEN L, LI X, LIU M, et al. On a relation between szeged and wiener indices of bipartite graphs[J]. Transactions on Combinatorics, 2012, 1(4):43-49.
[19]HOROLDAGVA B,DAS K C. On comparing Zagreb indices of graphs[J]. Hacettepe University Bulletin of Natural Sciences and Engineering,2012,41(4):223-230.
[20]HOROLDAGVA B, GUTMAN I. On some vertex-degree-based graph invariants[J]. Match Communications in Mathematical & in Computer Chemistry, 2011, 65(3):723-730.
[21]LIU Jianxi. On harmonic index and diameter of graphs[J]. Journal of Appied Mathematics and Physics, 2013,1(3):5-6.
Atom-bond connectivity index and diameter of graphs
WU Lin, HU Yumei
(School of Science, Tianjin University, Tianjin 300350, China)
For further study of the numerous nice properties of topological indices in physical and chemical fields, it is worth considering the relation between a degree-based index and a distance-based index. With the fact that diameter is an invariant based on distance, the relations between atom-bond connectivity index, diameter in trees and unicyclic graphs are studied. Based on relative lemma, the relation between atom-bond connectivity index and diameter in tree and unicyclic graphs is investigated, then the sharp lower bounds of the difference of index and diameter are given.
algebraic topology;ABCindex; diameter; tree; unicyclic graph; extreme value
1008-1542(2016)06-0552-04
10.7535/hbkd.2016yx06005
2016-03-29;
2016-09-29;责任编辑:张 军
国家自然科学基金(11001196)
武 琳(1992-),女,天津人,硕士研究生,主要从事图论与组合最优化方面的研究。
胡玉梅副教授。E-mail:huyumei@tju.edu.cn
O157 MSC(2010)主题分类:55-04
A
武 琳,胡玉梅.图的ABC指标与直径[J].河北科技大学学报,2016,37(6):552-555. WU Lin, HU Yumei .Atom-bond connectivity index and diameter of graphs[J].Journal of Hebei University of Science and Technology,2016,37(6):552-555.

