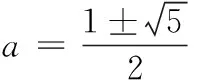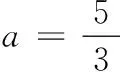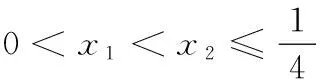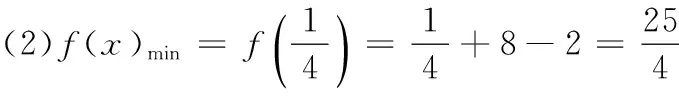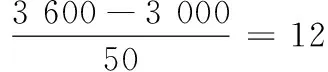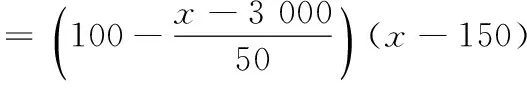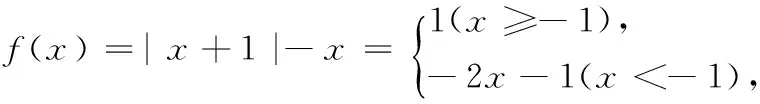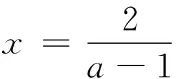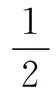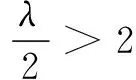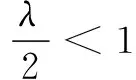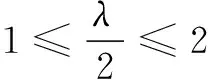高一数学测试



○课外测试○

高一数学测试

一、填空题(本大题共14小题，每小题5分，共70分)

2.已知f(x)=2x+3,函数g(x)=3x-5,则 f(g(x))=______.

3.已知函数f(x)=x2+mx+1是偶函数,则m=______.

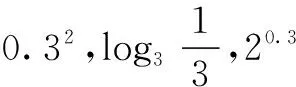
5.函数f(x)=x2-2x-1, x∈[-1,2]的单调增区间为______.

6.已知函数y=f(x)在定义域[-2,4]上是单调减函数,且f(a+1)>f(2a),则a的取值范围为______.

7.若a>0,b>0, 则

可化简为______.

9.方程e2x+1=ex2-2的根为______.

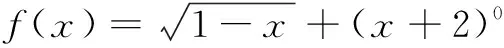
11.关于x的方程7x+1-7x·a-a-5=0有负根,则实数a的取值范围是______.

当x∈[0,1)时,

则 f(9.9)=______.

二、解答题(本大题共6小题,计90分.解答应写出必要的文字说明、证明过程或演算步骤)

(1)若A∩B=A∪B,求a的值;

16.(本小题满分14分)已知函数f(x)=-x2+2ax+1-a在区间[0,2]上的最大值为2,求实数a的值.

17.(本小题满分15分)已知函数

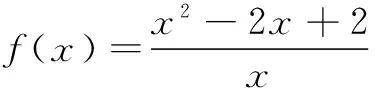
18.(本小题满分15分)某租赁公司拥有汽车100辆,每辆车的月租金为3 000元时,可全部租出.每辆车的月租金每增加50元,未租出的车将会增加一辆，租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.

(1)当每辆车的月租金定为3 600元时,能租出多少辆车?

(2)当每辆车的月租金为多少元时,租赁公司的月收益最大?最大月收益是多少?

19.(本小题满分16分)已知函数

f(x)=|x+1|+ax(a∈R).

(1)a=-1时,画出f(x)的图象,并求其值域;

(2)若函数f (x)在R上具有单调性,求a的取值范围.

20.(本小题满分16分)已知函数f(x)=3x的定义域为R,满足f(a+2)=18,函数g(x)=λ·3ax-4x的定义域为[0,1].

(1)求实数a的值;

(2)若函数g(x)为单调减函数,求实数λ的取值范围;

参考答案

一、填空题

1.{6}； 2.6x-7; 3.0;

6.1

9.-1或3; 10.{x|x≤1,且x≠-2};

=f(x-1),

∴f(x+2)=f(x),

二、解答题

15.由已知,得B={2,3},C={2,-4}.

(1)∵A∩B=A∪B,∴A=B,于是2,3是一元二次方程x2-ax+a2-19=0的两个根.

由韦达定理,知

解之得a=5.

又A∩C=∅，得3∈A,2∉A,-4∉A.

由3∈A,得32-3a+a2-19=0,解得a=5或a=-2.

当a=5时，A={x|x2-5x+6=0}={2,3},与2∉A矛盾；

当a=-2时，A={x|x2+2x-15=0}={3,-5},符合题意，

∴a=-2.

16.f(x)=-x2+2ax+1-a =-(x-a)2+a2+1-a.

当a<0时，f(x)max=f(0)=1-a=2,∴a=1;

f(x2)-f(x1)

∴f(x2)-f(x1)<0,

∴f(x2)

18.(1)当每辆车的月租金定为3 600元时,未租出的车辆数为

100-12=88(辆).

答:这时租出了88辆车.

(2)设每辆车的月租金为x元,则租赁公司的月收益为

∴当x=4 050时， f(x)取最值，最大值为

f(4 050)=307 050.

答：当每辆车的月租金定为4 050元时,租赁公司的月收益最大,最大月收益是307 050元.

19.(1)当a=-1时，

由图象可知函数的值域为[1,+∞).

(2)化简得

①a>1时，当x≥-1时，f(x)=(a+1)x+1是增函数，且f(x)≥f(-1)=-a;

当x<-1时，f(x)=(a-1)x-1是增函数，且f(x)

所以，当a>1时，函数f(x)在R上是增函数.

同理可知，当a<-1时，函数f(x)在R上是减函数.

②a=1或-1时，易知，不合题意.

综上可知，a的取值范围是

(-∞,-1)∪(1,+∞).

20.(1)由f(a+2)=18,得3a+2=18,即3a=2,∴a=log32.

(2)易知g(x)=λ·3ax-4x=λ·2x-4x.

设0≤x1

即(2x2-2x1)(λ-2x2-2x1)<0,即λ<2x2+2x1恒成立.由于2x2+2x1>20+20=2,所以实数λ的取值范围是λ≤2.