利用隐函数求导法解决一类二元最值问题

张 生 苏 猛

(内蒙古师范大学附属中学，010020)



利用隐函数求导法解决一类二元最值问题

张 生 苏 猛

(内蒙古师范大学附属中学，010020)

张朱艳老师在《中学数学》杂志(2015年第5期)中给出一类二元最值问题的解法及其本质探究,笔者读后受益匪浅.但同时也陷入对该类问题的又一思考中:一是解决此类问题的方法并不单一,但为什么学生还会感觉无从下手,难以掌握?二是此类问题一般都有明确的几何背景,那么,是否可以从其几何背景出发,找到解决问题的通性通法?带着上述疑问,笔者开始了新的探究与思考,得到解决此类问题的一种通用方法——隐函数求导法．

一、问题再现

原文中给出了以下两个问题,并给出了问题1的解法及几何背景分析．

问题1 (2011年浙江高考题)设x,y为实数,若4x2+y2+xy=1,则2x+y的最大值是______.

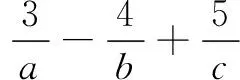
此类问题多出现在高考试卷中压轴小题的位置,也会出现在竞赛考试中,能够很好地考查学生的数学思维能力,起到选拔人才的作用．

二、对问题本质的再探究

原文对问题1的几何背景进行了全面分析,发现条件4x2+y2+xy=1对应的二元二次方程所表示的曲线为椭圆.所以，问题的本质即为椭圆4x2+y2+xy=1与动直线t=2x+y有公共点时,求t的最大值，即当直线与椭圆相切时,t取得最大值或最小值. 由此，原文从多解角度对问题进行解法展示,且都有一定的技巧性和运算量，对学生而言,不易系统掌握这些解法．

那么,如何有效运用问题的本质特征解题?关键在于解释直线与曲线相切这一几何特征．为此,我们给出求解此类问题的一种通用方法——隐函数求导法.既然是曲线与直线的相切问题,自然想到“设切点、求切点、代切点、得最值”这一解题步骤.由于在切点附近曲线可以看作函数图象,但不是显函数,所以可考虑采用隐函数求导法来确定切点的取值,进而求得最值；同时还可得到取最值时对应的x与y的值(即切点坐标)．

三、通性通法

基于以上分析,下面给出问题1、问题2的隐函数求导解题方法:

问题1的解法:问题1的本质为椭圆4x2+y2+xy=1与动直线t=2x+y有公共点时,求t的最大值,即当直线与椭圆相切时,t取得最大值或最小值．

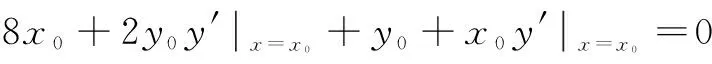
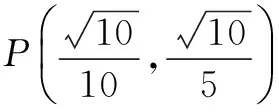
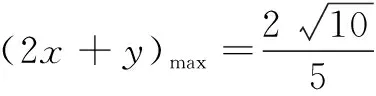
评注 隐函数求导法通常是方程两边对x求导，使用该方法的关键是求导时需视y为x的函数.

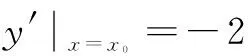
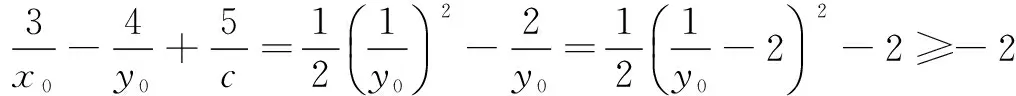
由以上解题过程可以得到以下解题的一般步骤:

第一步:分析问题模型,将问题转化为直线与曲线相切问题;

第二步:设出切点,利用隐函数求导法确定切点;

第三步:代入切点计算最值．

以上步骤是解决该类问题的通性通法,有效回避了解题所需的构造、换元、配凑、放缩等技巧,易于学生系统掌握．

基于上述解题步骤,下面给出问题3的隐函数求导解题法.

问题3 (2010年重庆高考题)已知x>0,y>0,x+2y+2xy=8,则x+2y的最小值是( )

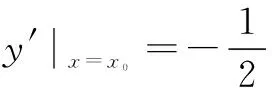
四、结论生成

由以上解题活动,可得出如下结论:

结论1 若关于x,y的二元二次方程ax2+bxy+cy2+dx+ey+f=0满足b2-4ac<0,则可求t=mx+ny的最值,当且仅当直线t=mx+ny与曲线ax2+bxy+cy2+dx+ey+f=0相切时取得最大(小)值．

结论2 已知关于x,y的二元二次方程axy+bx+cy+d=0 (x>0,y>0),则可求t=mx+ny的最大值或最小值,当且仅当直线t=mx+ny与曲线axy+bx+cy+d=0 (x>0,y>0)相切时取得最大值或最小值．