一道焦半径拓展题的探究
2016-12-17 02:43:51倪铭宏
高中数学教与学 2016年23期
倪铭宏
(江苏省靖江高级中学高三学生,214500)
○学生习作○
一道焦半径拓展题的探究
倪铭宏
(江苏省靖江高级中学高三学生,214500)
一、问题的提出
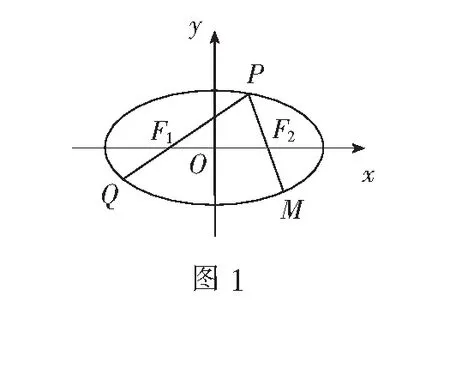
二、问题的思考
我从多方面进行了探究.探究中发现都与一个等式有关,我们就先来证明这一等式,为了便于说明,不妨称之为椭圆焦半径倾斜角等式.



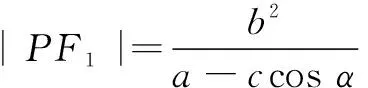
而当α大于90°时,在∆PF1L中,有

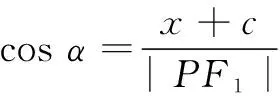


三、问题的解决
下面借助“椭圆焦半径倾斜角等式”,解决|PQ|+|PM|的取值范围问题.
解 设∠PF1F2=θ,∠PF2F1=γ,|PF1|=r1,|PF2|=r2.
由“椭圆焦半径倾斜角公式”,可得

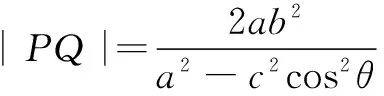
在∆PF1F2中,由余弦定理,得
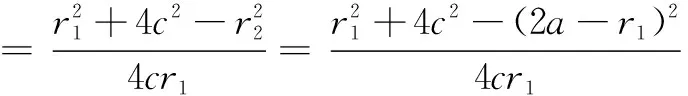


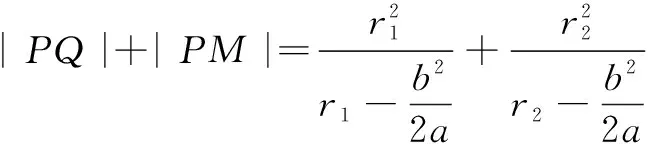

设t=r1r2,则t=r2(2a-r2),
结合a-c≤r2≤a+c,可得b2≤t≤a2.









四、问题的反思

思考1 “椭圆焦半径倾斜角等式”的证明可以用极坐标来完成,这里只简单说明.以椭圆的左焦点为极点,x轴正方向为极轴的方向建立极坐标系,则椭圆方程为
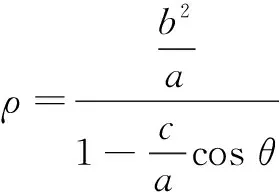
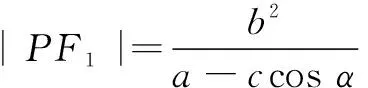
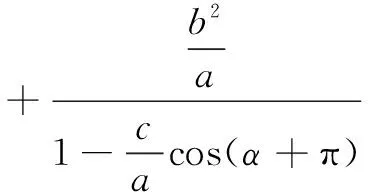
思考2 用余弦定理证明

事实上,用余弦定理化去cos β,cos α,得



思考3 用基本不等式证明



又∵|PQ|+|PM|=|QF1|+|MF2|+|PF1|+|PF2|=|QF1|+|MF2|+2a,
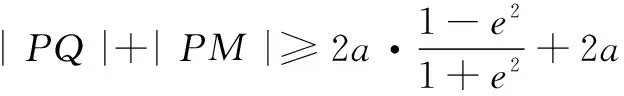

当且仅当r1=r2时,取等号.
我还进行了其它方面的探索,有些还不成熟,但是通过这样的探索,有很多感悟,最重要的感悟是:数学虽然较难,但是经过探索后,有一种成功的喜悦.
猜你喜欢
疯狂英语·初中天地(2023年3期)2023-10-25 16:53:09
江苏安全生产(2022年3期)2022-04-19 10:47:20
中老年保健(2021年11期)2021-08-22 03:17:06
华人时刊(2021年21期)2021-03-09 05:31:34
中学生数理化(高中版.高二数学)(2020年11期)2020-12-14 07:36:32
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27 03:04:28
河北理科教学研究(2020年2期)2020-09-11 06:15:56
河北理科教学研究(2020年1期)2020-07-24 08:14:28
电子测试(2018年14期)2018-09-26 06:04:14
智富时代(2017年4期)2017-04-27 02:13:48

