纯电动汽车白车身耐撞性拓扑优化设计方法

雷正保，刘助春，廖 卓

(长沙理工大学 汽车与机械工程学院，湖南 长沙 410004)



纯电动汽车白车身耐撞性拓扑优化设计方法

雷正保，刘助春，廖 卓

(长沙理工大学 汽车与机械工程学院，湖南 长沙 410004)

由于车辆碰撞工况多达9种且不同工况的碰撞力相差很大，对车身进行多工况并行拓扑优化时最终的整体拓扑构型会更加趋向于碰撞力大的工况，且车头、乘坐区、车尾由于碰撞力不同，最佳优化质量比也不同，故不能同时对整个车身进行多工况耐撞性拓扑优化.为得到一个材料分布合理有效的整车构型，通过对同一模型进行整体拓扑优化与分区域拓扑优化的对比分析，提出一种先进行乘坐区拓扑优化，然后在乘坐区结构已知的情况下，对车头、车尾拓扑优化，最后拼装成整车拓扑优化模型的白车身耐撞性拓扑优化设计方法.

纯电动汽车；耐撞性；拓扑优化；白车身

0 引言

传统的拓扑优化方法都是基于灵敏度分析，适用于解决线性静态问题.但在碰撞类的动态分析中，由于载荷与边界条件的瞬时性之间的复杂交互作用，灵敏度太难获得，因此，这种常规的基于灵敏度的拓扑优化分析并不适用于碰撞类问题[1-6].为了解决动态拓扑优化问题，国外学者Inou等[7]率先将自动网格模型(CA)与拓扑优化方法相结合；Patel等则在INOU等的基础上整合SIMP插值模型，提出一种以获得结构统一内能密度为目标的耐撞性拓扑优化方法—混合元胞自动机(HCA)[8]；Marklund利用二次响应面及线性响应面分别建立质量与速度的近似模型，针对侧撞工况对B柱进行耐撞性优化设计[9].目前国内对于耐撞性拓扑优化的研究很少.文献[10]运用耐撞性拓扑优方法对某车辆的门槛梁进行40 %偏置碰撞和侧面碰撞的并行拓扑优化；文献[11]对保险杠横梁进行基于混合元胞自动机的耐撞性拓扑优化.以上研究主要集中在车身单个零部件的优化上，尚无人对整个车身结构进行耐撞性拓扑优化的研究.

车辆碰撞工况较多，车头、乘坐区各涉及4种工况，车尾涉及1种工况，不同工况对应的关键安全性部件不同(如正碰的安全性主要由头部构型决定).把不同工况对应的关键安全性部件分开进行对应碰撞工况的拓扑优化，不仅能节省计算成本，且得出的拓扑构型由于只受其对应工况的影响更具有针对性，更能满足相应工况的安全性.此外，车辆不同碰撞工况的碰撞力相差极大，而工况的碰撞力越大，该工况对拓扑构型的影响也越大.若同时对整个车身进行多工况拓扑优化，则会出现碰撞力较大的工况对应的关键安全性部件材料堆积过多，无明显轮廓构型；碰撞力较小的工况对应的关键安全性部件的材料被删减过多，得出的构型不合理，而且车头、乘坐区、车尾由于碰撞力不同，需要的最佳优化质量比也不同，无法同时进行拓扑优化.故笔者先对乘坐区进行耐撞性拓扑优化，然后以乘坐区的拓扑优化结果为基础建立车头、车尾拓扑优化模型，进行车头、车尾的拓扑优化，最后拼装成整车拓扑构型.

1 耐撞性拓扑优化准则

混合元胞自动机(HCA)是利用元胞自动机CA单元来建立模型，通过有限元仿真方法获得模型信号的优化算法.该算法不需要计算灵敏度，能够有效解决瞬态非线性的连续拓扑优化问题.CA元胞单元的信息只被该单元和邻近单元的状态所决定，其利用相邻的单元信息来实现自身信息的更新重组，其结果是所有周围单元的平均值.

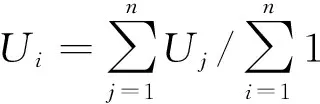
(1)

1.1 材料参数

使用密度法参数化，将设计变量直接链接到单个材料单元，使每个变量都有自己的材料模型.材料性质则是通过插值模型来获得，使用幂次法则驱动中间材料特性向边界移动去获得构型.根据SIMP模型[12-13]，材料属性可被定义如下：

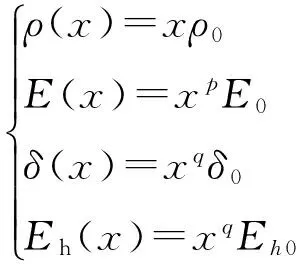
(2)

式中：ρ是材料密度；E是杨氏模量；δ是屈服应力；Eh是机械硬化模量；x是设计变量，在0～1变化，其中0表示空的，1表示满材料.

1.2 设计目标和约束

对于碰撞类的动态拓扑优化问题，往往要求结构在吸收最大能量的同时保持结构的稳定性，故以统一内能密度为动态拓扑优化的目标，则该优化问题可被表述为：

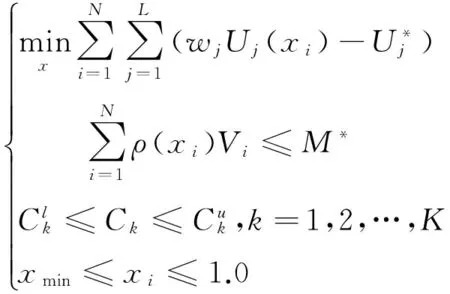
(3)

式中：U表述第i个单元的内能密度;Vi表述第i个单元的体积;U*代表目标内能密度;Ck代表k单元的约束;L为工况个数;K为约束个数;其中l与u分别表示约束的上、下限.

1.3 仿真获取场变量

第i个单元在第t个迭代的场变量的数值是前3个迭代的场变量的加权和,

(4)

1.4 更新规则

当总质量满足约束后，变量在此次迭代中的总变化就会被计算出来，并且将不再更新，如果不满足，则继续循环迭代直至满足质量约束.

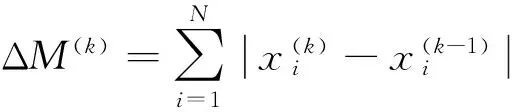
(5)

当质量的改变量小于设定的公差值，迭代停止.

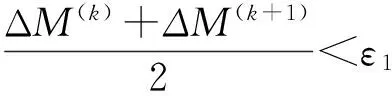
(6)

式中：ε1为质量收敛误差因子，取0.001.

2 整体与分区域拓扑优化对比

2.1 整体拓扑优化

整体拓扑优化模型如图1所示，固定横梁的两端，以整根横梁为初始优化区域，左、中、右3根立柱分别从不同位置以13 888 mm/s的速度垂直撞向横梁，两边的立柱的重量是中间立柱重量的三分之一，优化区域目标质量分数为0.25.经过43个迭代后，最终收敛的拓扑优化结果如图2.

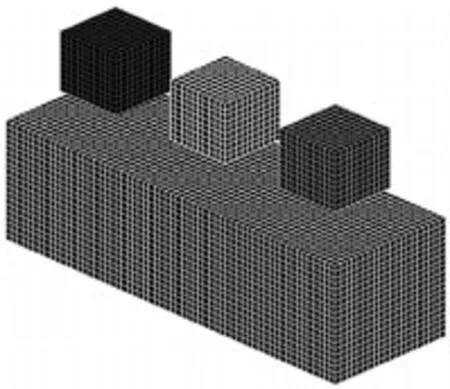
图1 整体拓扑优化模型

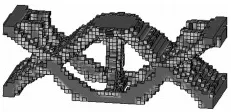
图2 横梁拓扑构型

由图2拓扑构型可看出，由于中间立柱的重量是两边立柱的3倍，其碰撞力也更大，故横梁中间部位保留的材料比两边多，表明拓扑构型更加趋向于碰撞力较大的工况.

2.2 分区域拓扑优化

分区域拓扑优化模型如图3所示，工况设置跟整体拓扑优化相同，将横梁分成左、中、右3个区域，先分别以两端为初始优化区域，得到两端的拓扑构型，如图4.然后以两端的拓扑构型为基础，建立中间拓扑优化模型如图5，以中间部分为初始优化区域.经过40次迭代，得出拓扑构型如图6.对比图6与图2可知，先优化两端后优化中间得出的构型与整体优化的构型有较大差别.故改变优化顺序，先以中间部分为初始优化区域，对此模型进行先优化中间后优化两端的分区域拓扑优化，先优化中间时中间收敛构型如图7.以中间收敛构型为基础重新建立两端拓扑优化模型如图8.

经过42次迭代，最终得到收敛构型如图9.对比图9与图2可看出，先优化中间后优化两端得出的拓扑构型跟整体拓扑优化得出的构型基本一样，说明进行分区域拓扑优化时，先进行中间拓扑优化后进行两端拓扑优化是可行的，而先优化两端后优化中间则误差较大.

图3 分区域拓扑优化模型

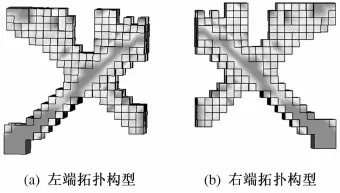
图4 左右端拓扑构型

图5 中间拓扑模型

图6 中间部分拓扑构型

图7 中间收敛构型

图8 两端拓扑优化模型

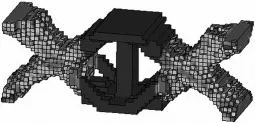
图9 收敛构型

3 白车身分区域耐撞性拓扑优化

车辆碰撞工况较多且不同工况对应的碰撞力相差很大，若同时对整车进行优化会导致最终的整体拓扑构型会更加趋向于碰撞力大的工况，且车头、乘坐区、车尾由于碰撞力不同，需要的最佳优化质量比也不同，故无法同时对整车进行多工况拓扑优化。由前文对同一模型进行整体拓扑优化与分区域拓扑优化的分析可知，先进行中间拓扑优化后进行两端拓扑优化的分区域拓扑优化是可行的，故先对乘坐区进行耐撞性拓扑优化，然后在乘坐区结构已知的情况下，进行车头、车尾拓扑优化，最后将三部分拼装得到整车拓扑优化结果.

3.1 乘坐区拓扑优化

依据某国产品牌纯电动汽车的技术参数建立纯电动汽车乘坐区拓扑优化模型，为了寻找最有效的载荷传递路径，最大化地拓展车厢设计空间，故模型扣除了行李舱、动力总成和风窗玻璃等部件，具体如图10所示.

将乘坐区作为初始优化设计区域，对其在弯曲载荷、顶压载荷及扭转载荷工况下进行拓扑优化.在拓扑优化中，质量分数对最终的拓扑优化结果的影响较大[15].选取质量分数α=0.1时构型的材料删减过多，没有连接成连续体结构.而α=0.3时，保留的材料过多，无明显的空间骨架结构特征，这两个质量分数约束下都不是理想的材料保留规则.重新进行拓扑优化设定后，最终选取α=0.2，经历新的迭代计算后得到了如图11的拓扑优化结果，此时结果保留了清晰的应力传递区域范围和乘坐区车身承力布局.

图10 乘坐区拓扑优化模型

图11 乘坐区拓扑优化结果

3.2 头部拓扑优化

结合收敛规则并与实际进行对比分析，对拓扑结果进行简化和抽象提取可得乘坐区构型，以得到的乘坐区构型为基础，依据GB11551—2003和欧洲正面碰撞法规ECE 894.01建立100%全宽碰撞有限元模型与40%偏置碰撞有限元模型.由于纯电动汽车是由电机驱动车辆，传统燃油汽车机械传动系统所占的空间全部释放[14]，故无发动机等一系列高强度高刚度的承力部件等，具体如图12所示.

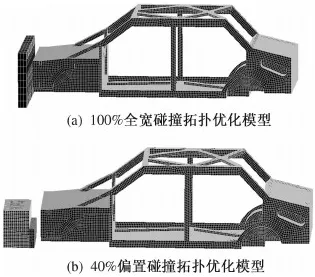
图12 头部拓扑优化模型

将车头作为初始优化设计区域，其余部件作为非优化区域，对头部结构施加关于纵向平面对称约束，进行100%全宽碰撞与40%偏置碰撞的并行耐撞性拓扑优化.根据汽车碰撞事故的概率分布，将全宽碰撞模型权重设为1.6，40%偏置碰撞模型权重设为1.2.选取质量分数为0.2，经过45个循环迭代运算后，构型收敛如图13.

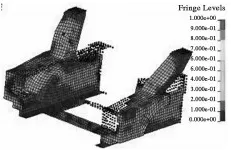
图13 头部拓扑优化结果

3.3 尾部拓扑优化

根据中国汽车追尾碰撞的技术规范GB20072—2006建立追尾碰撞试验有限元模型，台车及刚性移动壁的总质量为1 100 kg，具体如图14所示.

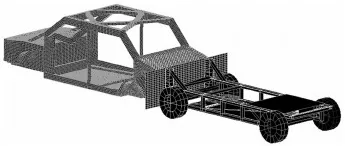
图14 尾部拓扑优化模型

将车尾作为初始优化设计区域，设定质量分数为0.25 此质量分数下尾部构型经过40次的迭代后收敛，最终的拓扑优化结果如图15.

图15 尾部拓扑优化结果

结合实际车形及收敛规则，对各区域拓扑优化结果进行抽象处理与简化，最终拼装成整车构型如图16.该整车构型应力传递区域范围和承力布局清晰明确，材料分布合理有效，进一步说明分区域分步式拓扑优化适用于白车身.

图16 整车拓扑构型

4 结论

通过对同一模型进行整体拓扑优化与分区域拓扑优化的对比分析，发现进行分区域拓扑优化时，先进行中间拓扑优化后进行两端拓扑优化是可行的，而先优化两端后优化中间则误差较大，故提出一种先进行乘坐区拓扑优化，再进行头部与尾部拓扑优化，最后拼装得到整车拓扑构型的纯电动汽车白车身耐撞性拓扑优化设计方法.该优化方法通过对车身不同区域分开进行对应工况的拓扑优化，使各区域能各自独立的按照其所需最佳质量分数进行材料删减，最终得到一个材料分布合理有效的整车构型，这对于提高整车耐撞性具有重要的意义.

[1] LEI Z B, HE R, LEI M X. Validating analysis on Influence of vehicle structure in considering crash compatibility[J]. Applied Mechanics and Materials Vols, 2012(29): 209-211.

[2] PATEL N M, KANG B S, RENAUD J E, et al. Crashworthiness design using topology optimization[J]. Journal of Mechanical Design, 2009, 13(6): 12-24.

[3] 舒磊,方宗德.汽车子结构的复合域拓扑优化[J]. 汽车工程, 2008,30(5): 35-37.

[4] 焦留成,邵创创,程志平.一种求解连续空间约束优化问题的蚁群算法[J]. 郑州大学学报(工学版), 2015,36 (1): 20-23.

[5] 李银霞,刘曼曼,高俊杰.汽车人机工程综合评价指标体系研究[J]. 郑州大学学报(工学版), 2014, 35(5): 96-99.

[6] BENDOSE M P, KIKUCHI N. Generating optimal topologies in structural design using homogenization method[J]. Computer Methods in Applied Mechanic and Engineering, 1998(2): 197-224.

[7] INOU N, SHIMOTAI N, UESUGI T. Cellular automaton generating topological structures[C]//Second european conference on smart structures and materials. glasgow, UK, 2011: 47-50.

[8] PATEL N M, KANG B, RENAUD J E, et al. Crashworthiness design using topology optimization[J]. Journal of Mechanical Design, 2009(6): 13-61.

[9] MARKLUND P O, NILSSON L. Optimization of a car body component subject to side impact[J]. Structural and Multidisciplinary Optimization, 2001(21):383-392.

[10]聂昕,黄鹏冲,陈涛,等.基于耐撞性拓扑优化的汽车关键安全件设计[J]. 中国机械工程, 2013, 23: 3260-3265.

[11]高云凯, 张玉婷, 方剑光. 基于混合元胞自动机的铝合金保险杠横梁设计[J]. 同济大学学报(自然科学版), 2015(3): 456-461.

[12]ROZVANY G I N, BENDOSE M P, KIRSH U. Optimality criteria a basis for multidisciplinary optimization[J]. Appl Mech Re, 1994(48): 114-119.

[13]YOON G H, KIM Y Y. Topology optimization of material-nonlinear continuum structures by the element connectivity parameterization[J]. Int J Numer Methods Eng. 1997, 69: 2196-2218.

[14]雷正保,李铁侠,赵仕琪.多目标拓扑优化下电动汽车头部结构优化设计[J]. 中国科技文,2014(11): 1324-1328.

[15]雷正保,何茹,王瑞.纯电动汽车正面碰撞相容性车头拓扑优化设计[J]. 计算力学学报, 2014(06): 722-728.

Crashworthiness Topology Optimization Method of Pure Electric Car BIW

LEI Zhengbao, LIU Zhuchun, LIAO Zhuo

(Institute of Vehicle Engineering, Changsha University of Science and Technology, Changsha 410004, China)

As the vehicle collision condition up to 9 kinds and the impact force of different conditions vary greatly,the final overall topology configuration will tend to working conditions with bigger collision force when multiple parallel topology optimization are used in whole body.What’s more, the best optimization mass ratio of front, car and rear is different for their different collision force. Thus multiple crashworthiness topology optimization can not be used in the whole body simultaneously. In order to obtain a vehicle configuration with reasonable and effective material distribution,we put forward a crashworthiness topology optimization method of pure electric ear BIW by the comparative analysis of the overall topology optimization and subregion topology optimization of one model.The method is doing the car topology optimization at first and doing the head and rear topology optimization after we get car topologies,in this way we obtain the vehicle topology optimization results finally.

pure electric vehicles; crashworthiness; topology optimization; BIW

2016-03-28；

2016-05-18

国家自然科学基金资助项目(51175050)

雷正保(1964—)，男，长沙理工大学教授，博士，主要从事汽车安全技术研究，E-mail:doclei@foxmail.com.

1671-6833(2016)05-0077-05

U270.2

A

10.13705/j.issn.1671-6833.2016.05.015