OFDMA系统多业务频谱切换策略的CPN建模及性能评价

陆彦辉，李兆平，2，韩书君，杨守义

(1.郑州大学 信息工程学院, 河南 郑州 450001； 2.河北省长途通信传输局 石家庄传输局，河北 石家庄 050051)



OFDMA系统多业务频谱切换策略的CPN建模及性能评价

陆彦辉1，李兆平1，2，韩书君1，杨守义1

(1.郑州大学 信息工程学院, 河南 郑州 450001； 2.河北省长途通信传输局 石家庄传输局，河北 石家庄 050051)

为保障用户的不同服务要求，对不同业务执行区分服务并实现频谱切换管理是通信系统亟需解决的主要问题之一.研究切换问题的传统方法是Markov建模，Markov模型具有无记忆特性，并且易于产生状态空间爆炸问题，这使得频谱切换策略的研究大多停留在单业务OFDMA系统.应用着色Petri网(colored petri nets, CPN)开发适用于多业务OFDMA系统的频谱切换策略，建立了4种兼顾切换用户和新到用户传输性能的频谱切换策略的CPN模型.仿真结果表明，CPN能够克服Markov模型的局限性，便于分析复杂系统，特别是到达规律服从多种数学分布的多业务系统频谱切换策略.

频谱切换；Markov；着色Petri网；多业务；数学分布

0 引言

频谱切换是无线资源管理的一项重要技术[1]，能够满足用户通信服务质量要求的条件下，最大限度的提高资源利用率和系统容量，同时避免系统拥塞.一项好的频谱切换策略，不仅能够保障用户的通信质量[2]，而且能够满足多用户共存的不同通信需求，使系统资源分配更科学合理[3].

OFDMA系统将传输带宽划分成一系列正交的互不重叠的子载波，把不同的子载波集分配给不同的用户实现多址，从而实现系统资源的优化利用[4]，成为4G和未来移动通信系统的关键技术之一.目前，关于频谱切换策略的研究大多是基于认知无线电系统或CDMA系统[5]，针对多业务系统尤其是OFDMA多业务系统频谱切换策略的研究成果较少，且现有的多业务系统研究是应用Markov理论分析[6-7].多业务系统的Markov模型结构十分复杂，易产生状态空间爆炸[8].因此，1997年，Fernando J.等[9]使用Petri网建立了无线资源管理模型.马玉琨等[10]于2009年采用随机Petri网(stochastic petri nets, SPN)实现了OFDMA系统的接纳控制模型.虽然已经证实SPN能够克服Markov模型的无记忆特性[11-12]，但SPN与Petri网的共同之处是没有数据概念和层次概念，因而所有模型结构和数据操作都是建立在同一层次内.当系统较为复杂时，尤其业务到达规律为非指数分布时，SPN同样会出现状态空间爆炸问题.CPN与SPN类似，属于高级Petri网，能够模拟多种复杂系统[13]，具有很强的可视性结构[14-15]，其分层结构能克服状态空间爆炸问题.

笔者使用CPN模型与Markov模型研究单业务系统的频谱切换策略分析方法，并搭建多业务系统中频谱切换的CPN模型，提出4种不同的频谱切换策略.最后设计了业务到达服从多种数学分布的CPN模型，并使用CPN Tools进行仿真.

1 多业务系统中频谱切换的CPN模型

假设OFDMA多业务通信系统中同时存在实时用户和非实时用户两类，各类用户又分别包含新到用户和切换用户.因此，系统中同时存在实时新到用户、实时切换用户、非实时新到用户和非实时切换用户.4种用户相互统计独立，用户到达服从泊松分布，用户离开服从负指数分布，相应参数如表1所示.

图1为多业务系统一般化模型的CPN结构，由7个变迁和5个库组成.7个双线框代替各自的子页面，表示7个事件的发生.“信道估计”是对系统空闲资源的统计，“资源分配”实现频谱切换策略，另外4个变迁分别代表相应用户到达.不同切换策略的区别主要存在于资源分配页面.

表1 多业务系统中用户参数

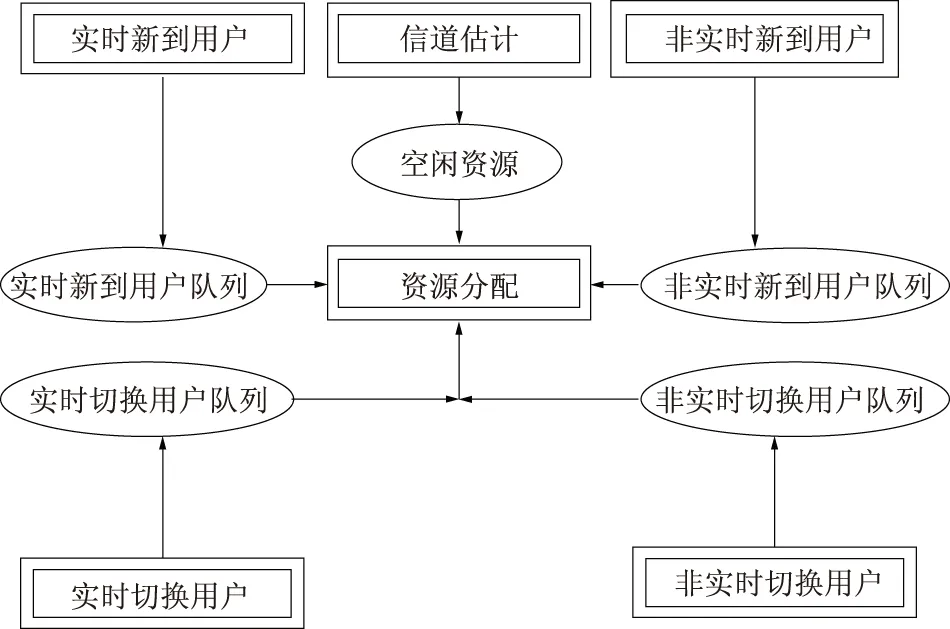
图1 多业务系统一般化模型的CPN结构图

2 模型分析

2.1 传统Markov模型的单业务分析方法

假设系统中的一类业务包括新到用户和切换用户，其中，新到用户与切换用户工作时需占用的信道数相同，新到用户到达率为λn，切换用户到达率为λh.系统中的新到用户和切换用户的数目比例设为2∶1，因此λh=λn/2.用户的到达和离开统计独立，已有的相关研究中大都将新到用户和切换用户视作两种业务，设置两种用户离开率，本文中，同一类业务的新到用户和切换用户设置相同服务率μ.系统为切换用户预留N0个资源，即当系统可用资源大于N0=N-m时，可同时为新到用户和切换用户分配资源，否则，不为新到用户分配资源.为了与传统分析方法对比，笔者给出Markov排队模型的状态图，如图2所示.k表示系统中被占用资源数，P(k)表示k状态存在的概率.被占用资源数小于m时，资源可分配给新到用户和切换用户；被占用资源大于m时，资源只分配给切换用户.

由状态图分析可得

图2 单业务资源预留的排队模型

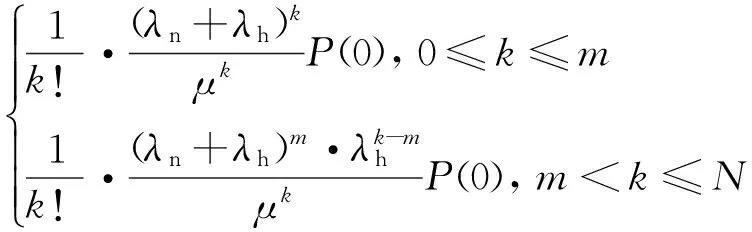
(1)

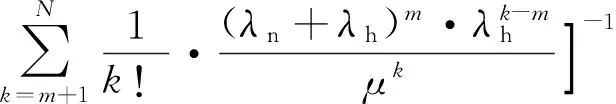
(2)

因此，新到用户阻塞率为

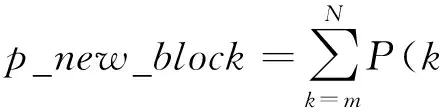
(3)

切换用户阻塞率为

p_handoff_block=P(N).

(4)

2.2 4种不同的多业务频谱切换策略

资源分配的设计原则：①切换用户优先于新到用户；②缓冲队列中的等待用户优先于一般新到用户；③实时用户优先于非实时用户.

切换用户进入系统时可用资源充足，则为切换用户分配资源；可用资源不足，则阻塞切换用户.新到用户的资源分配方案如图3所示.

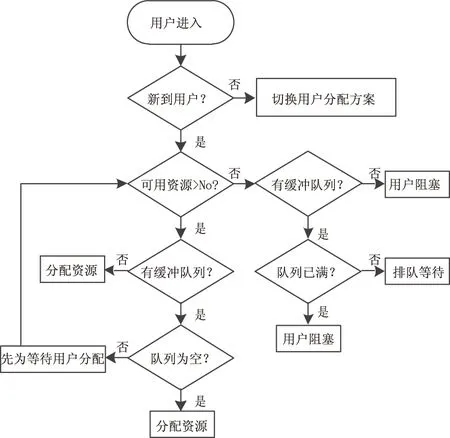
图3 新到用户资源分配方案

表2为4种多业务频谱切换策略的设计方案及各用户的优先级.由单业务分析方法可知，资源预留数越多，优先级对新到用户的抑制作用越大.

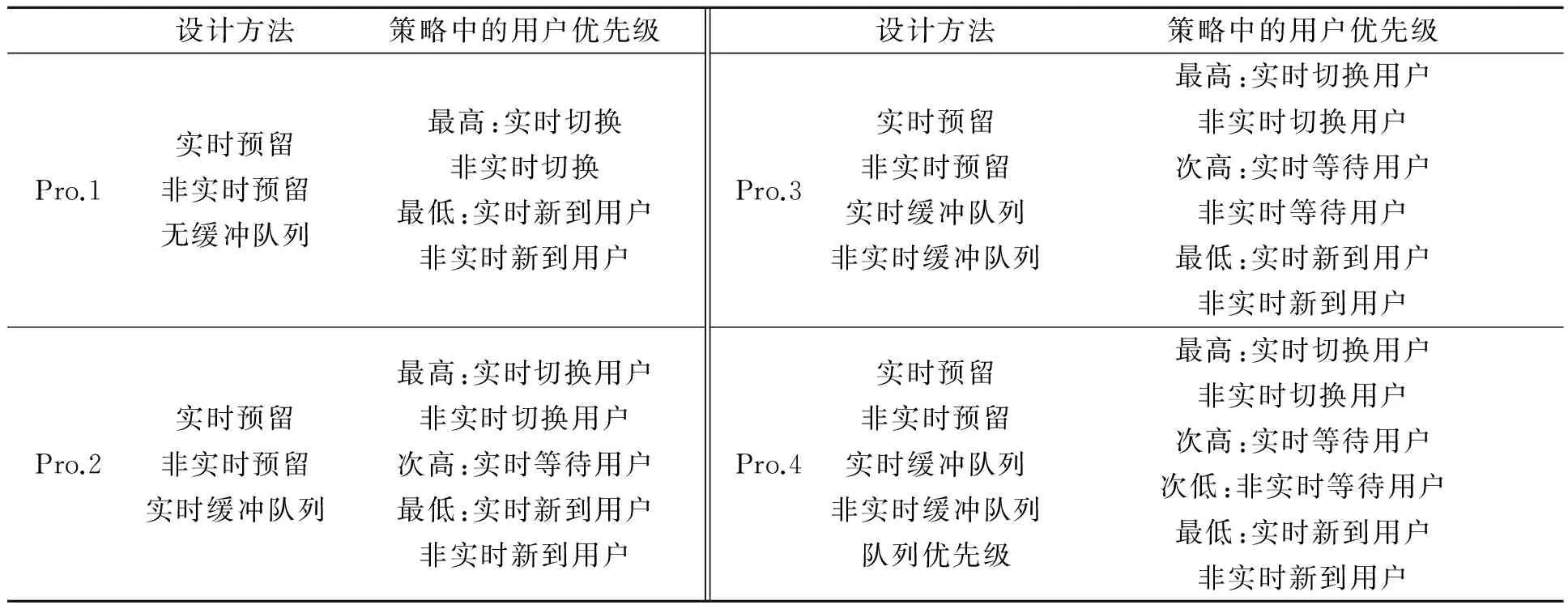
表2 4种多业务频谱切换策略

为了方便分析，将实时与非实时切换用户的资源预留数目设为相同.考虑新到用户的利益，Pro.2、Pro.3和Pro.4通过添加缓冲队列，增加新到用户分得资源的机会.Pro.4中设置缓冲队列的优先级，使实时等待用户的优先于非实时等待用户.

2.3 业务到达服从多种分布的CPN模型

传统Markov模型分析方法中，业务到达服从泊松分布，改变到达规律意味着整个模型的重新计算.而CPN模型中只需要改善业务到达的控制模块，即可从仿真结果中得出相应分析结果.

图4为用户到达规律的设置，用户按照泊松分布进入系统，由变迁“用户到达”实现.更改变迁控制函数，即可实现用户到达服从泊松分布、正态分布、均匀分布等数学分布.

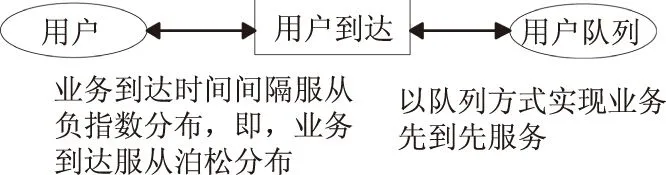
图4 用户到达页面

多分布CPN模型的设计选取多业务系统Pro.4策略，将实时用户的到达和离开均设置为正态分布，非实时用户设置为均匀分布.

3 仿真结果分析

仿真中系统信道总数N=50，实时用户工作占用资源数a=1，非实时用户占用资源数b=2.切换用户到达率λh1=λn1/2，λh2=λn2/2.系统对用户的平均服务时间为1/μ1=1/μ2=100 s.新到用户和切换用户到达强度为λn/μ和λh/μ.资源预留数目N0=3,等待队列长度k=3.

图5为CPN模型与传统Markov排队模型的数据结果，其中N0=0表示未设置任何优先级，此时新到用户与切换用户的阻塞率曲线变化相同.

图5 单业务分析方法的仿真曲线

从图5中可以看出，相同条件下CPN与Markov排队模型的数据结果完全吻合.资源预留策略使得切换用户阻塞率明显降低，其代价是新到用户阻塞率升高.系统为切换用户预留的资源数越多，新到用户阻塞率就越高.考虑新到用户阻塞率不宜过高，一方面适当控制预留资源数，另一方面为新到用户添加缓冲队列.

图6、图7为4种方案中实时用户、非实时用户阻塞率变化曲线.Pro.2比Pro.1添加了实时等待队列，增加了实时用户分得资源的机会，相应减少了其他用户分得资源的机会，因此图6(a)中Pro.2比Pro.1低，图7(a)中Pro.2比Pro.1高.同理，Pro.3中比Pro.2添加了非实时新到用户等待队列，图6(a)中Pro.3比 Pro.2高，图7(a) 中Pro.3比 Pro.2低.Pro.4与Pro.3对比，实时等待用户优先于非实时等待用户，因此图6(a)中Pro.4比Pro.3低，图7(a)中Pro.4比Pro.3高.

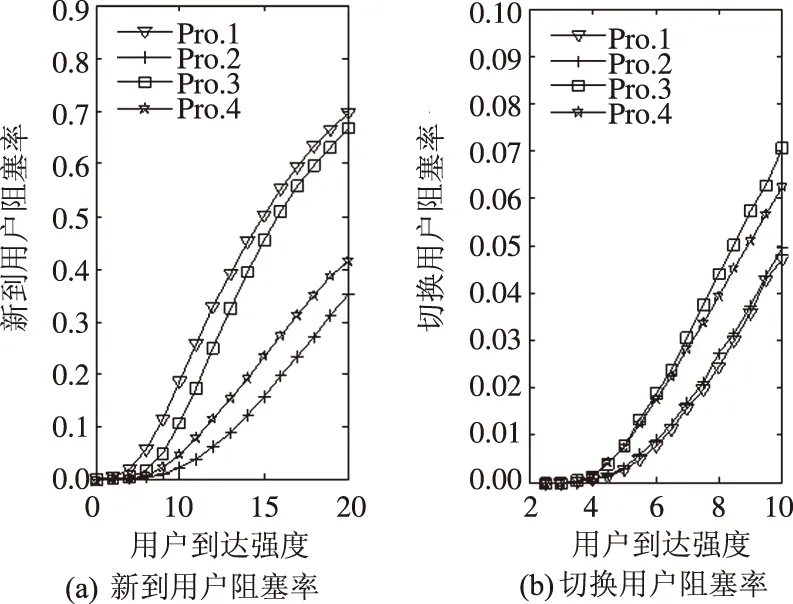
图6 多业务实时用户各方案对比

图7(a)中可以看出非实时新到用户的阻塞率对比中Pro.1和Pro.4存在交点.原因是Pro.4比Pro.1增加了2个等待队列和1个优先级设置.交点之前，用户到达强度较低，等待队列的缓冲作用大于优先级的抑制作用.随着用户到达强度的逐渐增加，优先级对非实时用户的抑制作用愈发明显，并逐渐超过等待队列的缓冲作用，因此，交点之后Pro.4的阻塞率会比Pro.1高.

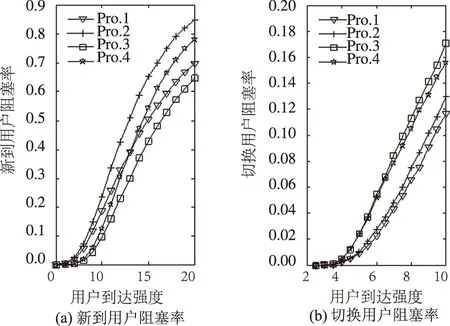
图7 多业务非实时用户各方案对比

图6(b)和图7(b)中，Pro.1～4中都为切换用户设置了资源预留，因此阻塞率十分接近.而Pro. 3和4比Pro.1和2多了新到用户等待队列，因此Pro.3和4比Pro.1和2阻塞率高.

图8为系统中用户到达服从不同数学分布时，各用户阻塞率随用户到达率的变化曲线.图中显示，两种分布下的实时用户阻塞率变化趋势相似，原因是正态分布可视作泊松分布的极限分布.而均匀分布与泊松分布之间不存在直接关系，因此这两种分布下的非实时用户阻塞率变化趋势差异较大.研究表明，CPN模型不但可以实现Markov语义的频谱切换模型，而且能够在已有模型中实现用户服从不同到达规律，从而克服了Markov无记忆特性问题.

图8 用户不同到达规律的阻塞率曲线

4 结论

CPN模型与Markov排队模型都可以通过采取资源预留策略和添加缓冲队列的方式改善部分用户的传输性能，实现单业务OFDMA通信系统的频谱切换策略.资源预留策略可以降低切换用户的阻塞率，但以提高新到用户阻塞率为代价.为新到用户添加缓冲队列，可以降低新到用户的阻塞概率，提高系统性能.与Markov模型相比，CPN模型可视性强，可以对现实复杂系统进行高度仿真与精确的性能分析，避免状态空间爆炸问题的出现.CPN模型中的多种数学分布功能满足了系统业务不同到达规律的需求，克服了传统Markov模型的无记忆特性问题.下一步的研究将细化不同用户的传输需求，使设计模型更接近实际应用.

[1] 陆彦辉. B3G移动通信系统中无限资源管理技术的研究[D]. 北京: 北京邮电大学信息与通信工程学院, 2006.

[2] WU C Y, HE C, JIANG L G. Spectrum handoff scheme based on recommended channel sensing sequence[J]. Communications China. 2013,10(8): 18-26.

[3] 张天魁，冯春燕. B3G/4G移动通信系统中的无线资源管理[M]. 北京：电子工业出版社，2011.

[4] 杨守义, 郝万明. 认知无线电中考虑公平性的OFDMA资源分配策略[J]. 郑州大学学报(工学版), 2014,35(3):55-59.

[5] TRIGUI E, ESSEGHIR M, BOULAHIA LM. Spectrum handoff algorithm for mobile cognitive radio users based on agents’ negotiation[C]. IEEE International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob). France:IEEE,2013, 750-756.

[6] SONG Y, XIE J. Prospect: a proactive spectrum handoff framework for cognitive radio ad hoc networks without common control channel[J]. IEEE Trans on Mobile Computing, 2012, 11(7): 1127-1139.

[7] TUMULURU V K, WANG P, NIYATO D, et al. Performance analysis of cognitive radio spectrum access with prioritized traffic[J]. IEEE Transactions on Vehicular Technology, 2012, 61(4): 1895-1906.

[8] LU Y H, ZHANG Y Q, YANG S Y， et al. Modeling radio resource management in cognitive radio system based on OFDMA using colored petri net[J]. Journal of Electronics, 2010, 27(5): 671-676.

[9] JAIMES R F J, MUNOZ R D, MOLINA C,et al. Modeling resource management in cellular systems using petri nets[J]. IEEE Transactions on Vehicular Technology, 1997, 46(2): 298-312.

[10]马玉琨, 陆彦辉, 杨守义. OFDMA系统中接纳控制的Petri网模型[J]. 系统仿真学报, 2009, 21(23): 7675-7677.

[11]ZENG R F, JIANG Y X, LIN C, et al. Dependability analysis of control center networks in smart grid using stochastic petri nets[J]. IEEE Trans on Parallel and Distributed Systems, 2012, 23(9): 1721-1730.

[12]JENSEN K, KRISTENSEN LM, WELLS L. Colored petri nets and cpn tools for modeling and validation of concurrent systems[J]. International Journal on Software Tools for Technology Transfer, 2007, 10(9): 213-254.

[13]黄阳. 基于着色Petri网的知识流建模及应用研究[D]. 南京：南京邮电大学管理学院, 2014.

[14]SCHOENEN R, YANIKOMEROGLU H. Erlang analysis of cellular networks using stochastic petri nets and user-in-the-loop extension for demand control[C]. Proceedings of the Globecom 2013 Workshop-broadband Wireless Access, USA:IEEE, 2013: 298-303.

[15]YAO Y Y, LU Y H, YANG S Y. Modeling multi-traffic admission control in OFDMA system using colored petri net[J]. Journal of Electronics, 2012, 29(6): 509-514.

The CPN Modeling and Performance Evaluation about Spectrum Handoff Strategies in OFDMA Multi-service Communication System

LU Yanhui1, LI Zhaoping1,2, HAN Shujun1, YANG Shouyi1

(1.School of Information Engineering, Zhengzhou University, Zhengzhou 450001, China; 2.Long-Distance Communication Transmission Shijiazhuang Sub-bureau of Hebei, Shijiazhuang 050051, China)

With the increasing diversified demand on communication system, the differentiation in multi-service is one of the major problems faced with the communication system on the premise of ensuring quality of service requirements of users. Markov model is the traditional way to study the switch problem, however, the memory-less quality and the state space explosion problem of the Markov model make the research about the spectrum handover strategies stay at the single business OFDMA system. This paper utilizes the Colored Petri Nets (CPN) to develop the spectrum switching strategies suitable for multiple business OFDMA system. Four different spectrum strategies considering both the switching users and new users are discussed using CPN model in this paper. The results show that CPN can overcome the limitation of Markov, and facilitate the research of the spectrum handoff quality about the complex system, especially the multiple business system contenting several mathematical distributions for the users’ arrival laws.

spectrum handoff; Markov; colored petri net; multi-service system; mathematical distribution

2016-03-30；

2016-06-27

新世纪优秀人才支持计划资助项目(NCET-12-0699)

陆彦辉(1972-),女,河南郑州人，郑州大学教授，博士，主要从事宽带无线通信、着色Petri网理论及应用研究，E-mail:ieyhlu@zzu.edu.cn.

1671-6833(2016)05-0057-05

TN929

A

10.13705/j.issn.1671-6833.2016.05.011