基于Spark的并行极速神经网络

邓万宇，李 力，牛慧娟

(西安邮电大学 计算机学院，陕西 西安 710121)



基于Spark的并行极速神经网络

邓万宇，李 力，牛慧娟

(西安邮电大学 计算机学院，陕西 西安 710121)

随着数据规模的快速膨胀，基于单机的串行神经网络结构面临着巨大的计算挑战，难以满足现实应用中的扩展需求.在极速学习机(extreme learning machine，ELM)基础上，基于Spark并行框架提出一种并行的极速神经网络学习方法，以Spark平台特有的RDD高效数据集管理机制对其进行封装，并将大规模数据中的高复杂度矩阵计算进行并行化，实现ELM加速求解，仅需一组Map和Reduce操作即可完成算法的训练.在大量真实数据集上的实验结果表明，基于Spark的并行ELM算法相较于串行ELM获得了显著的性能提升.

极速学习机；神经网络；并行化ELM算法；Spark

0 引言

极速神经网络(extreme learning machine，ELM)已被广泛应用于数据挖掘、模式识别等众多领域[1].相较于应用更为广泛的单隐藏层前馈BP神经网络，ELM具有隐藏层输入权及阈值可随机生成，有效克服了BP迭代次数过于频繁，计算量、内存开销及耦合性过大等问题，仅需要一次学习即可完成训练的优势.更重要的是，传统基于梯度下降的BP神经网络算法，以反向传播误差的方式对参变量进行迭代调整和网络训练，导致计算过程难以并行化，无法集成和发挥分布式计算平台的并行计算优势.因此，人们正努力构建各种更为高效的并行化计算框架或平台，通过汇集计算机节点与计算资源，将大规模数据进行并行化处理.MapReduce是大家熟知的一种高容错分布式计算框架，然而MapReduce计算过程中因重复加载数据导致的大量磁盘I/O操作非常耗时低效,使其难以成为构建高性能并行机器学习算法的开发平台[2-3].最近，Spark在解决磁盘I/O问题上被视为MapReduce的升级与替代者，Spark是一种基于内存的集群式计算平台，允许机器将数据缓存在内存中，从而避免了反复的磁盘I/O操作[4].此外，Spark采用一种全新的弹性分布式数据集(RDD)来解决容错问题，大大降低了容错不足导致的风险.单机串行ELM已经得到了深入研究，然而单机平台的容量与承载能力在面对大规模数据膨胀问题时正面临极大的挑战，为此笔者基于Spark提出一种并行神经网络极速学习方法，以Spark平台特有的RDD高效数据集管理机制对极速学习机进行封装，将大规模数据中的高复杂度矩阵计算进行并行化，实现ELM的并行加速求解.

1 Spark系统

传统的MapReduce框架在进行信息处理过程中需要对数据进行大量的磁盘I/O操作，并行效率较为低下.基于内存的分布式计算框架Spark很好的解决了频繁的磁盘I/O问题.Spark是一种高效的基于内存的多功能集群式计算平台，允许计算节点将中间结果缓存于内存中，从而解决了反复迭代等高密度计算过程中的磁盘频繁I/O操作.Spark主要包括分布式文件系统、弹性分布式数据集、容错机制等几个模块.

1.1 分布式文件系统

Spark沿用Hadoop平台所提供的分布式文件系统(hadoop distributed file system，HDFS)，这款文件系统设计之初就是为了便捷的存储及操作大规模数据，此外，HDFS内嵌了高容错性策略：①数据复写机制使同一份数据在多个节点产生副本.当一个节点发生故障，仍可对其他的节点的数据副本进行存取.②HDFS以心跳机制检测节点可用性.HDFS有唯一的主节点(namenode)及多个从节点(datanode)，主节点对HDFS文件系统命名空间进行管理，而从节点则用于以块为单位存储数据.从节点周期性发送心包跳给主节点，当主节点无法获取集群上某从节点的心跳包时，则认定该节点已经死亡，并且不再对该节点进行I/O操作.

1.2 弹性分布式数据集(RDD)

RDD主要由位于HDFS之上的分布式文件构造，或是由其他RDD转化而来.在Spark中数据被封装成一个包含多个分片的RDD，分片是指Spark中数据的分布式片段，是Spark缓存管理器加载的基本单元.每个从节点仅需要保存训练集的一部分分片,如果从节点内存充足，分片将被缓存于从节点内存中，否则存储于磁盘内.在同一时间区间内每个从节点仅需要管理本节点所持有的数据分片，而无需对整个数据集负责.该机制可令计算过程实现并行化.设有s个从节点以及p个分片，当指定p>s时，p个分片可以在s个从节点并行计算，从而充分实现并行化.Spark允许用户根据应用的具体需求指定不同的分片个数p.事实上，Spark根据用户的训练集大小给出一个最小分片个数pmin，当用户未指定p的值，或者所指定的p值小于pmin时，Spark将认为p=pmin.除此之外，Spark支持对RDD的两种并行操作，称为transformation和action，其中transformation用于从已存在的数据创建新的RDD，包括如map和filter等操作.而action则是对RDD进行计算，包括reduce和collect等.

1.3 Spark的容错机制

Spark拥有高容错性的关键在于只读权限的RDD，当数据集中某个分片丢失，Spark将申请对原始RDD进行transformation操作重新计算并创建分片信息.lineage机制用于保存并记录RDD之间的transformation操作，并以作为集中式元数据保存于主节点中.lineage可以保证对RDD进行有效的重新计算，并且只读权限的RDD可以保证如果需要重新执行lineage中已执行过的某个操作时，可以获得相同的计算结果.

2 ELM并行化实现

2.1 ELM算法描述

ELM由Huang于2004年提出[1]，单隐藏层前馈神经网络发展而来，但ELM相较于传统的单隐藏层前馈神经网络，仅需要对隐藏层节点的个数进行设置，并随机生成隐藏层偏差和输入权值，采以最小二乘法求得输出权值，仅一次计算而无需迭代，相较于BP等其他神经网络有显著的提高[5]，并具有优秀的泛化性能.

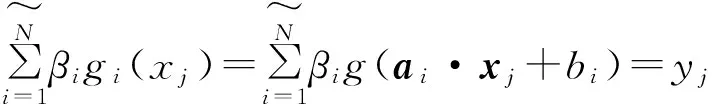
(1)

j=1,2,…,N.

其中:

xi=[xi1，xi2,…,xin]T∈Rn；

t1=[tt1,ti2,…,tin]T∈Rm.

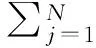
Hβ=T.

(2)

其中

式中：H为N个样本相关的隐藏层输出矩阵；β为模型输出权重，其最小二乘解为

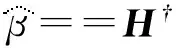
(3)

式中：H†为H的摩尔彭若思广义逆(Moore-Penrose generalized inverse).回归预测Y可表示为：

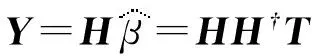
(4)

该多元回归的误差为：

‖e‖=‖Y-T‖=‖HH†T-T‖.

(5)

H†的求法主要包括正交投影法[6]，迭代法以及SVD分解法(single value decomposition)法[17]等.ELM算法描述如下：

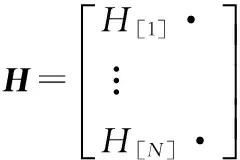
算法1 ELM算法给定N个独立训练样本集激励函数g(x)及隐藏层节点个数N.步骤1:随机分配输入权值和偏差:(ai,bi),ai∈RN,bi∈R,i=1,2,…,N～;步骤2:计算隐藏层输出矩阵H(a1,…,aN～,b1,…,bN～,x1,…,xN)=g(a1·x1+b1),…,g(aN～·x1+bN～)︙… ︙g(a1·xN+b1),…,g(aN～·xN+bN～)éëêêêêùûúúúúN×N～;={(xi,ti)|xi∈Rn,ti∈Rm,i=1,2,…,N}步骤3:计算输出权值:β^=H†T.

2.2 ELM算法并行化策略

ELM具有无需迭代、一次求解的优点.但隐藏层输出矩阵H，在训练样本较大时，存在存储、计算开销过大的缺点[8]；并且ELM需要将数据及中间结果载入内存，这在单节点情况难以实现.因此，如何减少磁盘I/O时间、内存开销，结合Spark平台基于内存操作的优势，是ELM并行化实现的关键.

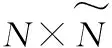
H†=inv(HT×H)×HT.

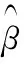
2.2.1 并行算法设计

其中:

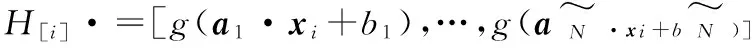
令Y=HT×H，Z=HT×T，则Y、Z可以表示如下

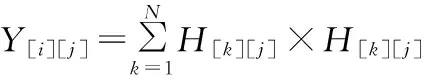
(6)

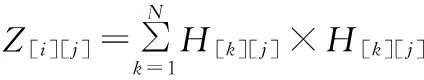
(7)

观察可知，不妨令Y的第i行向量

(8)

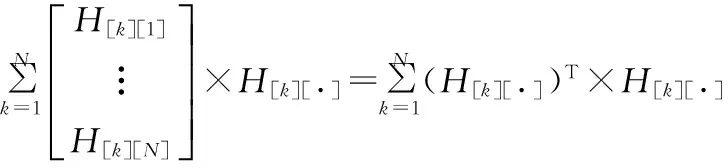
(9)

同理Z可表示为

(10)

经上述一系列推导，Y、Z的计算可以转化为对N训练样本独立并行化运算，并最终求和的

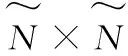
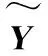
(11)

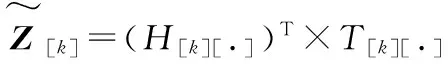
(12)

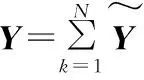
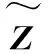
算法2、算法3将详细描述计算过程.

算法2 β^=H+T的分布式求解 步骤1:主节点构造输入权值和偏差向量(ai,bi),ai∈RN;bi∈R;i=1,2,…,N～,激励函数g(x),并将(a,b),g(x),N～以广播形式交给各从节点.步骤2:从节点调用算法3计算Y～[k]和Z～[k],并汇总各从节点结果,将Y=∑Nk=1Y～[k];Z=∑Nk=1Z～[k]交还主节点.步骤3:主节点以EVD分解,得到β^=inv(Y)×Z. 算法3:Y～[k]和Z～[k]的分布式求解 1:从节点得到输入权值和偏差向量(a,b),g(x),N～,当前训练样本的输入样本数组inarr,输出样本为out.2:定义空数组h作为样本的隐藏层输出向量;3:fori=1toN～;4:x=0;5:forj=1toInArr.length;6: x+=inputarr[j]×a[i][j] (a[i][j]为第j个输入神经元到第个i隐藏层节点的权值);7:endfor.8:h.append(g(x+b[i]))(将g(x+b[i])添加到h中,b[i]为第i个隐藏层节点阈值),9:endfor.10:定义长度为N～×N～的向量y,和长度为N的向量z,11:fori=1toN～,12:x=0,13:forj=1toN～,14: y.append(h[i]×h[j]) (将h[i]×h[j]添加到y中),15:endfor.16:z.append(h[i]×out)(b[i]为第i个隐藏层节点阈值),17:endfor.18:当前从节点得到单个样本的输出Y～[k]和Z～[k].

3 基于Spark的具体实现

3.1 数据的存储

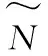
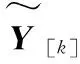
图1 类表示

Fig.1Classapproach

图2 数组表示

Fig.2 Array approach

类表示是将index-value对封装在类中，并以数组形式存储每一样本的一簇类对象：数组表示直接将index和value分别用两个数组进行存储.

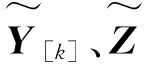
3.2 任务均衡MapPartition和Coalesce函数

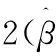
为减少主节点计算量，均衡计算任务，从节点在提交结果之前进行两级运算：第一级，选择Spark中的mapPartitions代替map函数，对每个分片内所有向量进行求和，一个分片仅产生唯一一组中间变量；第二级，调用Coalesce函数对当前节点内所有分片结果进行求和，最终每个节点仅产生一组结果，如图3.

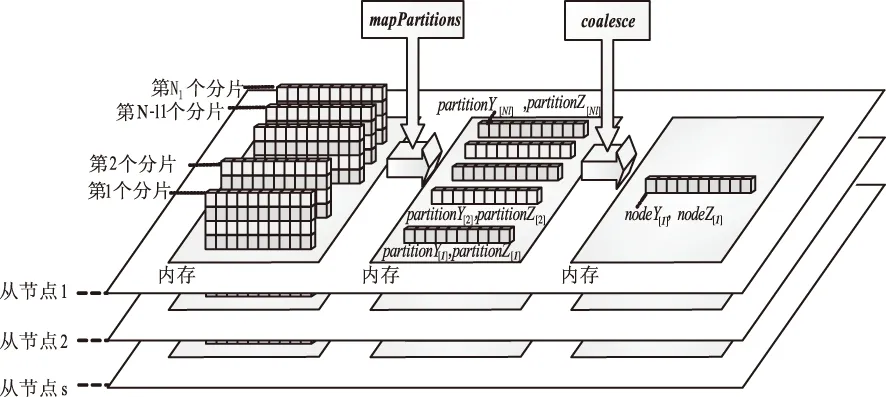
图3 任务均衡

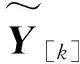
第二步，每个节点仅包含Ni组向量，为达到充分利用从节点计算资源的目的，在mapPartitions之后调用coalesce函数，同一从节点i的所有分片最终仅产生一组输出向量NodeY[i]，NodeZ[i](i∈s)：

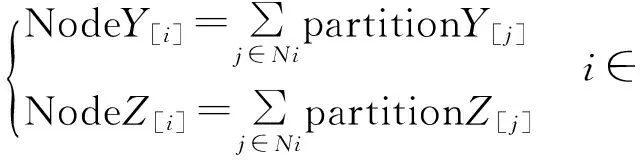
通过mapPartitions与coalesce相互使用，使得所有本地分片在从节点得以充分计算，令从节点提交到主节点的向量数量由N个下降至s，从而使计算任务得以均衡分配，算法并行度显著提高.

此外，稀疏向量的求和操作通过构造稠密向量进行，由于稠密向量包含所有列元素，因此可以与稀疏矩阵直接进行对位求和，从而避免反复构造索引数组与值数组.

3.3 broadcast(广播变量)

广播变量机制，是指将主节点的参数以只读形式缓存于从节点中，每个从节点仅保存一份副本，该节点内所有分片都可共享使用.

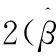
位于同一节点的所有分片可共享广播变量.

4 性能评估

为验证算法的性能，我们以不同规模的数据集对算法进行测试，并将SparkELM与SVM、BP、ELM等算法进行对比，主要以时间加速比(speed-up ratio)和测试精度(testing accuracy)进行评估.所使用数据集在LIBSVM数据集网站均可以下载[14].Spark实验平台为Debian操作系统机器，共7台机器，都为16 GB内存，四核Xeon E5440(2.83 G)，集群版本Hadoop 2.5.0、Java 1.7.0_74、Spark1.3.1.

4.1 数据集

选定卫星图像(satimage)、航空记录(shuttle)等4种真实的分类数据集以及汽车价格(autoPrice)、股票价格(stocks)等9种回归数据集对SparkELM算法的性能进行验证.回归数据集信息如表1，分类数据信息如表2所示.

表1 回归数据集信息

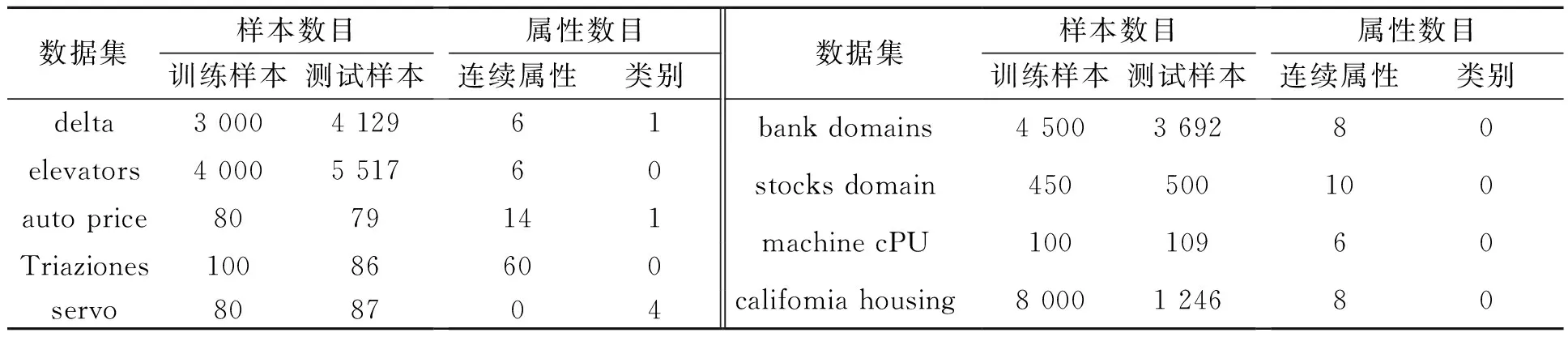
表2 分类数据集信息

Satimage通过已知的3×3像素的图像，对中心像素的类别进行预测.陆地卫星一次扫描结果(Landsat MSS imagery)包括4幅不同频谱图像，每幅图像包含2 340×3 380个像素.为了实验需要，每幅图像截取82×100像素构造Satimage数据集.构造方法是：将82×100像素划分为多个3×3像素的正方形，因每组图像共有4幅，因此可切出4个正方形，这4个正方形构造一条数据记录，显然数据维度是4×9=36．图像是矩阵形式，为便于计算，采用自上到下、自左向右的顺序将其矢量化(如图4所示).所求目标特征应该是第17、18、19、20维．若认为目标特征的类别仅与自己有关，那么可以直接采用第17、18、19、20维进行预测．若目标特征还和周围像素有关，则选择全部像素.笔者取用全部36维像素，该方法较普遍.数据共有6种类型：red soil、cotton crop、grey soil、damp grey soil、soil with vegetation stubble、very damp grey soil，分类目标是根据36维像素预测中心像素类型.

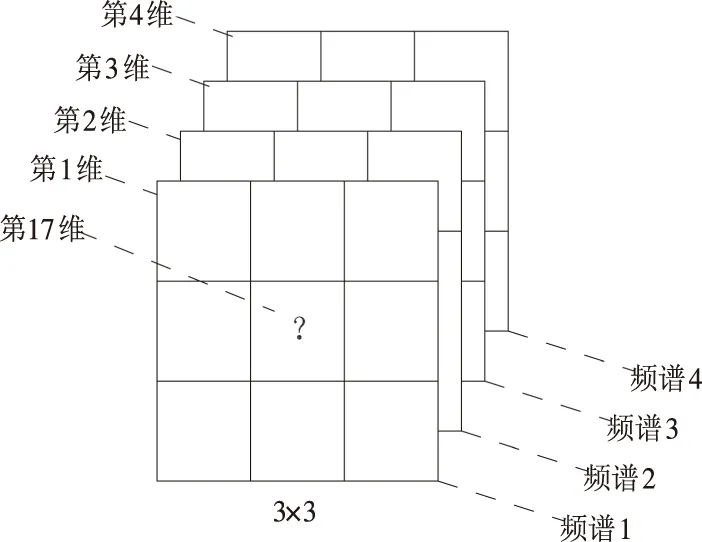
图4 Satimage 由36维像素预测中心像素类型

Shuttle根据飞行器所处的环境信息来判断飞机应选择人工降落或是自动降落(如图5所示).数据有9个属性，2个类别，58 000条样本．7个属性分别是time、stability、error、sign、wind、magnitude、visibilitya．7个类别分别是Auto(自动降落)和NoAuto(人工降落).80%的数据将选择人工降落(NoAuto)，其余为自动降落，因此默认的分类精度是80%，目标的精度是99%～99.9%.数据集以随机切割产生训练集(43 500个样本)和测试集(14 500个样本).

数据集IJCNN.给定一个长度为T=49 990的时间序列，序列中的每个样本都包含4个输入：x1(k)，…，x4(k)和一个输出y(k)．另外长度为91 701的时间序列用来测试．属性x1(k)表示与系统自然周期相关的二进制同步脉冲，为10位二进制形式，并以9个0，一个1的规模出现．属性x2(k)，x3(k)，x4(k)是[-1.5,1.5] 之间的实数，其中x4(k)和y(k)最为相关，因此后面构造特征时不仅考虑了x4(k)，还考虑了它的前后时刻的信息．我们采用文中的方法对时间序列行进行特征构造：x1(k)扩展为x1(k-5)，…，x1(k+4)等10个特征；x4(k)扩展为x4(k-5)，…，x4(k+4)等10个特征，x2(k)，x3(k)直接使用；最终形成22个特征.训练数据中90%的训练集为第1类，因此分类精度默认为90%，分类任务为构造模型已到达更高分类精度.

图5 Shuttle判断飞行器的降落方式

表3和4为不同算法的比较.对比表3、表4中4种算法在13个真实数据集的表现知，SparkELM算法在大部分数据集上的“Sigmoid”函数：g(x) = 1/(1+eλx)隐藏层初始节点都选取5个，每次递增5，并基于5-折交叉验证的方式选取最优个数，继而进行50次试验选取最优结果并取其平均值进行采集.对于SVM的核函数则选取径向基函数，并采用Hsu和Lin提出的排列组合方法选择最优的参数C和高斯核γ进行设置：C和γ的取值范围是C=[212,211,…,2-2],γ=[24,23,…,2-10]，共225种组合，对于每组(C，γ)进行50次随机试验，并对最优结果的平均值进行采集.实验数据被归一化到[0,1]之间，输出归一化到[-1,1].

4.2 训练时间与误差

BP、ELM和SparkELM的激励函数都选择分类及回归RMSE精度比BP、SVM有更好的泛化性能，并相较于ELM也有优秀表现.

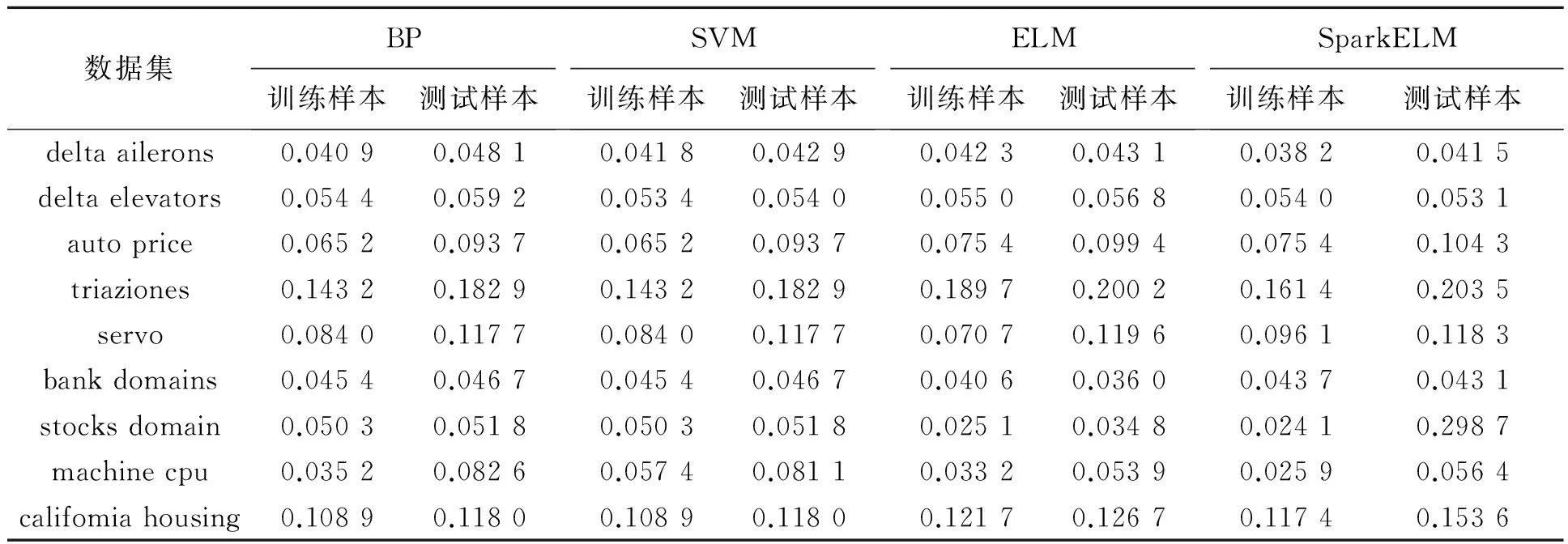
表3 4种不同算法的均方差(RMSE)

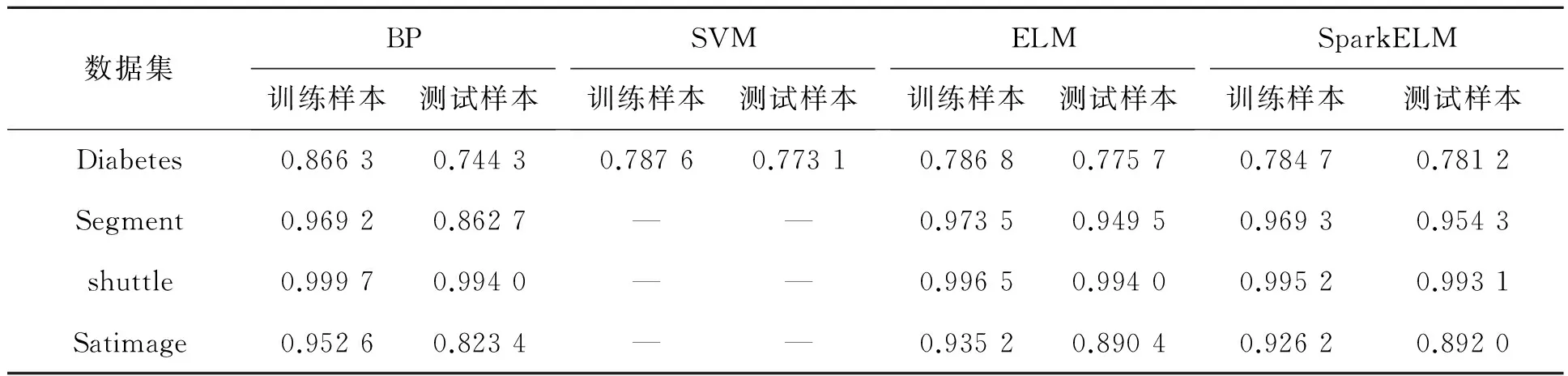
表4 4种算法在分类问题上的精度比较

4.3 不同参数下的性能变化分析

在Spark1.3.1中，reduce阶段，数据集的分片方式将直接影响算法性能，同时算法的最优分片数与群节点有很大联系，因此我们在数据集拥有不同节点数的情况下，调整数据分片数量，来进行并行性能测试.我们选择使用shuttle、ijcnn两个数据集进行试验，为保证结果的准确性，将所使用的shuttle数据增加至原始数据的100倍.集群的节点数由1个增加至6个，分片由1个增加至10个.为在不同节点情况下，不同分片数对算法产生的影响，首先控制每组实验的节点数不变，令分片个数逐渐增多，算法的执行时间如图6(a)～(f)所示.

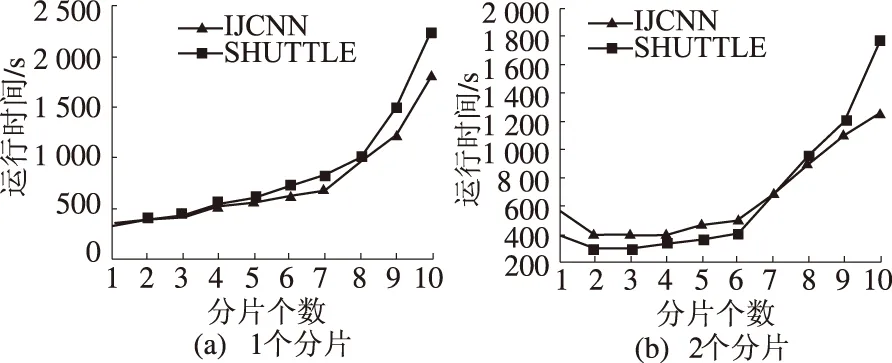
由图6(a)～(f)所示，在每组实验中保持集群节点个数不变，将分片由1个增加至10个，ELM算法训练时间都呈现先下降再逐渐攀升的趋势.训练时间首先随着分片的增多而逐渐减少，当分片数趋近于节点数的某个邻域范围时，训练时间达到最小值，而后随着分片数量的增多，算法的时间逐渐增加.呈现上述结果的主要原因是由于，ELM程序计算时间主要由mapPartitions与reduce两阶段的计算组成，当mapPartitions阶段完成后，需要将各从节点计算结果汇总至主节点进行reduce计算，因此算法除从节点和主节点计算用时外，还包括信息传递的通讯时间；在当前节点数不变得情况下，而随着分片数量的增加，当分片数趋近于节点数时，主节点得以最佳分片方式将数据集分发至各从节点进行运算，此时可保证在不需要额外通信开销的情况下，最大程度利用集群所有计算资源，并且由于分片个数趋近于节点个数，因此仅需要一个批次的数据传输即可完成分片结果至主节点的数据汇总，从而使通信开销降至最低；集群中所有从节点在分片个数等于节点个数时已被充分利用，因此在分片个数大于节点个数并逐渐呈现增长趋势时，某些集群将出现各节点数据分片分配不平均的情况，获取较多计算任务的从节点在进行额外任务的计算时，其他节点将出现停等现象，除此之外，数据汇总时由于该节点将产生额外的传输开销，因此ELM算法整体通信代价将逐渐增加，导致算法时间进一步提升，故而其所用时间也将呈增长趋势.

当数据集分片方式固定，集群节点个数对算法性能的影响可通过观察图7(a)～(f)可知：当提升集群从节点数量，集群节点逐渐趋近于分片个数时，主节点将计算任务重新分配，减少了各节点的平均任务数量及计算时间，提升了算法的整体并行性能，新添加节点提交任务所增加通信时间，相较于算法提升时间而言要小得多，该阶段ELM算法的整体性能随着节点增加将有所提升；当节点数大于分片个数并继续增加时，由于集群所有从节点已获得较为均匀的最小分片计算任务，其后所添加的节点并未使mapPartitions-reduce阶段的计算时间有所减少，反而增加了额外通信开销，整体而言，并未使ELM算法性能有所提升.

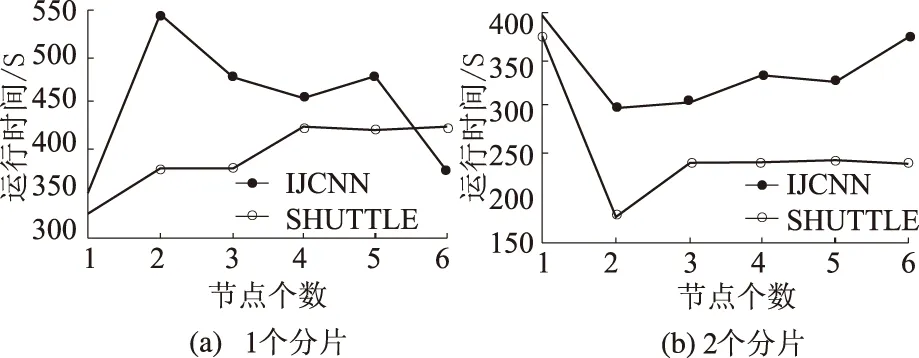
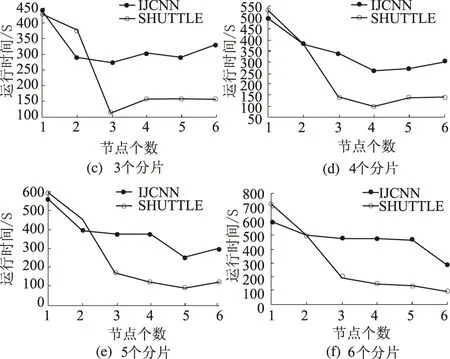
图7 分片固定时运行时间随节点个数变化情况

因此，节点个数接近于分片数时，ELM算法整体时间代价最小，性能最优.通常而言，集群在没有任务丢失的前提下，可以使ELM算法性能最为高效的分片个数P最佳≈节点个数s.

4.4 加速比

为评价SparkELM算法的加速性能，我们引入加速比S(n)对算法性能进行衡量，加速比的计算公式定义如下：

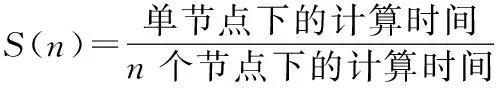
选取数据集IJCNN为例，并增加节点个数，将内核个数从4枚增加至24枚，为保证在节点个数不同时算法具有最优的运算性能，算法基于上述3.2节中论述的最优分片原则，将按照在当前节点最优分片区间对数据集进行划分，以保证ELM算法在当前集群的节点情况下具有最佳的并行性能.此外，为增加测试的数据规模，提升mapPartitions-reduce阶段运算时间的比重，减少通信消耗对计算的影响，实验中将原数据集IJCNN分别复制100倍、200倍、400倍和800倍作为训练集对ELM算法进行测试.4种情况表现如图8所示.

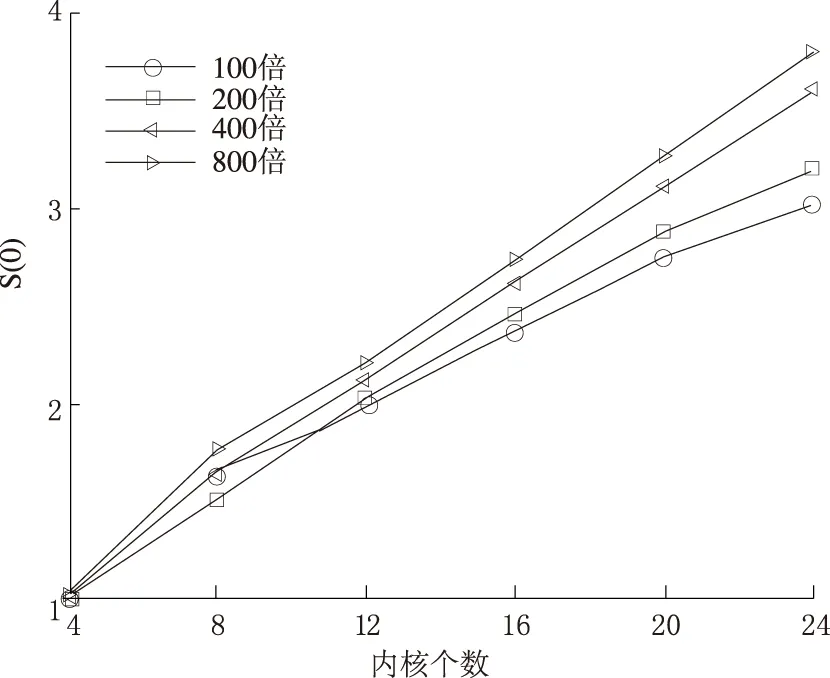
图8 最优分片下集群加速比

最优的并行化系统的加速效果应呈现线性增长特性，集群节点个数以n倍增长时，加速效果也保持n倍提升.但事实上，随着节点个数的增长，节点间通信代价也随着增大，加速效果难以呈现线性增长.正如图8中所示，随着数据规模增大，尤其当数据量极为庞大时，通信代价将被弱化，各节点的计算时间在总时间中将占较大比重，算法的加速效果也将趋于线性增长.结合具体情况，当数据规模较大时，以最优分片对数据集合进行划分，同时大规模提升集群的节点数量，可以使ELM算法的并行度呈线性提升.

5 结论与展望

ELM算法能解决回归及分类问题，并有训练速度快、泛化性能良好等特点，但在面对日益膨胀的大规模数据时仍亟待并行化扩展.本论文通过分析ELM的运算机制，基于Spark并行编程框架，设计并实现了并行SparkELM算法，实验表明，SparkELM算法不仅满足大数据量的计算需求，而且有良好的加速表现.在未来的工作中，我们将进一步对并行算法进行改进，以充分利用计算机资源.由于Spark 仍然在持续升级更新之中，因此使用API之前必须明确底层实现机制及版本差异，优化算法设计及实验.此外，不同于传统的同时支持规约操作和主从结构的交互式接口(如MPI)，Spark仅支持主从结构模式，需要两种交互模式相结合：主节点首先应分配任务，并将重要参数信息传递给从节点；从节点应将计算结果返回给主节点.因此应在设计上谨慎操作以减少算法在此种交互模式下开销，保证算法拥有最优性能，在后续开发中，我们将结合更高性能的Spark版本，对算法进行更新调整.

[1] HUANG G B,ZHU Q Y,SIEW C K.Extreme learning machin:Theory and applications[J]. Neu rocomputing，2006,70(1/3):489-501.

[2] HE Q,ZHUANG F Z,LIN J C,et al. Parallel implementation of classification algorithms based on mapreduce[C].//In Proceedings of Rough Sets and Knowledge Technology,2010 ,655-622.

[3] VERMA A,LORA X,GOLDBERG D E.,et al.Scaling genetic algorithms using mapreduce[J],In Proceedings of International Conference on Intelligent Systems Design and Applications,2009，13-18.

[4] HUANG G B,ZHOU H,DING X,et al.Extreme learning machine for regression and multiclass classification[J]. Syst Man Cybern Part B Cybern IEEE Trans,2012,42(42):513-529.

[5] CAO J, LIN Z, HUANG G B, et al .Voting based extreme learning machine[J]. Inf Sci ，2012，185(1):66-77.

[6] LIANG N Y,HUANG G B,SARATHANDRAN P,et al.A fast and accurate on-line sequential learning algorithm for feedforward networks[J]. IEEE Transactions on Neural Network,2010,17(6):1411-1423.

[7] SUN Z,LIN T,RISHE N,Large-scale matrix factorization using mapReduce[C]. In Proceedings of IEEE International Conference on Data Mining Workshops,2010，242-1248.

[8] ZAHARIA M,CHOWDHURY M,RANKLIN M J,et al.Spark：cluster computing with working sets[C] in Proceedings of the 2nd USENIX conference on Hot topics in cloud computing,2010.15(1):1765-1773.

[9] ODERSKY M,SPOON L,VENNERS B.Programming in Scala[M]. Artima,2008.

[10]ODERSKY M,ALTHERR P,CREMET V,et al.The Scala language specification[M]，2008.

[11]PANDA B,HERBACH J S,BASU S,et al.Planet:massively parallel learning of tree ensembles with mapreduce[C].//In:Proceedings of the 35th international conference on very large data bases,2009,2(2):1426-1437.

[12]CHU C T,SANG K K,LIN Y A,et al.Map-Reduce for machine learning on multicore[J].In Proceedings of Advances in Neural Information Processing Systems，2006(19):281-288.

[13]FAN R E,CHANG K W,HSIEH C J,et al.LIBLINEAR：A library for large linear classification[J] Journal of Machine Learning Research,2010,9(12):1871-1874.

[14]HE Q, SHANG T, ZHUANG F, et al, Parallel extreme learning machine for regression based on mapreduce[J] . Neurocomputing 102(2):52-58.

Sparked-based Parallel Extreme Learning Machine

DENG Wanyu, LI Li, NIU Huijuan

(School of Computing Science, Xi’an University of Posts and Telecommunications, Xi’an 710061, China)

With the rapid expansion of the scale of the data, stand-alone serial neural networks are faceing normous computational challenges. It is difficult to meet the expansion of real-world applications. In this paper, we proposed a parallel extreme learning machine (parallel ELM) algorithm based on Spark. By leveraging Spark parallel platform with efficient management mechanism and efficient matrix computations of large-scale data, the acceleration for solving ELM is achieved. The learning process of parallel ELM takes only one set of Map and Reduce operation to complete.The experimental results on a large number of real data sets show Spark-based parallel ELM algorithm can achieved a significant performance improvment compared with the serial ELM.

extreme learning machine; neural network; parallelization ELM algorithm; Spark

16-03-04；

2016-05-27

国家自然科学基金资助项目(61572399)；陕西省科技新星资助项目(2013KJXX-29)

邓万宇(1979—)，男，河南南阳人，西安邮电大学副教授，博士，主要从事数据挖掘、机器学习与知识服务研究，E-mail：58028654@qq.com．

1671-6833(2016)05-0047-10

TP389.1

A

10.3969/j.issn.1671-6833.2016.05.010