考虑含筋率影响的弯矩增大系数计算方法

林上顺，陈宝春

(1.福建工程学院 土木工程学院, 福建省土木工程新技术与信息化重点实验室,福建 福州 350118；2.福州大学 土木工程学院，福建 福州 350116)



考虑含筋率影响的弯矩增大系数计算方法

林上顺1，陈宝春2

(1.福建工程学院 土木工程学院, 福建省土木工程新技术与信息化重点实验室,福建 福州 350118；2.福州大学 土木工程学院，福建 福州 350116)

已有文献指出，钢筋混凝土偏压柱的弯矩增大系数与含筋率有关，而我国结构设计规范中弯矩增大系数的计算不考虑含筋率的影响.为此，在收集的33根试件资料基础上，结合所开展的有限元分析，进行了理论分析，同时开展有限元参数分析。结果表明：弯矩增大系数计算式中的曲率影响系数不仅与长细比、偏心率有关，还与含筋率有关；在长细比、偏心率相同的情况下，含筋率越大，弯矩增大系数越大.根据分析结果，提出了考虑含筋率影响的曲率影响系数计算公式，应用收集到的文献试件验证了公式的计算精度.

含筋率；弯矩增大系数；承载力；钢筋混凝土偏压柱

0 引言

偏心距为e0的钢筋混凝土偏压长柱，在轴力N作用下会产生横向挠度Δ，因此构件承担的实际弯矩为N(e0+Δ)，其值大于初始弯矩Ne0.实际弯矩与初始弯矩的比值常被称为弯矩增大系数或偏心增大系数，通常用η表示[1-3].

关于弯矩增大系数的计算方法，国内外已开展大量的研究.1977年，原国家建委建筑科学研究院建筑结构研究所指出：“含筋率对η是有影响的，因为配置的钢筋增加了柱的刚度，使η值减小”[2].我国1985版的公路钢筋混凝土及预应力混凝土桥涵设计规范(JTJ 023—85)[3]第4.1.19条规定，当构件全部纵向钢筋的配筋率大于3%时，混凝土截面惯性矩应乘以1.2.可见，在这个阶段，我国一些规范和文献普遍认为η随含筋率的增大而减小.

在我国现行的混凝土结构设计规范(GB 50010—2010)[4]与公路钢筋混凝土及预应力混凝土桥涵设计规范(JTG D62—2004)[5]、美国混凝土结构设计规范(ACI 318—05)中，弯矩增大系数仅考虑长细比、偏心率的影响，与含筋率无关[6-7]；然而，在欧洲混凝土结构设计规范(Eurocode 2：EN1992-1-1：2004)中，二阶弯矩的计算考虑了含筋率的影响[6-7].可见，在弯矩增大系数的计算方面，国内外规范并不一致，需要进一步开展系统深入的研究.

文献[8]在收集既有试件的基础上，进一步开展了14根钢筋混凝土偏压柱极限承载力试验，发现弯矩增大系数计算式中的曲率影响系数ζ不仅与长细比、偏心率有关，还与含筋率有关，且ζ的计算式对弯矩增大系数η的计算结果有较大影响[8].笔者在文献[8]研究的基础上，利用ANSYS通用软件提供的参数化设计语言(ADPL)等高级分析技术[9-10]，进一步开展有限元参数分析，对曲率影响系数的计算方法进行研究.

1 规范弯矩增大系数的计算

1.1 中国JTJ 023—85 规范公式

1985版公路桥涵设计规范(JTJ 023—85)第4.1.16条规定，弯矩增大系数计算式如式(1)[3]

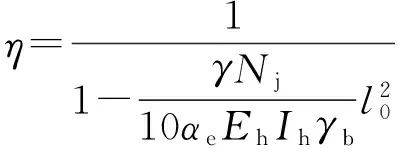
(1)

式中:Nj为计算纵向力；Eh为混凝土的弹性模量；Ih为混凝土截面的惯性矩；l0为压杆的计算长度；αe为与偏心有关的系数.γb为构件工作条件系数，取0.95；γc为材料安全系数，取1.25.

1.2 中国JTG D62—2004规范公式

JTG D62—2004规范中，弯矩增大系数计算如式(2)～式(4)[5]

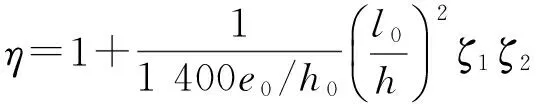
(2)

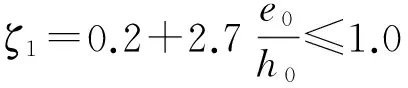
(3)

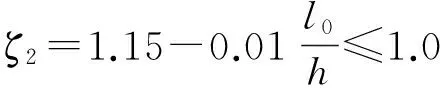
(4)

式中：e0为轴向力对截面重心轴的偏心距；h0为截面有效高度；h为截面高度；ζ1为荷载偏心率对截面曲率的影响系数；ζ2为构件长细比对截面曲率的影响系数.

1.3 中国GB 50010—2010规范公式

GB 50010—2010中的弯矩增大系数计算式见式(5)和式(6)[4]

(5)

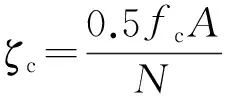
(6)

式中：M为弯矩设计值；ζc为偏心率对截面曲率的影响系数；fc为混凝土抗压强度设计值；A为构件横截面面积；ea为附加偏心距.

式(5)的公式源自GB 50010—2002中的弯矩增大系数计算式(与式(2)一致).根据GB 50010—2010的条文说明，该规范修订增加了500 MPa钢筋，截面的极限曲率有所增大，为便于计算，同时偏安全考虑，式(2)分母中的1 400改为1 300；在弯矩增大系数计算式中，取式(2)中的长细比对曲率的影响系数ζ2为1.0，偏心率对曲率的影响系数ζc与GB 50010—2002中的ζ1计算式相同.

1.4 美国ACI 318—05规范公式

与JTG D62—2004不同，美国规范(Building Code Requirements For Structural ConcreteACI 318—05)采用一阶弹性分析计算构件的弯矩，然后通过弯矩放大系数考虑二阶效应的影响，弯矩增大系数如式(7)～式(10)[6]所示

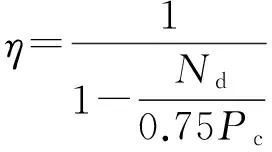
(7)

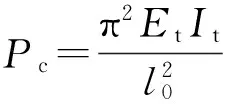
(8)

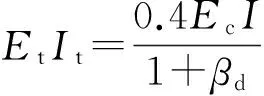
(9)

Ec=4 739f0.5ck.

(10)

式中：fck为混凝土轴心抗压强度标准值；βd为轴向持续荷载与总轴向荷载的比值；Ec为混凝土弹性模量.

1.5 欧洲EUROCODE 2规范公式

欧洲规范Eurocode 2：Design of Concrete Structures(EN 1992-1-1:2004)中，挠度Δ的计算采用基于名义曲率的简化方法.若轴力产生的附加弯矩为NdΔ，则考虑附加弯矩的总弯矩如式(11).挠度Δ的计算考虑了试件的含筋率、徐变系数等因素，如式(12)和式(13)[7]

M=M0+NΔ；

(11)

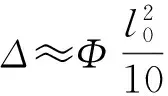
(12)

Φ=Φ0KrKΦ.

(13)式中：Φ为截面曲率；Φ0为极限曲率；Kr、Kφ为计算参数(与含筋率、长细比、混凝土强度等级等相关).

2 试件的弯矩增大系数计算分析

文献[8]指出，当试件的尺寸、材料以及长细比、偏心率确定时，试件的承载力随弯矩增大系数的确定而确定.反之，若已知试件的承载力，代入钢筋混凝土柱承载力公式，可反求试件的弯矩增大系数η′.可见，弯矩增大系数与试件的承载力一一对应.

2.1 试件资料介绍

文献[8]收集了大量的钢筋混凝土偏压试件的试验资料，这些试件的长细比和含筋率的统计详见该文献的表4.试件的边界条件为两端铰接；试验装置主要由台座、加载装置、测试仪表等组成；受压构件采用柱顶加载，如图1所示.

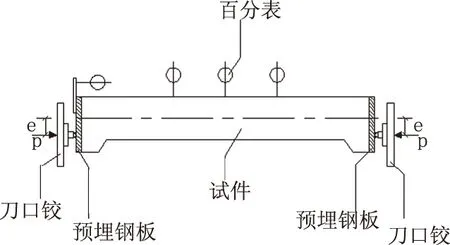
图1 混凝土偏压柱加载布置图[8]

文献[8]开展了14根钢筋混凝土偏压柱的极限承载力试验，各试件的参数详见该文献的表2.根据试件轴向和横向误差的测量结果，试件F4-3的横向偏差达到5 mm(往远加载侧)，在进行承载力计算时将横向误差值与设计的偏心距进行叠加，作为该试件的偏心距.

2.2 试件的试验值与规范计算值的比较

分别采用文献[8]提出的η′计算方法，以及JTG D62—2004、GB 50010—2010中的η计算公式，对文献[8]的表2、表4中长细比不小于15的试件进行计算.将η除以η′得到二者的比值，见图2、图3.

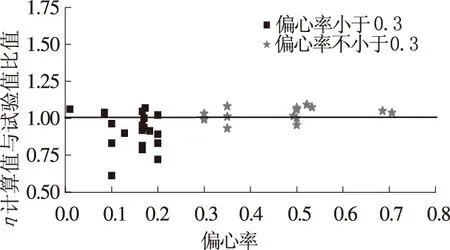
图2 η与η′的比值(JTG D62—2004)

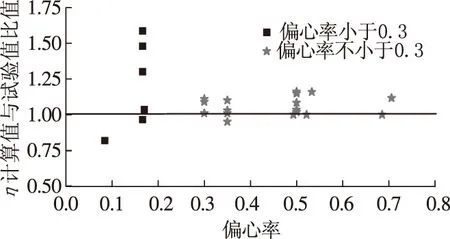
图3 η与η′的比值(GB 50010—2010)

从图2可以看出，对于偏心率小于0.3的试件，按JTG D62—2004计算的η大部分偏小；对于偏心率不小于0.3的试件，按JTG D62—2004计算的η大部分偏大.从图3可以看出，按GB 50010—2010计算的η大部分偏大，且部分试件偏大较多.

3 有限元参数分析

从文献[8]的有限元分析可知，采用有限元方法进行钢筋混凝土偏压柱的承载力计算具有足够的精度，可用于参数分析.

3.1 有限元参数分析

根据文献[8]的有限元计算结果与试验结果比较可知，二者比值的均值为0.984，方差为0.002，表明有限元计算方法具有较高的精度，可用于参数分析.笔者在相关研究的基础上，进一步开展有限元参数分析，对试验数据进行补充.在有限元参数分析中，试件的边界条件和加载方法与文献[8]的表2、表4中的试件完全相同.应用ANSYS程序计算试件的承载力.其中混凝土采用Solid65实体单元，混凝土的应力-应变关系与GB 50010—2002相同；钢筋采用Link8单元，钢筋的应力-应变关系曲线取理想弹塑性双折线曲线；柱端加载所用的钢垫板采用Solid45单元进行模拟.钢筋与混凝土之间采用分离式单元，假定钢筋与混凝土通过共用节点联结在一起，不考虑相对滑移，其有限元模型如图4(为体现钢筋与混凝土之间的粘结关系，仅示出钢筋混凝土柱的部分模型).计算时，采用增量法对模型进行加载，采用弧长法进行非线性问题的求解，并取偏压柱的荷载—位移曲线的峰值点所对应的荷载作为该柱的极限承载力.

图4 有限元模型

有限元参数分析中，钢筋混凝土柱的长细比取值为15.0、17.5、20.0、22.5、25.0、27.5、30.0，偏心率取值为0.05、0.10、0.15、0.20、0.25、0.30、0.35、0.40.有限元计算时，截面尺寸及截面形式与第一批试件一致.混凝土立方体强度为38.5 MPa，钢筋屈服强度为300 MPa，弹性模量为2.0×105MPa.

从工程实际看，钢筋混凝土偏压柱的单侧含筋率一般不大于2.0%，按照JTG D62—2004关于受压构件最小含筋率的规定，参数分析试件的单侧含筋率取0.251%、0.566%、1.005%、1.571%、1.901%，截面配筋方式为对称配筋，保护层厚度取20 mm.

3.2 弯矩增大系数变化规律分析

3.2.1 弯矩增大系数与长细比的关系

图5(a)～图5(c)给出了含筋率为0.251%、1.005%、1.901%的钢筋混凝土柱，其η随长细比的变化规律.由图5可见，钢筋混凝土柱的η随长细比的增大而增大；在长细比相同情况下，偏心率越大，η越小；η与长细比的关系接近于直线，其斜率随着偏心率的增大而减小；当长细比为15时，η随偏心率的变化幅度相对较小，随着长细比增大，η随偏心率的变化幅度逐渐增大；不同含筋率的钢筋混凝土柱的η随长细比的变化趋势均相同，但变化幅度并不一致.

3.2.2 弯矩增大系数与偏心率的关系

图6给出了长细比为15、20、25、30的钢筋混凝土柱，在含筋率为0.251%、1.005%、1.901%的情况下，其η随偏心率的变化规律.由图6可见，含筋率变化时，钢筋混凝土柱的η均随偏心率的增大而减小，当偏心率小于0.3时，η随偏心率的变化幅度较大；当偏心率不小于0.3时，η随偏心率的变化幅度较小；在各种含筋率情况下，若偏心率相同，η均随长细比的增大而增大；在相同的长细比与偏心率情况下，不同含筋率所对应的η有所差异.

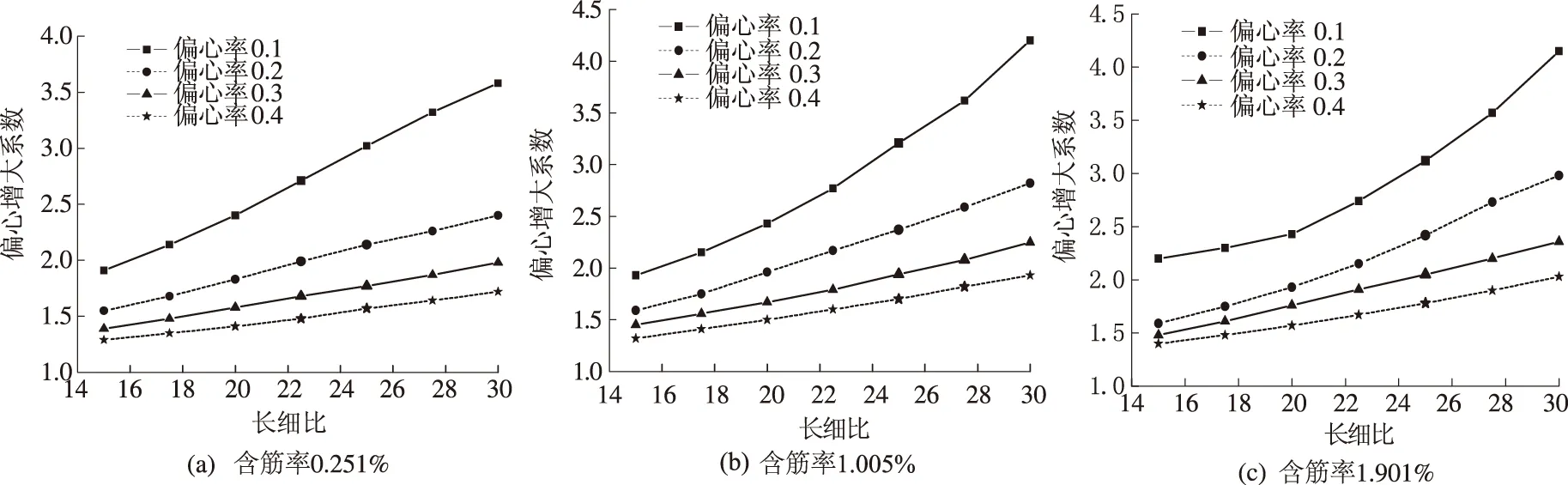
图5 弯矩增大系数与长细比的关系

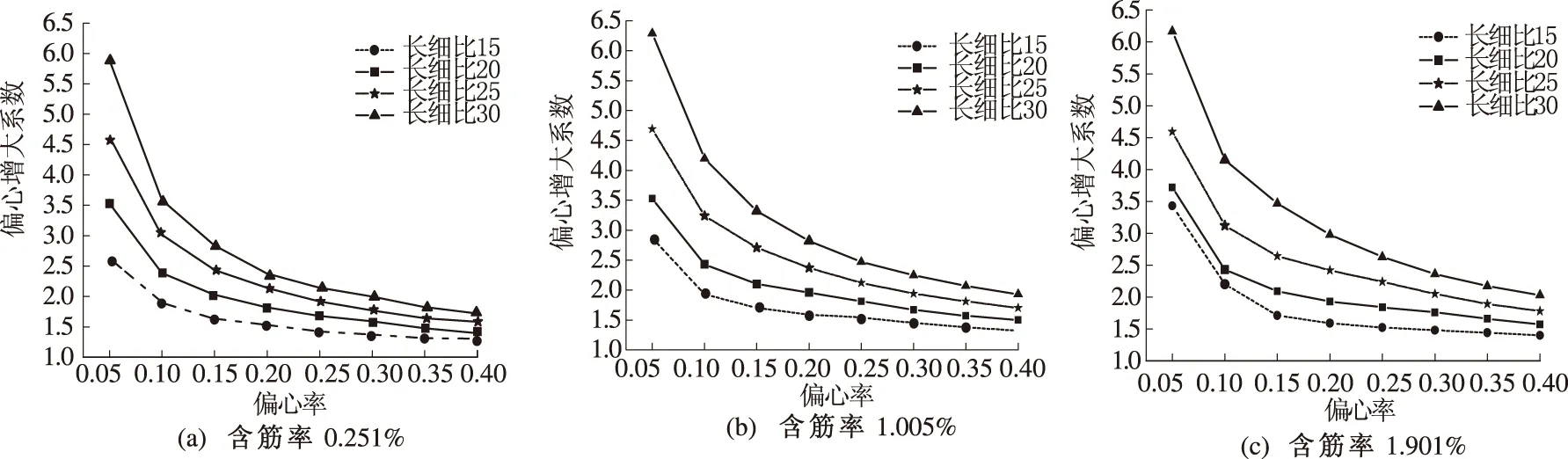
图6 弯矩增大系数与偏心率的关系

3.2.3 弯矩增大系数与含筋率的关系

图7分别给出了长细比为15、20、25、30的钢筋混凝土柱，在偏心率为0.1、0.2、0.3情况下，其η随含筋率的变化规律.从图7可见，在相同的含筋率情况下，η随长细比的增大而增大；偏心率越大，η随长细比的变化幅度越小.

从图7还可以看出，当钢筋混凝土柱的长细比达到30且含筋率不大于1.0%时，η随含筋率的变化幅度相对较大；当含筋率大于1.0%时，η随含筋率的变化幅度相对较小.

3.3 包括含筋率参数的弯矩增大系数计算公式

文献[6]推导了弯矩增大系数的计算式，如式(2)所示.在推导过程中，混凝土极限应变εcu取0.003 3，长期荷载作用下的压应变增大系数

Ky取为1.25.对于试件，应不考虑长期荷载的影响，此时Ky应取为1.0，式(2)改写为式(14)

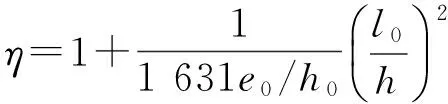
(14)

式(14)没有考虑含筋率的影响，但从本文第3节的有限元参数分析结果可见，含筋率对弯矩增大系数有一定的影响.因此，笔者将式(14)中的曲率影响系数ζ表达为式(15)的形式

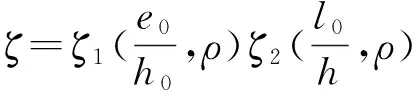
(15)

式中：ρ为截面单侧含筋率.

根据第3节的分析，当偏心率小于0.3时，弯矩增大系数随偏心率的变化幅度较大；当偏心率不小于0.3时，弯矩增大系数随偏心率的变化幅度较小.因此，以偏心率0.3为界，分别进行分析.

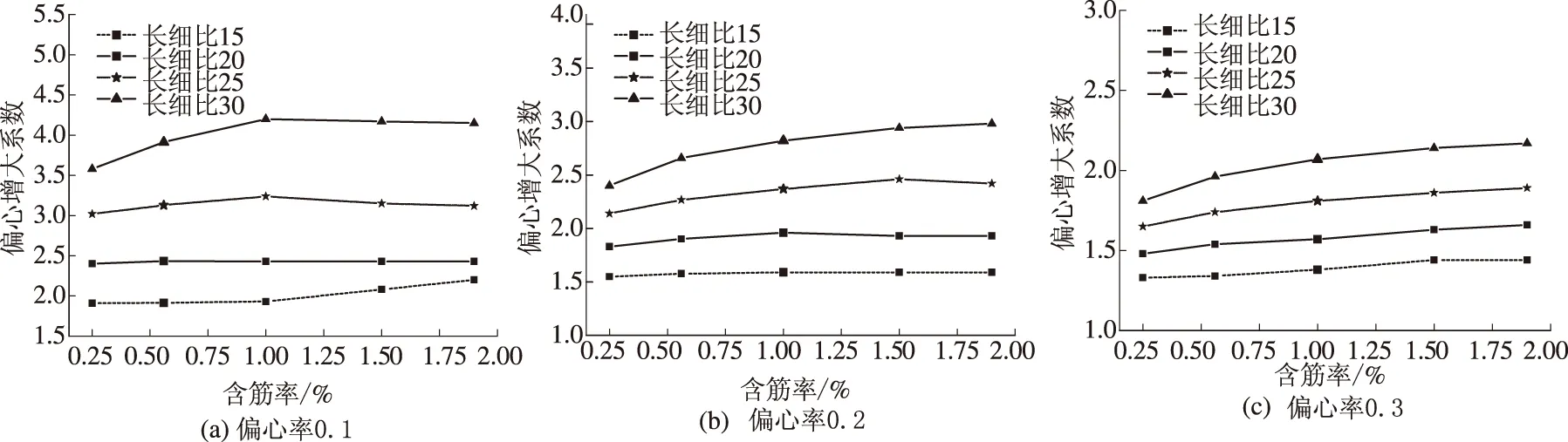
图7 弯矩增大系数与含筋率的关系

3.3.1 偏心率不小于0.3的钢筋混凝土柱

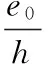
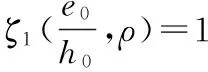
(16)

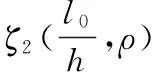
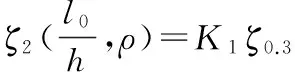
(17)

K1=0.078(100ρ)+0.851；

(18)

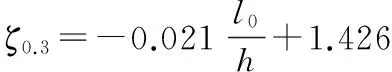
(19)

3.3.2 偏心率小于0.3的钢筋混凝土柱

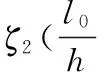
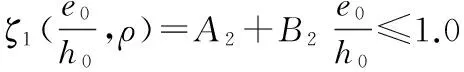
(20)

A2=0.049(100ρ)2-0.213(100ρ)+0.785；

(21)

B2=-0.251(100ρ)2+0.877(100ρ)+0.774.

(22)

3.4 考虑含筋率影响的计算公式的精度分析

图8为不同计算结果与实验值之比.按3.3节提出的计算公式对文献[8]的表2、表4中的试件进行承载力计算.笔者公式的计算结果与试验值比值见图8(a)，其均值为0.977，方差为0.005；仅少量试件的计算结果大于试验值，最大偏差仅为12.8%.可见，笔者提出的拟合公式具有较高的计算精度.

按GB 50010—2010计算方法对文献[8]的表2、表4中的试件进行承载力计算，计算结果与试验值的比值见图8(b).从图8(b)可见，当试件的长细比大于21时，所有试件的计算结果均小于试验值，且偏低较多，可见GB 50010—2010的计算方法较为保守.

按JTG D62—2004的方法对文献[8]的表2、表4中的试件进行承载力计算，其计算结果与试验值的比值见图8(c)，可见较多试件的承载力计算值大于试验值，偏于不安全.

(a)笔者公式的计算结果与试验值 (b)GB 50010—2010计算结果与试验值 (c)JTG D62—2004计算结果与试验值

图8 计算结果与试验值比较

Fig.8 The ratio of the calculation results to experimentd results

3.5 讨论

JTJ 023—85规范中弯矩增大系数的计算采用刚度表达式.该规范在计算偏压柱的刚度时，考虑了钢筋对截面刚度的贡献，因此根据含筋率对混凝土截面的惯性矩进行适当放大，其结果是含筋率越高，弯矩增大系数越小.在现行的规范中，弯矩增大系数的计算采用曲率表达式，即通过计算钢筋混凝土偏压柱的极限曲率和曲率影响系数，然后进一步计算其弯矩增大系数.因此，旧版规范的弯矩增大系数与构件刚度密切相关；而现行规范的弯矩增大系数与构件的极限曲率密切相关.

图8(a)中钢筋混凝土柱的承载力计算，其弯矩增大系数计算式中的曲率影响系数均考虑了含筋率的影响；而图8(b)和图8(c)中钢筋混凝土柱的承载力计算，分别采用GB50010—2010规范和JTG—2004规范的公式，其弯矩增大系数计算式中的曲率影响系数不考虑含筋率的影响，其计算结果与试验结果存在一些偏差.计算误差的根源在于曲率影响系数的计算不够合理，从而导致弯矩增大系数的计算误差，并影响了钢筋混凝土偏压柱承载力计算结果的精度.

4 结论

钢筋混凝土偏压柱的试验和有限元参数分析表明，曲率影响系数不仅与偏心率和长细比有关，还受到含筋率的影响；在笔者的参数分析范围内，含筋率越大的偏压柱，其弯矩增大系数越大.

笔者提出的包括含筋率参数的曲率影响系数计算式，对规范的弯矩增大系数计算式进行了修正，其计算精度比现有的不考虑此影响的我国规范计算方法有所提高.式(14)的弯矩增大系数计算式适用于钢筋混凝土偏压试件的承载力计算，然而在实际工程中，钢筋混凝土压弯构件在长期荷载作用下的极限压应变可能大于试件，还可能由于施工误差存在附加的偏心距，所有这些因素均将导致其弯矩增大系数大于短期荷载作用下的试件，因此，弯矩增大系数的计算是一个复杂的问题，还有待进一步研究.

[1] 顾祥林. 混凝土结构基本原理[M]. 上海：同济大学出版社，2004.

[2] 国家建委建筑科学研究院建筑结构研究所. 钢筋混凝土偏心受压构件的纵向弯曲[C]//钢筋混凝土结构研究报告选集. 北京：中国建筑工业出版社，1977:182-200.

[3] 中华人民共和国交通部.JTJ023—85公路钢筋混凝土及预应力混凝土桥涵设计规范[S] . 北京: 人民交通出版社,1985.

[4] 中华人民共和国建设部.GB50010—2010混凝土结构设计规范[S]. 北京: 中国建筑工业出版社，2010.

[5] 中华人民共和国交通部.JTGD62—2004公路钢筋混凝土及预应力混凝土桥涵设计规范 [S]. 北京: 人民交通出版社, 2004.

[6] 贡金鑫，魏巍巍，胡家顺. 中美欧混凝土结构设计[M]. 北京: 中国建筑工业出版社, 2007.

[7]EuropeanCommitteeforStandardization.Eurocode2：DesignofConcreteStructures(EN1992-1-1:2004) [S],Lausanne：ElservierSciencePublishers, 2004.

[8] 陈宝春, 林上顺. 钢筋混凝土偏压柱承载力计算中的曲率影响系数[J]. 建筑结构学报,2014,35(3)：156-163.

[9] 韩艳, 陈政清, 李开言. 在ANSYS中实现双肢薄壁桥墩参数优化设计的方法[J]. 铁道科学与工程学报, 2005, 2(6)：15-18.

[10]刘世忠, 刘永健, 程高，等. 公路桥梁车桥耦合振动数值分析方法[J]. 郑州大学学报 (工学版), 2014, 35(1)：94-98.

[11]陈旭，周东华，韩春秀，等. 钢筋混凝土柱稳定问题的图算法[J].工程力学, 2014, 32(10)：106-113.

Calculation Method of Moment Enlargement Coefficient Considering Effect of Reinforcement Ratio

LIN Shangshun1,CHEN Baochun2

(1.Fujian Provincial Key Laboratory of Advanced Technology and Informatization in Civil Engineering,College of Civil Engineering, Fujian University of Engineering, Fuzhou, Fuzhou 350118, China；2. College of Civil Engineering, Fuzhou University, Fujian 350116, China)

It is pointed out that moment enlargement coefficient of eccentrically loaded reinforced concrete column is related with reinforcement ratio which is not yet considered by China structural design specification. Therefore, based on 33 specimen test data from references and load-bearing capacity tests of 14 eccentrically-loaded reinforced concrete columns, theoretical and FEM parametric analysis were carried out. Results show that the curvature influence coefficient in the calculation formula of moment enlargement coefficient is not only related with slenderness ratio and eccentricity, but also with reinforcement ratio. Bending moment enlargement coefficient increases with reinforcement ratio under the condition of constant slenderness ratio and eccentricity. A calculation formula of curvature influence coefficient considering the effect of reinforcement ratio is put forward with its accuracy verified by specimen data from published papers.

reinforcement ratio；bending moment enlargement coefficient; load-carrying capacity; eccentrically loaded reinforced concrete column

2016-01-18；

2016-04-30

国家自然科学基金资助项目(U1305245)

林上顺(1972—)，男，福建永泰人，福建工程学院高级工程师，博士，从事桥梁结构研究，E-mail：midas2008@126.com.

1671-6833(2016)05-0033-06

TU318

A

10.3969/j.issn.1671-6833.2016.05.007