端部质量对有无损伤悬臂梁的模态影响分析

闫安志，陶天增，张振华

(1.河南理工大学 土木工程学院，河南 焦作 454000； 2.大连理工大学 工程力学系，辽宁 大连 116000)



端部质量对有无损伤悬臂梁的模态影响分析

闫安志1，陶天增2，张振华1

(1.河南理工大学 土木工程学院，河南 焦作 454000； 2.大连理工大学 工程力学系，辽宁 大连 116000)

工程实际中许多结构可简化为端部带有集中质量的悬臂梁，笔者通过数值模拟软件建立了端部带有集中质量的悬臂梁有限元模型，并进行了模态分析.研究了端部集中质量的改变对悬臂梁固有频率的影响，同时建立带有I型裂纹的悬臂梁(端部带有集中质量与不带有集中质量两种)模型，改变裂纹的位置和深度，研究了裂纹深度和裂纹位置对悬臂梁的频率变化规律.通过对比发现，裂纹越靠近端部对梁的频率影响越小，集中质量对带有裂纹悬臂梁固有频率有一定的影响.

悬臂梁；端部集中质量；转动惯量；裂纹；有限元

0 引言

工程实际中很多结构可简化为端部带有集中质量的悬臂式结构，例如端部带有发动机的飞机机翼，大型吊车，大型悬索大桥，悬臂挑梁，共振式破碎机等，并且生活中的悬臂梁大部分都为柔性悬臂梁(梁长/梁高>5).此类结构都可简化为端部带有集中质量的悬臂梁(CBCM，cantilever beam with concentrated mass on its free end)来研究，对于此类结构关注更多的是其振型和频率等.陆海桃等[1]通过试验和数值模拟研究了集中质量对悬臂梁振动模态的影响，文中只考虑了质量大小对悬臂梁频率的影响.王栋等[2]对附带有集中质量的转动惯量梁做了相关的理论分析，并建立了梁—质量系统的频率特征方程.Wang等[3]根据达朗贝尔原理将悬臂梁自由端的集中质量等效为惯性力和惯性力矩来研究其动力特性.Mousavi[4]和Abramovich[5]分别对带有端部集中质量的欧拉梁和铁木辛柯梁进行了动力学研究.吴泽玉[6]对于振型的构件位移分解及规律进行了研究.

结构中的裂纹是结构安全性的一大隐患.初始裂纹可能是制造缺陷或长期使用过程中由于过载或材料疲劳而产生的，柔性结构一般对所处的工作环境也比较敏感，所以柔性结构产生物理缺陷的几率比较大[7].研究不同端部质量情况下，不同位置的裂缝、不同深度的裂缝对悬臂梁固有属性的影响，具有良好的代表性.裂纹对悬臂梁振动频率的影响，王璋奇[8]、江凡[9]通过理论假设建立了含有裂纹的悬臂梁的振动微分方程，并进行了求解，得出了特征方程.Morassl[10]、沈亚鹏[11]、赵彬[12]、刘文光[13]从理论方面研究了单裂纹、多裂纹对悬臂梁振动的影响以及振动与疲劳耦合分析.葛永庆[14]通过数值模拟研究了裂纹参数对叶片静频、动频的影响.

为了更加贴近工程实际，笔者以工程中常见的CBCM为研究对象，建立了CBCM有限元模型，分析了考虑和不考虑集中质量转动惯量对CBCM的弯曲和扭转频率的影响，以及CBCM在有裂纹发生时，CBCM的频率变化规律.

1 端部带有集中质量的悬臂梁有限元模型以及理论计算

振动工程中常用两种梁模型：欧拉—伯努利梁和铁木辛柯梁.其中，欧拉—伯努利梁只考虑弯曲变形，铁木辛柯梁既考虑弯曲变形又考虑转动惯量和剪切变形.由文献[15]可知，CBCM的特征方程为：

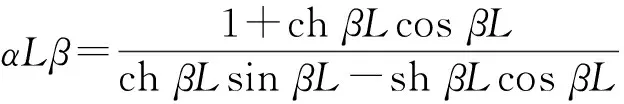
式中：M/ρAL=α，α的物理意义为附加质量与梁质量之比；ρ为梁的密度；A为梁的横截面积；L为梁的长度.β4=Mω2/EIαL，ω为梁的固有频率；E为弹性模量；I为梁的转动惯量.

在ANSYS中既支持自定义梁截面又基于铁木辛柯梁的梁单元是Beam188和Beam189.笔者取工字钢(GB 706—88)梁，型号32a，梁长取2 m，采用Beam189，将悬臂梁划分为100个单元，采用Mass21质量点单元代替梁端部集中质量.悬臂梁模型如图1所示.

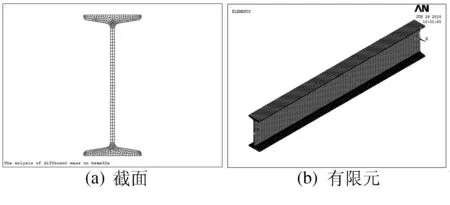
图1 工字钢截面和钢梁有限元模型

2 模态分析

模态是结构的一种固有振动特性，是一种研究结构动力特性的方法.通过ANSYS对其进行模态分析，可得到悬臂梁的前六阶模态如图2所示.

图2 端部带有集中质量的悬臂梁前六阶模态

为了研究集中质量对悬臂梁频率的影响，利用ANSYS的Block Lanczos算法，得到梁各阶频率随质量比的变化规律，如图3(a)所示.

为了模拟端部较大质量对弯曲振动的影响，利用mass21单元的参数特性，将端部质量假定为一密度为7 850 kg/m3的球体，仅考虑球体的质量及其绕梁轴线的转动惯量的影响，忽略球体半径的影响，梁固有频率随质量比的变化规律，如图3(b)所示.

从图3(a)可知，一阶绕弱轴弯曲、一阶绕强轴弯曲和二阶绕弱轴弯曲频率随α的增大而减小.当α为0.96时，一阶绕弱轴和一阶绕强轴弯曲频率变化最大，分别减小55%和54%；但是，二阶绕弱轴弯曲频率，仅减小17%.然而，一阶、二阶和三阶扭转频率却不受集中质量变化的影响，原因是集中质量单元加在了轴线的端部中心节点，并且忽略了集中质量的转动惯量.

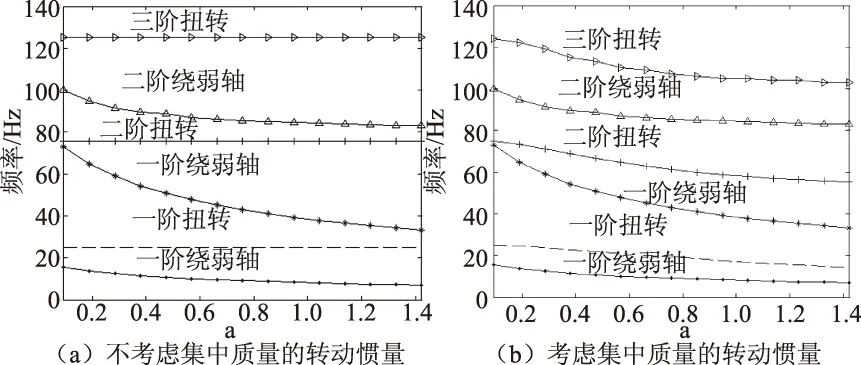
图3 悬臂梁固有频率随质量比的变化

从图3(a)和(b)对比可知，当考虑集中质量的转动惯量时，梁的一阶绕弱轴、一阶绕强轴和二阶绕弱轴弯曲频率随质量比的变化规律与不考虑集中质量转动惯量时相同；其前三阶扭转频率随增大而减小.当为0.96时，一阶、二阶和三阶扭转频率分别减小了43%、26%和17%.

3 裂纹对CBCM的频率变化

选取长2 m，CBCM端部集中质量为30 kg(α为0.19)和无集中质量的梁作为计算模型.研究7个不同位置裂缝及同一位置上不同深度裂缝对悬臂梁固有频率的影响，同时研究质量比α(不考其转动惯量)对有裂纹时的悬臂梁固有频率的影响.笔者在距离梁固定端0、0.3、0.6、0.9、1.2、1.5和1.8 m处，分别生成裂缝深度为5、10、20、30、40、50和60 mm的7组模型.在计算中，由于循环地运行ANSYS，为了节约时间，编制MATLAB程序调用ANSYS进行计算[16-17].

采用solid95单元建立带有裂缝的悬臂梁.由于裂缝的形状对梁的振动频率没有明显的影响[18]，故而为了方便，采用I型裂纹.有裂纹的悬臂梁模型如图4(a)所示，裂纹细节如图4(b)所示.

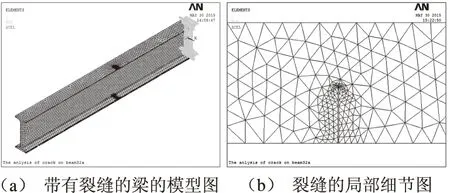
图4 带有裂缝的梁模型及裂缝局部图

为了对比研究裂缝的位置和深度对悬臂梁振动特性的影响，表1给出了CBCM和无集中质量的悬臂梁模型在无裂缝情况下的前六阶固有频率.笔者将具有相同深度但裂缝位置变化的悬臂梁模型编为一组，每组有7种裂缝位置不同的梁，共7组.这7组悬臂梁的前六阶固有频率随裂缝位置变化的情况，如图5所示.由图5可知，悬臂梁的各阶固有频率随裂缝位置的变化基本一致，距离固定端越远影响越小.有集中质量时，仅仅使得梁的频率数值相应减小.

表1 无物理缺陷(裂缝深度为0 mm)的悬臂梁前六阶频率

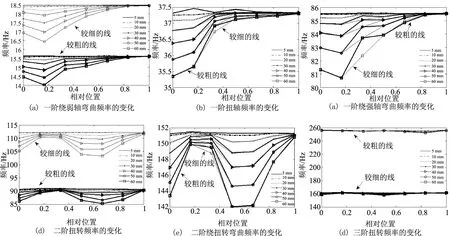
注：较细线表示无集中质量，较粗线表示CBCM梁

裂缝深度对CBCM的影响：将具体的频率值与表1中的数据进行比较，当裂缝深度为5 mm、10 mm时对梁的各阶频率影响很小，其中5 mm深裂缝对于一阶扭转频率几乎没有影响，10 mm深度裂缝对于各阶频率影响也比较小.当裂缝深度大于10 mm时，影响很明显，其中60 mm深度裂缝对各阶的频率影响都很大，例如在二阶绕弱轴弯曲频率中，频率差值最大达到8 Hz.

裂缝位置对CBCM的影响：将具体的频率值与表1中的数据进行比较，0 mm处出现裂缝，对一阶扭转频率影响最大；300 mm处(梁的3/20处)出现裂缝时，对一阶绕弱轴、一阶绕强轴弯曲频率影响最大；900 mm处(梁的9/20处)出现裂缝时，对二阶绕弱轴弯曲、三阶扭转频率影响最大；1 200 mm处(梁的3/5处)，对二阶扭转、二阶绕弱轴弯曲频率影响最大.频率变化的原因是由裂缝位置和固有振型节点(线)的远离程度决定的.在振型节点附近出现裂纹对该阶频率影响很小，而在振型腹点处出现裂纹，则对振型所对应的频率影响很大.且裂纹越深，梁的频率越低，说明裂缝的出现降低了梁的刚度.在前五阶频率中，频率大致都收敛到一点处，也即出现在1 800 mm处(梁的9/10处)的裂缝对梁的前五阶频率影响非常小.

考虑端部集中质量对有裂纹悬臂梁的影响时，一阶绕弱轴弯曲、二阶扭转、三阶扭转频率，整体上与不考虑集中质量时的规律一样，但是其整体上比不考虑集中质量时小.

4 结论

通过对CBCM梁的建模和模态分析，得到如下有结论：

(1)随着悬臂梁端部集中质量的增加，梁的各阶弯曲频率相应减小.当端部质量较小时，可以不考虑集中质量的转动惯量对扭转频率的影响.

(2)当端部质量较大时，必须考虑集中质量的转动惯量影响.随着悬臂梁端部集中质量的增加，梁的各阶弯曲频率和扭转频率相应减小.

(3)裂纹深度和位置对悬臂梁频率影响很大，裂纹位置对悬臂梁不同阶振型对应的频率影响规律各不相同，裂纹深度越大，梁固有频率越低.同时端部有集中质量时，对各阶固有频率的影响规律各不相同.

[1] 陆海桃, 仝艳文. 集中质量对悬臂梁振动模态影响的分析研究[J]. 装备制造技, 2014 (10) :122-124.

[2] 王栋. 附带有考虑集中质量的转动惯性的梁固有振动分析[J]. 振动与冲击,2010(29):221-225.

[3] WANG H,MENG Q,FENG W.Discussion of the improved methods for analyzing a cantilever beam carrying a tip-mass under base excitation [J]. Shock & Vibration,2014,20(1):153-160

[4] MOUSAVI S A,HEPPLER G R Comments on ‘natural frequencies of a uniform cantilever with a tip mass slender in the axial direction’ [J]. Journal of Sound and Vibration, 2012, 331(12): 2964-2968.

[5] ABRAMOVICH H,HAMBURGER O.Vibration of a cantilever timoshenko beam with a tip mass [J]. Journal of Sound and Vibration, 1991, 148(1): 162-170.

[6] 吴泽玉, 王栋炜, 汪志昊. 基于振型的构件位移分解及规律研究[J]. 郑州大学学报(工学版), 2015,36(5): 68-72.

[7] 李济泽. 具有裂缝的柔性悬臂梁的振动特性研究[D]. 福建: 福州大学机械工程系，2003.

[8] 王璋奇, 贾建援. 悬臂梁裂纹参数的识别方法[J]. 机械强度, 2002, 24(2):225-279.

[9] 江凡, 薛冬新, 宋希庚. 裂纹悬臂梁的扭转弹簧模型及其实验验证[J]. 振动、测试与诊断, 2004,24(2):143-145.

[10]ANTONINO M.Crack-induced changes in eigenparameters of beam structures [J]. Journal of Engineering Mechanics, 1993, 119 (9):1798-1803.

[11]沈亚鹏, 唐照千. 裂纹对悬臂梁板振动频谱的影响[J]. 固体力学学报, 1982, 2:247-251.

[12]张佳文, 赵彬. 含多裂纹悬臂梁的振动分析[J]. 湖南城市学院学报(自然科学版), 2009, 18(3):1-4.

[13]刘文光, 陈国平. 含裂纹悬臂梁的振动与疲劳耦合分析[J]. 振动与冲击, 2011, 30(5):140-144.

[14]葛永庆, 安连锁. 裂纹参数对叶片固有频率影响的研究[J]. 动力工程, 2008,28(4):519-522.

[15]张义民. 机械振动[M]. 北京:清华大学出版社. 2007.3

[16]李朔东，马纲. 基于ANSYS的模态分析二次开发及应用[J]. 航天制造技术, 2004, 10：8-11.

[17]宋宏伟，刘浩. 基于 MATLAB 与 ANSYS 的结构优化设计[J]. 大连民族学院学报, 2011, 13(3):284-287.

[18]张利民, 王克明, 吴志广. 叶片模态分析的单元类型选择[J]. 沈阳航空航天大学学报, 2011,28(2):21-24.

The Mode Analysis of the Cantilever Beam with Concentrated Mass on Its Free End in the Case of Damage and No Damage

YAN Anzhi1， TAO Tianzeng2， ZHANG Zhenhua1

(1.School of Civil Engineering, Henan Polytechnic University, Jiaozuo 454000, China; 2.Department of Mechanics, Dalian University of Technology, Dalian 116000, China)

Many structures in the engineering, which can be simplified as cantilever beam with concentrated mass on its free end. The finite element model of the cantilever beam with concentrated mass on its free end is established, and the mode analysis of it is carried out in this paper. The effect on the natural frequency of the CBCM in the case of the mass change is studied. At the same time, a kind of cantilever beam model with I shaped crack is established. This kind of model includes two models: the free end of the beam with and without concentrated mass. Changing the position and depth of the crack, it can be found that the frequency of the beam is affected mostly by the crack depth. And the position of crack is closer to its free end of the beam, the influence of frequency of the beam is smaller. By comparison, it can be found that the lumped mass have a certain effect on the natural frequency of cracked cantilever beam. This research has certain guiding significance to optimization design、damage detection、maintenance of the cantilever beam with concentrated mass on its free end.

cantilever beam; concentrated mass；moment of inertia；crack; finite element method

2016-02-30；

2016-05-19

国家自然科学基金资助项目(51308195)；河南省科技厅科技攻关项目(132102210252)

闫安志(1965—)，男，河南人，河南理工大学教授，博士，主要从事结构振动控制研究，E-mail：yanzhi@hpu.edu.cn．

1671-6833(2016)05-0039-04

TB123

A

10.13705/j.issn.1671-6833.2016.05.008