基于MATLAB的汽车线性最优控制主动悬架仿真研究

刘本学，蔺超云，郭沛东，栗良玉

(郑州大学 机械工程学院，河南 郑州450001)



基于MATLAB的汽车线性最优控制主动悬架仿真研究

刘本学，蔺超云，郭沛东，栗良玉

(郑州大学 机械工程学院，河南 郑州450001)

为了论证主动悬架在改善汽车行驶平顺性方面的优越性，在建立车辆1/4主动悬架模型和随机路面激励模型的基础上，采用线性最优控制作为主动悬架的控制策略，并设计线性最优控制器，利用MATLAB建立频域和时域的主动悬架仿真模型，在随机路面激励上对主动悬架分别在频域和时域内进行仿真并与被动悬架进行对比分析.结果表明：主动悬架能够有效降低车身加速度、轮胎动载荷和悬架动挠度，从而显著提高汽车的行驶平顺性和操纵稳定性.该设计的模型建立、最优设计和仿真分析为主动悬架的进一步研究及实际应用提供了有益参考.

汽车；主动悬架；线性最优控制；平顺性

0 引言

为了提高主动悬架的性能，使汽车获得良好的行驶平顺性和操纵稳定性，国内外学者在主动悬架控制策略设计方面做了大量的研究：Kashani、Nagai Magao、Watanabe等[1-3]在模糊控制、神经网络控制等现代控制理论方面做了突出贡献；国内从上世纪80年代中期，以何渝生、胡海岩、丁科[4-6]为代表的学者开始了这方面的研究工作.

近几年，多数国内外研究都是采用现代控制理论基于两自由度车辆模型开展的，但激励是通过座椅传递给人的，为了更多地考虑人乘坐舒适性，笔者是在两自由度的车辆模型的基础上建立1/4车辆三自由度振动模型，应用线性最优控制理论，对主动悬架的性能开展仿真研究.

1 基于线性最优控制的主动悬架模型建立

1.1 主动悬架1/4车辆模型

由于笔者侧重悬架系统控制策略的研究，1/4车辆模型恰好能体现汽车的垂直振动特点，而三质量车辆模型能够体现人体对振动的敏感程度与路面不平度的关系，所以笔者选择1/4车辆三质量模型来分析汽车的行驶平顺性[7-8].

依据人-车-路的相互作用建立主动悬架的1/4车辆三质量模型如图1所示.

图1 三质量车辆模型

图中：m1为非簧载质量，即车轮质量；m2为簧载质量，即车身质量；m3为人体质量；kw为轮胎刚度；ks为悬架刚度；kt为座椅刚度；c1为悬架阻尼；c2为座椅阻尼；z1为车轮垂直位移；z2为悬架垂直位移；z3为座椅垂直位移；zg为路面不平度激励；u为作动器的控制力.

根据牛顿第二运动定律，建立车辆模型的动力学方程：

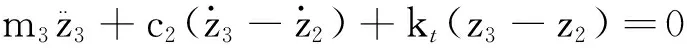
(1)

kt(z3-z2)-u=0.

(2)

ks(z2-z1)=0.

(3)

当上述方程中的u=0时，即将图1中作动器u去掉，该主动悬架车辆模型就变成被动悬架车辆模型.

1.2 主动悬架线性最优控制(LQR)

笔者选择线性最优控制，即LQR作为主动悬架的控制方法.线性最优控制是指在理想系统模型的基础上，采用控制对象的状态响应和控制输入的加权二次型作为性能指标，保证在动态稳定的条件下控制对象实现最优控制[9].

(1) LQR控制状态方程

设系统的状态变量为：

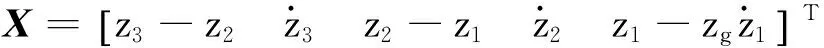
(4)

(5)

式中：

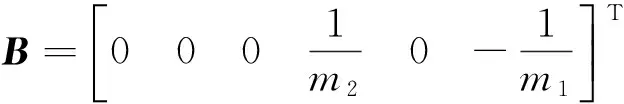
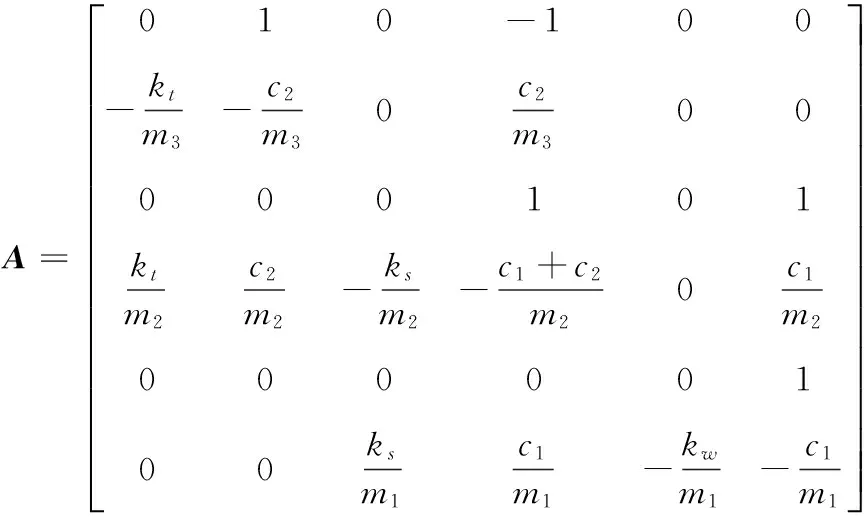
(2) 最优控制器设计

(6)式中：q1、q2、q3为加权系数；r为能量约束系数.将上式写成矩阵形式

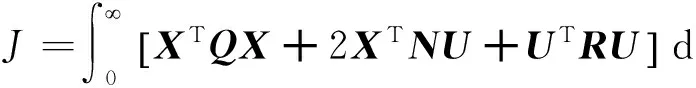
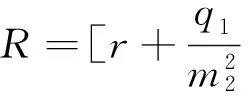
式中：

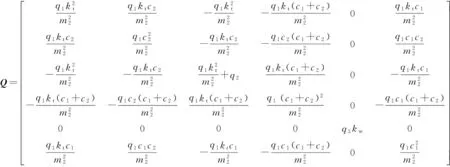
主动悬架的最优控制力为u=-KX.

(8)

其中K=R-1BTP，P可根据如下Riccati微分方程求得[13]

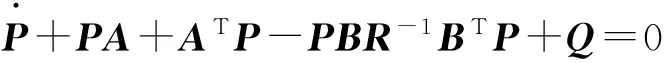
(9)

2 建立随机路面激励模型

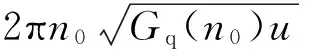
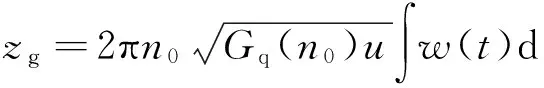
(10)

式中：Gq(n0)为路面不平度系数;u为车速;n0为参考空间频率;w(t)为零均值单位白噪声.

目前我国的路面谱中B、C两级所占比例较大，笔者选取C级路面垂直位移作为激励进行仿真，路面不平度系数Gq(n0)=256×10-6m3，车速v=40 km/h，参考空间频率n0=0.1 m-1，在MATLAB/Simulink中的仿真模型如图2所示，仿真结果如图3所示.

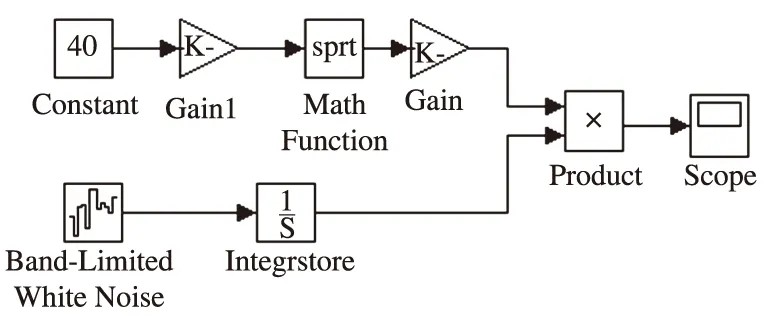
图2 路面谱仿真模型

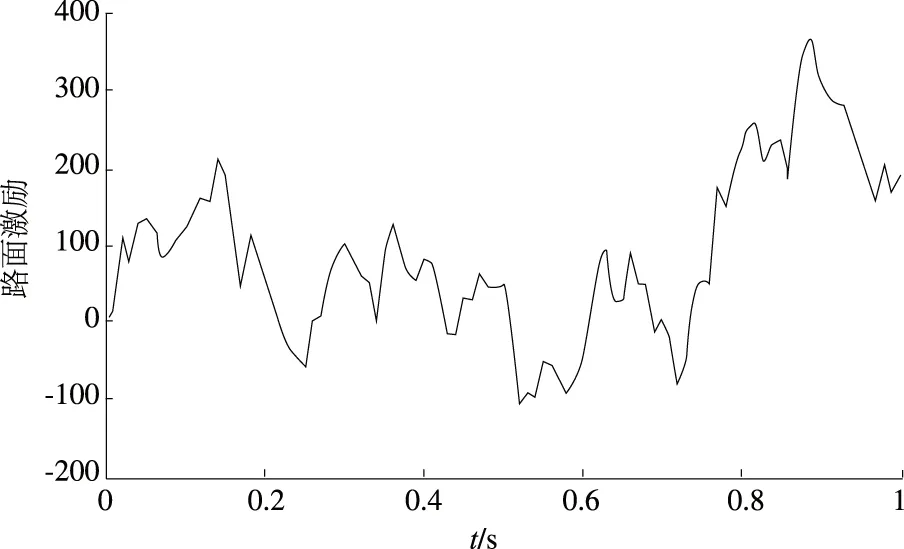
图3 C级路面下白噪声随机路面输入

3 基于Matlab的仿真分析

笔者选用某轿车悬架系统为例，其主要技术参数如表1所示.根据经验积累和反复调试，加权系数和能量约束系数确定为q1=1、q2=5、q3=80 000、r=1.利用MATLAB编程和Simulink仿真模块分别建立主动悬架最优控制的频域仿真模型和时域仿真模型(如图4所示).令作动器的控制力u=0，主动悬架的仿真模型就变为被动悬架的仿真模型.将两种悬架在40 km/h的车速下分别在时域和频域内进行仿真，并将仿真结果进行对比分析.仿真结果如图5～图7所示。

表1 汽车主要质量和性能参数表

图4 基于线性最优控制的主动悬架时域仿真模型

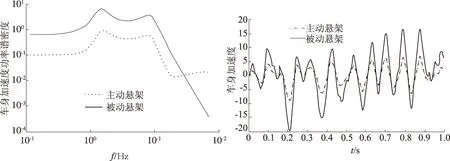
(a)频域仿真曲线 (b)时域仿真曲线

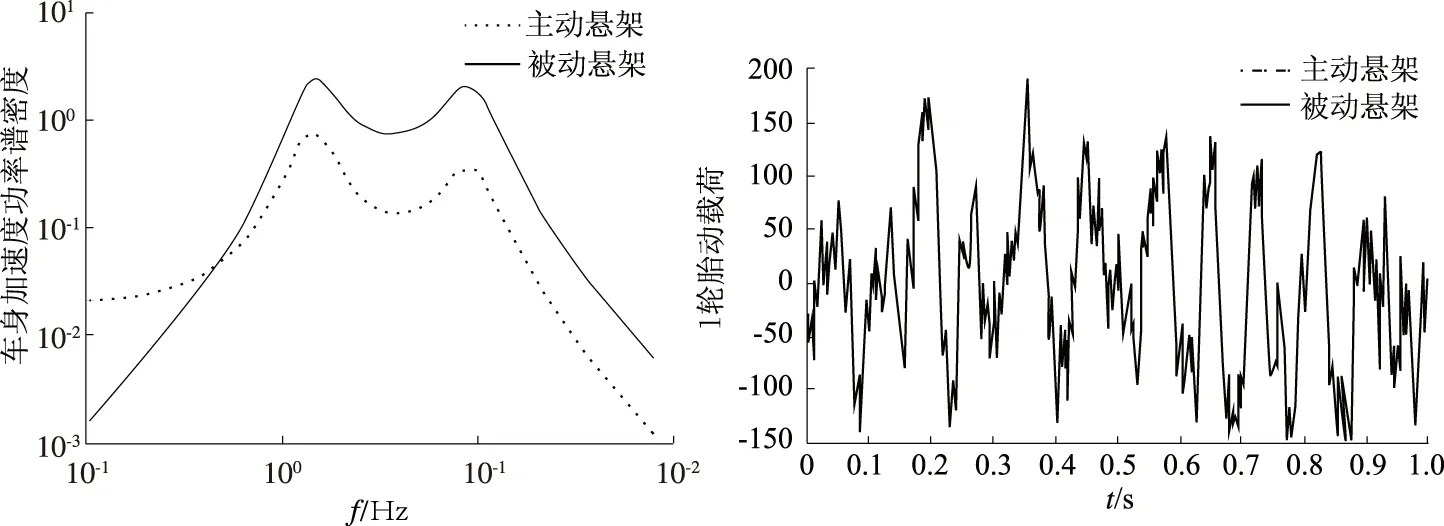
(a)频域仿真曲线 (b)时域仿真曲线

(a)频域仿真曲线 (b)时域仿真曲线

由图5可得：在0.1～50 Hz频段内，主动悬架的车身加速度降为被动悬架的1/8，而在50 Hz以上的频段，主动悬架高于被动悬架，但汽车的工作频率主要集中在中低频段；在时域仿真图中，主动悬架的仿真曲线变化范围在-8～6，而被动悬架的变化范围在-20～17，降幅在60%以上.

由图6可得：在频域仿真图中，在0.1～0.5 Hz频段内，主动悬架的轮胎动载荷高于被动悬架，而在0.5 Hz以上的频段，主动悬架显著降低，降低为被动悬架的1/5；在时域仿真图中，主动悬架和被动悬架的仿真曲线基本重合，没有明显变化.

由图7可得：在频域仿真图中，主动悬架的悬架动挠度比被动悬架有稍微的降低，降幅约为10%左右；而在时域仿真图中，主动悬架悬架动挠度仿真曲线的变化范围在-0.015～0.035，而被动悬架的变化范围在-0.035～0.0.31，降幅在20%以上，从总体上看，主动悬架的曲线更显平顺和收敛.

4 结论

(1)应用线性最优控制的主动悬架能够显著提高汽车的行驶平顺性和操纵稳定性，从而改善了汽车的乘坐舒适性.

(2)相较于被动悬架，主动悬架在车身加速度、轮胎动载荷和悬架动挠度均有明显的改善，其中，在频域范围内，车身加速度降低为被动悬架的1/8，轮胎动载荷降低为1/5，悬架动挠度降低为9/10；在时域内，车身加速度降低了60%，轮胎动载荷没有变化，悬架动挠度降低了20%，表明线性最优控制在改善悬架性能方面起到良好的作用.

(3)基于MATLAB的主动悬架平顺性仿真分析为进一步研究、开发主动悬架积累了宝贵经验，其仿真结果也为汽车悬架的实际设计提供了有益参考.

[1] CHEN S A,LI.X,ZHAO L J，et al.Development of a control method for an eletromagnetic semi-active suspension reclaiming energy with varying charge voltage in steps[J].International Journal of Automotive Technology,2015(5):765-773.

[2] WANG R,JING H,KARIMI H R，et al. Robudt faul-tolerant H∞control of active suspension systems with finite-frequency constraint[J], Mechanical Systemsand Signal Processing ,2015(62):341-355.

[3] JIN Y F,LUO X. Stochastic optimal active control of a half-car Nonlinear suspension under random road excitation[J]. Nonlinear Dyn, 2013(72):185-195.

[4] 桑楠,魏民祥,白玉.基于随机线性最优控制的汽车主动悬架控制器设计[J].郑州大学学报(工学版),2012,33(3):56-60.

[5] MACIEJEWSKI I, GLOWINSKI S,KRZYZYNSKI T.Active control of a seat suspension with the system adaptation to varying load mass[J].Mechatronics.2014,24:1242-1253.

[6] 舒红宇,李伟,何渝生.汽车主动悬架的理论分析及模型试验[J].汽车工程,1999,13(3):129-135.

[7] 陶向华，黄晓明.人-车-路相互作用三质量车辆模型分析[J].交通运输工程学报，2004,4(3):11-15.

[8] 朱强,张越，陈江义,等.混合动力客车独立前悬架运动学建模与操稳性仿真研究[J].郑州大学学报(工学版),2015,36(4):112-115.

[9] 韩文涛,李磊,朱彤.基于线性最优控制理论的汽车主动悬架控制方法研究[J].机械科学与技术,2003(22):55-59.

[10]胡景煌.汽车主动悬架的最优控制分析[J].机电技术,2012,32(1):40-45.

[10]张立军，张天侠.车辆非平稳行驶状态下的半主动悬架 控制[J].振动与冲击,2010,29(6):189-193.

[12]刘艳红,齐书康.基于逆系统方法的永磁同步风力发电系统随机最优控制[J].郑州大学学报(工学版),2015,36(3)16-19.

[13]LI H, TANG C Y,ZHANG T X.Controller of vehicle active suspension systems using LQG method[J].Automation and Logistics.2008,13:401-404.

[14]余志生.汽车理论[M].北京：机械工业出版社,2012.

Research of Simulation in the Linear Optimal Control Active Suspension of Vehicle Based on Matlab

LIU Benxue,LIN Chaoyun,GUO Peidong,LI Liangyu

(College of Mechanical Engineering, Zhengzhou University,Zhengzhou 450001,China)

In order to demostrate that the active suspension is superior in improving the vehicle riding comfort,1/4 vehicle active suspension model and random road excitation model are established.Based on this models,by adopting linear optimal control as the active suspension control strategy, the linear optimal controller is designed.The frequency domain and time domain simulation model of active suspension is established by MATLAB. Frequency domain and time domain simulation of active suspension are carried out respectively under random road excitation and compared with the passive suspension. The results show that the active suspension can effectively reduce the vehicle body acceleration,the dynamic load of the tire and the dynamic deflection of the suspension,thereby improving the ride comfort the handling stability of the vehicle.The model establishement, the optimal design and the simulation analysis of the design provide a useful reference for further research and practical application for active suspension.

vehicle; active suspension; linear optimal control; ride comfort

2016-05-30；

2016-06-19

国家青年科学基金资助项目(11402234)

刘本学(1977—)，男，河南新蔡人，郑州大学讲师，工学博士，主要从事车辆动态仿真与可靠性评估研究，E-mail:liubenxue@zzu.edu.cn.

1671-6833(2016)05-0072-05

U461.4

A

10.13705/j.issn.1671-6833.2016.05.014