对数变换在高分辨距离像目标识别中的应用
孙晶明,杨予昊,邢远见,王梓谦
(1. 中国电子科技集团公司 智能感知技术重点实验室, 南京 210039)(2. 南京电子技术研究所, 南京 210039)
·信号处理·
对数变换在高分辨距离像目标识别中的应用
孙晶明1,2,杨予昊1,2,邢远见1,2,王梓谦1,2
(1. 中国电子科技集团公司 智能感知技术重点实验室, 南京 210039)(2. 南京电子技术研究所, 南京 210039)
在基于高分辨距离像的雷达目标识别中,幂变换是一种常用的非线性预处理方法,对提高识别率有一定的作用。但幂变换对高分辨距离像目标识别的性能提升受信噪比情况影响较大,且幂变换指数的选取对识别结果影响明显,甚至有不利影响。文中针对幂变换存在的问题,提出用对数变换对高分辨距离像进行预处理。比较分析了对数变换与幂变换的作用机理的异同点,并重点分析了对数变换对高分辨距离像类内和类间相关系数的影响。研究表明:对数变换相较于幂变换更适于对高分辨距离像进行预处理,且实测数据的实验结果表明对数变换比幂变换能更有效地提高识别率。
高分辨距离像;目标识别;预处理;对数变换
0 引 言
随着现代军事电子技术的发展,仅能提供目标位置信息的常规雷达已逐渐不能满足现代战争的需要,人们希望了解关于目标进一步详细的信息,对目标识别提出了更高的要求。高分辨距离像(HRRP),即一维距离像,反映了目标的精细结构特征,所以可以直接利用它作为特征向量进行目标识别。同基于合成孔径雷达、逆合成孔径雷达二维像的目标识别技术相比较,HRRP避开了二维像中复杂的运动补偿问题,且易于获得和处理,对目标的运动状态无特殊要求。因此,成为国内外备受关注的研究热点[1-5]。
在基于HRRP的雷达目标识别中,幂变换是一种常用的非线性预处理方法,对提高识别率有一定的作用[6-10]。文献[9]认为利用幂变换进行预处理的理论依据是服从任意概率分布的随机变量经幂变换后更接近于高斯分布,因而可以采用经典的基于高斯分布的分类器来进行识别。在模式识别中,业已证明任何分布通过合适的幂变换都可以将其转化成类正态分布[6,11]。但文献[12]从目标的物理散射机理出发,认为幂变换的渐进高斯性为选用分类器提供了方便,并不是提高识别率的根本原因,而真正的原因在于通过幂变换可以提高雷达目标弱散射点的作用,减少强散射点对弱散射点的屏蔽作用,从而增加了目标之间的可分性。文献[12-13]都对幂变换对HRRP目标识别的性能影响进行了相关研究,认为要根据HRRP的平均信噪比情况来决定是否要用幂变换的方法进行预处理,如果要用幂变换,也应根据具体情况选择合适的幂变换指数,否则对识别有不利影响。
针对幂变换存在的上述问题,本文提出用对数变换对HRRP进行预处理。比较分析了对数变换与幂变换的作用机理的异同点,重点分析了对数变换对HRRP类内和类间相关系数的影响。研究表明对数变换相较于幂变换增大了HRRP类内和类间相关系数的差别,更适于对HRRP进行预处理,且不存在对数变换底数的参数选择问题。通过多种飞机的实测数据,利用滑动相关匹配分类器进行了识别实验,实验结果表明,对数变换比幂变换能更有效地提高识别率。
1 对数变换作用机理分析
先简要介绍对数变换与幂变换的定义,然后从数学原理上对二者进行比较。
设x为原始数据向量,y为转换后的数据向量,则幂变换的转换公式为
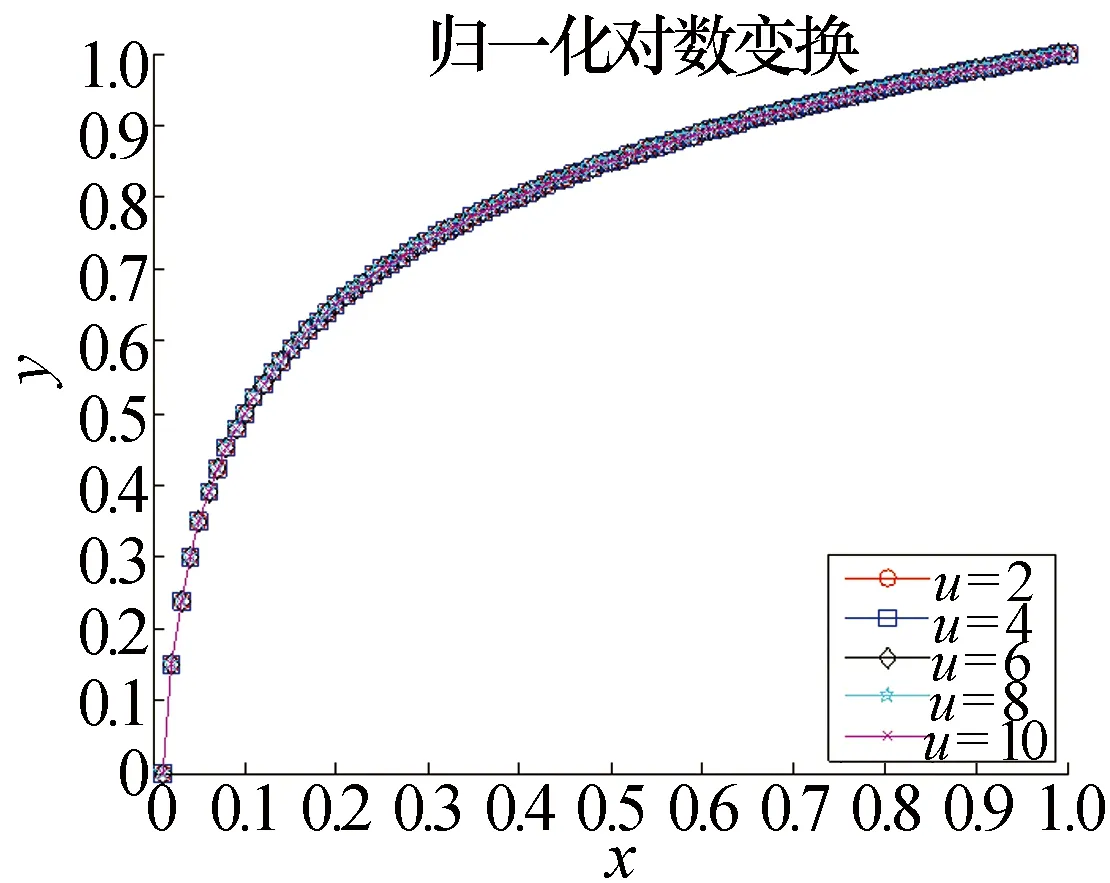
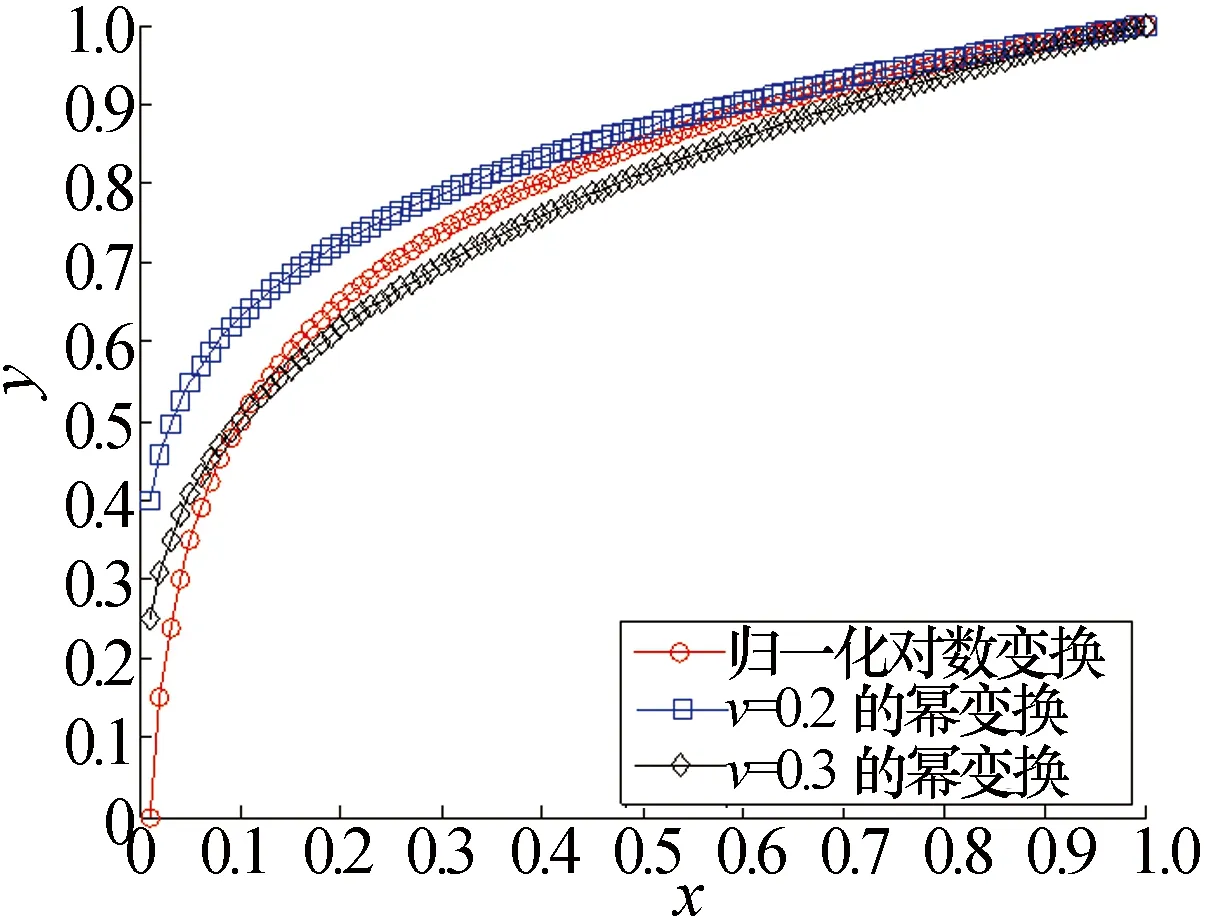
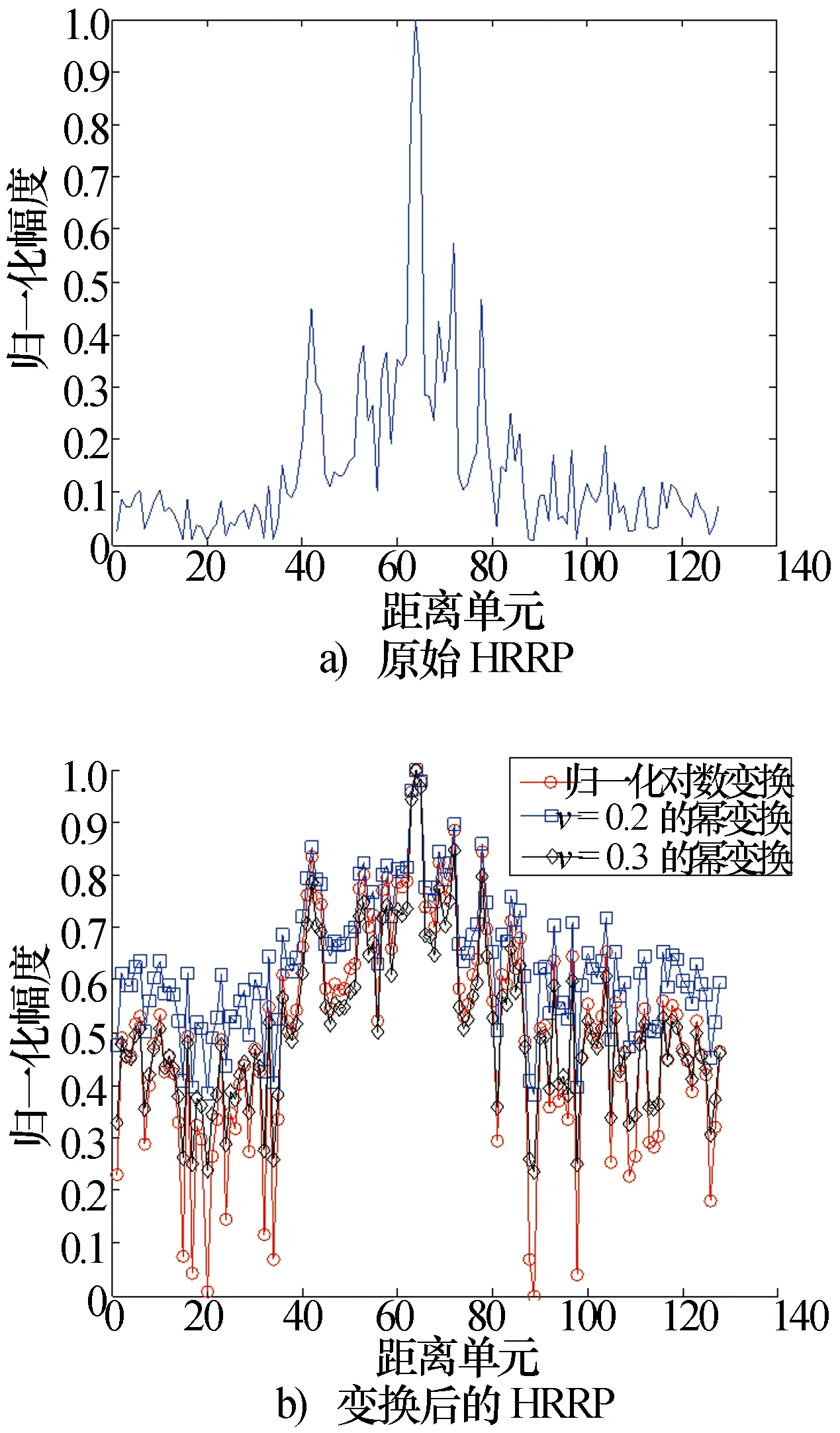
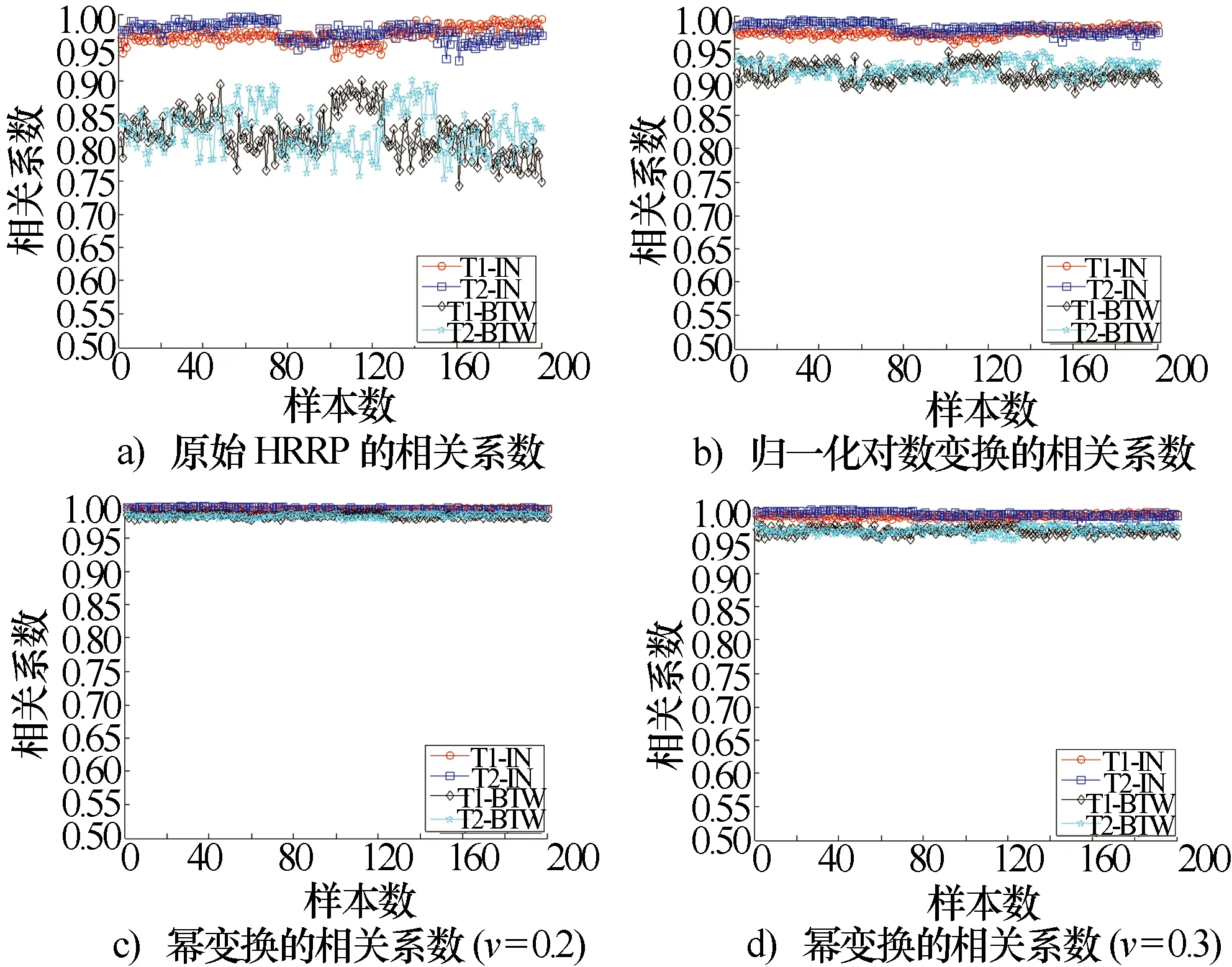
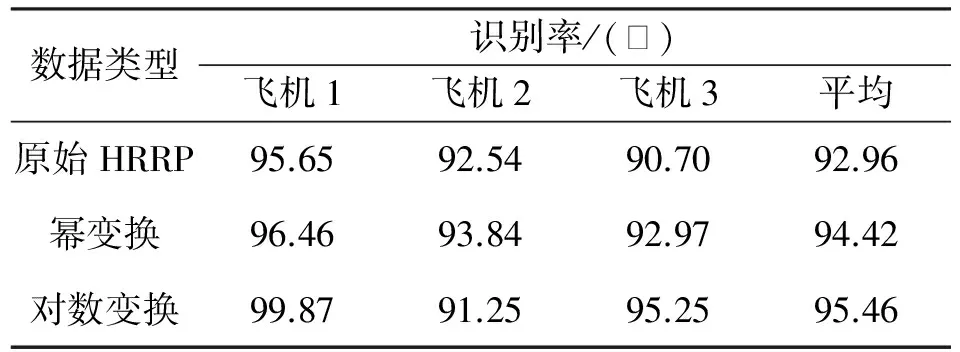
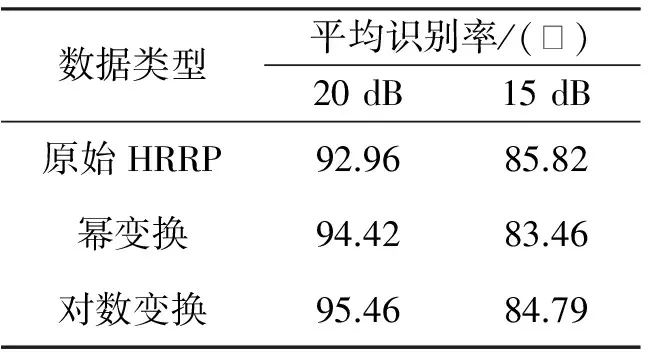
y=xv,0 (1) 式中:v为幂变换指数。当0 对数变换的转换公式为 y=logux,u>1 (2) 式中:u为对数变换底数。这里为何要限定u>1,其原因可通过图1加以说明。 图1 对数变换与幂变换的曲线趋势比较 由于这两种变换都用于对HRRP的预处理,而一般在变换之前都会对HRRP先进行幅度归一化处理。因此,这里限定0 (3) 式中:min(·)表示取最小值;max(·)表示取最大值。我们将其命名为“归一化对数变换”,其曲线趋势如图2所示。 图2 归一化对数变换的曲线趋势 从图2可以看出,归一化对数变换后的数据动态范围与幂变换相同,且曲线趋势与对数变换底数无关,对于这一点给出以下简单的数学推导加以说明。 由于logux对于任意的对数底数u>1都具有相同的函数增减性,其所有极值点的取值位置均相同,所以可设 min(logux)=logux1 (4) max(logux-min(logux))=logux2-logux1 (5) 联立式(3)、式(4)、式(5)可得 孔狄亚克认为知识起源于经验,发端于感觉;没有经验和感觉就不可能有知识。马克思主义认为,物质决定意识,而知识其实是人在认识事物的过程中总结出的规律性的东西。关于知识从哪里来,我们不去进行艰涩的哲学讨论,但知识的产生一定基于某种动力源,并同时呼应知识生产的内在逻辑。 (6) 式中:x1,x2∈x;a为某一确定的对数底数。显然,由式(6)可知,y的变化趋势与对数变换底数u无关,即证明了图2所示的结果。 下面比较一下归一化对数变换与幂变换的曲线趋势,如图3所示,以揭示其物理意义。 图3 归一化对数变换与幂变换的曲线趋势比较 从图3可以看出,在保持较大值的贡献的前提下,幂变换对较小值的贡献提升作用整体强于归一化对数变换。换言之,对HRRP进行预处理时,幂变换在强化弱散射点作用的同时,不自觉地强化了噪声和干扰的作用,而归一化对数变换则较好地平衡了弱散射点与噪声和干扰之间的强化性能。由于其他指数的幂变换在强化噪声、干扰与本体信号之间的平衡性更差,这里不作比较。因此,从作用机理上看,归一化对数变换对HRRP的有利影响应大于幂变换,且归一化对数变换不存在对数变换底数的参数选择问题。 分别用幂变换和归一化对数变换的方法对HRRP进行预处理,比较其预处理前后的差异,如图4所示。 图4 变换后的HRRP与原始HRRP比较 从图4可以看出,幂变换对幅度小的距离单元进行了放大,弱散射点的作用被加强,减弱了强散射点存在时对弱散射点的屏蔽作用,增加了目标之间的可分性,有利于识别;但是,当信号的信噪比较低时,噪声在HRRP中占相当大的比重,经幂变换后噪声的作用被大大加强,使得某些有用信号几乎被噪声“淹没”,此时的HRRP与原始HRRP相比形状大大改变,而且幂指数越小,幂变换对幅度小的距离单元的放大作用越明显。而归一化对数变换的作用虽然与幂变换类似,但对一些极小值点的放大却弱于幂变换,这在一定程度上抑制了噪声的加强,更有利于识别。 HRRP经过变换处理之后,其幅度起伏特性发生了变化。而识别性能不仅与特征向量有关,还与所用的分类器有关。滑动相关匹配分类器是基于HRRP的雷达目标识别常用方法之一,其原理就是将测试样本分类为与其“最相近”的模板所属类别,采用最大相关系数指标以衡量测试样本与模板“相近”的程度。相关系数是衡量特征可分性的一个度量,对于两类样本,如果相关系数大,说明二者具有很大的相似性,不利于分类;反之,如果二者之间的相关系数小,则说明二者差别很大,有利于分类。下面从相关系数的角度研究归一化对数变换对HRRP的影响,并与幂变换进行比较。 对于两类样本,设xi∈Ck(i=1,2,…,Nk,k∈{1,2}),xi为样本数据向量,Ck表示类别,Nk为类别k的样本总数。类内相关系数定义为 corIN(xi)=max(corr(xi,yj)) (7) 式中:corr(·)表示取相关系数;yj∈Ck(j=1,2,…,Nk,j≠i)。 类间相关系数定义为 corBTW(xi)=max(corr(xi,yj)) (8) 式中:yj∈Cq(j=1,2,…,Nq,q∈{1,2},q≠k)。 根据式(7)和式(8),得到变换前后的HRRP类内和类间相关系数变化情况,如图5所示。从图5可以看出,原始HRRP的类内和类间相关系数差别较大,类内相关系数都在0.9以上,而类间相关系数都在0.9以下,两类目标的样本可分性较好,而变换都提高了类内相似性。比较图5b)、图5c)和图5d)可知,经过变换之后,类内和类间相关系数差别减小;但与幂变换相比,归一化对数变换后的相关系数差别相对较大。因此,从相关系数的角度,我们可以得出结论:归一化对数变换相较于幂变换更适于对HRRP进行预处理。 图5 变换前后的HRRP类内和类间相关系数变换比较 从相关系数的角度,变换会减弱各目标类别之间的区分性,但识别率还与识别算法、分类器性能等因素有关。那么,归一化对数变换能否提高HRRP目标识别率呢?本文将通过实测数据的实验结果进行验证。 实验采用的实测数据为某S波段精密跟踪雷达所采集到的数据,雷达带宽为200 MHz,目标是三种飞机。一般的HRRP目标识别流程如图6所示。 图6 识别流程图 预处理包括:主峰对齐、目标支撑域长度提取、去除噪声基底、对数变换(或幂变换)、能量归一化。主峰对齐主要是为了减小HRRP平移敏感性的影响;目标支撑域长度提取一方面是为了统一HRRP的数据处理长度,另一方面是为了减小噪声影响;去除噪声基底是为了提高信噪比,即设置噪声门限(门限可取噪声平均幅值的若干倍),将低于门限值的幅度值置为零;对数变换(或幂变换)是为了提高弱散射点在识别中的作用,同时减弱强散射点存在时对弱散射点的屏蔽作用,从而增加目标之间的可分性;能量归一化主要是为了减小HRRP幅度敏感性的影响。 这里的特征提取与矩阵变换实际上并未起作用,因为用的是预处理后的HRRP进行相关匹配。测试时,采用±8°小角域滑动相关匹配分类器进行识别,主要是为了减小HRRP姿态敏感性的影响。 实验1取这三种目标在多种不同姿态角下的HRRP进行处理,信噪比为20 dB,对应以上三种飞机分别取了1 500个HRRP进行测试,结果如表1所示。 表1 变换前后的HRRP识别率比较 从表1可以看出,在信噪比较高时,对数变换和幂变换均能提高识别率,是因为变换后目标特征将更加明显,特别是幅度较小的弱散射点目标信息被放大加强,减弱了强散射点存在时对弱散射点的屏蔽作用。与幂变换相比,对数变换的识别率更高。 实验2将分析识别率与信噪比之间的关系。所用数据与实验1相同,采用加高斯白噪声的方法,使平均信噪比达到15 dB,然后再做预处理和分类识别,结果如表2所示。 表2 不同信噪比下的HRRP识别率比较 从表2可以看出,当信噪比降低时,变换前后的HRRP识别率均下降明显,变换适用的信噪比范围应在20 dB以上。变换后的HRRP识别率低于原始HRRP的识别率,是因为相比于有用信号,变换对噪声的放大尤为明显,变换后目标就被“淹没”在噪声中了,此时变换并不能改善识别率,甚至会降低识别率。与幂变换相比,对数变换对噪声的放大作用弱一些,因而对数变换的识别率更高。 综合以上分析,若直接使用HRRP作为特征向量进行目标识别,与幂变换相比,对数变换更适于对HRRP进行预处理,其识别率更高。但在低信噪比时,变换后的识别性能要低于原始HRRP,但对数变换的识别率仍高于幂变换。因此,在用HRRP对目标进行识别时,要根据HRRP的平均信噪比情况来决定是否要用对数变换的方法进行预处理。当然,若选择更好的识别算法和分类器,对数变换对HRRP识别性能的影响还有待进一步研究。 [1] SHAW A K. Automatic target recognition using high-range resolution data[R]. ADA343438. Fairborn, Ohio: Wright State University, 1998.[2] HE S H, ZHANG W, GUO G R. Target discrimination and recognition using high resolution range features[C]// Proceedings of IEEE National Aerospace and Electronics Conference. [S.l.]: IEEE Press, 1992: 280-283. [3] ZYWECK A, BOGNER R E. Radar target classification of commercial aircraft[J]. IEEE Transactions on Aerospace and Electronic Systems, 1996, 32(2): 598-606. [4] LI H J, YANG S H. Using range profile as feature vectors to identify aerospace objects[J]. IEEE Transactions on Antennas and Propagation, 1993, 41(3): 261-268. [5] WILLIAMS R, WESTERKAMP J, GROSS D, et al. Automatic target recognition of time critical moving targets using 1D high range resolution (HRR) radar[J]. IEEE Aerospace and Electronic Systems Magazine, 2000, 15(4): 37-43. [6] FUKUNAGA K. Introduction to statistical pattern recognition[M]. San Diego: Academic Press, 1990. [7] BHATNAGAR V, SHAW A K, WILLIAMS R W. Improved automatic target recognition using singular value decomposition[C]// Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing. [S.l.]: IEEE Press, 1998(5): 2717-2720. [8] SHAW A K, BHATNAGAR V. Automatic target recognition using eigen-templates[C]// SPIE Conference on Algorithms for Synthetic Aperture Radar Imagery V. Orlando: SPIE Press, 1998: 448-459. [9] 高 倩, 刘家学, 吴仁彪. 基于平均模板的HRRP自动目标识别[J]. 现代雷达, 2003, 25(3): 14-17. GAO Qian, LIU Jiaxue, WU Renbiao. Automatic target recognition based on HRRP mean-templates[J]. Modern Radar, 2003, 25(3): 14-17. [10] 陈艺慧, 郑高峰, 孙道恒. 声表面波射频识别技术及其发展[J]. 电子机械工程, 2012, 28(3): 1-6. CHEN Yihui, ZHENG Gaofeng, SUN Daoheng. Surface acoustic wave radio frequency identification technology and its development[J]. Electro-Mechanical Engineering, 2012, 28(3): 1-6. [11] 辛 宁, 张 静, 王国宏, 等. 雷达目标识别中幂变换的正态性研究[J]. 现代雷达, 2007, 29(7): 48-51. XIN Ning, ZHANG Jing, WANG Guohong, et al. Research on normality of power transform in radar target recognition[J]. Modern Radar, 2007, 29(7): 48-51. [12] 徐海丽, 王 洋. 幂变换在一维距离像目标识别中的作用分析[J]. 现代雷达, 2011, 33(9): 37-41. XU Haili, WANG Yang. Performance of power transform in high resolution range profiles target identification[J]. Modern Radar, 2011, 33(9): 37-41. [13] 王俊鸣, 李 华, 张子华, 等. 幂变换对雷达目标HRRP识别的性能影响[J]. 现代雷达, 2010, 32(9): 55-58. WANG Junming, LI Hua, ZHANG Zihua, et al. Performance effect of power transform on HRRP identification based on radar target[J]. Modern Radar, 2010, 32(9): 55-58. 孙晶明 男,1984年生,博士,工程师。研究方向为压缩感知、雷达成像与目标识别、雷达信号处理。 Application of Logarithm Transform in High Resolution Range Profile Target Recognition SUN Jingming1,2,YANG Yuhao1,2,XING Yuanjian1,2,WANG Ziqian1,2 (1. Key Laboratory of InteliSense Technology, CETC, Nanjing 210039, China)(2. Nanjing Research Institute of Electronics Technology, Nanjing 210039, China) In radar target recognition based on high resolution range profile, power transform is a common nonlinear preprocessing method, which can improve the recognition rate. But the performance of high resolution range profile target recognition with power transform is seriously affected by signal-to-noise ratio, and the recognition result is significantly affected by the choice of the power transform exponential, even the effect is adverse. In this paper, logarithm transform is raised for high resolution range profile preprocessing to solve the problems of power transform, and a comparative analysis of the similarities and differences between the mechanism of logarithm transform and power transform is provided, and the impact of logarithm transform on the intra-class and inter-class correlation coefficients of high resolution range profiles is analyzed. The results show that logarithm transform is more suitable for high resolution range profile preprocessing than power transform, and the experimental results based on measured data show that logarithm transform can more effectively improve the recognition rate than power transform. high resolution range profile; target recognition; preprocessing; logarithm transform 10.16592/ j.cnki.1004-7859.2016.11.009 孙晶明 Email:sjm@hust.edu.cn 2016-08-29 2016-10-19 TN911.7 A 1004-7859(2016)11-0040-04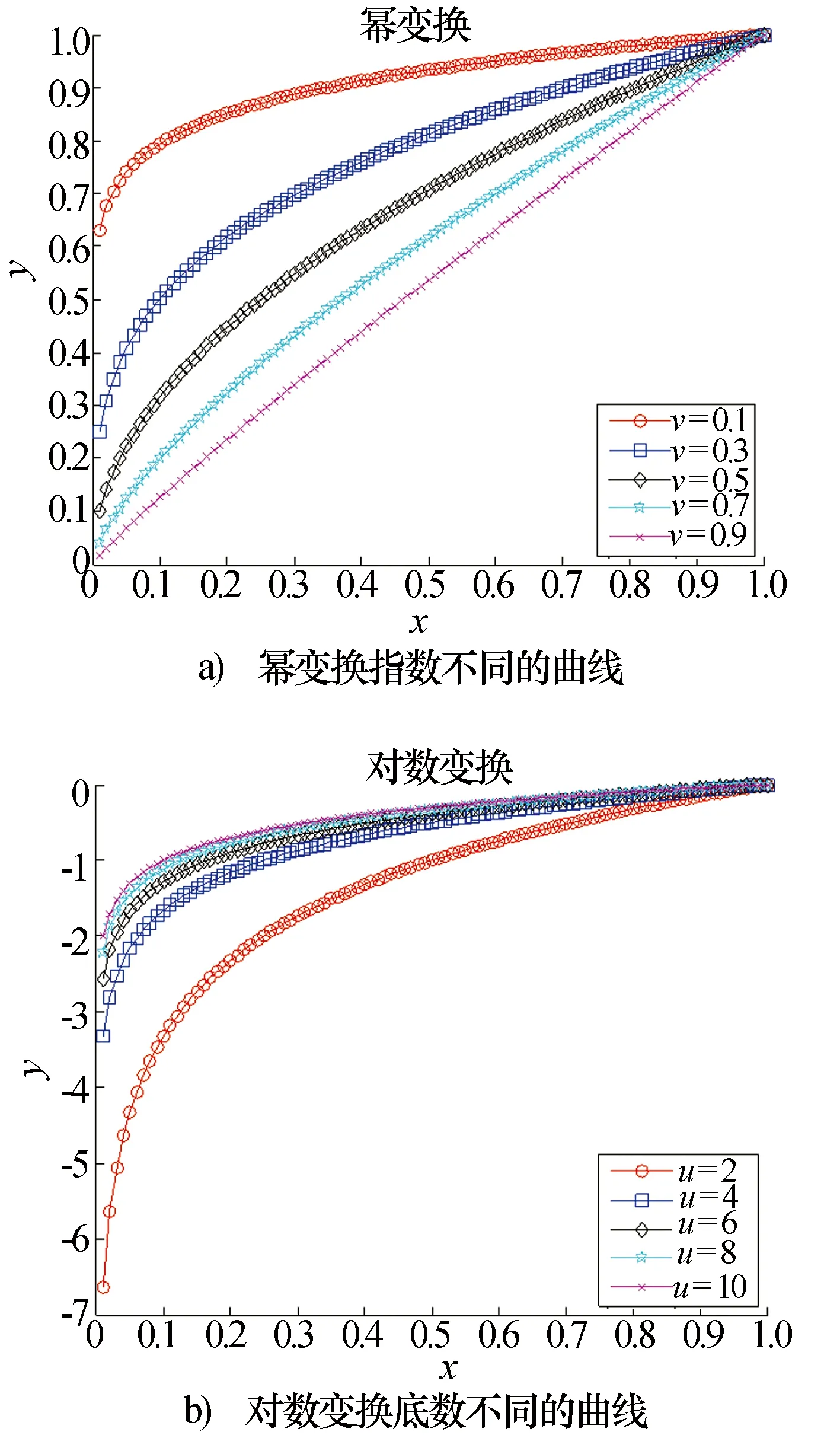
2 对数变换对HRRP的影响
3 实验结果及分析

4 结束语

