改进的雷达信号识别效能评估方法

张 强，王红卫，陈 游

(空军工程大学 航空航天工程学院, 西安 710038)



·总体工程·

改进的雷达信号识别效能评估方法

张 强，王红卫，陈 游

(空军工程大学 航空航天工程学院, 西安 710038)

针对以往雷达信号识别效能评估方法中评估指标选取模糊、指标权重设置单一、评估排序不合理的问题，提出了基于IAHP-Entropy-I2TOPSIS模型改进的雷达信号识别效能评估方法。其主要思路是基于识别率测试结果建立树状评估指标体系；采用IAHP和Entropy分别确定主观指标权重和客观指标权重，并通过线性组合方法确定综合权重；运用区间型多属性决策的夹角度量法改进区间TOPSIS得到I2TOPSIS并依此进行评估排序。最后通过实例仿真，验证了所提方法的有效性。

雷达信号；效能评估；评估指标；区间；综合权重

0 引 言

雷达信号识别是电子情报侦察、电子支援侦察和雷达威胁告警系统中的关键处理过程，也是对敌遂行电子干扰的前提和基础，其识别水平是衡量雷达对抗设备技术先进程度的重要标准[1]。随着雷达信号识别技术的日益发展和在军事领域尤其是在电子对抗中的广泛应用，全面准确地对识别效能进行有效评估显得更加重要[2]。

原有的雷达信号识别效能评估方法都是基于识别准确率这个评估指标，随着战场电磁环境日趋复杂，这类评估方法难以达到合理和全面的要求。针对这个问题，在建立了较好的评估指标体系的前提下，文献[3]提出了基于层次分析法(AHP)的评估方法，文献[4]提出了基于AHP和逼近理想解排序法(TOPSIS)综合评判的评估方法，文献[5]提出了基于区间TOPSIS的评估方法等。这些评估方法能够较好地对识别效能进行评估，但也存在着明显的问题。首先，在评估指标方面，普遍存在选取准则模糊和选取指标单一的问题；其次，在评估指标权重设置方面，文献[3]和文献[4]采用AHP设置权重，只考虑了主观因素，文献[5]中采用熵权法(Entropy)设置权重，只考虑了客观因素，都存在着仅仅考虑单一方面因素的问题；最后，在评估排序方面，文献[4]中采用传统TOPSIS法，存在距离正理想解近的方案同时也距离负理想解近的问题，文献[5]中采用区间TOPSIS法(ITOPSIS)，虽然利用区间距离计算贴近度更加合理，但存在和文献[4]同样的问题。

对以往雷达信号识别效能评估中存在的上述问题，并考虑到战场电磁环境的复杂性和不确定性，本文基于识别测试结果(MRR)[6-8]建立了评估指标体系，提出了基于IAHP-Entropy-I2TOPSIS模型改进的雷达信号识别效能评估方法，主要思路是：考虑主观因素，采用区间AHP(IAHP)求得主观指标权重，考虑客观因素，采用熵权法(Entropy)求得客观指标权重，再通过线性组合方法求出综合指标权重，以解决评估指标权重设置不合理的问题；采用区间型多属性决策的夹角度量法改进ITOPSIS得到I2TOPSIS(Improved Interval TOPSIS, I2TOPSIS)并依此进行评估排序，以解决TOPSIS评估排序不合理的问题。最后通过仿真，验证了所提方法能解决原有方法存在的问题，可以合理准确地对雷达信号识别效能进行评估。

1 评估指标的建立

评估指标体系是雷达信号识别效能评估模型的重要组成部分，科学地选取评估指标是正确进行评估的前提。原有对雷达信号识别效能的评估都是基于识别准确率这个单一指标，首先，采用单一指标进行评估无疑是不科学和不系统的。再者，通过识别准确率进行评估存在以下局限：(1)不能确定识别系统的识别率真值所需的原始测试数量；(2)不能确定所得识别率的置信区间；(3)不能将识别率等效为识别方法的能力；(4)不能有效评价识别结果的稳定性问题[7]。针对上述识别准确率存在的弊端，本文采用识别率测试结果(MRR)建立树状评估指标体系。MRR是指将n次测试结果均分成m组，分别求取每组n/m个测试结果的均值，即可得到m个MRR样本。针对雷达信号识别系统，若有k个雷达信号，则会生成k×m个MRR样本，但由于算法和求解的一致性，研究单个雷达信号的MRR样本即可。由于MRR是一个变量，有分布、均值和方差，以及与外界条件的独立性，因此，利用MRR可以准确地对雷达信号的识别效能进行评估。关于确定MRR样本容量及生成MRR样本在文献[8]中有详细介绍，在此不再赘述。

选取评估指标应该按照一定的选取准则。本文按照科学性准则、系统性准则和目的性准则，根据雷达信号识别结果的特点，选择正确性、稳定性、独立性和识别代价作为效能评估准则，并得到相应的评估指标[8]。具体的雷达信号识别评估指标体系如图1所示。

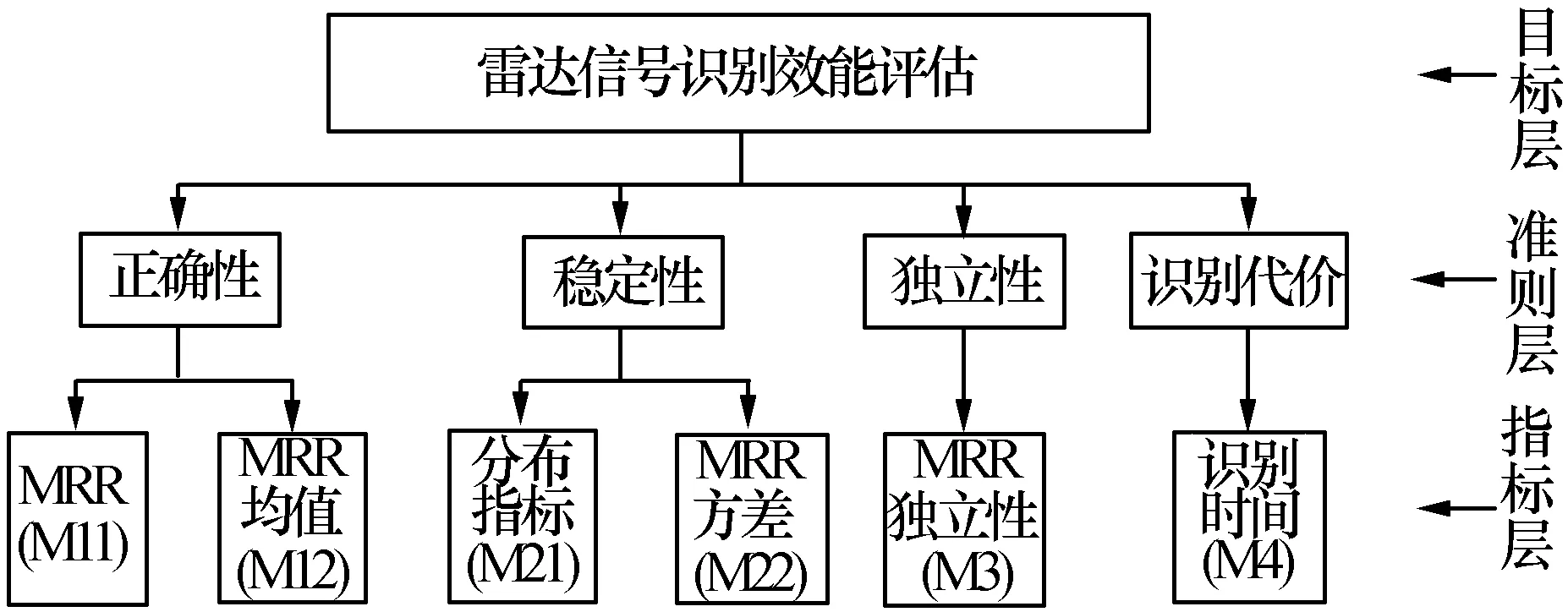
图1 雷达信号识别评估指标体系

2 改进的区间TOPSIS模型

2.1 ITOPSIS法

TOPSIS法是由王先甲[9]等提出的一种适用于根据多属性指标对多个评估对象进行比较选择的分析方法。ITOPSIS法是对指标为区间数的评估对象进行评估的一种TOPSIS方法，需用到区间数运算法则进行计算。ITOPSIS能在信息不完备情况下，对不确定性问题进行评估排序，适用于战场电磁环境。具体计算步骤如下：

步骤1：建立决策矩阵R

(1)

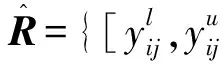
通过权重W={w1,w2,…,wn}，得到加权规范化决策矩阵

(2)

步骤4：确定正理想解S+与负理想解S-

(3)

(4)

式中：J+和J-分别为效益型指标集和成本型指标集。

(5)

(6)

步骤6：计算各评估对象的相对贴近度Ci

(7)

相对贴近度Ci为0～1之间的无量纲数，反映了评估对象靠近正理想解远离负理想解的程度，其值越大，性能越好。

2.2 I2TOPSIS评估模型

ITOPSIS和TOPSIS存在着评估排序不合理的问题，即与正理想解欧式距离更近的评估对象可能与负理想解欧式距离也近，因此，按照欧氏距离计算相对贴近度，不能完全准确地评估相关方案的优劣。区间型多属性决策的夹角度量法放弃采用欧式距离计算相对贴近度，改用各评估对象与正负理想解的夹角定义相对贴近度，依此对ITOPSIS进行改进得到I2TOPSIS，较好地解决了评估排序不合理的问题。且I2TOPSIS具有和ITOPSIS同样的处理不确定性问题的能力。

首先，定义各评估对象与正负理想解的夹角分别为

(8)

(9)

然后，依据各评估对象与正负理想解的夹角重新定义相对贴近度

(10)

Ui同样反映了评估对象靠近正理想解远离负理想解的程度，其值越大，越靠近正理想解，评估对象性能越好。

3 IAHP-Entropy-I2TOPSIS模型的建立

3.1 运用IAHP确定主观指标权重

AHP是由Satty提出的一种实用的多属性决策方法。IAHP是基于常规AHP扩展的多属性决策方法，在AHP法的基础上融入了区间数的特性，能有效对不确定因素进行决策分析，适用于战场电磁环境。采用IAHP法确定主观指标权重步骤如下：

步骤1 构造区间判断矩阵A

评估指标体系确定后，依据互反性1～9标度[10]，按照实际情况与要求做出两两比值判断，列出区间判断矩阵A。

(11)

步骤2 区间判断矩阵的一致性检验

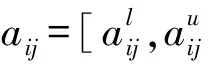
(12)

(13)

若α≤1且β≥1，则区间判断矩阵具有较好的一致性；若α>1或β<1，则区间判断矩阵一致性较差，需进行重新判断，直至取得良好的一致性。

步骤3 求解区间判断矩阵权重Wz。

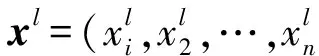
Wz=[αxl, βxu=(w1,w2,…,wi,…,wn)

(14)

使用区间权重进行加权计算，将会拉宽所得矩阵中元素的区间宽度，导致评估结果失准，故采用权重区间上下限的平均值，并对其进行归一化后作为最终的主观指标权重。

3.2 运用Entropy确定客观指标权重

应用熵可以度量评估指标体系中指标数据所蕴涵的信息量，并依此确定各指标的权重。基于Entropy确定客观指标权重的步骤如下：

步骤1：计算各指标的信息熵Ej

(15)

步骤2：计算各指标的熵权值wj

(16)

步骤3：确定客观指标权重Wk

Wk=[W1,W2,…,Wn]

(17)

3.3 确定综合指标权重

为了清楚的研究权重的变化对评估结果带来的影响，本文选择线性组合方法确定综合指标权重，设平衡因子分别为η和μ，则综合指标权重为

W=ηWz+μWk

(18)

η+μ=1

(19)

综合指标权重W不仅考虑了主观的专家知识与工作经验，而且考虑到了客观的数据本身的信息，能够全面的反映评估指标的相对重要程度。

3.4 IAHP-Entropy-I2TOPSIS模型

IAHP-Entropy-I2TOPSIS模型具体的计算步骤如下：

步骤1：建立原始决策矩阵R；

步骤3：运用IAHP确定主观指标权重Wz，运用Entropy确定客观指标权重Wk，通过线性组合确定综合指标权重W；

步骤5：确定正理想解S+与负理想解S-；

步骤6：计算各评估对象与正理想解的夹角θ+与负理想解的夹角θ-；

步骤7：计算各评估对象相对贴近度Ui。

4 仿真分析

针对雷达信号识别实例，本文选取SNR为0 dB条件下8类信号的平均复杂度特征[12]作为实验所用的特征参数，如表1所示。

表1 复杂度特征值

本文选取概率神经网络(PNN)、支持向量机(SVM)、基于遗传算法的支持向量机(GA-SVM)、基于蚁群算法的支持向量机(ACO-SVM)和基于粒子群算法的支持向量机(PSO-SVM)[13]算法，对6种算法识别结果进行效能评估。其中，GA-SVM的代沟为0.9，弹性因子为1；ACO-SVM的挥发因子为0.9，步长为0.1；PSO-SVM的惯性权重为0.9，弹性因子为1，其余识别算法中的参数设置采用默认值。

依据本文3.4节IAHP-Entropy-I2TOPSIS模型的具体计算步骤，先通过平台仿真获得原始决策矩阵，如表2所示；并采用向量规范法对其进行处理，获得规范化决策矩阵，如表3所示。仿真实验的主演思路是：首先，分别使用IAHP和Entropy确定主客观指标权重；然后，运用线性组合确定综合指标权重；最后，利用I2POSIS完成对6种算法的识别效能评估实验。

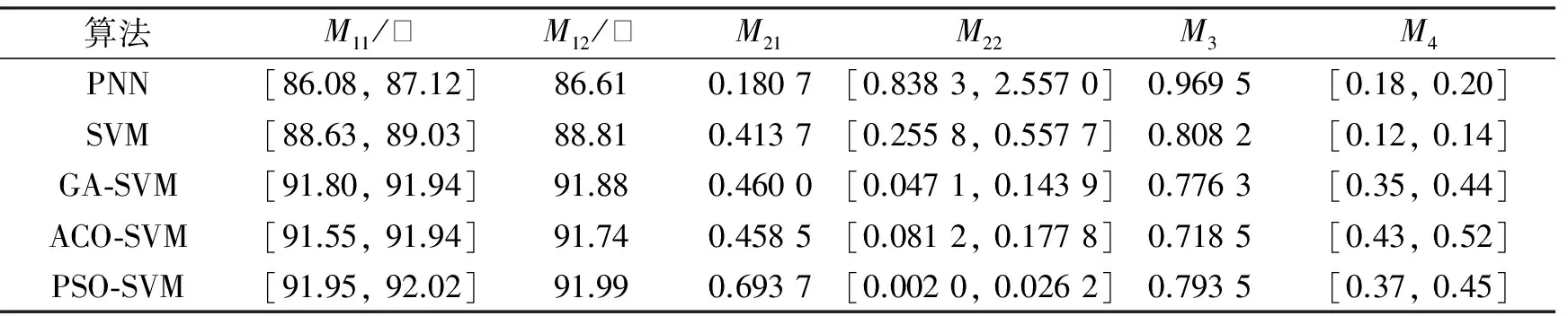
表2 原始决策矩阵

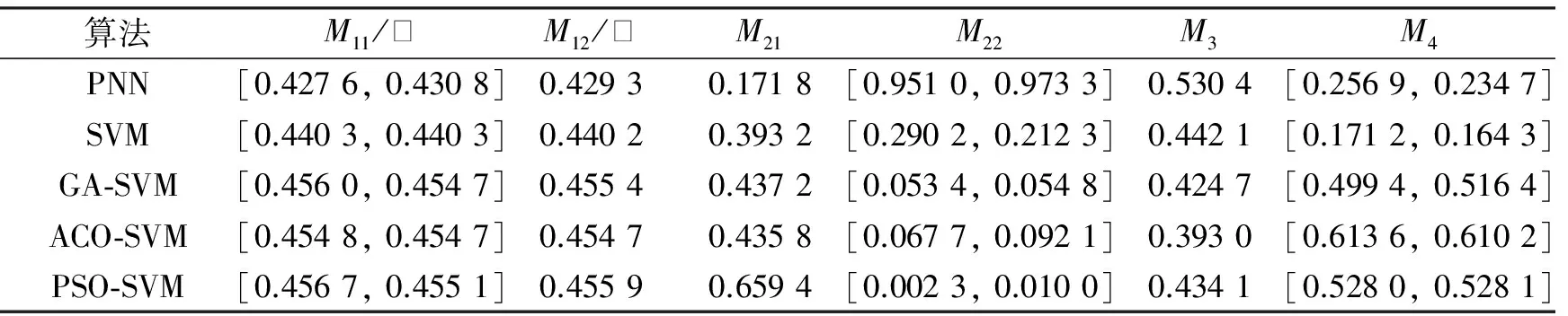
表3 规范化决策矩阵

4.1 主客观及综合指标权重的确定

根据IAHP的基本原理、文献资料和专家经验，构造目标层对应于准则层的区间判断矩阵为

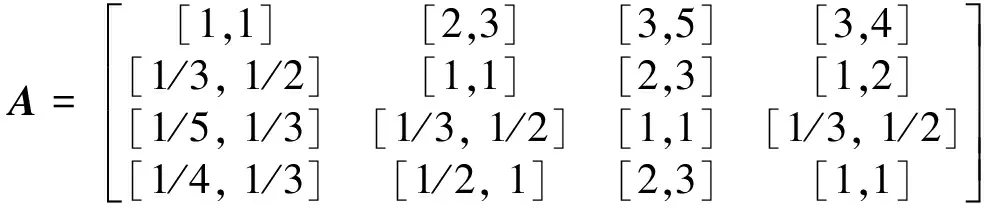
(20)

依据本文3.1节IAHP法确定主观指标权重步骤，首先，根据式(12)和式(13)对区间判断矩阵进行一致性检验，计算可得α=0.940 8，β=1.064 9，可见α≤1且β≥1。因此，构造的准则层区间判断矩阵具有良好的一致性，进一步可求得准则层权重向量为Wz-M=[[0.813 8, 0.902 7],[0.349 2, 0.425 6], [0.152 1, 0.176 3], [0.278 8, 0.327 0]]。

经检验，所有指标层区间判断矩阵满足一致性要求，并采用IAHP获得相应权重。其权重分别为Wz-M1=[[0.361 9, 0.393 4],[0.601 3, 0.755 7]]，Wz-M2= [[0.5, 0.5],[0.5,0.5]]，Wz-M3=[1,1]，Wz-M4=[1,1]。则最终确定的主观指标权重Wz=[0.1840, 0.3318, 0.109 7, 0.109 7, 0.093 0, 0.171 6]。

依据本文3.2节Entropy法确定客观指标权重步骤，对规范化决策矩阵，通过式(15)求得信息熵为E=[0.9010, 0.9021, 0.9796, 0.9855, 0.9222,0.936 3]，通过式(16)和式(17)最终确定的客观指标权重Wk=[0.265 2,0.262 3, 0.054 6, 0.038 8, 0.208 4, 0.170 6]

依据本文3.3节的线性组合方法确定综合指标权重，总共分为5种组合进行研究，分别为η=1、μ=0、η=0.75、μ=0.25、η=0.5, μ=0.5、η=0.25, μ=0.75和η=0，μ=1。不同线性组合下综合指标权重如表4所示。

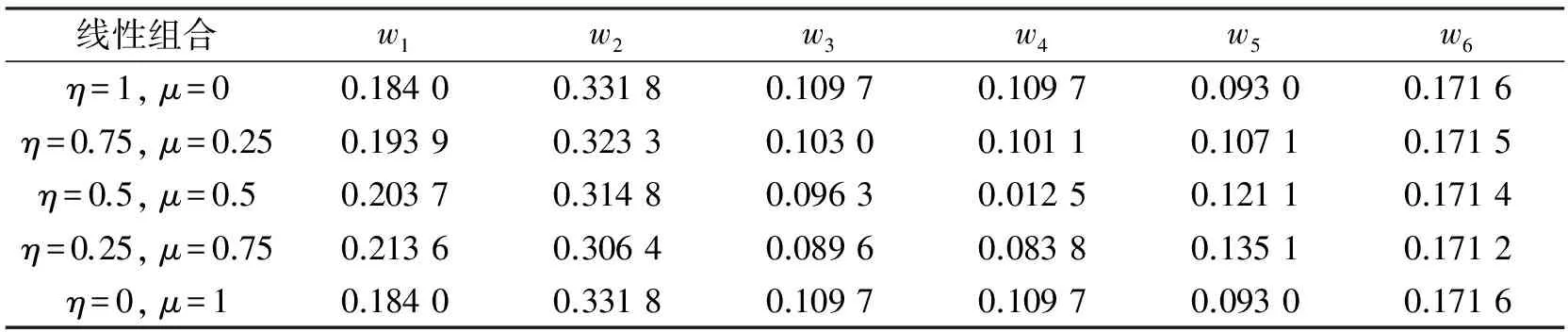
表4 不同线性组合下综合指标权重

4.2 识别效能评估实验

确定了5种线性组合下的综合指标权重后，运用Matlab按照本文3.4节的计算步骤，首先，确定5种综合权重下的正负理想解；然后，确定各评估对象与正负理想解的夹角；最后，确定各评估对象的相对贴近度。

由于篇幅所限，本文只给出不同线性组合下的各评估对象的相对贴近度数据，如表5所示。

表5 不同线性组合下各识别算法相对贴近度

由表5相对贴近度大小可确定各评估对象的优劣排序。当η=1,μ=0时，表示只考虑了主观权重，未考虑客观权重；当η=0.75,μ=0.25时，表示以主观权重为主，客观权重为辅；当η=0.5,μ=0.5时，表示主客观权重同样重要。这3种综合权重下的各识别算法的排序相同，均为UPSO-SVM>UACO-SVM>UGA-SVM>UPNN>USVM；当η=0.25,μ=0.75时，表示以客观权重为主，主观权重为辅，此时UPSO-SVM>UACO-SVM>UGA-SVM>USVM>UPNN；当η=0，μ=1时，表示只考虑了客观权重，未考虑主观权重，此时UPSO-SVM>UGA-SVM>UACO-SVM>USVM>UPNN。

5种综合权重下各识别算法效能评估共有3种排序，将其进行对比，并结合以往的研究共识[13]，可得当η=0.25,μ=0.75时的识别效能评估排序是符合实际情况的，即UPSO-SVM>UACO-SVM>UGA-SVM>USVM>UPNN。

综上可得出如下结论：权重变化会造成识别效能评估排序发生变化，在设置权重上，单一采用主观权重和单一采用客观权重都是不正确的，针对雷达信号识别效能评估，必须将主观因素和客观因素综合起来考虑。仿真得出了以客观权重为主，主观权重为辅时能够准确地进行雷达信号识别效能评估的结论。

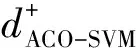
5 结束语

雷达信号识别效能评估对于电子对抗作战具有重要的现实意义，以往的评估方法存在指标选取不合理、权重设置单一和评估排序不合理的问题。为此，本文提出了基于IAHP-Entropy-I2TOPSIS模型改进的雷达信号识别效能评估方法。该方法主要对评估指标的建立、指标权重的确定和相对贴近度的计算进行了改进。将此方法应用于雷达信号识别效能评估中，通过仿真对5种识别算法的识别结果进行了评估，仿真得出了以客观权重为主，主观权重为辅时能够准确地进行雷达信号识别效能评估的结论，同时验证了所提方法可以解决原有方法存在的问题，是一种合理可行的评估方法。

[1] 徐 璟，何明浩，陈昌孝, 等. 雷达辐射源信号识别结果评估方法研究[J]. 电波科学学报，2014，29(2)：300-304. XU Jing, HE Minghao, CHEN Changxiao, et al. Performance evaluation method for radar emitter signals recognition[J]. Chinese Journal of Radio Science，2014，29(2)：300-304.

[2] XU Jing, HE Minghao, HAN Jun, et al. Estimating the stability of characteristic parameters based on single element analysis of variance[C]//2012 IEEE 11th International Conference on Signal Processing. [S.l.]: IEEE Press, 2012：1804-1807.

[3] 徐 璟, 何明浩, 陈昌孝, 等. 基于理想排序的雷达信号效能评估方法[J]. 电波科学学报, 2015, 30(3): 554-559. XU Jing, HE Minghao, CHEN Changxiao, et al. Effectiveness evalluation of signal recognition based on AHP-I2TOPSLS[J]. Chinese Journal of Radio Science, 2015, 30(3): 554-559.

[4] 徐 璟，何明浩，韩 俊. 基于AIT方法的雷达辐射源信号识别效能评估[J]. 空军预警学院学报，2014，28(4)：243-245. XU Jing, HE Minghao, HAN Jun. Effectiveness assessment of radar emitter signal recognition based on AHP-interval-TOPSIS[J]. Journal of Air Force Early Warning Academy，2014，28(4)：243-245.

[5] 徐 璟，何明浩，郁春来. 雷达辐射源信号识别效能评估的I2TOPSIS方法[J]. 信号处理，2015，31(3)：253-258. XU Jing, HE Minghao, YU Chunlai. Effectiveness evaluation of radar emitter signal recognition based on I2TOPSIS[J]. Journal of Signal Processing，2015，31(3)：253-258.

[6] 余志斌，金炜东，张葛祥. 基于峰度的自源分离算法研究与应用[J]. 电波科学学报，2008，23(1)：146-152. YU Zhibin, JIN Weidong, ZHANG Gexiang. Research and applications of blind signal separation based on kurtosis[J].Chinese Journal of Radio Science，2008，23(1)：146-152.

[7] 王 欢，何明浩，刘 锐, 等. 雷达信号识别效果的模糊综合评价研究[J]. 雷达科学与技术，2012,4(10)：372-375. WANG Huan，HE Minghao，LIU Rui, et al . Research on fuzzy comprehensive evaluation of radar signal recognition effect[J]. Radar Science and Technology，2012,4(10)：372-375.

[8] 魏 铭，徐 璟，刘 锐, 等. 雷达辐射源信号识别效果评估指标体系构建[J]. 电子信息对抗技术，2014，29(4)：58-61. WEI Ming, XU Jing, LIU Rui, et al. A construction method of radar emitter signal recognition valuation index system[J]. Electronic Information Warfare Technology，2014，29(4)：58-61.

[9] 王先甲，汪 磊. 基于马氏距离的改进型TOPSIS在供应商选择中的应用[J]. 控制与决策，2012，27(10)：1566-1570. WANG Xianjia, WANG Lei. Applications of TOPSIS improved based on mahalanobis distance in supplier selection[J]. Control and Decision，2012，27(10)：1566-1570.

[10] 刘自发，庞铖铖，魏建炜, 等. 基于IAHP和TOPSIS方法的负荷密度指标计算[J]. 电力系统自动化，2012，36(13)：56-60. LIU Zifa, PANG Chengcheng, WEI Jianwei, et al. Index calculation of load density based on IAHP and TOPSIS methods[J]. Automation of Electric Power Systems，2012，36(13)：56-60.

[11] 徐泽水，达庆利. 一种基于可能度的区间判断矩阵排序力法[J]. 中国管理科学，2003，11(1)：63-65. XU Zeshui, DA Qingli. A possibility-based method for priorities of interval judgment matrix[J]. Chinese Journal of Management Science，2003，11(1)：63-65.

[12] 韩 俊，何明浩，朱振波, 等. 基于复杂度特征的未知雷达辐射源信号分选[J]. 电子与信息学报，2009，31(11)：2552-2555. HAN Jun, HE Minghao, ZHU Zhenbo, et al. Sorting unknown radar emitter signal based on the complexity characteristics[J]. Journal of Electronic & Information Technology, 2009，31(11)：2552-2555.

[13] 徐 璟，何明浩，冒 燕, 等. 基于优化算法的雷达辐射源信号识别方法及性能[J]. 现代雷达，2014，36(10)：33-37. XU Jing, HE Minghao, MAO Yan, et al. Radar emitter recognition method based on optimization algorithm and performance[J]. Modern Radar, 2014,36(10)：33-37.

张 强 男，1991年生，硕士研究生。研究方向为电子对抗理论与技术。

王红卫 男，1974年生，副教授。研究方向为电子对抗理论与技术。

陈 游 男，1983年生，讲师。研究方向为电子对抗理论与技术。

An Improved Effectiveness Evaluation Method of Radar Signal Recognition

ZHANG Qiang，WANG Hongwei，CHEN You

(Aeronautics and Astronautics Engineering College, Air Force Engineering University, Xi′an 710038, China)

In order to solve the problems of radar signal recognition methods in fuzzy evaluation index selection, single method for index weight determination and unreasonable assessment order, an improved radar signal recognition evaluation method based on IAHP-Entropy-I2TOPSIS model is put forward. The method builds tree viewer evaluation indexes system based on measurement of recognition rate. In this model, the subject and object weight are calculated by IAHP and Entropy method. The linear combination method is used to determine the comprehensive weight. ITOPSIS method is optimized by using the method of inclination measurement for interval multi-attribute decision-making. The optimization method is I2TOPSIS, which is used to evaluate and order. Finally, the results of case simulation show the validity of the proposed method.

radar signal; effectiveness evaluation; evaluation index; interval; comprehensive weight

10.16592/ j.cnki.1004-7859.2016.11.001

航空科学基金资助项目(20162096019、20145596025)

张强 Email：zjslwdyx@163.com

2016-08-25

2016-10-23

TN971

A

1004-7859(2016)11-0001-06