基于实测数据处理的统计优化反卷积实波束锐化算法

黄柏圣，柳兆峰

(1. 南京电子技术研究所， 南京 210039； 2. 解放军61922部队， 北京 100094)



·信号处理·

基于实测数据处理的统计优化反卷积实波束锐化算法

黄柏圣1，柳兆峰2

(1. 南京电子技术研究所， 南京 210039； 2. 解放军61922部队， 北京 100094)

由于实波束地图方位分辨率低，从中很难分离出如机场、舰船及海岸线等目标的有用信息，使得战机无法实施对地、对海火力攻击。文中提出了一种基于实测数据处理的统计优化反卷积实波束锐化算法。该算法通过运动补偿及迭代算法，对实波束地图进行锐化，以实现方位超分辨。从仿真数据分析及实测数据处理的结果可以看出，所提方法能有效提高实波束地图的方位分辨率，具有很高的工程应用价值。

实波束锐化；反卷积；方位高分辨；运动补偿

0 引 言

实孔径雷达方位分辨率受天线孔径大小的限制，分辨率不高，并且随作用距离的增加而下降。通过实孔径雷达波束锐化算法能提高机载雷达前向探测地物的方位分辨能力，形成优于实波束角分辨的地物图像，可以弥补合成孔径雷达(SAR)和多普勒波束锐化(DBS)难以实现正前视成像的不足，在空投、地形规避、武器制导及飞机着陆引导等领域具有广泛的应用前景[1-4]。

本文提出了一种基于实测数据处理的统计优化反卷积实波束锐化算法，该算法通过前视雷达回波模型的建立、运动补偿及迭代优化算法，对实波束地图进行锐化，以实现方位超分辨。通过对仿真和实测数据的处理，验证了算法的有效性和稳健性。

1 基于统计优化波束锐化算法建模

1.1 雷达前视成像回波模型

雷达前视成像几何模型能清晰地表明雷达飞行过程中被照射目标与雷达间的几何关系，根据几何关系，得到目标的照射时间，进而提出距离走动跨距离分辨单元的判据，为成像系统设计提供理论基础。

如图1所示，点目标P到雷达的斜距为R0，θ0为扫描角，φ为俯仰角，v为载机的速度，t为方位向时间，经过时间t之后，载机从A到达B，此时雷达到目标的斜距为

(1)

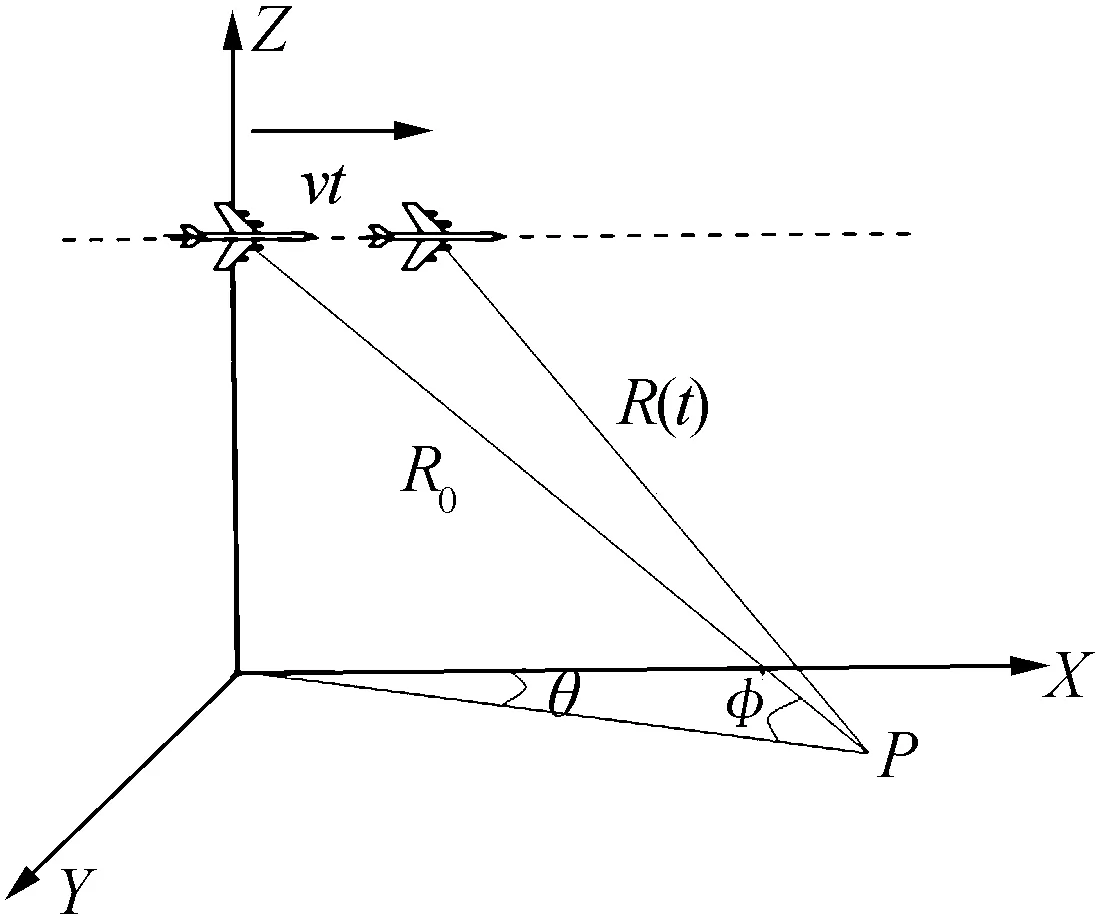
图1 机载雷达前视成像几何示意图

在t=0时对上式进行幂级数展开，有

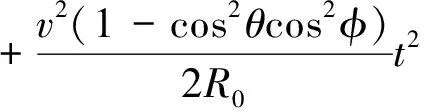
(2)

雷达成像就是从回波信号中提取目标的后向散射系数σ的二维分布，下面给出了前视雷达回波信号的模型，设雷达发射的是线性调频脉冲

St(τ)=wr(τ)exp{j2πf0τ+jπKrτ2}

(3)

式中：Kr为调频斜率；τ为距离向时间；f0为载频；wr(τ)为脉冲包络，通常近似为矩形，如下式所示

(4)

式中：Tr为脉冲持续时间。则距离向的回波信号为

(5)

式中：A0为点目标的散射幅度，距离向回波信号经去载频及距离向脉冲压缩之后的表达式为

(6)

雷达接收到的目标方位向的回波信号可以看作目标反射率分布函数的方位采样序列f(θ)与天线波束方位采样序列h(θ)进行线性卷积的结果，即

g(θ)=f(θ)*h(θ)

(7)

式中：g(θ)为雷达的方位向回波信号。则整个前视雷达的回波信号可以写为

(8)

1.2 点目标波束覆盖时间

若雷达静止不动，则一点目标的波束覆盖时间为波束宽度除以扫描速度，而当雷达运动的时候，当天线处于机械扫描状态时，天线扫描方向不同，点目标的照射时间就不一样，下面分别分析了在图2所示的几何关系(XOY平面)中，天线顺时针扫描和逆时针扫描对照射时间的影响。

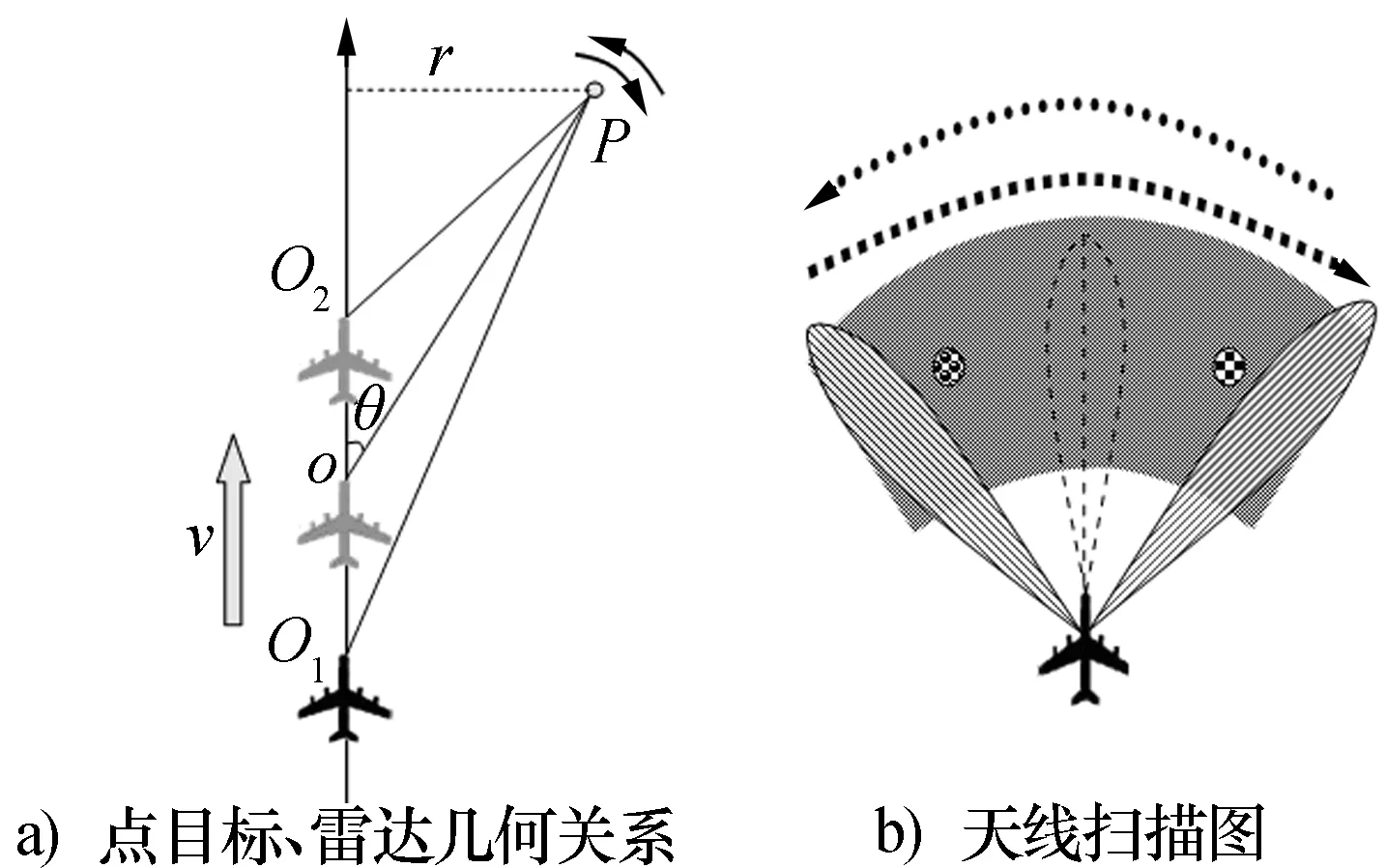
图2 点目标、雷达几何关系及天线扫描图

对点目标P,当雷达天线逆时针扫描时，此时天线扫描方向与雷达运动方向一致，载机速度为v，波束宽度为β，扫描速度为θv，点目标P到航线在X轴投影的垂直距离为r，波束视线与正前方向的夹角为θ。当雷达位于o1时,波束前沿刚照射到目标P，此时目标离雷达的斜距最长；当雷达位于o2时，波束后沿照射到目标P，此时目标P离雷达的斜距最短，此时点目标的波束驻留时间为

(9)

当雷达天线顺时针扫描，此时天线扫描方向与雷达运动方向相反，同上文的推导过程，此时点目标的波束驻留时间为

(10)

1.3 距离走动判据

载机在飞行的过程中，目标相对飞机的斜距是变化的，若在波束驻留时间内，目标斜距的变化超过一个距离分辨单元，导致方位向和距离向数据耦合，在方位向波束锐化的时候不能正确得提取方位向数据，导致波束锐化算法迭代后不能得到最优的估计值，从而影响算法的锐化性能。因此，应该避免这种情况的发生[5-6]。当天线扫描方向与雷达载机飞行方向一致的时候，距离走动差为

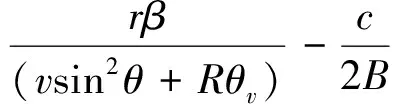
(11)

当天线扫描方向与雷达载机飞行方向相反的时候，距离走动差为

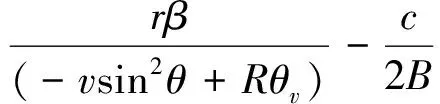
(12)

d>0，可以忽略目标距离走动；d<0，不能忽略目标距离走动。根据式(11)和式(12)，得到目标的距离走动量和波束宽度、载机飞行速度、天线扫描速度、天线俯仰角等因素有关。当其他参数一定时，天线扫描速度越大，距离走动量越小，目标回波发生跨距离门的可能性越小，设置合适的系统参数，就可以避免发生目标的回波距离走动。

1.4 运动补偿

雷达在运动的时候，在距离维，目标在波束覆盖时间内，若由雷达平台运动导致的斜距变化小于一个距离分辨单元，则可以忽略距离走动的影响，即忽略载机运动对距离向产生的影响；在方位向，雷达平台的运动会导致目标被覆盖时间的改变。

图3所示为XOY平面内平台运动导致的目标角度变化示意图，根据图3所示的几何关系，得到

(13)

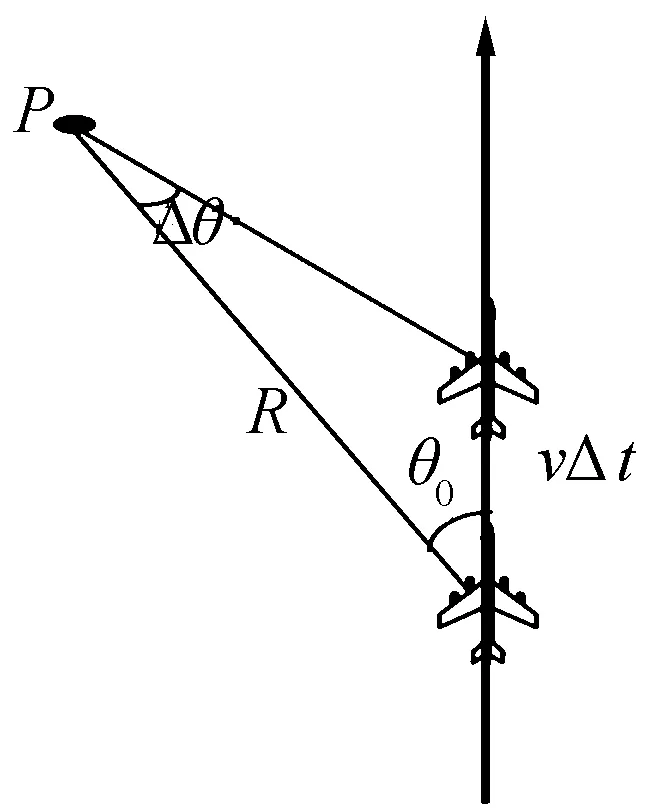
图3 平台运动角度变化示意图

将上式泰勒展开，忽略二阶项及二阶以上高次项，可得

(14)

假设雷达波束在第k次时间采样照射到目标，则有

(15)

式中：θv为天线的扫描速度。假设雷达波束在第n次时间采样离开目标，则有

(16)

(17)

(18)

于是，雷达波束覆盖目标的角度范围为

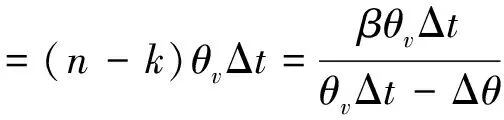
(19)

由上式可以看出，当Δθ=0时，有Δφ=β，即雷达波束覆盖目标的角度范围等于雷达波束宽度；当Δθ>0时，有Δφ>β，即雷达波束覆盖目标的角度范围大于雷达波束宽度，当Δθ<0时，有Δφ<β，即雷达波束覆盖目标的角度范围小于雷达波束宽度[7]。故照射时间内目标所处角度单元的中心为

(20)

将式(13)代入上式，并泰勒展开，忽略二阶及二阶以上高次项，可得

(21)

从上式可以看出，雷达平台运动导致的方位向角度的变化是受斜距R变化影响的，具有空变性，而这个变化可以写成一个随斜距R变化的变化因子与原始角度相乘的形式，如下式所示

θ′≈f(R)θ0

(22)

因此，雷达平台运动导致的方位向角度的变化可以看成目标的原始角度进行了受斜距影响的尺度缩放，所以，将所得目标图像在方位向按式(20)进行尺度变换即可完成运动补偿[8-10]。

从图4a)可以看出，若天线顺时针扫描，此时雷达运动方向与天线扫描方向一致，目标A的照射时间变短，且波束照射目标A的时间先于雷达静止时的到达时间，波束离开目标A的时间也先于雷达静止时的离开时间；若天线逆时针扫描，此时雷达运动方向与天线扫描方向相反，目标的照射时间变长，且波束照射目标A的时间迟于雷达静止时的到达时间，波束离开目标A的时间也迟于雷达静止时的离开时间。

目标B的结论正好和目标A相反，见图4c)。

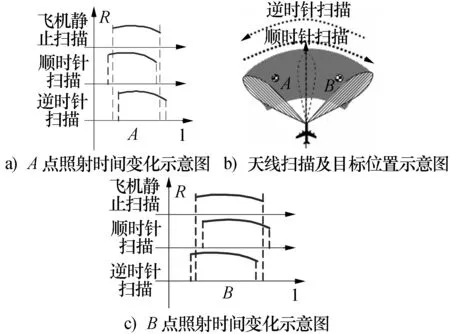
图4 平台运动对目标方位向影响示意图

2 算法流程

图5所示为算法的流程图，先对目标的回波数据进行距离向脉冲压缩，再用基于统计优化的波束锐化算法对回波方位向进行处理，经方位向运动补偿后，最后对扫描区域进行成像显示。

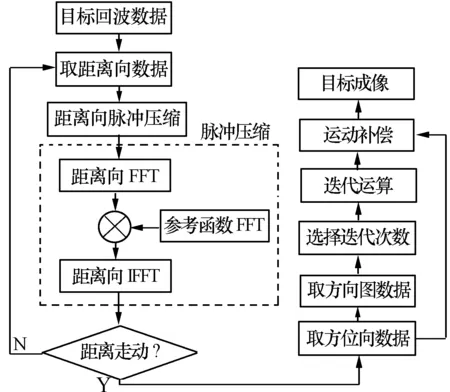
图5 算法流程图

3 仿真分析

3.1 点目标仿真分析

仿真一：仿真参数为：平台速度:340 m/s；目数：18；SNR：20 dB；距离分辨率：5 m；扫描范围：±15°；斜距：6 km；作用距离：8 km；波束宽度：3°；扫描速度：30°/s。图6a)为原始数据场景；图6b)为实波束数据，目标在距离向有走动；图6c)为最终波束锐化结果。

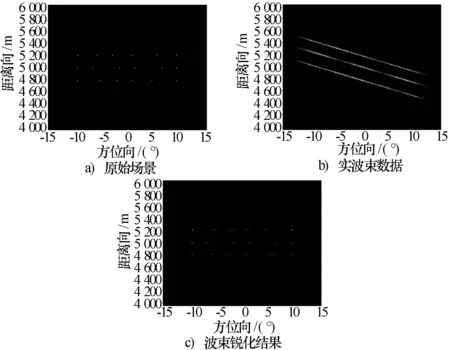
图6 平台速度为340 m/s时的仿真结果

仿真二：仿真参数：波束宽度：4°；扫描范围：±10°；其他与仿真一基本相同。图7a)为实波束结果；图7b)为波束锐化结果。从仿真结果可以得出：波束宽度为4°的天线方向图与间距为0.38°的两个目标(如图中两条虚线所示)，可以看出，波束锐化后，明显区分开了相距很近的两点目标，波束锐化比为4/0.38=10.5倍。

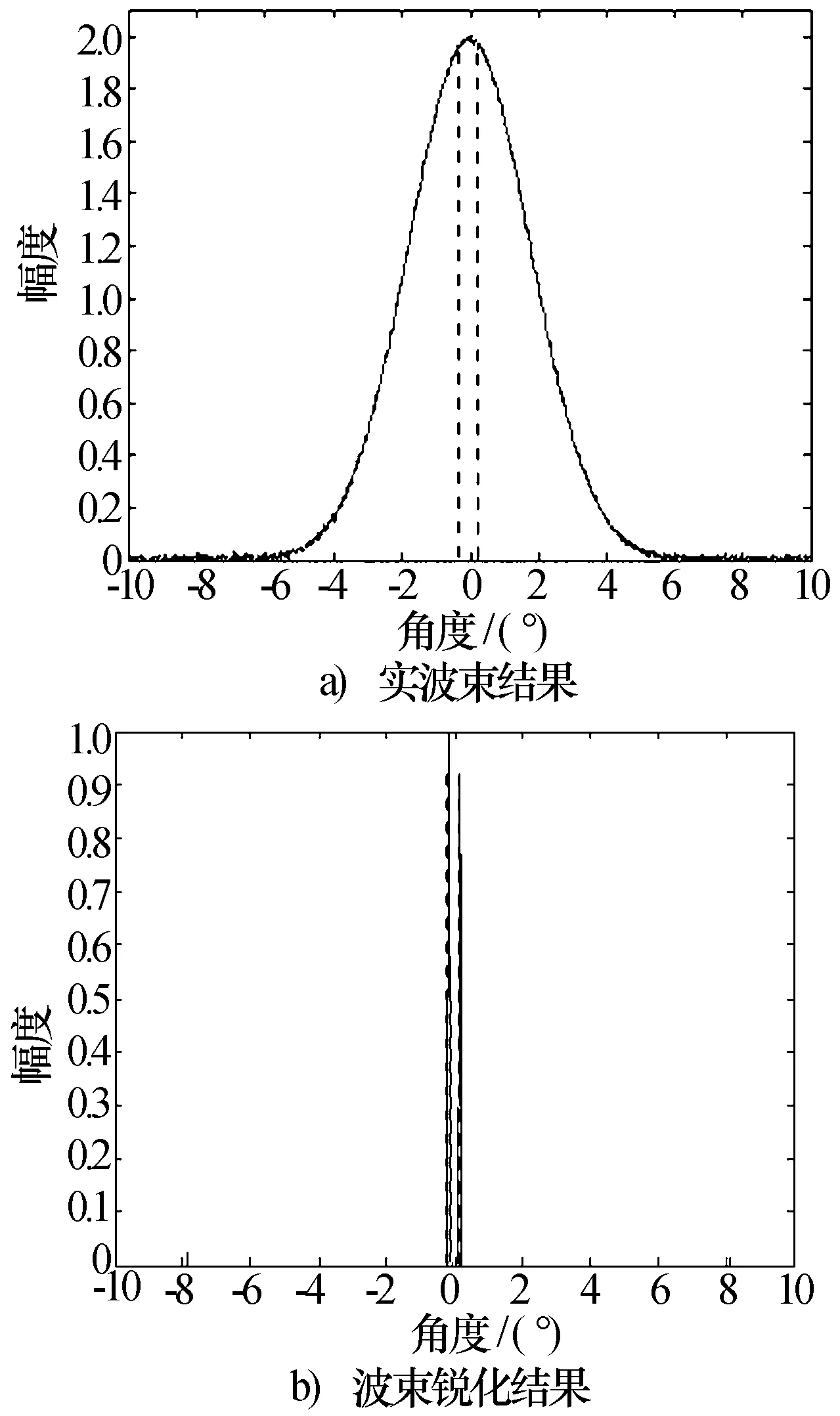
图7 分辨率提高仿真结果

3.2 面目标仿真

仿真参数如下：工作频率：30.75GHz；平台速度：340 m/s；扇区宽度：±30°；波束宽度：3°；作用距离：5 km；扫描速度：60 °/s。

图8为原始场景图,图9为距离向3.0 km～3.7 km、方位向-30°～+30°的成像场景里面11个点目标的实孔径图(将方位向角度已转换成方位向距离)，从该图上很难分辨出11个点目标，锐化后的成像结果见图10。从该图上能分辨出11个点目标，即实孔径成像不能分辨的点目标经波束锐化算法锐化后能容易地被分辨。

图8 原始场景

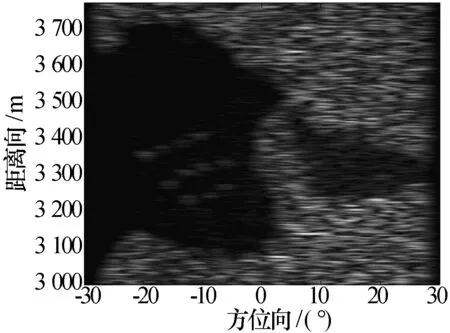
图9 实波束数据

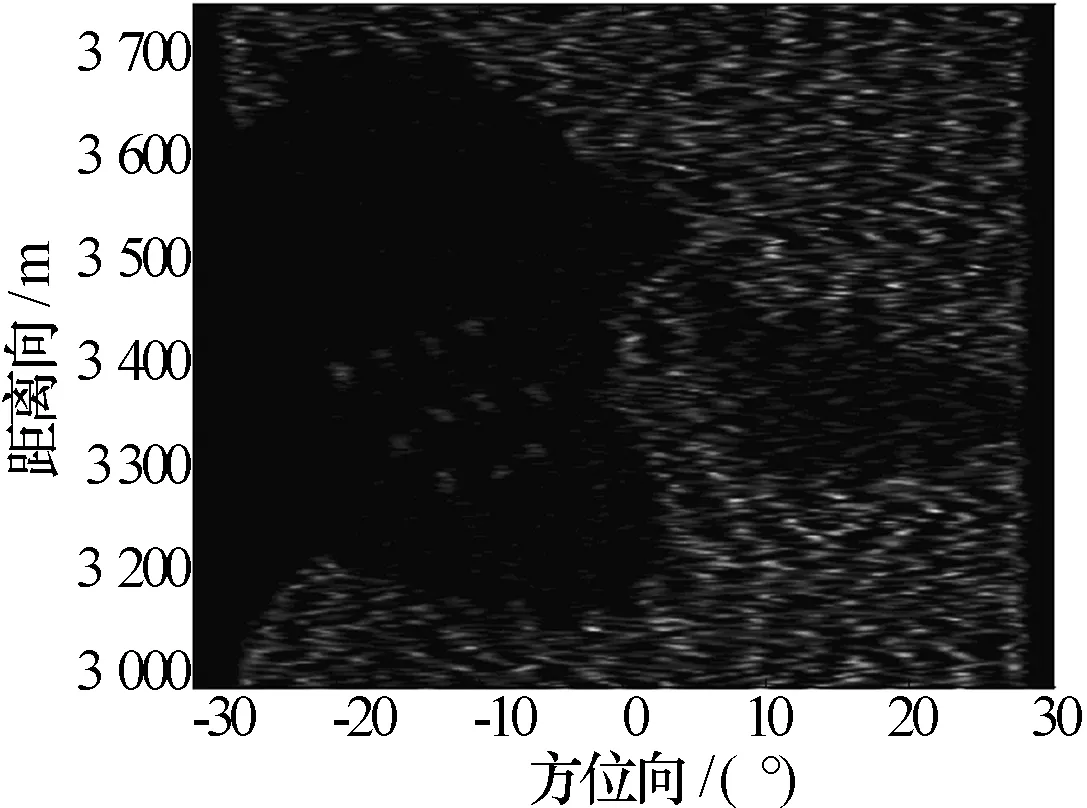
图10 波束锐化结果

4 实测数据处理

图11为某单脉冲雷达数据处理结果，图 11a)、图11b)分别为单脉冲雷达和通道实孔径成像和锐化后的图像，与实孔径图像相比，锐化后图像的边缘及目标细节信息比较清晰。

图11 实测数据和通道处理结果

5 结束语

从仿真数据分析及实测数据处理的结果可以看出：(1) 基于统计优化的反卷积锐化方法对仿真和实测数据均有效，能够实现5倍以上锐化比；(2) 数据应具有足够的信噪比，一般SNR>5 dB，需要细节分辨时要求10 dB以上；(3) 保证足够的方位采样率。对一个单点目标主瓣至少保证8个采样点；(4) 扫描场景大小应与波束扫描速度和脉冲重复频率相适应，以保证波束对目标足够的驻留时间；(5) 反卷积虽然需要利用迭代完成，但是对于一定的场景，可经过优化减少迭代次数，以加快处理时间。

[1] 丁广义，杨建宇，张卫华. 改进实孔径角分辨率的广义逆滤波方法[J]. 电子学报，1993, 21(9): 15-19. DIN Guangyi, YANG Jianyu, ZHANG Weihua. Improvement of angular resolution of real aperture radar via generalized inverse filtering[J]. Journal of Electronics, 1993, 21(9): 15-19.

[2] 朱 力，王盛利，单荣光. 去卷积实现雷达方位超分辨方法的试验研究[J]. 现代雷达，1998, 20(3): 57-60. ZHU Li, WANG Shengli, SHAN Rongguang. Experimental study on azimuth super resolution using deconvolution method[J]. Modern Radar, 1998, 20(3): 57-60.

[3] BERENSTEIN C A, PATRICK E V. Exact deconvolution for multiple convolution operators-an overiew, plus performance characterizations for imaging sensors[J]. Proceedings of the IEEE,1978(4): 723-734.

[4] 陈洪猛，李 明. 基于多帧数据联合处理的机载单通道雷达贝叶斯前视成像[J]. 电子与信息学报，2015(10)：27-32. Chen Hongmeng, LI Ming. Bayesian forward-looking imaging for airborne single-channel radar based on combined multiple frames data[J]. Journal of Electronics & Information Technology, 2015(10)：27-32.

[5] 包 敏, 周 鹏, 史 林. 双天线前视弹载SAR 解模糊算法研究[J]. 电子与信息学报, 2013, 35(12): 2857-2862. BAO Min, ZHOU Peng, SHI Lin. Study on deambiguity algorithm for double antenna forward looking missile borne SAR[J]. Journal of Electronic & Information Technology, 2013, 35(12): 2857-2862.

[6] LI W, YANG J, HUANG Y. Keystone transform-based space-variant range migration correction for airborne forward-looking scanning radar[J]. Electronics Letters, 2012,48(2): 121-122.

[7] IVERSON D. Beam sharpening via multikernal deconvolution[C]// 2001 CIE International Conference on Radar. [S.l.]: IEEE Press, 2001: 693-697.

[8] 白文斯密，马 洪，常 军. 一种利用多核解卷积提高雷达角分辨率的方法[J]. 电讯技术，2008(12): 43-46. BAI Wen Simi, MA Hong, CHANG Jun. Method of improving radar angular resolution via multikernal deconvolution[J]. Telecommunication Enginerring, 2008(12): 43-46.

[9] WANG R, DENG Y K, LOFFELD O. Processing the azimuth-variant bistatic SAR data by using monostatic imaging algorithms based on 2-D principle of stationary phase[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3504-3520.

[10] WANG R, DENG Y K, ZHANG Z Z. Double-channel bistatic SAR system with spaceborne illuminator for 2-D and 3-D SAR remote sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(8): 4496-4507.

黄柏圣 男，1978年生，博士，高级工程师。研究方向为机载雷达总体系统技术。

柳兆峰 男，1975年生，副研究员。研究方向为作战模拟等。

A Statistical Optimum Deconvolution Real Beam Sharpening Algorithm Based on Real Measured Data Processing

HUANG Baisheng1，LIU Zhaofeng2

(1. Nanjing Research Institute of Electronics Technology, Nanjing 210039, China)(2. The Unit 61922 of PLA, Beijing 100094, China)

Because the real beam map of azimuth resolution is low, from which it was difficult to separate the useful information such as airport, ship and coast line target, which can not be implemented to ground and sea attack fighter. This paper presents a statistical optimum deconvolution real beam sharpening algorithm based on real measured data processing, through the algorithm of motion compensation and iterative algorithm, sharpening the real beam map, to achieve azimuth super resolution, from the simulation data analysis and real measure data processing can be seen from the results, the proposed method can effectively improve the real beam map azimuth resolution, with a strong engineering application value.

real beam sharpening; deconvolution; azimuth super resolution; motion compensation

10.16592/ j.cnki.1004-7859.2016.11.010

黄柏圣 Email：huangbaisheng@163.com

2016-08-24

2016-10-28

TN957

A

1004-7859(2016)11-0044-05