奇偶阵元数均匀圆阵测向性能研究

谈文韬，林 明，黎仁刚

(1. 江苏科技大学 电子信息学院, 江苏 镇江 212003)(2. 中船重工集团七二三研究所， 江苏 扬州 225101)



·信号处理·

奇偶阵元数均匀圆阵测向性能研究

谈文韬1，林 明1，黎仁刚2

(1. 江苏科技大学 电子信息学院, 江苏 镇江 212003)(2. 中船重工集团七二三研究所， 江苏 扬州 225101)

均匀圆阵比起其他形状的阵列，更符合电子侦察测向接收机的应用需求。文中采用将均匀圆阵投影为随入射角变化的非均匀线阵的方式，分析了奇偶阵元数均匀圆阵中的波程差特点，给出了对应的半径选取公式，并提出采用信号矢量相关系数表示测向误差变化趋势的方法。分析了两种不同阵列中各向等效性、测向精度、相位模糊与对阵元位置误差敏感度等特点，通过仿真验证了推论与公式的有效性。在工程应用方面，文中结论对均匀圆阵布阵具有较高的参考价值。

均匀圆阵；测向；奇偶阵元数；多信号分类算法

0 引 言

有针对性的电磁干扰、情报截获、精准打击等战略举措离不开对辐射源目标的精确定位，军事领域的迫切需求，推进了超分辨测向技术在电子战中的应用。应用于舰船的测向系统的实时性要求与隐蔽性要求，限制了天线阵的阵元数与尺寸形状的选择。比起均匀线阵与均匀矩形阵，在相同孔径渡越、低阵元数的条件下，均匀圆阵(UCA)具有最优的尺寸、全方位的测向能力，广泛应用于不同系统[1-2]；具有圆对称性，在阵元数较多时，各向分辨能力近似相等；是一种平面阵，具有二维空间角的测向能力。因此，均匀圆阵更适用于电子侦察测向接收机。但现在对天线阵形的研究热点集中在大型稀疏阵列的配置[3-4]，对低阵元数阵列布阵研究发表文章较少。

由于电子侦察中，待测目标信号的频率高达18 GHz，信号波长短，为了保证测向的正确性，必须牺牲天线阵孔径来避免相位模糊[5-6]。考虑计算量，稳健性以及对阵列结构依赖性等因素，Schmidt等[7]提出的多信号分类(MUSIC )算法及其改进算法一直是工程化应用的优先选择。针对上述情况，本文根据均匀圆阵的结构特点将其投影为入射方向上的非均匀线阵，参考非均匀线阵分析方法[8-10]，确定均匀圆阵半径选取范围；并以MUSIC算法为例，深入研究了奇偶阵元数均匀圆阵对测向性能的影响。

1 MUSIC算法

我们假设一个半径为R的M元均匀圆阵的所有阵元均位于坐标系X-Y平面内，第k-1个阵元坐标为(xk,yk,0)，第i个窄带信号波长为λ，来波方向为(θi, φi)，如图1所示，则第k-1个阵元到圆心(即原点)的波程差Δrik为

Δrik=(xkcosθi+yksinθi)sinφi

(1)

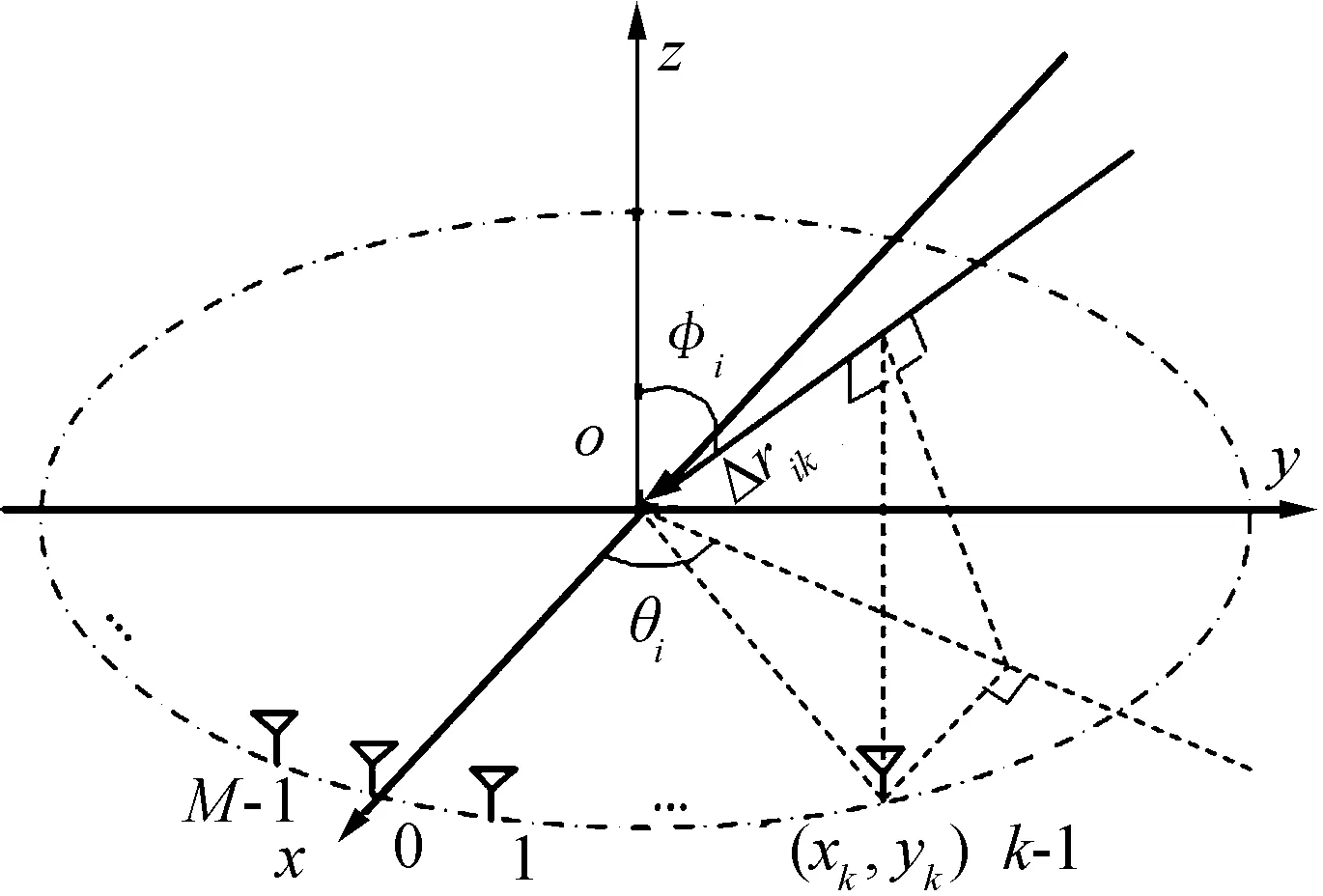
图1 均匀圆阵

存在P个入射信号均匀圆阵的接收模型可表示为

(2)

A=[α1, α2, …, αP]

(3)

s(t)=[s1(t), s2(t), …,sP(t)]

(4)

x(t)=As(t)+n(t)

(5)

式中：s(t)表示P个入射信号组成的矩阵；x(t)表示数据接收矩阵；αi(θi,φi)表示方向矢量；A表示均匀圆阵阵列流形。

MUSIC算法基本原理为

Rxx= E[x(t)x(t)H]=ARssAH+σ2IN=

UsΣsVs+UnΣnVn

(6)

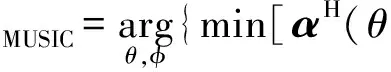
(7)

(8)

式中：Rxx表示接收数据的协方差矩阵；Rss表示入射信号协方差矩阵；σ2表示噪声功率；IN表示单位矩阵；Us、Un分别为奇异值分解后得到的信号子空间与噪声子空间；上标^表示极大似然估计；Pmusic为空间谱。

2 奇偶UCA性能分析

2.1 抗相位模糊能力

令任意两阵元间的波程差dr(θi,φi,m,n)为

dr(θi,φi,m,n)=Δrim-Δrin

(9)

当dr(θi,φi,m,n)>λi时，即产生相位模糊。将均匀圆阵各阵元投影到入射方向，得到一个随入射方向变动的非均匀线阵。需要保证在任意入射方向上投影出的非均匀线阵，其最小间隔总是小于信号波长，模糊谱峰对测向结果影响较小，即

(10)

由式(1)、式(9)可知，在方向角φi相同时，水平入射(sinφi=1)信号的波程差最长，且投影出的非均匀线阵随方向角不同周期变化。因此，只需要讨论水平入射信号对应投影线阵的不同情况。

在MUSIC算法中，阵元的最小间隔越大模糊谱峰峰值就越大。但在均匀圆阵中，阵元间隔随着入射波方向变化，因此算法性能受到最小间隔最大值的影响。根据来波方向不同，入射方向上的第k个阵元投影间隔分别为

(11)

(12)

由图2阵元间隔变化曲线可得出，当M为奇数时，对着阵元入射，投影点重合为(M+1)/2个；当M为偶数时，对着相邻阵元连线中点入射，投影点重合为M/2个，此时投影线阵的非零最小间隔的值最大，且取得该最大值时k=1。

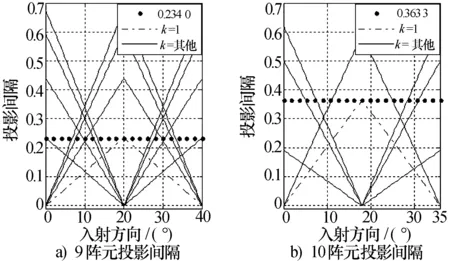
图2 投影间隔随入射方向变化曲线

根据图2的分析结果，以及使最小间隔最大值尽可能小的布阵原则，由式(10)～式(12)可求得半径的选取关系

(13)

选取半径时，按式(13)等比例缩放，即能使对应的奇数阵与偶数阵有近似的抗相位模糊的性能。

2.2 测向精度

入射信号为18 GHz时，阵元数不同的均匀圆阵半径可由式(6)计算得到(见表1)，根据半径的值可以明显看出，奇数UCA的最大半径可以比偶数阵半径大得多，也即在阵元数接近时，奇数UCA的最大天线孔径要大于偶数UCA最大天线孔径，测向精度更高。

表1 18 GHz入射UCA的最大半径 cm

M789101112Rmax4．42663．07967．12394．587910．49896．4395

2.3 各向等效性

假设入射信号为中心频率18GHz窄带信号，以6 cm为半径，画阵元数分别为7～10的均匀圆阵方向图，如图3所示。可以看出，奇数UCA比起偶数UCA，方向图更接近球形，因相位模糊产生的波束密度大，幅值小。这说明在阵元数接近，半径相同的情况下，奇数UCA的各向等效性优于偶数UCA。

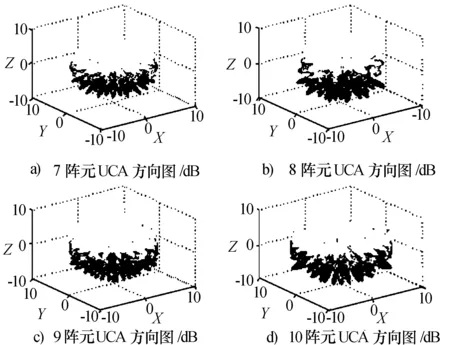
图3 7～10阵元UCA方向图

2.4 阵列误差敏感度

均匀圆阵在空间内分布，其位置误差可以转换为在入射方向上的波程差误差，波程差误差模型为

τik= Δxkcosθisinφi+Δyksinθisinφi+Δzkcosφi=

(Δxk,Δyk,Δzk)·(cosθisinφi,sinθisinφi,cosφi)

(14)

式中：Δxk、Δyk、Δzk分别为坐标轴方向上的阵列误差值。此处多个阵元间误差正负不同、方向不同，误差的增益与抵消同时存在，难以进行直观地表述。从式(14)可以看出，当单个阵元误差模长一定、方向与信号入射方向一致时，在信号入射方向上的投影最长，也即波程差误差最大。

考虑单信号入射的极端情况，此时仅需考虑投影非均匀线阵上的相位误差，则有

(15)

式中：α(Δr,τ)是带有误差测得的方向矢量，τ为投影阵元位置误差矢量。

由MUSIC算法的定义可知，空间谱实质上是一种对来波方向接收流形的正交性分析所得出的值，所以在理想无噪声时，信号子空间与真实阵列流形在N维空间内是同向平行的，所以两个向量存在如下关系

Us=αr=Us1α(Δr,τ)/α1

(16)

式中：α1、Us1分别为真实阵列流形与信号子空间矢量的第一个元素，经过相位对齐后，向量的积为实数。而在扫描过程中，使用的流形是理想的，且阵元位置变化仅引起阵列流形相位的变化，并不影响幅度，所以

Us≠αi=Us1α(Δr,0)/α1

(17)

(18)

(19)

式中：αr、αi分别表示真实阵列流形与理想阵列流形；αi1表示理想阵列流形矢量第一个元素。理想阵列流形与真实阵列流形在信号子空间构成的复平面上的投影不同，可以将αr、αi分别理解为一个代表阵列信息的信号，式(19)值代表量信号的互相关函数，该值与误差在来波方向上的投影有关。

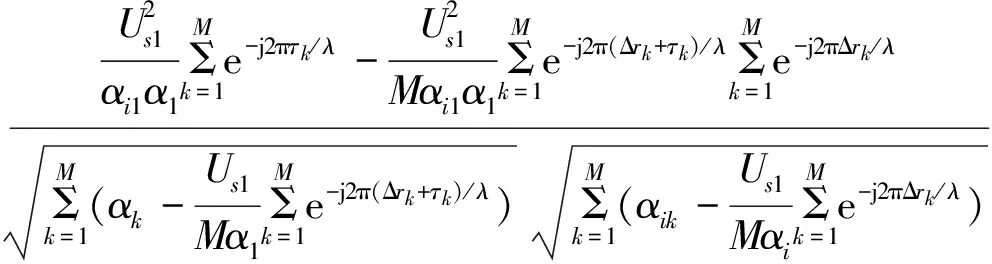
(20)

式中：ρ为两个向量的相关系数，可以通过该值反应对阵列位置误差的敏感程度，ρ的值越小产生大测向误差的概率越高。

相关系数的值受来波方向(θi,φi)、位置误差(Δxk,Δyk,Δzk)、均匀圆阵半径R、阵元数M等3M+4个变量影响，变化关系极其复杂。ρ仅能代表测向误差的变化趋势，并不能完全代表测向精度，此处相关系数对任意阵型和多数情况下测向精度变化趋势适用。该值能够作为布阵时的最优化函数之一，具有计算量小、适用性广的优点。

3 奇偶UCA性能仿真

通过计算机仿真对上述推论进行验证：以中心频率为18 GHz、带宽为20 MHz的线性调频信号作为入射信号，采样频率为40 MHz，快拍数为32点；接收噪声为白噪声，噪声基底为-45 dB。下述试验中的蒙特卡洛试验均为100次。

试验1：抗相位模糊能力

在实际应用中，适用18 GHz信号的低阵元数UCA半径一般在5 cm～10 cm范围内，此处选取中间值10 cm作为半径。根据奇偶数阵对称特性的不同，选取奇数阵入射角度为1×360°/M，选取偶数阵入射角度为1.5×360°/M，信噪比为10 dB。

从图4中可以看出，9阵元UCA的模糊谱峰均在7 dB以内，数量较少；而10阵元UCA的模糊谱峰高达13 dB，且大于5 dB的模糊谱峰数量多，甚至影响真实谱峰的判别，在多信号入射的情况下，模糊谱峰严重影响测向结果的正确率。这说明奇数UCA的抗相位模糊特性远远强过偶数UCA。

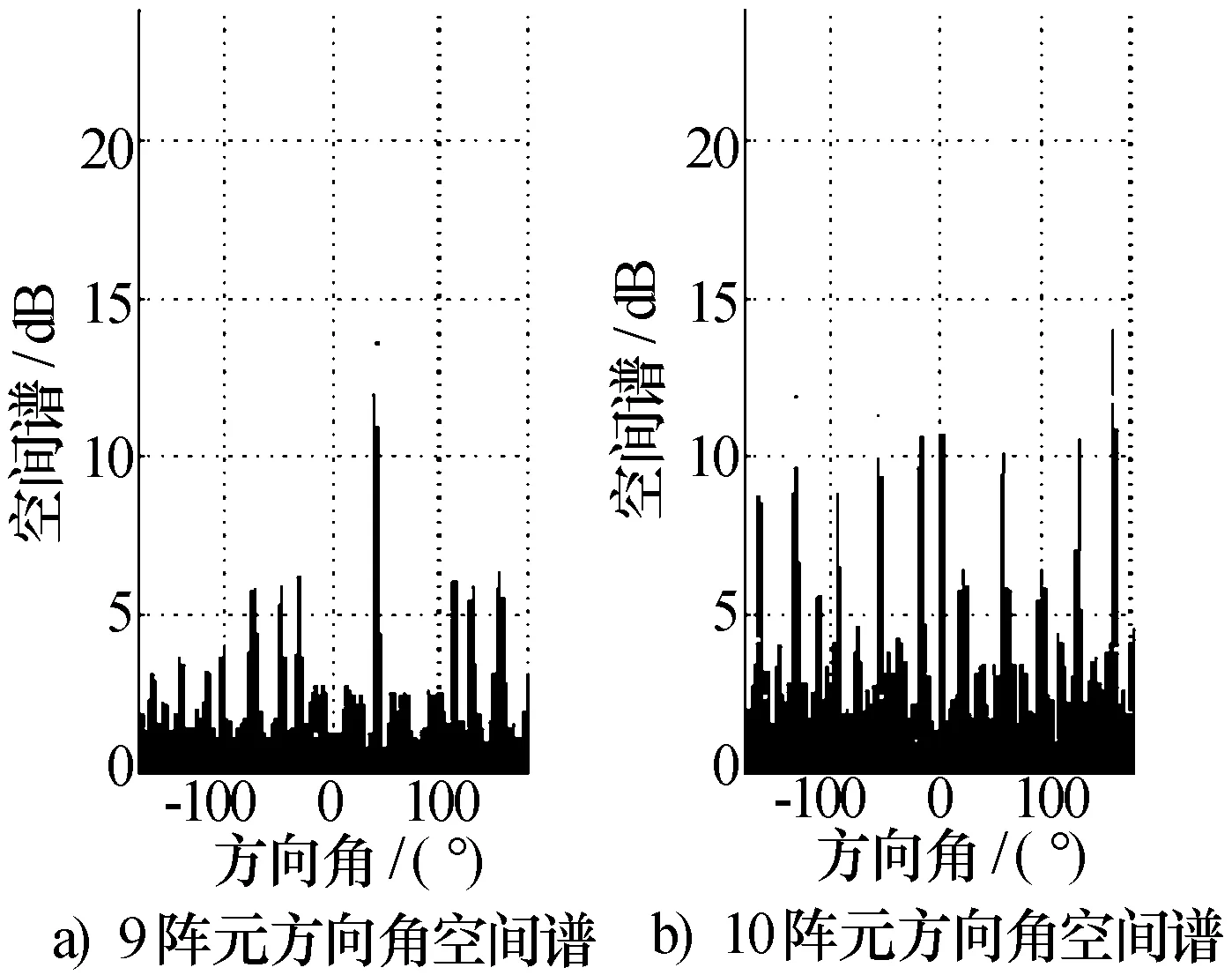
图4 9、10阵元UCA空间谱R=10 cm

再按式(13)选取均匀圆阵最大半径，9阵元为7.123 9 cm，10阵元为4.587 9 cm，进行空间谱仿真。

在图5中，奇数阵偶数阵的模糊谱峰值比较接近，所有的模糊谱峰均在7 dB以内，与真实来波方向形成的谱峰有较大的差值，这验证了式(13)的正确性。

图5 9阵元、10阵元UCA空间谱

试验2：测向精度试验

在进行阵列测向精度的比较仿真时，通常以阵列最差的测向精度作为参考。入射角选取与试验1相同：奇数阵为1×360°/M，偶数阵为1.5×360°/M。本次试验采用表1中的半径长度对7～10阵元UCA进行仿真。

从图6中可以看出，在阵元数相差1时， 偶数UCA的测向均方误差均较大。圆阵半径越大，天线孔径越大，测向精度越高。验证了选取最大半径时，奇数UCA比偶数UCA测向精度更高的优点。

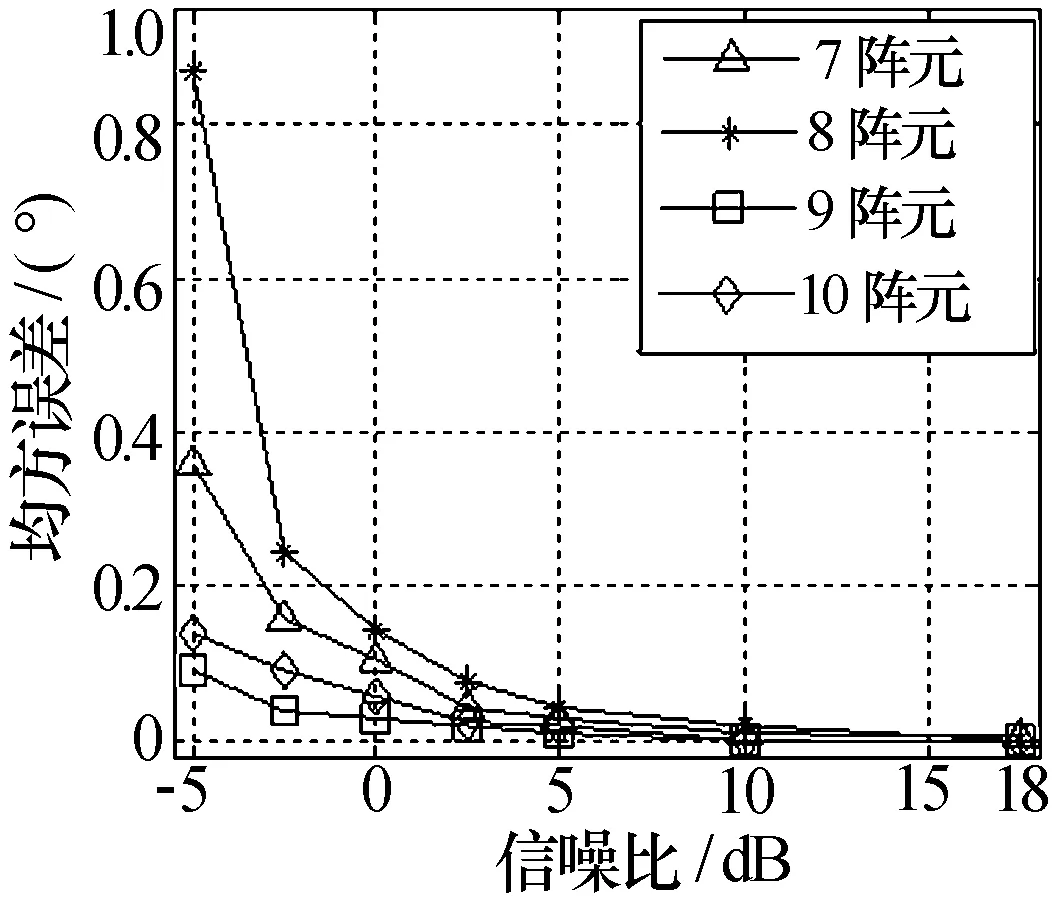
图6 7阵元～10阵元最大半径测向试验

以相同的半径对不同阵元数均匀圆阵进行仿真试验，取R=10 cm。

从图7中可以看出，在半径相同时，测向精度随着阵元数的增加而提高。这是因为阵元数多的天线阵快拍获取的数据量更大，但随着阵元增加，因数据量提升的精度越来越小，图7中9阵元、10阵元的精度曲线非常接近，已经难以区分。

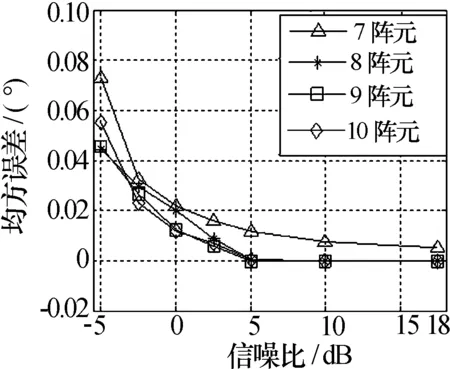
图7 7阵元～10阵元相同半径测向试验

试验3：各向等效性试验

以9阵元UCA与8阵元UCA为例，分析均匀圆阵的各向等效性。为了避免相位模糊对试验造成影响，此处为便于仿真对比，选取圆阵半径为2 cm，并不符合实际应用情况。固定俯仰角为60°，选取两个参考入射方向角，奇数阵为(-1.125,3)×360°/M，偶数阵为(-1.25,2.5)×360°/M，此时阵元在入射方向上分别具有投影间隔最均匀、投影点最少的特点。

在图8中可以明显看出：9阵元两个不同方向上的测向精度基本相同；而8阵元两个方向角的均方误差出现了明显的差值。这说明了奇数UCA比偶数UCA各向等效性更好。

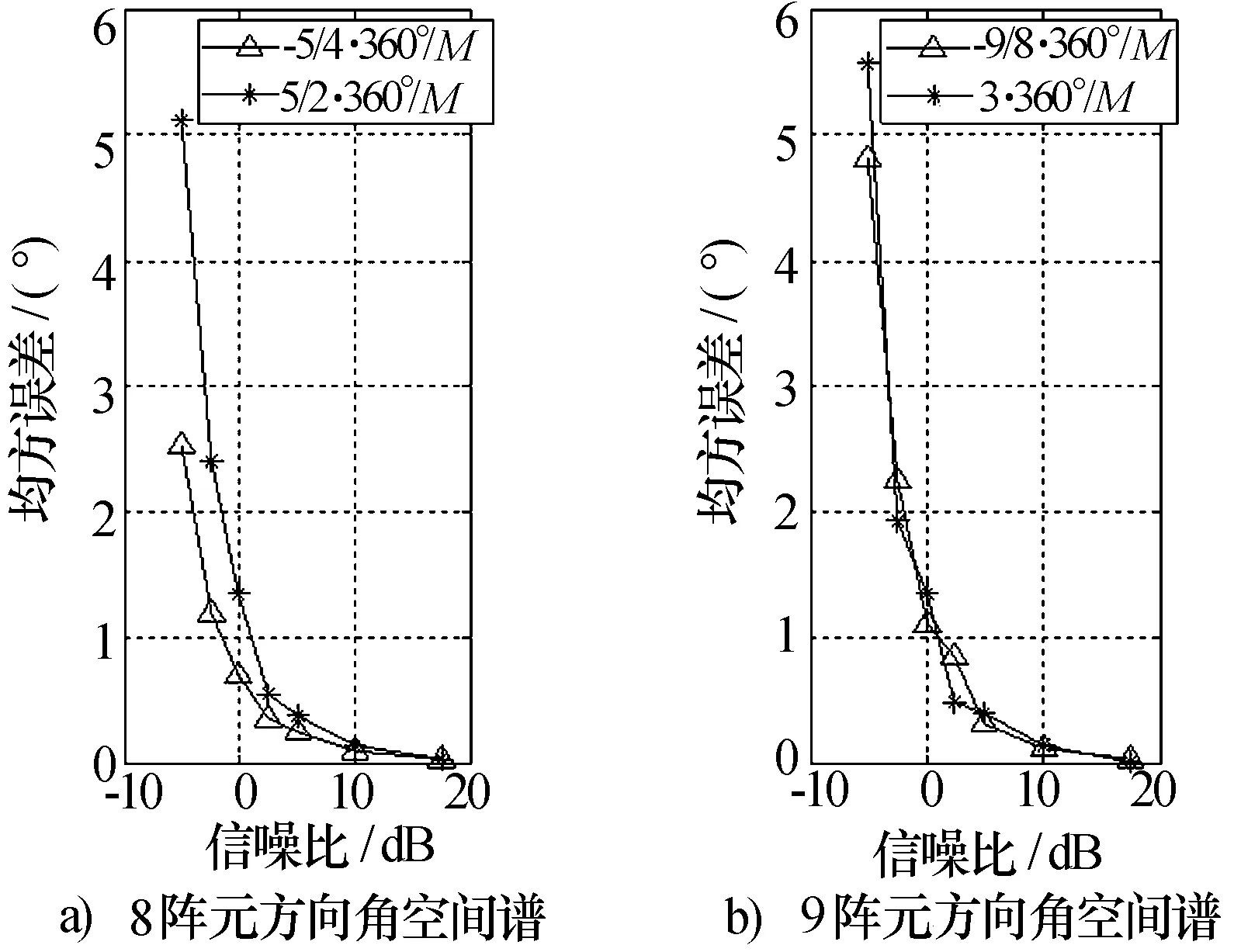
图8 8阵元、9阵元UCA各向等效性试验

试验4：位置误差敏感度试验

图9是100次试验测向结果的均方误差与相关系数ρ的关系图，测向均方误差随ρ的增加而减小，该试验说明ρ能够代表测向误差的变化趋势。

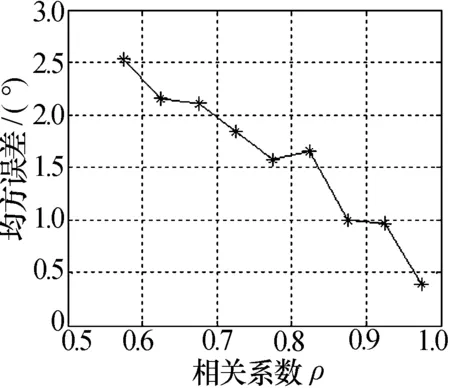
图9 误差与相关系数关系

假设单个阵元位置误差方向与来波方向相同，幅值为随机1 mm，其变量固定，则随阵元数M的增加，实际流形均值变化幅度减小，ρ单调增；随着圆阵半径增加，阵元误差占阵元间隔比例减小，ρ单调增。所以随着阵元数与圆阵半径的增加，阵列对位置误差的敏感度降低。

上述分析均是在来波方向上主峰值清晰可分辨的前提下推导得出的，在奇偶阵元数UCA对阵列误差敏感度的分析中，还需要着重考虑由位置误差引起的相位混乱问题。在非均匀线阵中，最小阵元间隔的畸变对相位影响最大，也即对空间谱结果影响最大，当最小阵元间隔大于入射信号波长时，将产生严重的相位模糊。因此，令η=λ/rmin作为相位混乱敏感度的参考标准，与式(13)类似。可以看出阵元数相差1，半径相同的奇数UCA的η值要大于偶数UCA的值。

综合考虑上述两种情况，在信号波长较长时，相位模糊影响较小，无论奇偶数UCA，阵元数少的均匀圆阵对阵列误差更敏感；在信号波长较短时，奇数UCA能拥有更大的半径，对阵列位置误差敏感度更低。

此处取各阵元误差τi的标准差为0～2(mm)，误差方向为信号入射方向，按式(13)选取半径，信噪比10 dB，入射角与试验1相同，分别对8阵元～10阵元进行仿真试验。

从图10中可以看出，在存在较大阵列位置误差时，即便按式(13)选取半径，使得奇数阵的半径大于偶数阵，但测向误差仍由阵元数目决定，阵元数目的奇偶性与圆阵半径大小对其影响较小。

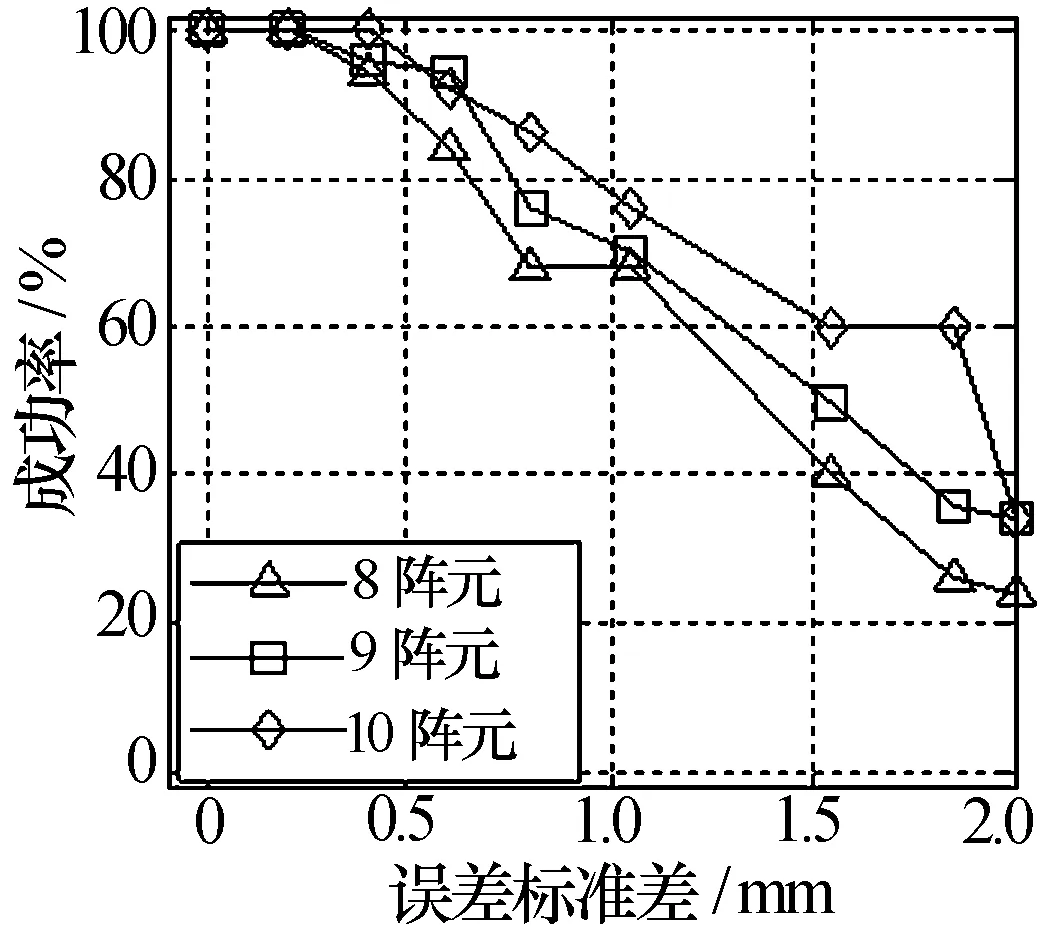
图10 8阵元～10阵元UCA阵元位置误差

4 结束语

本文将均匀圆阵投影为随方向变化的非均匀线阵，分析了均匀圆阵的波程差，提出了根据奇数UCA与偶数UCA不同特点的半径选取公式，并提出了多数情况适用的反映测向误差变化趋势的相关系数计算方法，该值对阵列布阵具有重要的参考意义。得出并验证了奇数UCA比起偶数UCA具有更好的各向等效性、更高的测向精度以及更强的抗相位模糊能力的推论，同时仿真得出了阵元数比半径对位置误差影响更大的结论。

[1] 吴奉微, 程 婷, 贾可新,等. 基于虚拟阵列变换的干涉仪测向方法[J]. 现代雷达, 2012, 34(3): 42-45. WU Fengwei, CHENG Ting, JIA Kexin, et al. Algorithm of interferometer in direction finding based on virtual array transformation[J]. Modern Radar, 2012, 34(3): 42-45.

[2] 杨延光, 黄晓涛, 张小义. 基于均匀圆阵的循环平稳信号源方位估计[J]. 现代雷达, 2005, 27(8): 35-38. YANG Yanguang, HUANG Xiaotao, ZHANG Xiaoyi. Azimuth estimation of cyclostationary signal sources based on uniform circular array[J]. Modern Radar, 2005, 27(8): 35-38.

[3] 邵 华. 稀疏阵列测向技术研究[D]. 南京: 南京理工大学. 2014. SHAO Hua. Research on direction finding techniques using a sparse array[D]. Nanjing: Nanjing University of Science & Technology, 2014.

[4] 唐宝富, 王浚海. 稀疏阵列天线结构设计[J]. 电子机械工程, 2004, 20(4): 22-24. TANG Baofu, WANG Junhai. The structural design of the sparse antenna array[J]. Electro-Mechanical Engineering, 2004, 20(4): 22-24.

[5] TAN K C, GOH S S, TAN E C. A study of the rank ambiguity issues indirection-of-arrival estimation[J]. IEEE Transactions Signal Processing, 1996, 44(4): 880-887.

[6] 吕泽均. 均匀圆阵的测向模糊研究[J]. 电讯技术, 2008, 48(7): 24 - 28. LÜ Zejun. Study on the direction finding ambiguities performance of planar antenna array based on differential geometry[J]. Telecommunication Engineering, 2008, 48(7): 24-28.

[7] SCHMIDT R O. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276-280.

[8] CARINE E K, PICHERAL J, MOKBEL C. Advantages of nonuniform arrays using root-MUSIC[J]. Signal Processing, 2010, 90(7): 689-695.

[9] CARINE E K, PICHERAL J, MOKBEL C. EM-esprit algorithm for direction finding with nonuniform arrays[C]// IEEE/SP 14th Workshop on Statistical Signal Processing. Madison WI, USA: IEEE Press, 2007: 453-457.

[10] 王文益, 彭敏英, 吴仁彪. 利用联合互质阵列的卫星导航抗干扰算法[J]. 信号处理, 2015, 31(9): 1082-1086. WANG Wenyi, PENG Minying, WU Renbiao. Interference suppression by utilizing coprime array for GNSS[J]. Journal of Signal Processing, 2015, 31(9): 1082-1086.

谈文韬 男, 1991年生, 硕士研究生。 研究方向为雷达信号与信息处理理论与技术。

林 明 男，1960年生，学士，研究员。研究方向为雷达信号与信息处理。

黎仁刚 男，1978年生，博士，研究员。研究方向为阵列信号处理。

A Study on the Direction-finding Performance of Uniform Circular Array with Odd and Even Numbered Sensors

TAN Wentao1，LIN Ming1，LI Rengang2

(1. Institute of Electronic & Information, Jiangsu University of Science & Technology, Zhenjiang 212003, China)(2. No.723 Research Institute of CSIC, Yangzhou 225101, China)

Compared with the other shapes of antenna array, uniform circular array is more suitable for the application requirements of direction-finding receiver used for electronic reconnaissance. In this paper, uniform circular array is projected into non-uniform linear array which changes with the incident angle. The characteristics of wave path difference in uniform circular array with odd and even numbered sensors are analyzed, the corresponding radius selection formulas are given, and a method for representing the error trends of direction-finding with the coefficient of correlation is proposed. Equivalences in all directions, accuracy of direction-finding, characteristics of phase ambiguity and sensitivity of array element location are simulated in two different cases. Validity of the inferences and the formulas is verified through simulation. The conclusion of this paper has high referential value for shaping a uniform circular array in engineering applications.

uniform circular array; direction-finding; odd and even numbered sensors; multiple signal classification algorithm

10.16592/ j.cnki.1004-7859.2016.11.006

谈文韬 Email：DorusTan@163.com

2016-08-19

2016-10-21

TN971

A

1004-7859(2016)11-0024-06