函数题型须注意典型错误要力避
安徽省宿州市埇桥区祁县中学(234115)
张 刚●
函数题型须注意典型错误要力避
安徽省宿州市埇桥区祁县中学(234115)
张 刚●
函数是高中数学中的最重要的内容之一,也是高考考查的重点内容之一.由于在高考中知识点多、覆盖面广、考查灵活,学生在各类考试中,由于各种原因往往会出现各种不该出现的错误,造成小题大错,失分实属可惜.本文通过对学生在学习中,由于基本概念、性质、原理等掌握不牢,而出现的各种典型错误进行剖析根源,理解和掌握函数的各种常考题型.帮助学生真正理解数学概念,弄清实质,以不变应万变,从而达到提高学生分析问题和解决问题的能力.
函数;典型错误;剖析
函数是高中数学中最重要的高考内容之一,而函数题型高考考点多、覆盖面广、考查题型灵活多变,在考试中由于各种原因常常会导致错误的发生.下面针对学生在解题过程中经常出现的典型错误进行剖析,希望能够引起学生的高度注意,从而提高学生分析问题和解决问题的能力.
一、判断函数奇偶性时,忽视定义域致错
∵f(-x)=-2x=-f(x),
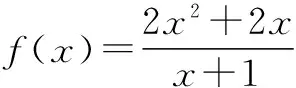
剖析 上面解题过程出错的原因是没有考虑函数的定义域,避免出现此类错误的方法是判断函数的奇偶性要遵循定义域优先的原则.
正解 ∵函数f(x)的定义域为{x|x≠-1},不关于原点对称,
∴f(x)既不是奇函数,也不是偶函数.
例2 已知函数f(x)=x2-2ax+b是定义在区间[-2b,3b-1]上的偶函数,求函数f(x)的值域.
错解 ∵f(x)是偶函数,∴f(-x)=f(x),即a=0.
∴f(x)=x2+b,从而得到函数的值域为[b,4b2+b]或[b,(3b-1)2+b].
剖析 忽视了函数的定义域关于原点对称这一条件,即-2b+3b+1=0.
正解 ∵f(x)是偶函数,∴f(-x)=f(x), 即-2b+3b-1=0.
又定义域为[-2b,3b-1],∴-2b+3b-1=0, ∴b=1.
∴f(x)=x2+1,x∈[-2,2],∴函数f(x)的值域为[1,5].
点评 判断函数的奇偶性时,首先求出函数的定义域,若定义域关于原点对称,再利用定义判断,若定义域不关于原点对称,则函数为非奇非偶函数,同时还应注意:定义域关于原点对称,且f(x)=0的函数既是奇函数,又是偶函数.
二、求函数解析式时,忽视x=0的情况或漏解致错
例3 已知f(x)为R上的奇函数,当x>0时,f(x)=x+1, 求f(x)的解析式.
错解 设x<0,则-x>0,∴f(-x)=-x+1.
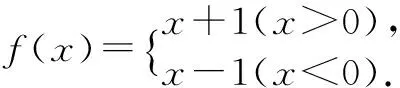
剖析 因为f(x)的定义域为R,上面错解所求得的解析式中无x=0的情况,故需补充f(0)的值.
正解 设x<0, 则-x>0,∴f(-x)=-x+1.
∵f(x)是奇函数,∴f(-x)=-f(x),∴f(x)=x-1.
当x=0时,由奇函数的定义知f(0)=0.
点评 若f(x)是R上的奇函数,则一定有f(0)=0.本题中,求分段函数的解析式时,一定要注意各“段”上定义域的并集为R,不要漏掉x=0 的情况.
三、求函数解析式时,忽略定义域致错
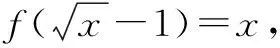
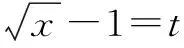
剖析 在求解函数解析式时忽略了函数的定义域导致错误,
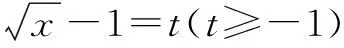
点评 用换元法求函数解析式时,要注意用于代换的新元与原定义域的变化.
四、因不能区分自变量而导致定义域错
例5 函数f(x)的定义域为[0,4],求函数f(x2)的定义域.
错解 ∵f(x)的定义域是[0,4],∴f(x2)的定义域是[0,16].
剖析f(x2)是由两个函数复合而成的,外函数是y=f(u),内函数是u=x2,而u的取值不能超出f(x)定义域,即0≤u≤4.
正解f(x)的定义域为[0,4],∴0≤x2≤4,∴-2≤x≤2.
∴f(x2)的定义域是[-2,2].
点评 函数的定义域就是自变量x的取值范围,要抓住这一关键点求解.本题中f(x)中的x满足0≤x≤4,因而f(x2)中的x2满足:0≤x2≤4, 并由其求出x的范围,即f(x2)的定义域.
五、求函数定义域时,非等价化简解析式致错
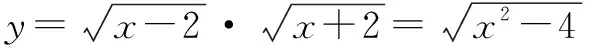
∴函数的定义域为{x|x≥2或x≤-2}.
剖析 错解在求函数的定义域时,对函数的解析式进行了不等价变形,导致定义域范围扩大。所以求函数的定义域时,一定要根据最原始的解析式来求解.
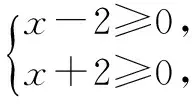
六、求二次函数最值时,忽视对称轴与区间的关系导致错误
例7 求函数y=x2-2ax+1在[0,+∞)上的最小值.
错解y=(x-a)2+1-a2≥1-a2,∴ymin=1-a2.
剖析 当x=a时,得ymin=1-a2,而对a是否在[0,+∞)内没有讨论.
正解 当a≥0时,ymin=1-a2;当a<0时,ymin=1.
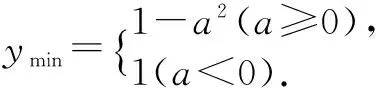
点评 有关二次函数的区间最值问题,一定要考查对称轴与区间的位置关系.
七、对“单调区间”与“在区间上单调”两个概念理解错误而出错
例8 若函数f(x)=x2+2(a-1)x+2的单调减区间是(-∞,4],则函数a的取值是____.
错解 函数图象的对称轴为直线x=1-a,由于函数在区间(-∞,4]上减函数,因此1-a≥4,即a≤-3,∴a≤-3.
剖析 错解中把单调区间误认为是在区间上单调.函数f(x)=x2+2(a-1)x+2在区间(-∞,4]上是减函数,意味着区间(-∞,4]可能是函数f(x)=x2+2(a-1)x+2的单调减区间的子集,显然与题意不符合.
正解 函数图象的对称轴为直线x=1-a,对称轴左边区间为函数的单调减区间,右边区间为函数的单调增区间. 故由函数的单调减区间为(-∞,4],可得对称轴为直线x=4,所以有1-a=4, 得a=-3.
答案:-3
点评 本题中强调的是f(x)的单调减区间为(-∞,4],而不是函数f(x)在(-∞,4]上是递减的,要注意它们的本质区别.
八、对二次函数的性质模糊而出错
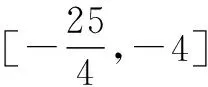
错解 D.
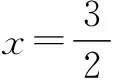
九、忽视二次项系数的取值范围致错
例10 已知二次函数f(x)=ax2+2a2+1在[2,+∞)上是递增的,求实数a的取值范围.
错解 ∵函数f(x)图象的对称轴为直线x=-a,且f(x)在[2,+∞)上是递增的,∴-a≤2,∴a≥-2.
剖析 忽视了抛物线的开口方向以及二次项系数a≠0.
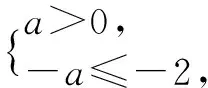
点评 解决求参数范围的问题,要借助二次函数图象,对二次项系数的符号、对称轴的位置给出限制条件,从而列出关于参数的不等式(组)求解,要注意对隐含条件的挖掘.
十、解决抽象函数问题时,忽视定义域致错
例11已知f(x)是定义在[-1,1]上的增函数,且f(x-1) 错解 ∵f(x)是增函数,且有f(x-1) 剖析 只应用了函数的单调性而忽略了函数的定义域导致错误. 正解 由题意可得 点评 在高考中对函数定义域有时直接考查,有时隐含在综合题中,这就要求考生时刻绷紧这根弦,以免掉入定义域的陷阱,因小失大. 例12 已知函数f(x)是偶函数,而且在(0,+∞)上是增函数,判断f(x)在(-∞,0)上是增函数还是减函数,并证明你的判断. 错解f(x)在(-∞,0)上是增函数.证明如下: 任取x1,x2∈(0,+∞), 且x1 ∵f(x)在(0,+∞)上是减函数,∴f(x1)>f(x2). 又∵f(x)是偶函数, ∴f(-x1)=f(x1),f(-x2)=f(x2), ∴f(-x1)>f(-x2). 又∵0>-x1>-x2,∴f(x)在(-∞,0)是增函数. 剖析 此证法是利用了区间(-∞,0)上的两个特殊值-x1,-x2来判定函数的单调性,不具有任意性.因为x1,x2虽然是(0,+∞)上的任意两个值,一但取定就是两个固定的数,所以-x1,-x2就是(-∞,0)上的两个具体数,利用区间内的两个具体数判定函数的单调性当然是错误的.所以在证明函数的单调性时一定要在待证区间上取任意两个自变量,然后比较出两个函数值的大小,进而确定出增减性. 正解f(x)在(-∞,0)上是增函数.证明如下: 任取x1,x2∈(-∞,0), 且x1 ∵f(x)在(0,+∞)上是减函数, ∴f(-x1) 又∵f(x)是偶函数, ∴f(-x1)=f(x1),f(-x2)=f(x2), ∴①式即为f(x1) G632 B 1008-0333(2016)22-0034-02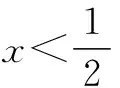
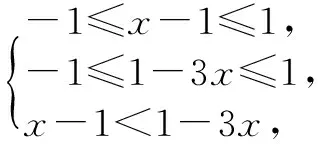
十一、利用函数奇偶性证明单调性时,忽视自变量的任意性致错

