含有函数符号“f(x)”有关问题解法浅谈

甘肃省积石山县积石中学(731700)

韩义成●



含有函数符号“f(x)”有关问题解法浅谈

甘肃省积石山县积石中学(731700)

韩义成●

函数概念比较抽象，学生对解有关函数记号f(x)的问题感到困难.学好这部分知识，能加深学生对函数概念的理解，更好地掌握函数的性质，同时培养学生灵活性，提高解题能力，对优化学生数学思维素质具有重要意义.现将常见解法及意义谈以下看法.

一、求表达式

1.换元法

即用中间变量u表示原自变量x的代数式，从而求出f(x)，这也是证某些公式或等式常用的方法，此解法培养学生的灵活性及变形能力.

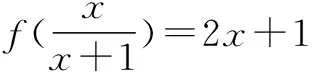
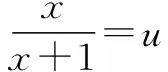
2.凑合法

在已知f(g(x))=h(x)的条件下，把h(x)并凑成以g(x)表示的代数式，再利用代换即可求f(x).此解法简洁，还能进一步复习代换法.

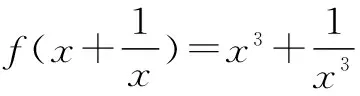
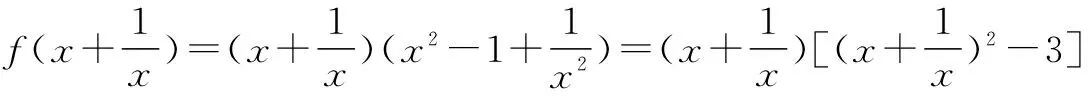
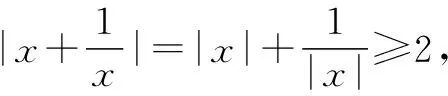
∴f(x)=x(x2-3)=x3-3x(|x|≥2).

3.待定系数法

先确定函数类型，设定函数关系式，再由已知条件，定出关系式中的未知系数.

例3 已知f(x)是二次函数，且f(x+1)+f(x-1)=x2+2x+4,求f(x).

解 设f(x)=ax2+bx+c，则f(x+1)+f(x-1)=a(x+1)2+b(x+1)+c+a(x-1)2+b(x-1)+c=2ax2+2bx+2(a+c)=x2+2x+4.

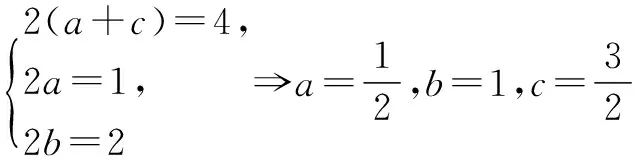
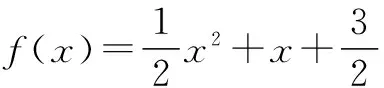
4.利用函数性质法

主要利用函数的奇偶性,求分段函数的解析式.

例4 已知y=f(x)为奇函数,当x>0时,f(x)=lg(x+1),求f(x).

解 ∵f(x)为奇函数，∴f(x)的定义域关于原点对称，故应求x<0时的表达式.

∵-x>0, ∴f(-x)=lg(-x+1)=lg(1-x).

∵f(x)为奇函数，

∴lg(1-x)=f(-x)=-f(x), ∴当x<0时f(x)=-lg(1-x).

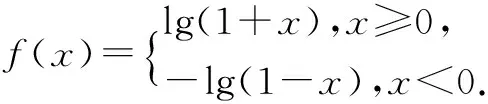
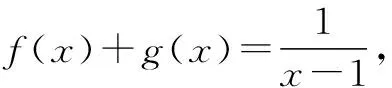
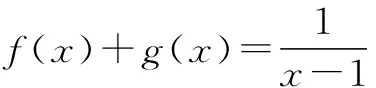
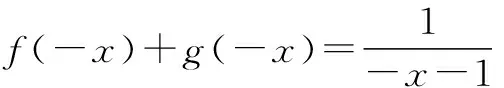
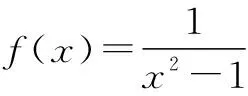
5.赋值法

给自变量取特殊值，从而发现规律，求出f(x)的表达式

例6 设f(x)的定义域为自然数集，且满足条件f(x+1)=f(x)+f(y)+xy,及f(1)=1,求f(x).

解 ∵f(x)的定义域为N，取y=1,则有f(x+1)=f(x)+x+1.

又f(1)=1,f(2)=f(1)+2,f(3)=f(2)+3，…，f(n)=f(n-1)+n，

以上各式相加，有

▶

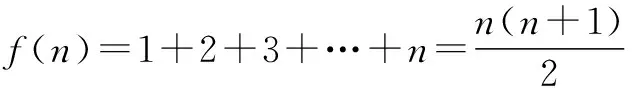
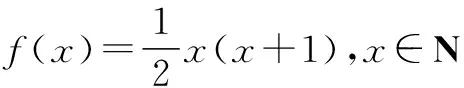
二、利用函数性质，解f(x)的有关问题

1.判断函数的奇偶性

例7 已知f(x+y)+f(x-y)=2f(x)f(y),对一切实数x、y都成立，且f(0)≠0,求证：f(x)为偶函数.

证明 令x=0, 则已知等式变为

f(y)+f(-y)=2f(0)f(y)①.

在①中令y=0,则2f(0)=2[f(0)]2.

∵f(0)≠0, ∴f(0)=1.

∴f(y)+f(-y)=2f(y), ∴f(-y)=f(y), ∴f(x)为偶函数.

2.确定参数的取值范围

例8 奇函数f(x)在定义域(-1，1)内递减，求满足f(1-m)+f(1-m2)<0的实数m的取值范围.

解 由f(1-m)+f(1-m2)<0得f(1-m)<-f(1-m2).∵f(x)为函数，∴f(1-m)

又∵f(x)在(-1，1)内递减，

3.解不定式的有关题目

例9 如果f(x)=ax2+bx+c(a>0)对任意的实数t有f(2+t)=f(2-t),比较f(1)、f(2)、f(4)的大小.

解 对任意t有f(2+t)=f(2-t), ∴x=2为抛物线y=ax2+bx+c的对称轴.

又∵其开口向上,

∴f(2)最小，f(1)=f(3).

∵在[2，+∞)上f(x)为增函数,

∴f(3)

∴f(2)

G632

B

1008-0333(2016)22-0005-02