公共自行车调度模型研究

成先镜，王正伟，冉 杰，龙圣杰

（遵义师范学院数学与计算科学学院，贵州遵义563002）

公共自行车调度模型研究

成先镜，王正伟，冉 杰，龙圣杰

（遵义师范学院数学与计算科学学院，贵州遵义563002）

随着大气污染日趋严重，“绿色出行”理念越来越深入人心，公共自行车系统应运而生，并得到迅猛发展。但在实际运营过程中存在的调度问题，即如何解决用户“借车难、还车难”和如何使企业运营成本最小化，始终制约着公共自行车系统的长期发展。根据国内外运营经验和相关研究成果发现，合理的调度是解决这些问题的关键所在。作者在分析各种调度优化模型和策略的基础上，提出了一个多目标的调度优化模型。

公共自行车系统；调度问题；多目标调度优化模型

气候变化、生态恶化越来越影响到人类的生存与发展，碳排放成为影响全球气候变暖的首要因素。而爆发性增长的小汽车则是碳排放的主要制造者之一，它们引发了交通拥堵、空气污染、噪声污染、能源消耗加大等诸多城市问题。低碳交通，作为一种“低二氧化碳排放”的绿色交通形式，在全世界许多城市正受到越来越多的推崇，而自行车当仁不让地占据首位[1]。

然而随着城市公共自行车的发展，也出现了诸多问题。从调度上看主要是用户在使用过程中出现的还车难和借车难问题，而从运营方来看则要尽量降低自行车调度的成本。只有解决了这两方面的问题，公共自行车才能得到长足发展。在各租赁点自行车动态变化的情况下，调度系统的优劣决定了运行效率的高低，因此调度系统应有精确的预测机制，预测各租赁点自行车的变化情况，同时各租赁点间自行车的调度时间也是调度系统需要考虑的重要因素之一。

在设计公共自行车调度系统模型时，需要考虑影响调度的所有因素，得到较优的目标函数。国内外针对不同的模型提出了不同的求解方法，如：贪心策略、遗传算法、车辆调度中的蚁群算法等[2,3]。

1 相关工作

目前，国内外主要围绕公共自行车调度系统调

度成本进行研究，但侧重点有所不同。

国内研究主要以降低成本为目标，目前主要以静态研究为主，即在某一时段内租赁点自行车数量不随时间变化而变化，在静态调度的情况下对公共自行车调度系统进行改进。浙江工业大学研究了公共慢行系统调度过程中租赁点需求的动态特性及其模糊时间窗的约束，为使租赁点的满意度最大化，为目标建立了公共慢行系统调度模型，并结合滚动时域调度算法对该模型进行求解，从而获得调度计划，实现了公共自行车的动态调度[4]。杭州电子科技大学针对公共自行车交通系统的静态车辆调度问题，以运输成本最少为目标，建立了公共自行车交通系统调度模型，并用模拟退火算法和遗传算法的混合算法进行求解，使车辆调度的路程缩短了近50%[2]。北京交通大学根据租赁点的分布情况，利用双层规划模型对租赁点的布局进行规划，从而提高了调度的效率[5]。

国外主要围绕动态情况下公共自行车调度模型和算法进行研究。Chemla[6]列出了单车辆在静态情况下（一定的时间段内租赁点自行车需求量无变化）的一些变化。以实现最优的平衡为目标，使用了一个分支界定算法，其搜索策略利用了局部优化的嵌入式禁忌搜索方法。在这个方法中，最重要的因素是调度过程中租赁点的访问序列，通过基于最大流计算的辅助算法得到装/卸操作的数量，通过实验证明这种方法明显减小了搜索的范围。Raviv[7]提出了基于时间、基于调度序列和基于弧的MIP模型，以用户满意度和调度路径长度为主要目标，忽略了调度过程中自行车装/卸操作的数量，该模型在巴黎Velib的60个公共自行车租赁点进行测试，结果表明，在给定的有限时间段内基于弧索引的模型能产生最好的下界，具有一定的弹性。Benchumol[8]将平衡作为最主要的约束，以总的调度路径长度作为唯一目标，选择了针对不同目标下的近似算法进行求解。Conardo[9]考察了公共自行车系统在动态情况下（租赁点自行车需求量随着时间变化而变化）平衡的变化，使用了一个基于弧流量和针对时空网络模型的计算方法，在100个租赁点和60个时间段内对该算法进行了测试，发现误差较大。

BBSS（Bicycle Balance Share System）与传统车辆调度问题（VehicleRoutingProblem,VRP）[5,10,11]有很多联系，但又有所区别。BBSS允许调度车辆多次访问租赁点，每次访问租赁点时装/卸自行车的数量是任意的。根据BBSS的特性可认为，BBSS是一个调度车辆容量有限的具有装/卸操作的单车辆VRP[18]。

现有的模型和求解方法拥有各自的优缺点。目前，较为优化和具有实际意义的模型利用了预测的机制，通过连续时间的马尔科夫链的生成过程对租赁点在未来一个时间段内是否进行调度做出判断，根据相应的约束得到可行的调度序列。本文在此基础上提出了多目标的调度优化模型。

2 调度模型研究

公共自行车系统的调度模型构建主要是围绕降低成本、用户满意度和调度时间展开，目前有以下几种较为常见的模型。

2.1 围绕用户满意度的公共自行车调度模型

董红召等[4]将模糊时间窗下的顾客满意度转化为公共自行车系统中用户的满意度，建立了公共慢性系统的动态调度模型，目标函数如下：

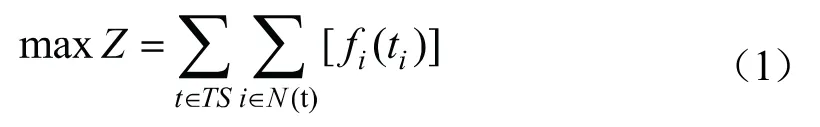
其中，

约束条件如下：

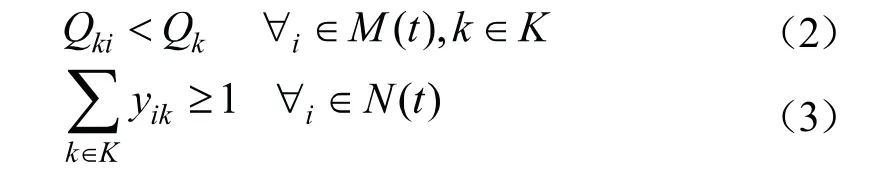
式（1）为目标函数，以总的用户满意度最大化为目标。式（2）表示在调度过程中对租赁点进行卸载的自行车数量不能超过调度车辆的最大载重量。式（3）表示任意一个有调度需求的租赁点至少有一辆调度的车辆。

2.2 围绕调度成本和调度时间的公共自行车调度模型

刘登涛等[2]主要针对静态情况下的公共自行车调度进行研究，以运输成本最小化为目标建立调度模型。在调度模型中，各个租赁点之间的距离和需求量都是已知的。

模型参数如下：

由式（4）可知调度模型的目标函数包括调度车辆的固定成本和行驶成本，运营成本为这两部分成本之和。式（5）表示调度车辆最大数目为m。式（6）表示调度车辆必须返回调度中心。式（7）表示调度车辆对租赁点只服务一次。式（8）表示每次租赁点进行调度时运出的公共自行车数量不能超过调度车辆的最大载重量。

2.3 复合模型

在公共自行车调度过程中，租赁点的需求量和实际调度后的数量、租赁点装/卸公共自行车数量和调度时间是衡量调度效率的重要指标。Marian[12]针对这三个方面建立了较为复杂的调度模型。此模型在调度的过程中，主要关注两部分：按序访问租赁点的路径和租赁点进行装/卸的自行车数量。

模型参数如下：

调度平衡后的自行车数：

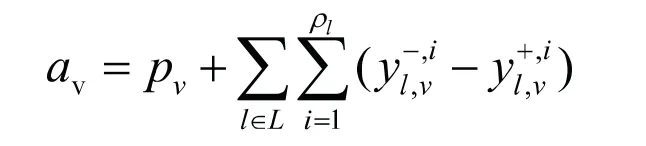
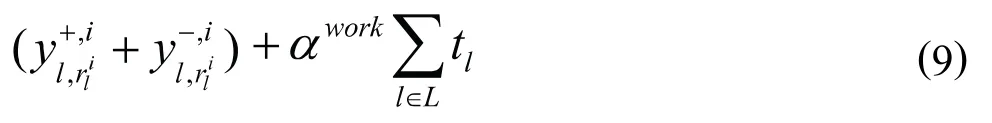
以上三类调度模型各有优缺点。围绕用户满意度模型忽略了调度成本和调度时间，单纯地追求用

户满意度最大化。围绕调度成本和调度时间模型追求调度成本和调度时间的最小化，忽略了用户满意度。复合模型将用户满意程度转化为将调度成本转化为计算租赁点装/卸自行车的数量和调度时间，考虑得比较全面，而在实际调度中，发现偏差的值很难得到，因此，需要将此模型进行转化，可通过精确的预测机制求得偏差建立一个新的、易求解的调度模型，也即多目标调度优化模型。

3 多目标调度优化模型

公共自行车调度的目的是为了解决用户借车难和还车难的问题，旨在满足用户满意度的前提下，使调度成本最低。影响调度效率的三个因素为用户满意度、调度成本和弹性时间窗。用户满意度的计算，需要采用预测机制，利用以往租赁点的历史数据，预测出在未来一个时间段内租赁点自行车的需求量。调度的过程是动态的，租赁点自行车的需求量随着时间的变化而变化，此时，将调度时间分为一系列小的时间段。这种时间连续、租赁点状态离散的特点符合连续时间的马尔科夫链的生成过程，结合用户无法租车和无法还车的惩罚值可得到用户满意度；调度的成本与距离密切相关，在计算时通过时间来表示，包括调度车辆根据调度路线在各租赁点间行驶所花费的时间、调度车辆在租赁点停靠的时间、租赁点装/卸自行车所花费的时间和调度车辆在路口等红绿灯的时间；调度车辆到达租赁点所需的时间也是公共自行车调度系统的影响因素之一，而租赁点对于调度车辆到达的时间应该具有一定弹性，本文定义为时间满意度。

模型系数如下：

两阶段调度策略下调度模型的目标函数为：

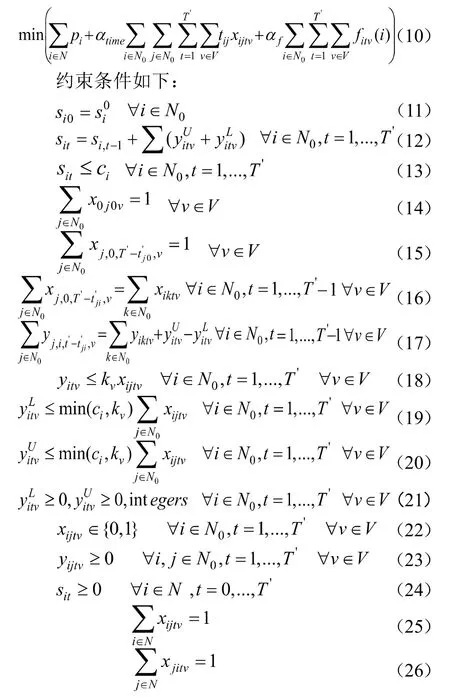
式（10）为本文中两阶段调度策略下调度模型的目标函数，由以下三部分组成：

（1）租赁点无法还车和无法借车的惩罚值之和的计算。当租赁点无车可借时，对用户无法借车设置惩罚值并计算，同理，计算租赁点自行车已满时用户无法还车的惩罚值。

（2）调度车辆的调度时间。

（3）租赁点的时间满意度。利用车辆调度中计算模糊时间窗下顾客满意度的方法，得到公共自行车系统中租赁点对调度车辆到达时间的满意度。

式（11）表示租赁点i初始时刻的可借自行车数。式（12）表示租赁点i的容量平衡即t时刻租赁点i的可借自行车数为t-1时刻租赁点i的可借自行车数加上调度车辆v对租赁点i调度的装/卸自行车数。式（13）表示t时刻租赁点i的可借自行车数不能超过租赁点i的容量。式（14）表示开始时刻调度车辆v离开调度中心。式（15）表示结束时刻调度车辆回到调度中心。式（16）表示车辆流量守恒公式，确保调度车辆的调入和调出时的自行车数平衡。式（17）表示调度车辆v的自行车数守恒公式。式（18）表示t时刻从租赁点i到j装载的自行车数不能超过调度车辆v的最大载重量。式（19）表示调度车辆v在租赁点i需要的装载量为租赁点i容量和调度车辆最大载重量的最小值。式（20）表示调度车辆v在租赁点i需要的卸载量为租赁点i容量和调度车辆v最大载重量的最小值。式（20）～（24）为相应变量的完整性和非负的线性约束。式（25）和式（26）表示在t时刻调度车辆对租赁点i和j只调度一次。

3.1 租赁点惩罚值的计算

在多约束条件下，调度过程中最重要的一点是在未来时间段租赁点所期待的自行车数，即需要对租赁点是否进行调度做出预测。根据预测出来的结果得到租赁点序列，进行调度。在公共自行车调度的过程中，调度时间是连续的，各租赁点所期待的自行车数会随着时间的变化而变化。在某一时间段内，租赁点的状态是离散的即需要装载、卸载和不变动。这种时间连续、状态离散的特点符合连续时间马尔科夫链的生成过程的特性。鉴于此，本文用马尔科夫链的生成过程对租赁点做出预测。

生灭过程[13,14]的变化情况分为三种情形：

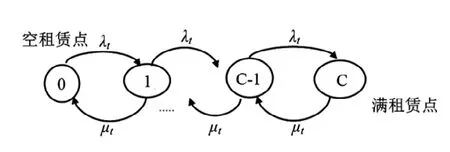
图1 表示租赁点变化的连续时间的马尔科夫链

相关参数如下：

p：租赁点可借自行车数为零时用户无法借车的惩罚值

h：租赁点空车位数为零时用户无法还车的惩罚值

根据租赁点以往数据得到转移概率矩阵p，通过笛卡尔积得到从初始到t时刻的概率值

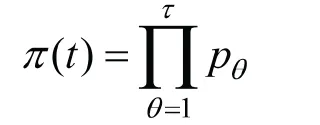
假设用户无法借车的惩罚值和无法还车的惩罚值是一样的，即p=h=1。由于租赁点状态是离散的。所以，得到的目标是用户在租赁点无法借车和还车惩罚值之和，即

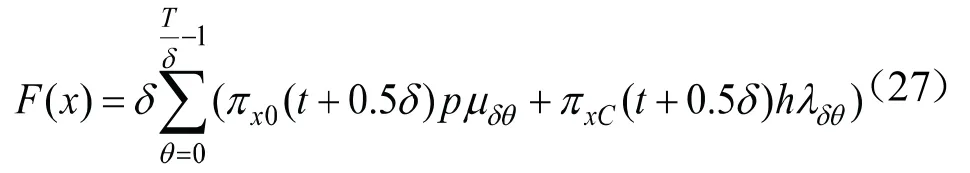
由式（27）得到租赁点的惩罚值之和，对应于式（10）中的p，得到调度的租赁点序列。这种求解方式利用了预测的机制，租赁点生成率和死亡率的值越精确，求得的预测情况就越符合实际情况。

3.2 调度时间

在公共自行车调度过程中，调度时间主要分为以下几个部分：

（1）调度车辆的行驶时间。行驶的路程越长，所耗费的时间越长，成本越高，反之，成本越低。

（2）调度车辆在所经路段等红绿灯的时间。

（3）调度车辆在各租赁点的停车时间，主要为装/卸自行车的时间、停车和起步的时间。

3.3 时间满意度

在公共自行车调度系统中，调度车辆到达租赁点是有时间要求的。本文引入物流系统满意优化理论[15]。满意优化理论的关键是建立一个反映变量取值（客观）与客户心理反应（主观）之间关系的数学表达式，也就是客户满意度和客户满意度函数[16]。传统的车辆调度系统用硬性的时间窗作为对调度车辆的时间约束，而在实际调度时，硬性的时间窗不能反映顾客的满意度，顾客可能倾向于在某个特定的时间段内接受服务，也可能在其他时间段内接受服务，在不同的时间段内顾客接受服务会有不同的满意度。

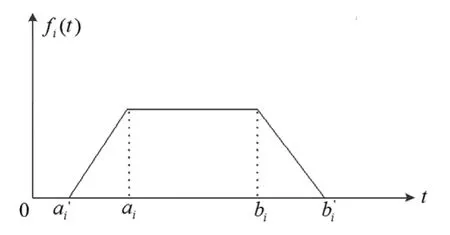
图2 顾客i的满意度

在图2中，a为顾客满意的最早服务时间，b为顾客满意的最晚服务时间，a2为顾客可接受的最早服务时间，bi为顾客可接受的最晚服务时间为顾客满意的服务区间，为顾客可接受的服务区间，其顾客满意度公式fi(t)的定义如下：

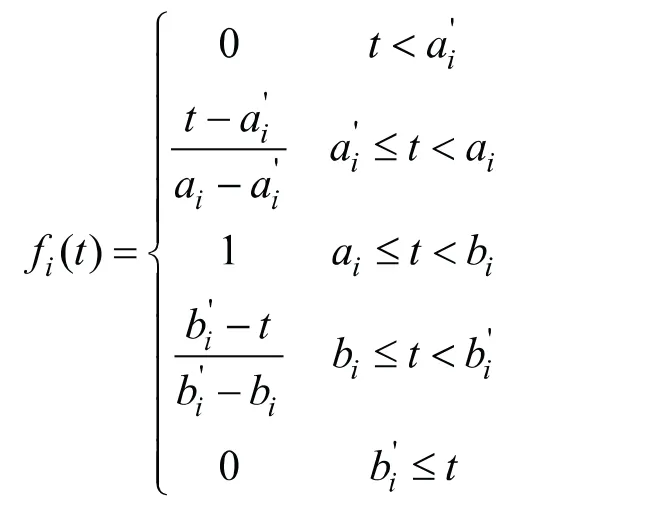
在本文的公共自行车调度系统中，对到达租赁点的调度车辆有时间限制（即软时间窗），称为时间满意度。将顾客满意度的概率和计算方法运用到公共自行车调度系统中，由式（10）可知，模型的目标函数得到最小值。故将顾客满意度函数fi(t)作如下修改：设为租赁点i可接受调度车辆服务的开始时间为租赁点i可接受调度车辆服务的最晚到达时间，为租赁点i期望的服务时间，如图3所示。

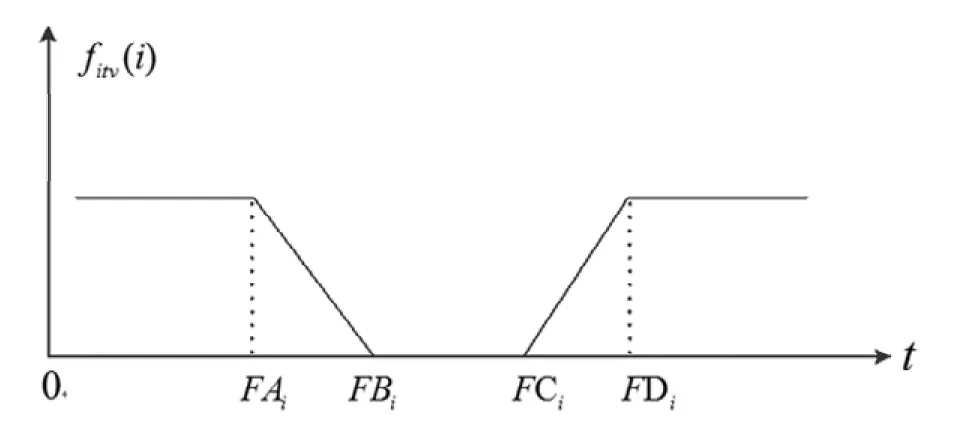
图3 模糊时间窗

随着调度车辆达到租赁点时间的不同，相应的时间满意度也会发生变化。时间满意度的定义如下：

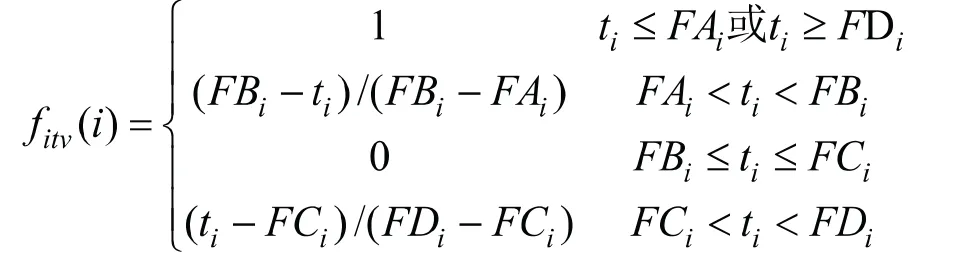
根据以上定义计算出租赁点的时间满意度，即式(10)的第三部分。

4 案例分析

选取10租赁点下对未采用两阶段调度策略、采用两阶段调度策略和基于邻域搜索算法采用两阶段调度策略进行调度。由于上述10个租赁点在不同调度条件下的租赁点惩罚值和调度时间固定不变，故记录不同租赁点个数的时间满意度、程序运行时间和目标值进行对比分析，时间系数 分别选取1,1/5,1/10,1/15。

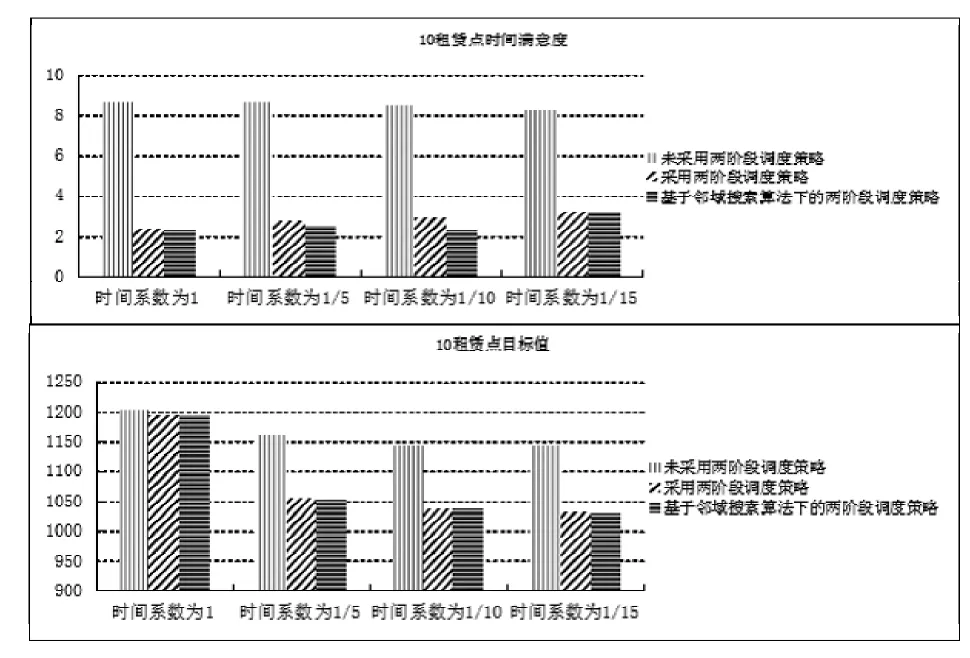
图4 租赁点为10个时的数据分析

在对10个租赁点进行调度时，采用两阶段调度策略的时间满意度低即用户满意度高，基于邻域搜索算法的两阶段调度策略的时间满意度要略低于两阶段的时间满意度，即基于邻域搜索算法的两阶段调度策略的用户满意度最高。此外，其目标值也低于两阶段调度策略下的目标值。

由表1可知，不同时间系数值的程序运行时间差距较大，其中未采用两阶段调度策略的运行时间最长，采用两阶段调度策略运行时间显著少于未采用两阶段调度策略的运行时间，而采用基于邻域搜索算法的两阶段调度策略的运行时间最少。

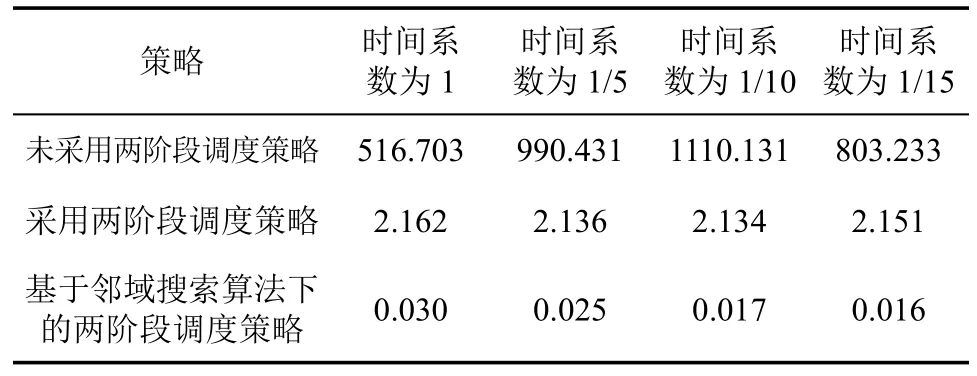
表1 租赁点为10个时的程序运行时间（s）

5 总结

本文针对公共自行车调度系统存在的问题，对当前的调度模型进行了分析和总结。主要关注了公共自行车系统的动态调度过程模型，针对各调度模型存在的优缺点，结合预测机制、调度时间和用户满意度，提出了多目标的调度优化模型。而在动态调度过程中还存在很多复杂的问题，如用户出行规律、早晚高峰期自行车数量、精确的预测机制、调度模型是否合理等，还有待进一步的研究。

[1]龚迪嘉,朱忠东.城市公共自行车交通系统实施机制[J].城市交通,2008,6(6):27-32.

[2]刘登涛,方文道,章坚民,等.公共自行车交通系统调度算法[J].计算机系统应用.2011,20(9):112-115.

[3]张建勇，郭耀煌，李军.基于顾客满意度的多目标模糊车辆优化调度问题研究[J].铁道学报,2003,25(2):15-17.

[4]董红召,赵敬洋,郭海锋,等.公共慢行系统的动态调度建模与滚动时域调度算法研究[J].公路工程,2009,34(6):68-75.

[5]李婷婷.城市公共自行车租赁点选址规划研究[D].北京:北京交通大学,2010.

[6]Chemla D,Meunier F,Calvo R W.Bike sharing systems:Solving the static rebalancing problem[J].Discrete Optimization, 2013,10(2):120-146.

[7]Raviv T,Tzur M,Forma I A.Static Repositioning in a Bike-Sharing System:Models and Solution Approaches[J].EURO J Transp Logist,2013,(2):187-229.

[8]Benchimol M,Benchimol P,Chappert B,et al.Balancing the stations of a self-service bike hire system[J].RAIRO Operations Research,2011,45(1):37-61.

[9]Contardo C,Morency C,Rousseau L M.Balancing a Dynamic Public Bike-Sharing System[R].Transportation Science,2012.

[10]贺竹磬,孙林岩.动态交通下车辆路径选择模型及算法[J].交通运输工程学院学报,2007,7(1):112-115.

[11]史彩霞.基于公共自行车调度系统的运行分析和研究[D].杭州：浙江工业大学,2013.

[12]Marian R H,Petrina P,Hu B.Balancing Bicycle Sharing Systems:A Variable Neighborhood Search Approach[R]. EvoCOP 2013,LNCS 7832,Springer-Verlag Berlin Heidelberg,2013.121-132.

[13]王梓坤,杨向群.生灭过程与马尔可夫链[M].北京:科学出版社,2005.

[14]Raviv T,Kolka O.Optimal inventory management of a bikesharing station[J].IIE Transactions,2013,1(45):1077-1093.

[15]张建勇,郭耀煌,李军.基于顾客满意度的多目标模糊车辆优化调度问题研究[J].铁道学报,2003,25(2):15-17.

[16]Bent R,Pascal V H.A Two-Stage Hybrid Local Search for the Vehicle Routing Problem With Time Windows[J].Transportation Science,2004,38(4):515-530.

（责任编辑：朱 彬）

On the Dispatching Mode of Bicycle

CHENG Xian-jing，WANG Zheng-wei，RAN Jie，LONG Sheng-jie
(School of Maths and computational Science,Zunyi Normal College,Zunyi 563002,China)

As air pollution is increasingly serious,the concept of“Green Travelling”goes deep into the people’s mind;and the bicycle system arises at this very moment,and gains rapid development.However,there exists dispatching problem in the actual performance, viz.,how to tackle the customer’s problem of borrowing bicycle and returning it and how to minimize the operation cost of business, and these two factors restrict development of bicycle system in the long run.The operative experience from home and abroad as well as the relevant findings shows that proper dispatching system is the key to solving these problems.After analyzing the various optimum dispatching models and strategies,the author of this paper propounds an optimum dispatching model with multiple purposes.

bicycle system;dispatching problem;optimum dispatching model with multiple purposes

TP399

A

1009-3583（2016）-0094-07

2016-03-12

成先镜，男，贵州遵义人，遵义师范学院数学与计算科学学院教师，硕士。研究方向：智能交通。