活塞声源膜板在弹性边界条件下的线谱分析

吴垣甫， 王久法， 高 频

(1. 重庆大学 自动化学院，重庆 400044; 2. 中国船舶重工集团公司第七一○研究所，宜昌 443003)



活塞声源膜板在弹性边界条件下的线谱分析

吴垣甫1， 王久法2， 高 频2

(1. 重庆大学 自动化学院，重庆 400044; 2. 中国船舶重工集团公司第七一○研究所，宜昌 443003)

平行四边形活塞声源模拟舰船声场线谱特征时，为了实现其具有较高的效率，应保证声源膜板结构的固有频率与线谱频率相等，因此，分析膜板结构的振动特性具有重要意义。采用改进Fourier级数的方法建立平行四边形膜板结构的振动模型，通过在膜板结构的四边上布置弹簧来模拟任意弹性边界条件，结构的振动位移函数表示为标准的二维Fourier余弦级数和辅助级数的线性组合。通过辅助级数的引入，解决了位移函数的导数在边界潜在的不连续的问题，从而使此法适用于任意的弹性边界条件。结合Hamilton原理，推导出平行四边形板结构振动方程的矩阵表达示，板结构的振动参数可通过求解矩阵值得到。最后进行了数值仿真，求解出结构在不同参数下的线谱频率，并与文献以及有限元结果进行对比，验证了该方法的精确性。

平行四边形板；改进的傅里叶级数；弹性边界条件；Hamilton原理

活塞声源作为一种重要的声源模拟结构， 广泛应用于军事领域以及工程领域中。 如在反水雷、反潜作战中，活塞声源常用于模拟舰船和潜艇的声场。舰船和潜艇的声场是由机械噪声、螺旋桨噪声和水动力噪声组成，其在低频区具有多个线谱。由于线谱比连续谱的谱级高，因此，活塞声源在模拟线谱时需要具有更高的效率，即活塞声源膜板结构工作在固有频率处。为了充分发挥活塞声源的功能，研究活塞声源膜板结构的振动特性具有重要的意义。

目前，活塞声源膜板常见的结构有圆形板以及矩形板。由于平行四边形独特的结构，通过改变两边的夹角可以灵活控制结构的振动特性，近年来，平行四边形板也开始应用于活塞声源中。为了提高平行四边形活塞声源在模拟舰船声场线谱的效率和准确度，平行四边形板结构的振动特性研究成为了迫切需要解决的问题。虽然，许多学者对板结构的振动特性进行了大量的研究，并取得了丰硕的成果。不过，这些成果主要针对矩形板结构，平行四边形板结构由于振动方程的复杂性，其振动特性的研究还不深入。

为了研究平行四边形板结构的振动特性，需要建立振动控制方程和边界约束方程，以及对振动控制方程和边界条件所构成边值问题的求解。目前，建立振动控制方程的理论主要有Kirchhoff理论、Mindlin理论、Ressner 理论以及三维理论等，与Kirchhoff理论相比，后三种理论可以建立更精确的方程。不过，工程中常见的平行四边行板结构大多为薄板结构，其厚宽比远远小于1，Kirchhoff理论的精度也将满足要求，因此，大多学者均采用Kirchhoff理论。

对于振动方程的求解，主要有Rayleigh-Ritz法、叠加法、有限元法以及微分求积法等。如MIZUSAWA等[1-2]采用Rayleigh-Ritz法研究了平行四边形板在不同边界条件下的振动、屈曲和弯曲解问题。GORMAN[3]在直角坐标系下采用单Fourier级数叠加法得到了平行四边形板结构自由振动解。MCGEE等[4]用四边形等参单元，分析了悬臂边界条件下的平行四边形板的振动特性。WOO等[5]使用P型有限元法分析了四边形板的自由振动特性。王克林等[6-7]采用叠加法对简支平行四边形板结构在面内张力和剪力作用下自由振动、屈曲和弯曲问题作了全面的研究，在此基础上，分析了有自由边的平行四边形板的自由振动解。LAI等[8-13]采用微分求积等新方法对平行四边形板的振动特性进行了研究。

不过，这些方法都有自身的缺点，如Rayleigh-Ritz法需要选取合适的挠度函数，而挠度函数和边界条件有关，其选择比较困难；叠加法需要将边界条件进行分解，需要较高的技巧性；有限元法适用于中低频段的求解；微分求积法的加权系数和样点的选择规则还不明确。

同时，这些研究在建立边界约束方程时，为了简化复杂边界条件带来的困难，将其局限为固支、简支和自由三种类型的边界条件。虽然这使问题得以简化，但也使研究结果具有了一定的局限性。从工程实际角度看，平行四边形板结构的边界条件并非仅仅局限于这几种经典边界条件，还存在着均匀弹性支撑等复杂的边界条件，建立平行四边形板在弹性支撑下的振动模型具有重要的意义。

针对目前平行四边行活塞声源膜板结构的振动研究在边界条件以及求解方法的局限性，本文基于Kirchhoff理论，采用改进Fourier级数方法分析了平行四边形板在弹性边界条件的振动特性。采用横向位移约束弹簧和旋转位移约束弹簧来模拟结构的任意弹性边界条件。结构的振动位移函数描述为标准的二维Fourier级数和四项辅助的单Fourier级数的线性组合，通过辅助级数的引入，解决位移函数在边界潜在的不连续性问题，使振动位移函数能够适用于任意的弹性边界条件。结合Hamilton原理，建立了平行四边形板的振动模型。最后给出了数值分析结果，求解了板结构的振动特性，讨论了结构参数及边界条件对活塞声源线谱频率的影响，并与文献以及有限元法的结果进行了对比，验证本方法的准确性。

1 理论模型的建立

本文所研究的平行四边形活塞声源膜板如图1所示，板长为a，宽为b，厚度为h，相邻两边的夹角为α。为了模型的通用性，板结构的边界条件通过在四个边界处分别设置横向位移约束弹簧和旋转约束弹簧两种类型的弹簧，通过改变弹簧的刚度值来对任意的边界条件进行模拟。所有的经典边界条件都能够通过将三种弹簧系数设置为无穷大或零来获得。

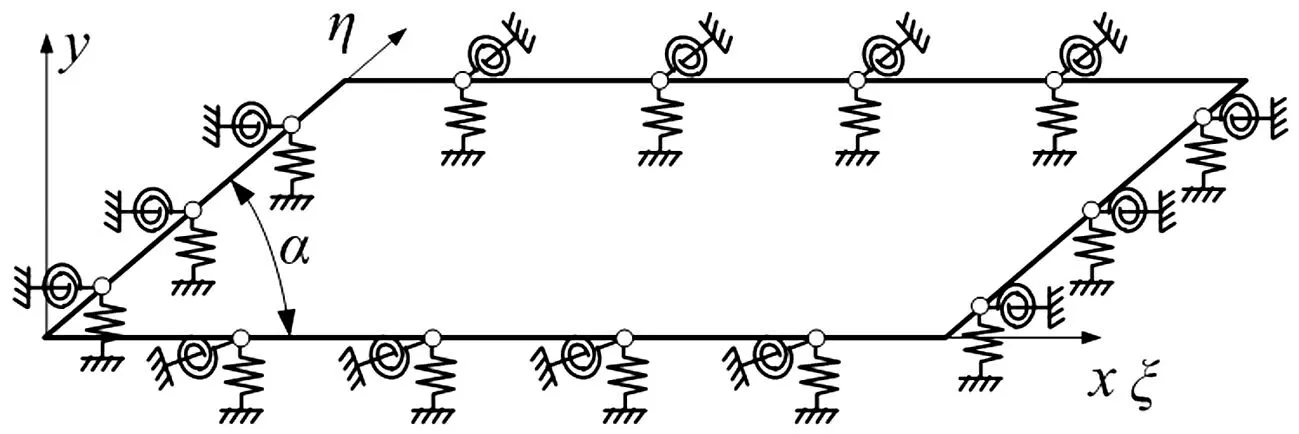
图1 任意边界条件下板结构示意图Fig.1 A plate with general elastic boundary support

例如将四边上的横向位移约束弹簧的刚度值设置为无穷大，而将四边上的旋转约束弹簧刚度值设置为零，就相当于模拟了四边简支的边界条件；将四边上的横向位移约束弹簧和旋转约束弹簧的刚度值均设置为零，就相当于模拟了四边自由的边界条件。

为了便于建立平行四边形活塞声源膜板的振动方程，取如图1所示的斜坐标系0ξη，其坐标轴分别沿着平行四边形的两边。根据几何关系，可建立斜坐标系和直角坐标系间的关系：

ξ=x-ytanβ

(1)

η=ysecβ

(2)

式中:β为斜坐标系0η轴与直角坐标系0y轴的夹角，β=π/2-α。斜坐标系中薄板的振动控制方程为

(3)

式中:w为平行四边形膜板的振动位移。直角坐标系为斜坐标系β=0时的特殊情况，当时，式(3)即为矩形板的振动控制方程。

由力学知识可得，平行四边形膜板结构的Hamilton方程为：

(4)

式中:V为平行四边形膜板结构的总势能，T为平行四边形膜板结构的总动能，Wext为外力做的功。对图1所示的板结构，总势能可写为：

V=Vplate+Vspring

(5)

式中:Vplate为膜板矩形板的势能，Vspring为模拟边界条件的弹簧势能。

式中:

(6)

(7)

(8)

(9)

如果外载荷为集中力，则外载荷的表达式为：

f(ξ,η)=Fδ(ξ-ξ0)δ(η-η0)

(10)

此时的外载荷所做功的表达式为

(11)

式中:δ为Delta函数，F为力的幅值，ξ0和y0为外力作用点的坐标值，ρ为密度，μ为泊松比，h为厚度，D=Eh3/(12(1-μ2))为弯曲刚度。

kξ0和Kξ0(kξa和Kξa) 分别为ξ=0(ξ=a)处横向位移和旋转约束弹簧刚度，kη0和Kη0(kηb和Kηb)分别为η=0(η=b)处横向位移和旋转约束弹簧刚度。

2 振动位移函数

平行四边形活塞声源膜板的位移函数可通过沿ξ和η轴方向的两个分量来描述，本文中，位移采用二维改进Fourier级数展开来表示[14-15]：

(12)

式中：λm=mπ/a，λn=nπ/b，Amn、clm、dln分别为用来描述板结构弯曲振动未知的Fourier系数和辅助级数的系数。与x相关的辅助函数分别表示为：

(13)

(14)

(15)

(16)

从式(12)可以看出，振动位移函数展开时除了标准的二维Fourier级数，还有四项辅助的单Fourier级数。在四条边界上，挠度和转角关于ξ和η的一阶偏导潜在的不连续将有效地转移到了辅助项，因此，位移函数和转角函数在整个板的求解域内展开时都有连续的一阶导数。所以这种Fourier级数解形式，不仅适用于任意边界条件，也可以改善级数的收敛性。

将式(12)～(16)代入Hamilton方程(2)中，对未知Fourier系数求极值，这样就能够得到一个线性方程组，写成矩阵表达式为

(K-ω2M)A=F

(17)

式中:A和F分别为未知的Fourier系数向量和外部载荷作用向量，其形式为

A={A0,0,A0,1,…，AM,N,c11,c12,…，

c1M,c21,c22,…，c2M,c31…，c4M,d11,d12,…，

d1N,d21,d22,…，d2N,d31…，d4N}T

(18)

F具有与A相同的向量形式，当F=0时，即可进行模态分析。M为平行四边形板结构的质量矩阵，K为刚度矩阵，其形式为：

(19)

(20)

{M11}s,t=

(21)

{M12}s,m′+1=

(22)

{M13}s,m′+1=

(23)

{M14}s,m′+1=

(24)

{M15}s,m′+1=

(25)

{M16}s,n′+1=

(26)

{M17}s,n′+1=

(27)

{M18}s,n′+1=

(28)

{M19}s,n′+1=

(29)

式 (21)～(29)给出了质量矩阵M的第一行子矩阵，M和K的其它子矩阵可以依此形式写出，式中m′=0,1,…,M，m=0,1,…,M，n′=0,1,…,N，n=0,1,…，N，s=m(N+1)+n+1,t=m′(N+1)+n′+1,M、N表示展开级数的截断值，其数值依据结果所需要达到的精度来确定。

3 数值计算

平行四边形活塞声源膜板的结构及其材料参数为：板的长度为a，宽度为b，长宽比为a/b，板的厚度h=0.005 m，板的密度ρ=2 700 kg/m3，结构阻尼因子为η=0.01，弹性模量E=70 GPa，泊松比μ=0.3。文中为了表述方便，用C表示固支边界条件，F表示自由边界条件，S表示简支边界条件。

为了验证本文方法的准确性，表1给出了平形四边形活塞声源膜板在不同夹角和不同边界条件下的前六阶无量纲线谱频率ωa2(ρh/D)1/2，同时给出了有限元法、文献[11]中微分求积法以及文献[16]中解析法求得的结果。可以发现本方法的结果和精确值的结果吻合良好，两者的误差在1%内。在本文计算过程中，两个方向的位移展开采用相同的截断数，表1中的值是M=N=12时的计算结果。

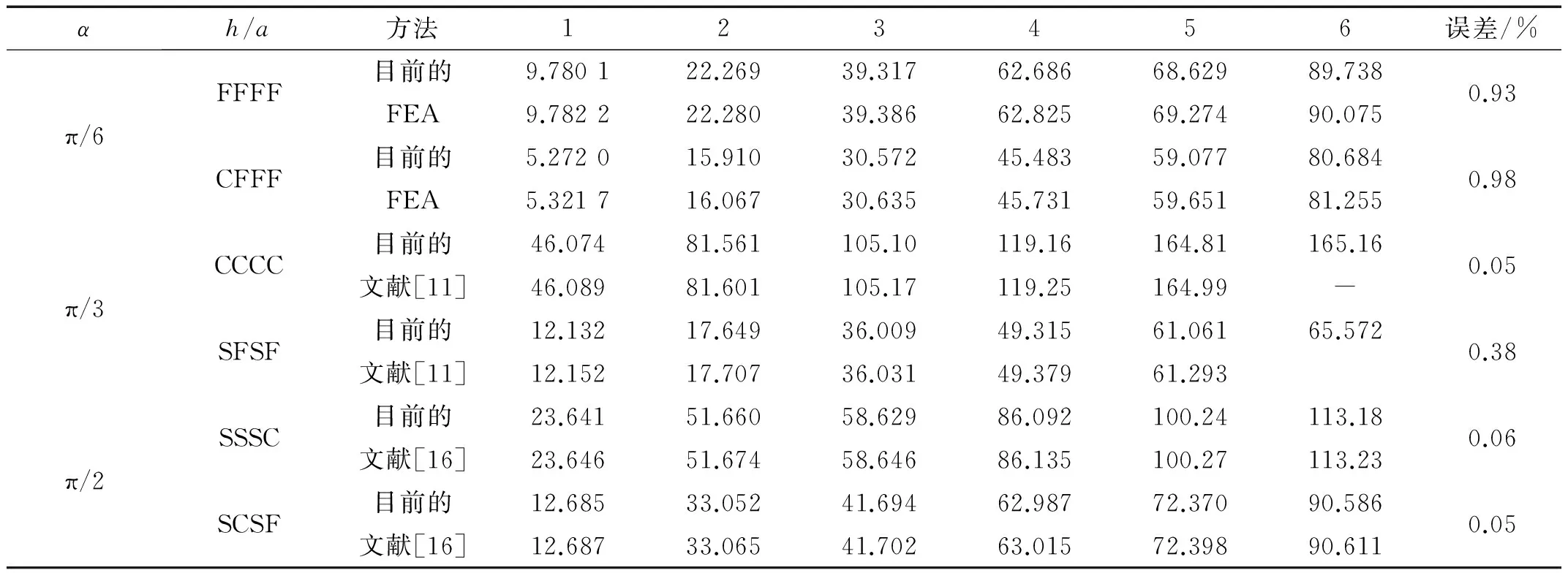
表1 平行四边形膜板的线谱频率

对于给定的线谱频率，将求解的未知系数代入振动位移方程(12)中，可以很方便地得到各点的位移。图2给出了采用本文方法得到的平形四边形膜板在SFCF边界条件下的前四阶振型，平行四边形膜板的a/b=1，两边的夹角α=π/6。为了验证本方法的准确性，图3给出了采用有限元法得到前四阶振型。通过比较，可以看出本文方法振型图与有限元法得到的结果基本相同。

图2 SFCF平行四边行膜板的前四阶振型Fig.2 The first four mode shapes for SFCF tapered plates

图3 SFCF平行四边形板的前四阶振型(ansys)Fig.3 The first four mode shapes for SFCF tapered plates with ansys

为了检验本文方法的收敛性，表2给出了平行四边形膜板在不同截断数下的前六阶线谱频率，板的边界条件为CFFS，板的a/b=1，两边的夹角α=π/6，截断数M=N为6到18。为了评价收敛精度，表中给出了相对误差ε，表示截断数取相邻的两整数时前六阶的最大相对偏差ε。ε=max{[(Ωi)Z-(Ωi)Z+1]/(Ωi)Z×100%}，其中，(Ωi)Z表示截断数M=N=Z时，变厚板的第i阶无量纲振动频率。从表中可以看出，截断数取较小值时就能得到精确的结果，而且随着截断数的增加，结果得到一致性改善，即本方法有良好的数值稳定性。在实际计算时，截断数根据相对误差选取，本文下面的算例中，截断数取为相对误差小于0.1%时的值。

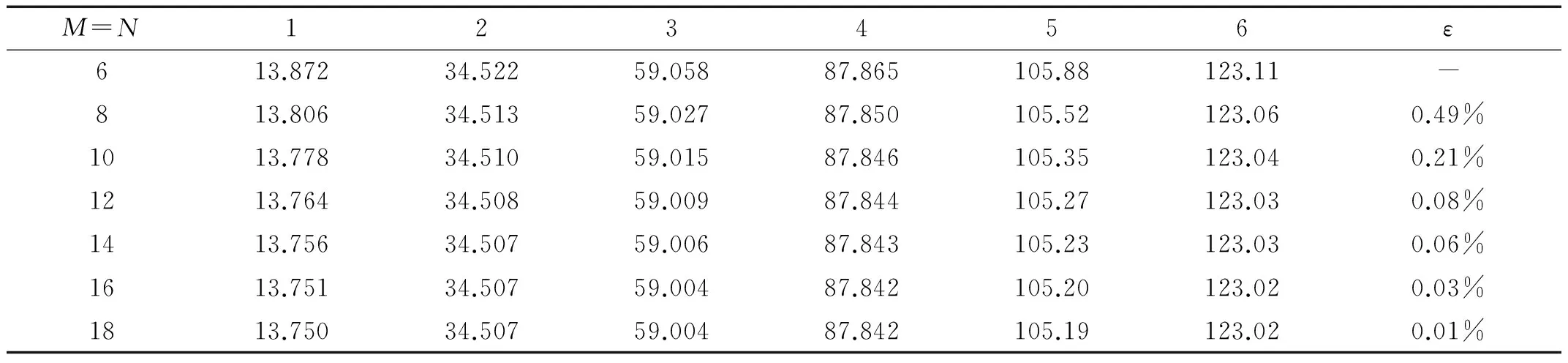
表2 不同截断数下平行四边形膜板的线谱频率

由于处理弹性边界条件在数学处理上的复杂性，传统方法大多只研究板结构在经典边界条件下的振动特性，而忽略了对弹性边界条件的研究。本方法采用约束弹簧来模拟边界条件，通过将其作为振动方程中的一个参数，使边界条件的问题转化为弹簧刚度参数设置的问题，从而便于研究边界条件对振动特性的影响。

表3给出了边界条件为CFFF的平行四边形膜板在ξ=0边上的横向位移弹簧刚度变化时的前六阶无量纲线谱频率ωa2(ρh/D)1/2，kξ0=K×D，K为弹簧刚度系数，板的a/b=1，两边的夹角α=π/4。从表3可以看出，随着横向位移弹簧刚度值的增大，板的线谱频率随之增加，弹簧刚度系数K的影响范围主要集中在D～10 000×D，当弹簧刚度系数K增加到106时，振动频率基本上趋于恒定。

4 结 论

本文采用改进Fourier级数方法建立了平行四边形活塞声源膜板的振动模型，分析了其在弹性边界条件的线谱频率。为了模型的通用性，板结构的边界条件采用横向位移约束弹簧和旋转位移约束弹簧来模拟。平行四边形活塞声源膜板的振动位移函数描述为标准的二维Fourier级数和四项辅助的单Fourier级数的线性组合，通过辅助级数的引入，解决位移函数在边界潜在的不连续性问题，使振动位移函数能够适用于任意的弹性边界条件。结合Hamilton原理，建立了平行四边形活塞声源膜板振动方程的矩阵表达式，板结构的固有频率和振型可以通过求解矩阵得到。最后进行了数值仿真，求解了平行四边形活塞声源膜板在不同夹角、不同边界条件下的线谱频率，并与文献中的结果以及有限元法的结果进行了对比，验证了本方法的准确性。通过设置截断数M和N为不同的数值，表明本方法具有很好的收敛性。

[1] MIZUSAWA T, KAJITA T, NARRUOKA M. Analysis of skew plate problems with various constraints[J]. Journal Sound and Vibration, 1980, 73(4): 575-584.

[2] SUBRAHMANYAM M B, WAH T. Vibration of quadrilateral plates[J]. Computer Methods in Applied Mechanics and Engineering, 1984, 43(3): 315-323.

[3] GORMAN D J. Accurate analytical-type solutions for the free vibration of simply-supported parallelogram plates[J]. Journal of Applied Mechanics, 1991, 58(2): 203-208.

[4] MCGEE O G, BUTALIA T S. Natural vibrations of shear deformable cantilevered skew thick plates[J]. Journal of Sound and Vibration, 1994, 176(3): 351-376.

[5] WOO K S, HONG C H, BASU P K, et al. Free vibration of skew mindlin plates by p-version of FEM[J]. Journal of Sound and Vibration, 2003, 268(4): 637-656.

[6] 王克林，刘俊卿. 有面内张力和剪力作用的简支各向异性平行四边形板自由振动、屈曲和弯曲的精确解[J]. 振动与冲击, 2006, 25(2): 93-96. WANG Kelin, LIU Junqing. Free vibration, buckling and bending analysis of anisotropic skew plates with simply edges[J]. Journal of Vibration and Shock. 2006, 25(2): 93-96.

[7] 王克林，李璐，汤翔,等. 有自由边的各向异性平行四边形板的弯曲、振动与屈曲的傅里叶分析[J]. 工程力学, 2008, 25(3): 31-37. WANG Kelin, LI Lu, TANG Xiang, et al. Free vibration, buckling and bending analysis of anisotropic skew plates with free edges using fourier series[J]. Engineering Mechanics, 2008, 25(3): 31-37.

[8] LAI S K, ZHOU L, ZHANG Y Y, et al. Application of the DSC-element method to flexural vibration of skew plates with continuous and discontinuous boundaries[J]. India Quarterly A Joural of International Affairs, 2009, 65(4):393-404.

[9] DOZIO L, CARRERA E. Ritz analysis of vibrating rectangular and skew multilayered plates based on advanced variable-kinematic models[J]. Composite Structures, 2012, 94(6): 2118-2128.

[10] EFTEKHARI S A, JAFARI A A. Simple and accurate ritz formulation for free vibration of thick rectangular and skew plates with general boundary conditions[J]. Acta Mechanica, 2013, 224(1): 193-209.

[11] EFTEKHARI S A, JAFARI A A. Modified mixed ritz-DQ formulation for free vibration of thick rectangular and skew plates with general boundary conditions[J]. Applied Mathematical Modelling, 2013, 37(12/13): 7398-7426.

[12] WANG X W, WANG Y L, YUAN Z G. Accurate vibration analysis of skew plates by the new version of the differential quadrature method[J]. Applied Mathematical Modelling, 2014, 38(3): 926-937.

[13] JIN C H, WANG X W. Weak form quadrature element method for accurate free vibration analysis of thin skew plates[J]. Computers and Mathematics with Applications, 2015, 70(8): 2074-2086.

[14] LI W L. Free vibration of beams with general boundary conditions[J]. Journal of Sound and Vibration, 2000,237(4):709-725.

[15] LI W L, ZHANG X F, DU J T, et al. An exact series solution for the transverse vibration of rectangular plates with general elastic boundary supports[J]. Journal of Sound and vibration, 2009,321(1/2):254-269.

[16] LEISSA A W. The free vibration of rectangular plates[J]. Journal of Sound and Vibration, 1973, 31(3): 257-293.

Vibration characteristics analysis of skew plates under elastic boundary conditions

WU Yuanfu1, WANG Jiufa2, GAO Ping2

(1. Chongqing Universtiy, Chongqing 400044, China;2. No. 710 R&D Institute, CSIC, Yichang 433003, China)

An improve Fourier series method was employed to establish the vibration model of a skew plate and to analyze the vibration characteristics of the plate under arbitrary elastic boundary conditions. The vibration displacements were expressed as the linear combination of a two-dimensional Fourier cosine series and suppelmentary series. The supplementary series were used to solve the discontinuity problems encountered for displacement partial differentials along the boundaries. So this method could be applied for arbitrary elastic boundary conditions. Based on Hamilton’s principle, the matrix form for the governing vibration equations of the plate was derived, the natural frequencies and modal shapes of the plate were obtained through solving the eigen-problem of the matrix equation. Finally, the numerical simulations were performed, the natural vibration frequencies of the plate with different boundary conditions were solved. The results were compared with those in literatures and those of FEA, the correctness of the ;proposed method was verified.

skew plates; improved Fourier series; elastic boundary condition; Hamilton’s principle

2015-12-07 修改稿收到日期：2016-03-30

吴垣甫 男，博士，1981年生

TP533

A

10.13465/j.cnki.jvs.2016.21.019