基于Popov超稳定理论的实时子结构试验MRAC控制与仿真

邓利霞， 范 武

(西南石油大学 土木工程与建筑学院，成都 610500)



基于Popov超稳定理论的实时子结构试验MRAC控制与仿真

邓利霞， 范 武

(西南石油大学 土木工程与建筑学院，成都 610500)

在实时子结构试验中，如果加载作动器不能及时、准确、稳定地实现在算法步长内的动作指令或者在加载过程中受到扰动，那么将造成试验结果的极大失真。为了避免这种情况的出现，创新的将Popov超稳定理论引入到试验的加载控制中来，设计出了一种MRAC(模型参考自适应控制)系统并通过MATLAB/Simulink进行了建模仿真。仿真结果证明了基于超稳定理论设计的MRAC系统具有良好的跟踪精度、响应速度和在线纠偏功能，满足了实时子结构试验要求。

实时子结构试验；MRAC系统；加载控制；仿真；超稳定

结构抗震试验是揭示结构抗震特性的重要手段也是结构抗震设计的基础。传统的结构抗震试验包括拟静力试验、拟动力试验和地震模拟振动台试验[1-3]。为了适应结构抗震技术的发展，日本学者基于拟动力试验的思路提出了实时子结构试验方法[4]。这种新型的结构抗震试验方法将结构的关键部分作为试验子结构，进行实时的物理加载，而其余部分作为数值子结构，通过数学模型予以模拟。实时子结构试验方法既降低了大比例尺抗震结构试验的成本，又能检验速度、加速度相关型结构或构件的性能，综合了传统抗震试验方法的优势，但同时也面临许多关键的科学问题，吸引了国内外许多学者的关注，得到了较快的发展。

加载控制的稳定性、精度问题和响应速度是实时子结构试验技术的关键问题。模型参考自适应控制系统(MRAC)是一种经典的控制方法，其被运用到涉及控制的各个行业领域。目前结构试验中大多采用电液伺服系统，对于电液伺服系统，各种机械的，液压的和电子等非线性集于一体，这种非线性系统如果采用常规的PID控制，很难达到满意的效果。而MRAC系统在满足系统精度和响应速度要求的前提下不仅能提高系统的动态性能，还能对系统参数的变化、非线性进行很大程度的适应并能在线纠偏。基于Popov超稳定理论设计的MRAC系统又是全局稳定的，所以能够满足试验加载稳、准、快的目标，提高了试验的效能。

文献[5]在试验中采用了LQR(线性二次最优)控制，在选取合理的增益下才能恰好使作动器完成积分算法步长内的动作指令，如果积分步长选取的比较小，这种控制方法就很难适用了；文献[6]虽然设计的也是MRAC系统，但其采用的是lyapunov理论。其局限性在于lyapunov函数的寻找比较困难。传统的PID控制的适应性又很差，而基于Popov理论[7]设计的MRAC系统则成功克服了以上难题。

1 MRAC系统设计

1.1 系统构建

用超稳定理论进行模型参考自适应控制(MRAC)系统设计时，要把被控对象转化成图1所示的由两个方框组成的非线性时变反馈系统，一个方框是处于前馈通道的传递函数G(s)，另一个是非线性的反馈回路φ(y,t)。u,y分别为输入和输出。

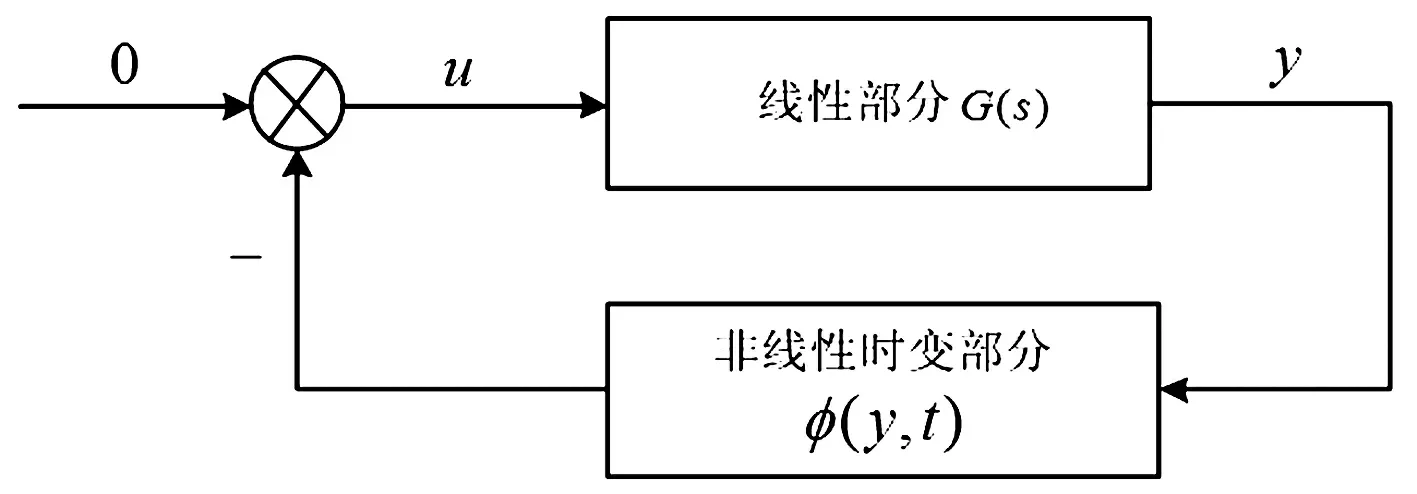
图1 非线性时变反馈系统Fig.1 The nonlinear time-varying feedback system

参考模型组成线性前向回路，具有时变非线性的被控对象和含有记忆功能的比例积分控制器组成非线性的反馈回路，如图2所示。其中r为输入信号,ym和yp分别为参考模型和被控对象的输出，e为广义误差。

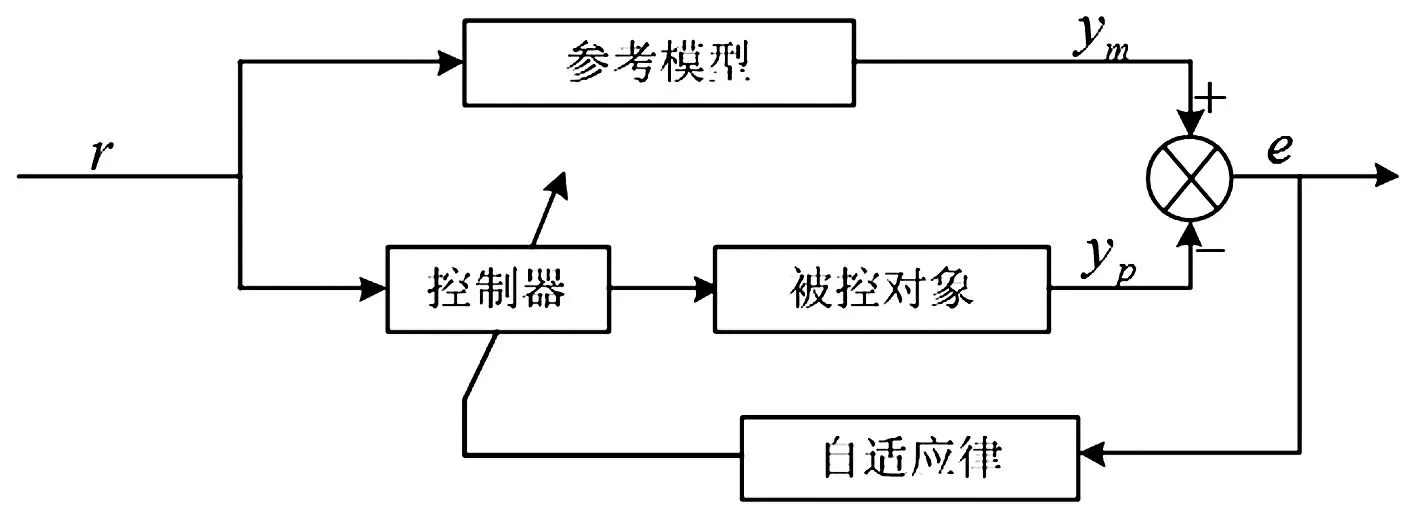
图2 MRAC系统框图Fig.2 System diagram of MRAC

1.2 自适应规律推导

1.2.1 列数学模型方程

研究对象采用文献[8]中实验子结构、作动器及控制器组合系统简化而成的一个二阶传递函数

(1)

为了使推导过程简化，假设参考模型和被控对象的极点相同，但其推导的规律同样适用极点不同的情况，在后面的仿真证明了这一点。

被控对象的数学模型：

(2)

参考模型的数学模型：

(3)

控制器：

Ge(s)=kc

(4)

广义误差：

e=ym-yp

(5)

由图2知可调系统的传递函数为：

(6)

则由式(2)、(3)、(5)得等价的误差方程：

(s2+a1s+a2)e=(bm-kcbp)r

(7)

1.2.2 求等价非线性反馈系统

对误差方程做变换得到非线性的反馈系统，其中线性定常部分位于前向通道，非线性时变部分位于反馈通道。根据Popov超稳定理论的要求等价反馈系统必须满足两个条件：① 前向通道满足正实性；② 反馈通道满足Popov积分不等式。为了满足前向通道的正实性，需要在前向通道中串入一个补偿器D[9],则设计的模型如图3所示。

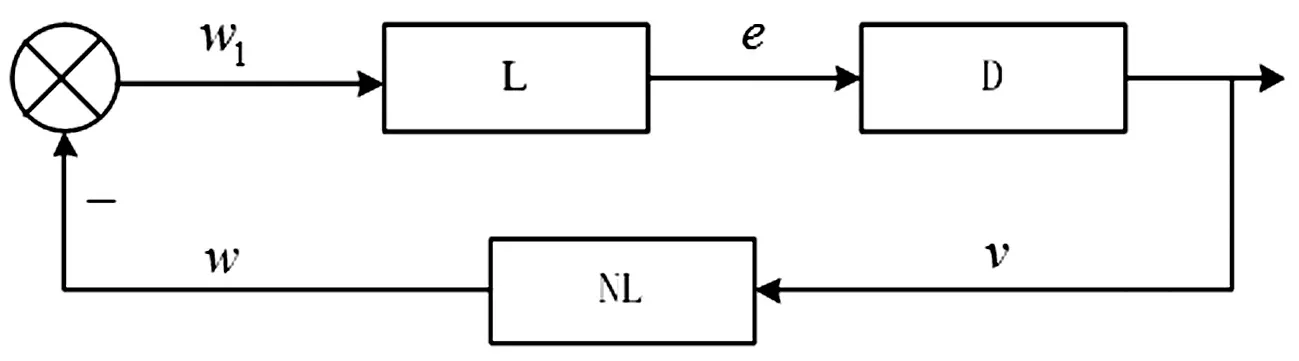
图3 等价非线性闭环系统Fig.3 Equivalent nonlinear closed loop system

线性块为：

(s2+a1s+a2)e=w1,w1=-w

(8)

反馈块为：

w=(kcbp-bm)r

(9)

则线性块函数(前向通道)：

(10)

为了前向通道的严格正实性，串入补偿器D，其输入为e，输出为v，v=De。其中：

(11)

自适应控制规律的一般形式为：

(12)

为了使反馈块的输入、输出满足popov积分不等式

(13)

将式(9)代式(13)得：

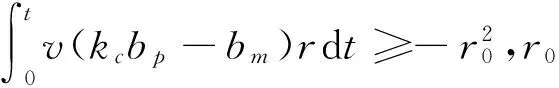
(14)

将式(12)代入式(14)得：

(15)

简化为：

(16)

(17)

1.2.3 确定D、φ1、φ2，得到自适应律

1.2.3.1 求D

根据Popov定理：前向通道满足正实性，等价系统的前向通道[10]为：

(18)

其中d0，d1为未知常数

将s=jω代入式(18)，得：

(19)

h(jω)的实部为：

(20)

使Re[h(jω)]>0，需d0>0，d1>d0/a1，串入补偿器时只要满足这两个不等式即可。

1.2.3.2 求φ1、φ2

由式(16)、式(17)求解φ1、φ2

求φ2：由式(17)取φ2=k2(t)vr，k2(t)≥0，则满足式(17)。简单取k2(t)=k2(比例放大系数)得：φ2=k2vr。

求φ1：由微积分

(21)

设f′(t)=vr

(22)

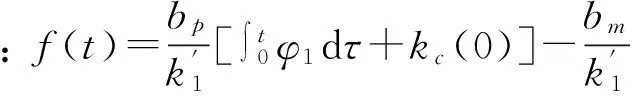
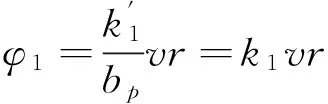
(23)

综上所述控制器[11-12]：

(24)

2 建模仿真

2.1 动力模型的阶跃响应

研究采用式(1)表达的系统二阶简化模型,根据推导出来的补偿器D和控制器kc，在Matlab/simulink中建立试验单步阶跃指令仿真系统[13-14]如图4所示。其中补偿器中常数d0、d1需满足使Re[h(jω)]>0的条件；相应的比例系数k1、k2要满足φ1、φ2的相应要求。

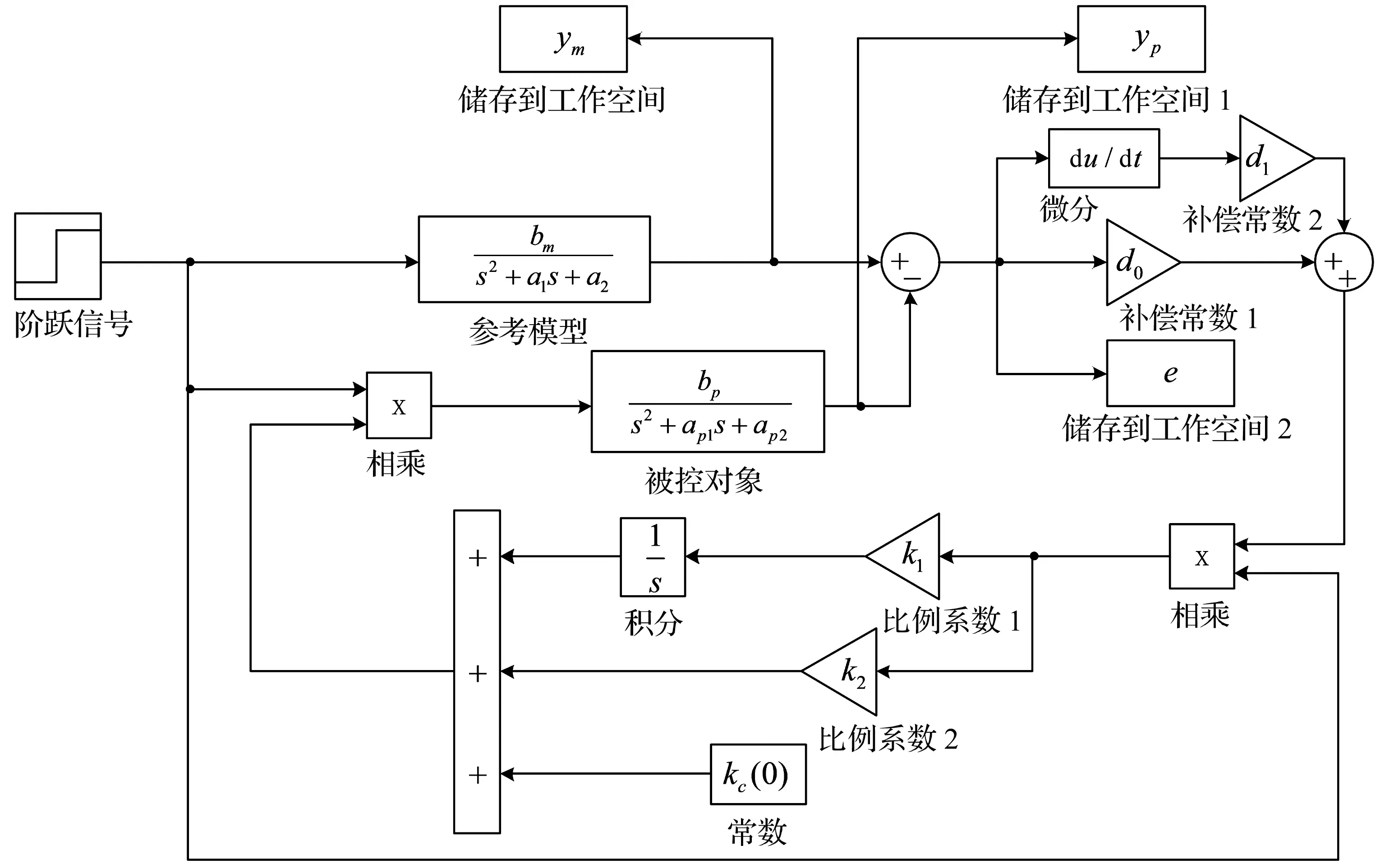
图4 系统单步控制框图Fig.4 Step control system diagram

取参考模型参数ξA=1.0,ωA=500,则参考模型的传递函数为：

(25)

被控对象参数取bp=20 000，ap1=200，ap2=20 000，系统中串入的补偿器参数选取：d0=9.5，d1=0.05，k1=1 500，k2=5.5，kc(0)=0.05，当单位越阶指令为0.4 cm、0.6 cm、0.8 cm、1 cm时，则系统的位移响应曲线如图5所示。

从图5中的四种位移指令的响应曲线可以看出设计的超稳定MRAC系统的跟踪性能和稳定性非常好，从数据上分析，在0.015 s以前系统就能完成单步的动作指令，相比文献[5]的0.04 s要小得多，大大提升了积分算法的步长缩小的空间，有效提升了试验的精度。从图形的平滑度可以看出设计的MRAC系统在阶跃指令下的动作很稳定。对比几种位移指令的响应，在调节系数k1，k2确定下来后，位移指令虽然改变，但系统依旧能够快速、稳定的到达指定位移处，这说明该MRAC调节系统具有很强的的适应性[15]。

为了证明基于超稳定理论设计MRAC系统在实时子结构试验的加载控制中是一种良好的控制方法，针对试验子结构简化的同一被控对象，分别计算出不同刚度(KE[6]和0.1KE)下超稳定MRAC系统、PID控制系统控制下的阶跃响应，比较它们的控制效果，结果如图6所示。从图中明显看出超稳定MRAC系统在刚度改变的情况下位移轨迹基本不变， 而PID控制系统则发生不稳

定且不能快速响应位移指令的现象。因此相比PID，超稳定MRAC具有较强的适应性、稳定性和响应快速性。

为了进一步体现超稳定MRAC的优越性，依旧拿同一试验子结构简化的被控对象，将其和基于lyapunov的MRAC[6]在同一阶跃指令(r=1 cm)的响应下做对比，其中增益参数的选取：超稳定MRAC依旧是上文中选取的k1=1 500，k2=5.5；基于lyapunov的MRAC参数选取为γr=4×105，γy0=4，γy1=0.08。则由两种控制方法作用下的阶跃响应如图7所示。从图7可以看出两种MRAC在响应速度上差别不大，但是在稳定性上基于lyapunov的MRAC在控制没有达到目标位移时一直在发生轻微的波动，这种波动对试验来说是不利的，所以超稳定(popov)MRAC在控制的稳定性上优于基于lyapunov的MRAC。

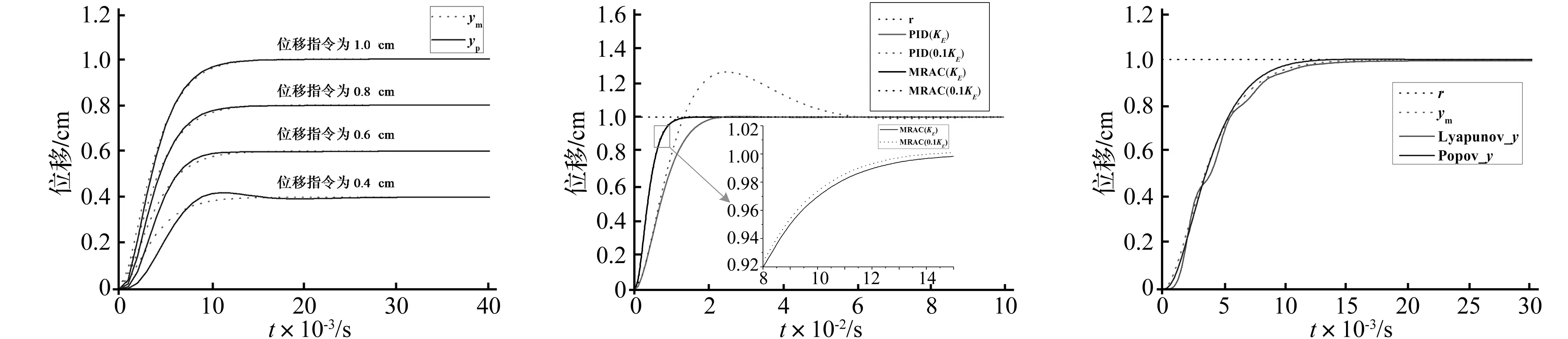
图5 几种位移指令下的位移响应Fig.5Displacementresponseofseveralstepinstruction图6 不同刚度下超稳定MRAC和PID控制的响应Fig.6TheresponseofdifferentrigidityundersuperstabilizationMRACandthePIDcontrol图7 两种MRAC的阶跃响应Fig.7StepresponseunderthetwokindsofMRAC

综上所述，在实时子结构试验的控制加载的阶跃响应中超稳定MRAC能够达到试验所期望的稳、准、快的目标，其在试验中的表现要比PID和基于lyapunov的MRAC要好。

2.2 地震作用下的响应

由于研究的是试验的加载控制采取的都是同一积分算法，所以不考虑数值积分算法的影响。在实时子结构试验中，数值子结构在离散时域上的运动方程可以写成如下形式[16]：

MNaN,i+CNvN,i+KNdN,i+RE,i=Fi

(26)

式中:M、C及K分别为数值子结构的质量、阻尼及刚度矩阵；ai、vi及di为第i步的加速度、速度及位移向量；R为反力向量；F为结构所受的外荷载向量；下标N和E分别表示数值子结构和试验子结构。根据标准中心差分法[17]的假定可知数值子结构的速度和加速度分别为

(27)

(28)

式中:Δt为积分时间步长。将式(27)与式(28)代入式(26)，整理后可以得到

(29)

试件为动力子结构，因此上式中的反力RE,i与试验子结构第i步实现的位移、速度和加速度相关，为了保证测得的RE,i尽量准确，加载装置需要带动试件实现的除了位移dE,i外，还有速度vE,i和加速度aE,i。所以加载控制系统在Δt内稳定、精确的实现相应的指令对试验十分重要。试验原理图如图8所示。

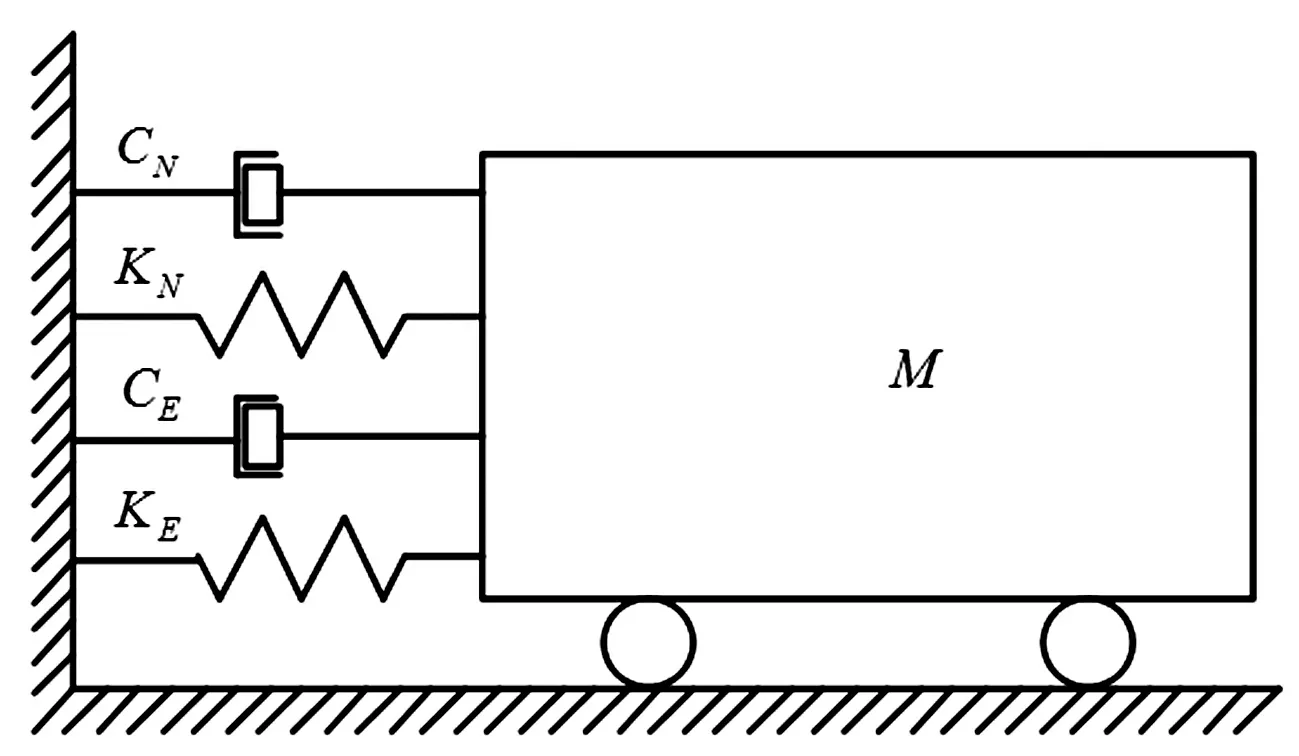
图8 单自由度实时子结构试验原理图Fig.8 Schematic diagram of real-time substructure testing with one degree

对于单自由度实时子结构试验体系，M=5 000 kg；KN=147.392 kN/m、CN=3.143 2 kNs/m分别为数值子结构的刚度系数和阻尼系数；KE=50～2 000 kN/m,CE=4.2 kNs/m分别为实验子结构的刚度系数和阻尼系数。结构的初始位移、初始速度和初始加速度均为零。仿真输入荷载为El Centro(NS,1940)地震波，峰值加速度调整为0.02 g，积分步长为Δt=0.04 s。调整系数k1=5 500,k2=15,在MATLAB/Simulink中进行仿真结果如图9所示，其中精确解是通过微分求解器(MATLAB中的LSIM命令)求得的。

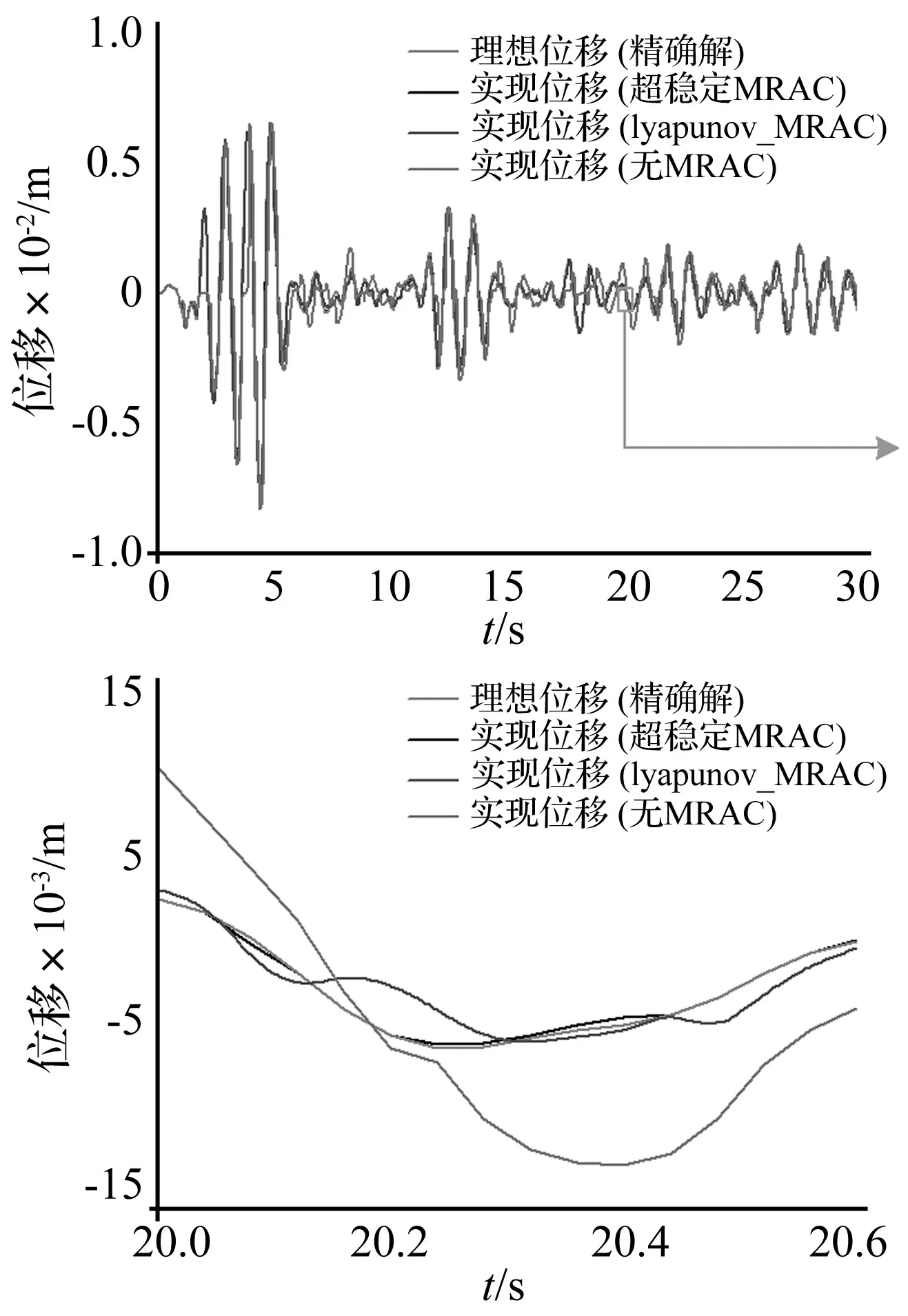
图9 超稳定MRAC控制下的仿真结果和精确解的对比Fig.9 The comparison between exact solution and the simulation’s result by Super stable MRAC

从图9中的仿真结果可以看出，超稳定MRAC、lyapunov_MRAC以及无MRAC和精确解四条位移曲线的走势中，超稳定MRAC和精确解的吻合程度最高，几乎完全重合，这种结果证明了基于Popov理论的MRAC系统可以很好的保证试验的精度和稳定性，从而可以提高试验结构的可靠性，使其更能反映结构的动力特性，从而为抗震设计提供依据。

3 结 论

基于Popov超稳定理论设计的MRAC系统在实时子结构加载控制中对指令的响应及时、稳定、精准，是一种较为优秀的控制系统，可以在试验中应用并推广。但本文得到的推导规律和应用仿真都是比较简单的，很多地方还是有待完善的，如比例系数的选取范围、改变系数对试验结果的影响以及高阶作动器控制律的推导等，这些都有待进一步继续研究。

[1] 邱法维，钱稼茹，陈志鹏. 结构抗震试验方法[M]. 北京：科学出版社，2000.

[2] 何文福，刘文光，张颖,等. 高层隔震结构地震反应振动台试验分析[J]. 振动与冲击，2008，27(8): 97-101. HE Wenfu, LIU Wenguang, ZHANG Ying, et al. High-rise structure seismic response analysis of vibration table test[J]. Journal of Vibration and Shock, 2008，27(8): 97-101.

[3] 韩强，杜修力，刘晶波,等. 多维地震作用下隔震桥梁地震反应(I)一模型结构振动台试验[J].振动与冲击，2008，27(9): 59-65. HAN Qiang, DU Xiuli, LIU Jingbo, et al. Isolation bridge seismic response under multi-dimensional earthquake(I)—model structure of shaking table test[J]. Journal of Vibration and Shock, 2008，27(9): 59-65.

[4] TAKNASHI K, NAKASHIMA M. Japanese activities on on-line testing, journal of engineering mechanics, ASCE, 1987, 113(7): 1014-1032.

[5] 张涛. 电液伺服加载系统的LQR控制及在实时子结构实验中的应用[D]. 哈尔滨：哈尔滨工业大学, 2008.

[6] 邓利霞. 实时子结构实验的自适应控制方法[D]. 哈尔滨：哈尔滨工业大学,2007.

[7] POPOV V M. Hyperstability of contorl systems. Spring Verlag, 1973

[8] 王倩颖. 实时子结构试验方法及其应用[D]. 哈尔滨：哈尔滨工业大学,2007.

[9] lANDAU I D. Ahyperstablility criterion for model reference adaptive control systems [J]. IEEE Trans. Autom. control,1969:552-555.

[10] LI Y, ZHANG K, WANG H. Aadaptive contorl theory and appliction[M]. Xi An：Northwestern Polytechnical University press, 2010:81-83.

[11] 陈复扬,姜斌.自适应控制与应用[M].北京：国防工业出版社，2009:111-121.

[12] 韩彦彬. 正定积分算子的本征值[J]. 河北大学学报(自然科学版),1986,1:18-30. HAN Yanbin. The eigenvalues of positive definite integral operator [J]. Journal of Hebei University (Natural Science Edition),1986,1:18-30.

[13] 王正林. MATLAB/Simulink与控制系统仿真[M].北京：电子工业出版社，2012.

[14] 石良臣. MATLAB/Simulink系统仿真超级学习手册[M].北京：人民邮电出版社，2014.

[15] LANDAU I D. A survey of model reference adaptive techniques—Theory and applications [J]. Automatica，1974,10(4):353-379.

[16] WU B, BAO H, OU J, et al. Stability and accuracy analysis of central difference method for real-time substructure testing[J]. Earthquake Engineering and Structural Dynamics,2005, 34: 705-718.

[17] WU B, DENG L, YANG X. Stability of central difference method for dynamic real-time substructure testing[J]. Earthquake Engineering and Structural Dynamics,2009, 38: 1649-1663.

MRAC control and simulation for real-time substructure testing based on Popov hyperstability theory

DENG Lixia, FAN Wu

(School of Civil Engineering and Architecture, Southwest Petroleum University, Chengdu 610500, China)

In real-time substructure testing, if the loading actuator cannot achieve action commands in time and correctly in an algorithm step or is disturbed in a loading process, it may cause a great distortion of test results. In order to avoid the occurrence of such a situation, Popov super stability theory was introduced into the loading control of tests. A model reference adaptive control(MRAC)system was designed and with MATLAB/Simulink, its modeling and simulation were conducted. The simulation results showed that the MRAC system designed using the super stabilitr theory has better tracking accuracy, response speed and online error-correcting function to meet the requirements of real-time substructure testing.

real-time substructure testing; MRAC system; load control; simulation; hyperstability

西南石油大学青年教师“学术过关”项目(201131010078)

2015-06-10 修改稿收到日期：2015-10-23

邓利霞 女，讲师，博士，1978年生

TU317.1;TU311.3

A

10.13465/j.cnki.jvs.2016.21.007