风突变效应对风力机振动特性影响研究

丁勤卫， 李 春,2， 叶 舟,2， 阚 威

(1.上海理工大学 能源与动力工程学院，上海 200093； 2.上海市动力工程多相流动与传热重点实验室，上海 200093)



风突变效应对风力机振动特性影响研究

丁勤卫1， 李 春1,2， 叶 舟1,2， 阚 威1

(1.上海理工大学 能源与动力工程学院，上海 200093； 2.上海市动力工程多相流动与传热重点实验室，上海 200093)

风是影响风力机气动特性和结构特性的最直接的因素，风速突变将诱发风力机更强的气动载荷。为分析风力机在高突变湍流风作用下结构动力学振动特性，以NREL实测数据为湍流风数据源，并添加拟序结构刻画风速突变，以NREL Wind PACT 1.5 MW桩柱式风力机为样机，分别研究了风力机叶片和塔架的动力学响应。结果表明：添加拟序结构前后，轮毂点处风速分形维数均在1.5左右；拟序结构的添加使得基础湍流风具有更大的风突变以及更高的湍流强度；切出风速工况，风力机叶尖位移同时为挥舞和摆振；拟序结构的添加使得叶片和塔架振动加速度成倍增加。

风力机；拟序结构；位移；振动；加速度

风能作为一种清洁的永续能源逐渐受到各国的重视，2014年中国新增装机容量达到2 303 万kW[1-2]。我国风能资源的整体特点是分布广、不稳定和能量密度相对较低[3]，风能资源相对丰富的东南沿海地区需要面对地貌复杂、气流强烈的空间不均匀性和时域风场非定常性等客观因素的巨大挑战。风力机是将风能转化成电能的设备，风力机正常运行时，来流风向改变、边界层效应、大气紊流、阵风以及上游风力机尾迹的影响，使得风力机在多数情况下处于非稳态的运行环境，突变的风作用于风力机将导致非定常的气动外载[4-5]。

早期对风力机的研究侧重于风力机气动性能的提升[6-7]，忽视了其振动性能方面的研究，近年来频繁出现的风力机损害事故使得风力机振动特性研究成为风力机研究领域内的新热点[8-9]。文献[10]考虑气弹耦合现象，对失速型600 kW风力机进行振动分析。文献[11]比较了索塔型风力机和塔架型风力机在50 a一遇阵风作用下振动响应。文献[12]通过对某3 MW风力机塔架动力响应进行计算，得到了风力机塔架在风-地震联合作用下塔架顶部振动位移和塔架底部载荷。文献[13]通过建立风力机柔性叶片气弹耦合方程，分析叶片的振动和叶根挥舞和摆振力矩，研究了柔性叶片振动对气动载荷的影响。文献[14]通过建立连续梁的偏微分方程，施加外部和内部的正弦激励，通过Galerkin数值分析方法，研究了叶片的非线性振动。由此可见，现有对风力机振动特性研究大都侧重于单一柔性部件或塔架或叶片，同时限于条件只进行定性分析而未定量比较，对风况的选择大都是普通湍流风，并未考虑极强的湍流和切变效应。

为探究突变的风对风力机振动特性影响，选择一种合适的方法建立随时间及空间变化的湍流风是仿真首先需要解决的问题。文献[15]通过大涡模拟方法，考虑大气边界层和地表粗糙度等条件，建立风电场区域的三维风场，该方法虽然空间、时间尺度均满足仿真需求，但需耗费大量的计算资源；文献[16-18]均基于测风塔收集的实际时域风速数据，分别通过自回归滑动平均模型、神经网络近似模型和模糊逻辑预测等方法得到小空间范围的风速变化规律，该方法虽然准确性较高，但对于大空间风场模型需要大量的实测数据作为近似样本，因此成本较高；文献[19]基于风电场实测时域风速数据，考虑地表粗糙度，通过气象分析方法建立整个风电场风速分布，该模型虽然准确度较高，但空间尺度过大会导致气动载荷计算误差变大；文献[20-21]基于经典的湍流风谱模型并考虑了空间相干关系建立了三维时域变化的风场，该方法理论清晰并容易实现，因此应用最为广泛。

故针对上述问题，本文首先采用NREL提出的NWTCUP湍流谱模型，同时，为表示时有发生的风速变化突然加剧的风况，在基础湍流风上加入拟序结构，以增强风速的扰动程度。通过该方法建立合适的强湍流风，对NREL Wind PACT 1.5 MW桩柱式风力机进行结构动力学仿真，分析风力机振动特性响应，以期为风力机的设计和安全性的提高提供理论参考。

1 研究方法

基于模态截断法的风力机多体动力学建模的计算方法是目前实现风力机结构动力学仿真的主流方式之一。模态截断法是现有各风力机设计软件(GH.Bladed、FAST、FLEX5等)通用的结构动力学建模方法，该方法假设风力机为有限个刚性体和柔性体的组合系统，通过形函数描述风力机柔性叶片和塔架的模态振型，叶片和塔架等连续体的变形被表示为一系列正振动模态的线性叠加，可将叶片和塔架从连续系统的无限多个自由度减小到N(N为选取的简正模态数目)，从而加快气动结构耦合计算速度。其中，由NWTC(National Wind Technology Center)针对水平轴风力机研发的开源软件FAST应用最为广泛。

FAST是耦合气动-伺服-弹性在时域求解风力机结构动力学响应的CAE软件，业已通过GL的陆上风力机气弹计算软件的认证，因此具有较高的计算精度[22]，其主要包含3个模块：气动模块(AeroDyn)、弹性模块(ElastoDyn)和伺服控制模块(ServoDyn)。其中，AeroDyn模块采用Pitt-Peters加速度势动态入流理论，求解风轮平面诱导速度；考虑Prandtl叶尖损失及叶轮损失，通过叶素动量理论结合翼型静态气动力特性求解风轮气动力，翼型动态气动特性则通过Beddoes-Leishman动态失速模型修正。在ElastoDyn模块中，通过Kane方法建立多体动力学模型，将风力机视为由叶片、低速轴和塔架等柔性体及轮毂、变速箱、高速轴、发电机和机舱等刚性体组成的多结构体系统。采用模态截断法描述叶片和塔架等柔性连续体弹性变形，假设其结构变形为一系列振动模态的线性叠加，以气动模块求解的风轮气动力作为输入激励，得到该时间步的结构动力学及运动学响应并反馈至伺服模块和气动模块。ServoDyn模块则根据弹性模块反馈信息作出相应的控制指令，主要包括调节叶片桨距角、风轮转速和高速轴转速等。具体仿真流程如图1所示，其中Tmax为仿真时间，Δt为时间步长。

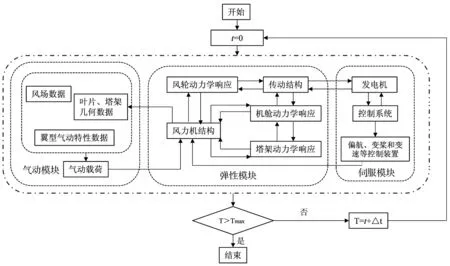
图1 动力学仿真流程图Fig.1 The flowchart of dynamic simulation

2 研究对象

本文模拟风力机为NREL WindPACT 1.5 MW风力机[23]，风力机参数见表1。

表1 风力机参数

在风力机上建立多个相对坐标系，分别为叶片坐标系{O,X,Y,Z}、轮毂坐标系{O′,X′,Y′,Z′}和塔架坐标系{O″,X″,Y″,Z″}，各结构部件坐标系如图2所示。

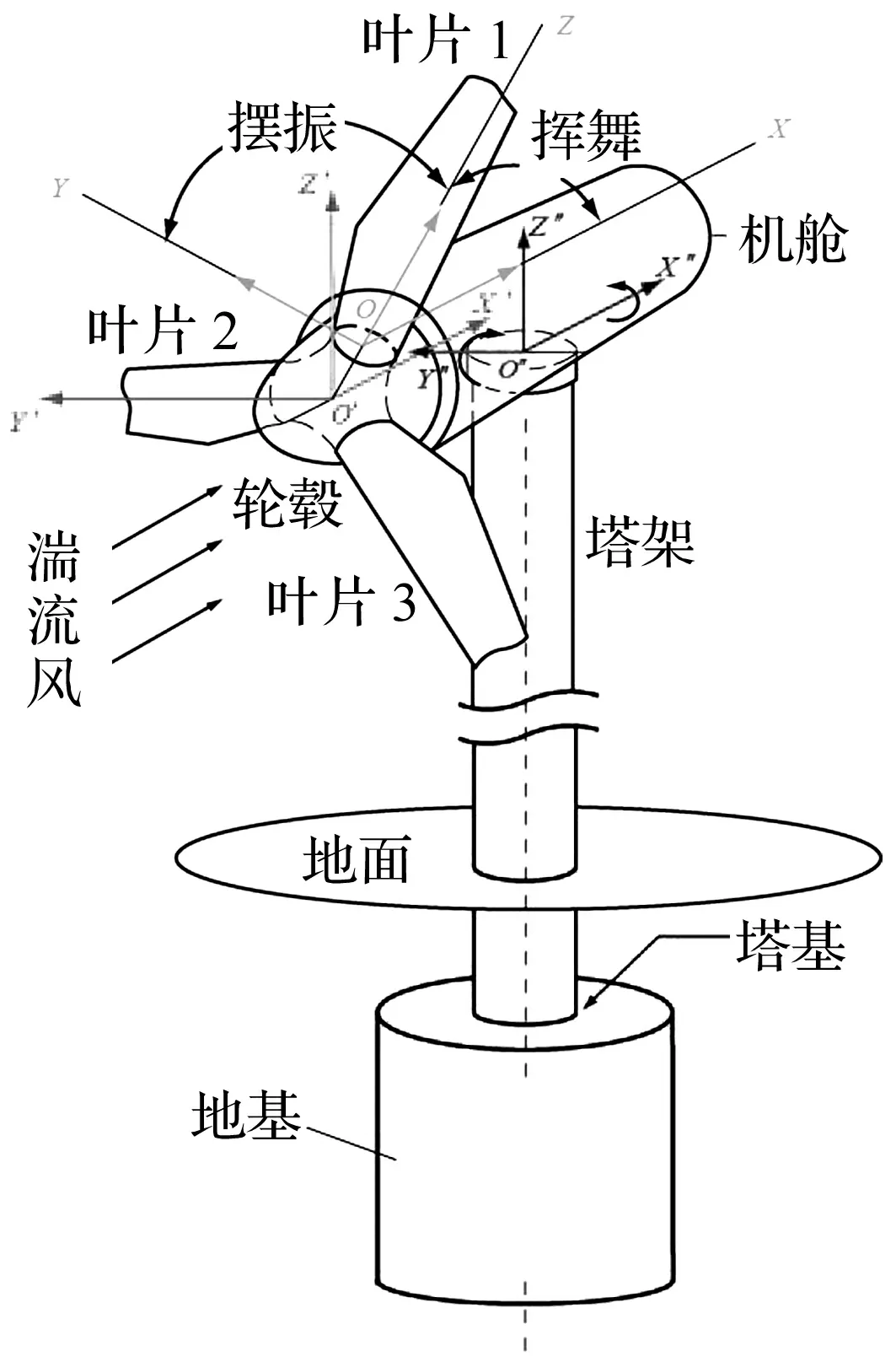
图2 风力机坐标系Fig.2 The coordinates of the model of the wind turbine

3 风场模型的建立

3.1 风谱选择

风场模型与风载荷直接相关，风场模型选择的准确性刻画风力机运行的真实环境。为真实模拟风力机在湍流风作用下柔性部件振动特性响应，本文选用由NWTC建立的NWTCUP风谱模型，该模型由实测40 Hz时间序列数据构成的湍流模型速度谱。该模型的特殊之处在于结合了SMOOTH[24-25]风谱模型和San Gorgonio风电场实测风速。其中SMOOTH风谱模型适合于地表粗糙度较低的地形，而San Gorgonio风电场与我国东海附近风电场纬度、气候和地形均十分接近，具有地表粗糙度低、能量密度高和湍流度强等特点。该风谱模型一定程度上可以代表我国东部近海湍流风。

根据风力机参数设定风场覆盖区域为149 m×149 m，如图3所示。风速分量u沿x轴正向(即垂直于风轮平面)，风速分量v沿y轴正向，风速分量w沿z轴正向。对计算域进行网格划分，共15×15个节点，轮毂中心位于中心节点。

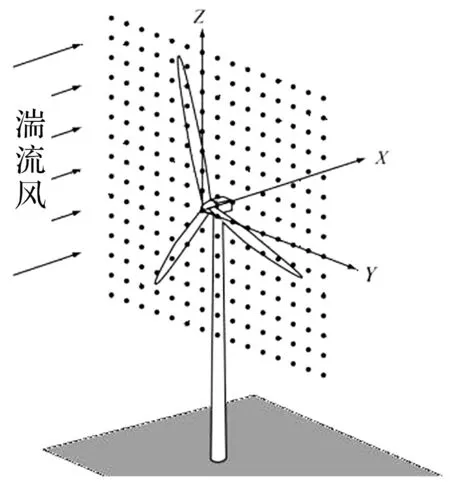
图3 风场计算域示意图Fig,3 Wind Field of Simulation

任意给定点的风速和湍流分量可用过风谱模型得到，但整个风场的风速分布情况及湍流度无法通过某一个点的风谱表示，因此，必须考虑空间点之间的相互关系，这种相互作用的关系可通过空间相干模型表示：

(1)

式中：Si,j(f)为节点i,j的互功率谱；C(Δr,f)为空间相干大小，节点之间的距离为Δr；Si,i(f)和Sj,j(f)分别为节点i和j的功率谱，在同一高度处通常可以认为二者相等

3.2 拟序结构

拟序结构是具有真实时空特征的Kelvin-Helmholtz不稳定流数值模拟结果，首先将其分割成具有无量纲速度信息的固定的无量纲尺寸片段，然后在空间和时间维度进行缩放，以确定其对绝对风速的影响大小。通过在普通湍流风上加入拟序结构以增强风速湍动，以此刻画高风突变和高湍流度。拟序结构的强弱可通过相干湍动能来描述：

(2)

式中:u′为X方向的风速波动值；v′为Y方向的风速波动值；w′为Z方向的风速波动值。

通过幂律风廓线形式描述风剪切效应，水平方向速度变化规律采用对数风廓线表示：

(3)

式中:u(z)为垂直方向速度分布；u(zhub)为轮毂处风速；z为计算节点高度；zhub为轮毂高度；u(y)为水平方向速度分布；u(yhub)为轮毂处风速；y为计算节点水平位置；z0为地表表面粗糙度，其值取0.021；ψ为垂直稳定度无量纲函数。

3.3 风场模拟结果

以轮毂中心为参考点，以该点时历平均风速24 m/s为参考风速，对选择的NWTCUP风谱模型进行傅里叶逆变换并考虑空间相干关系得到空间各个节点风速，并通过建立基础湍流风，并在150 s～450 s之间随机添加拟序结构建立更强的湍流风，共2种风况：普通湍流风(无拟序结构)、强湍流风(添加拟序结构)。图4为300 s时加入拟序结构前后风速的比较。由图4可知，加入拟序结构后空间风速分布出现了两个明显的涡，风速大小差异更大，且平均风速增大，说明添加拟序结构的有效性。

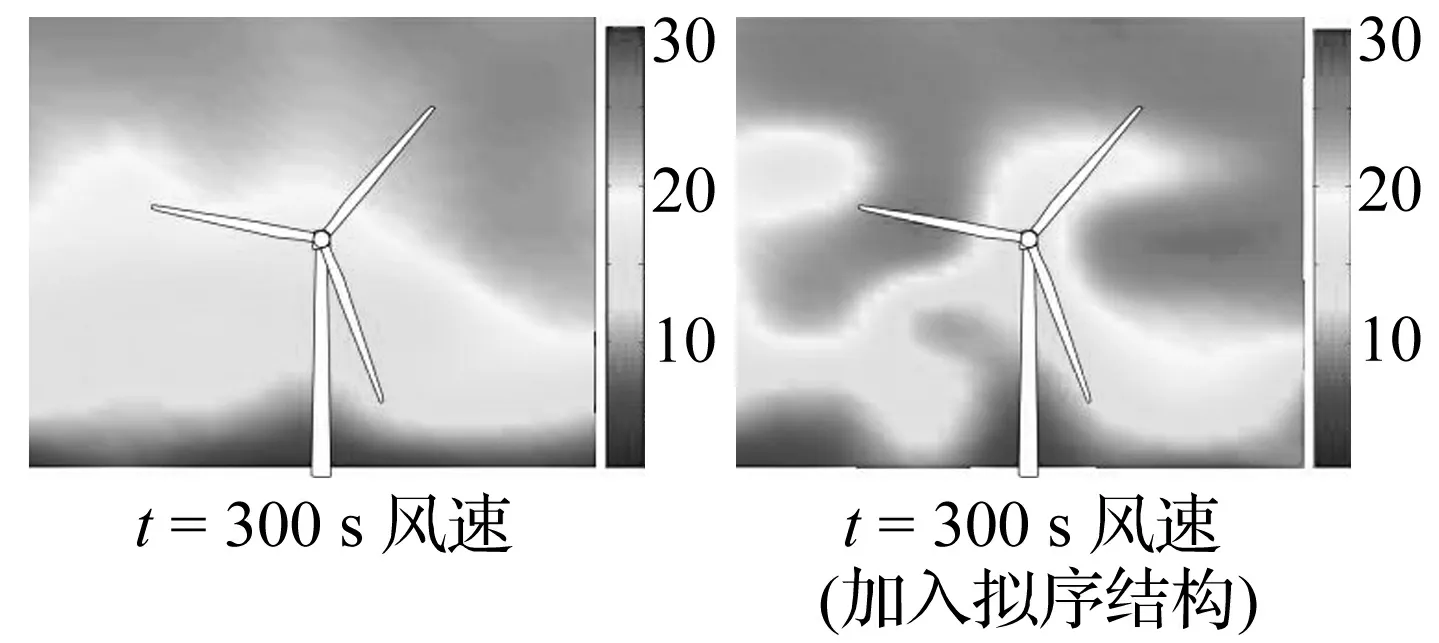
图4 加入拟序结构前后速度对比Fig.4 Wind speed of background inflow only and coherent structure added wind

两种风况在轮毂点风速在三个方向分量大小及其对比情况如图5所示。由图5可知，添加拟序结构的150 s～450 s内，三个方向的风速分量均出现了剧烈的波动，尤其是v和w，风速波动的增大不仅仅引起风速绝对大小的增加，更加剧风速方向的变化。

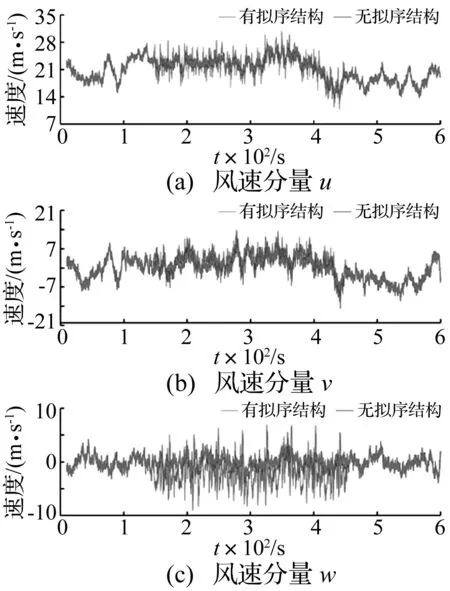
图5 轮毂高度处风速时域分布Fig.5 Velocities of wind at hub height in time domain

图6为加入拟序结构前后相干湍动能的变化对比情况，由图6可直观的看出拟序结构的添加使得相干湍动能增加翻倍。

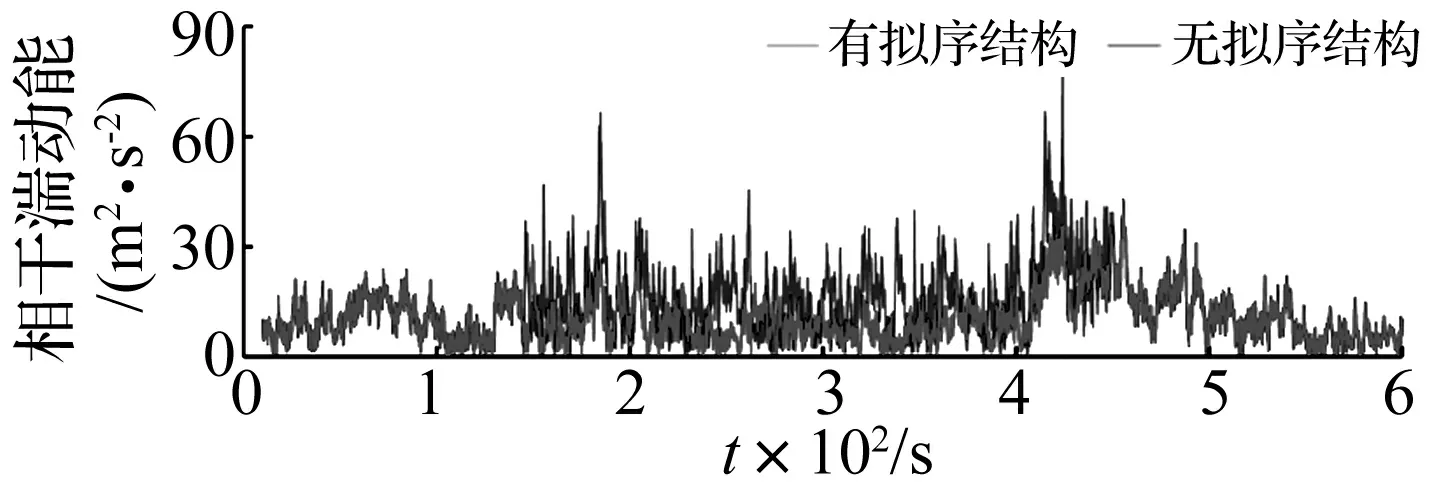
图6 轮毂点湍动能变化曲线Fig.6 The variations of wind speed at hub point

为进一步表明拟序结构添加的更接近实际风场的有效性，通过计盒维数法计算轮毂点处总风速的分形维数[26]。计算结果为：未加入拟序结构的分形维数为1.493 6，加入拟序结构后为1.508 1，二者均在1.5左右，且相差很小，表明了所建立的湍流风具有非常明显的混沌特征和自然属性，从而验证拟序结构的添加的有效性。

4 结果与分析

风力机的柔性部件主要为叶片、塔架和低速传动轴，其中低速传动轴的刚度相对较大，且在风力机运行过程中位移较小，因此，柔性结构研究重点为叶片和塔架。

4.1 计算结果可靠性验证

分别建立风速为3、7、12、18、21和25 m/s的全域稳态风，模拟时间为600 s，对应功率随风速变化如图7所示。

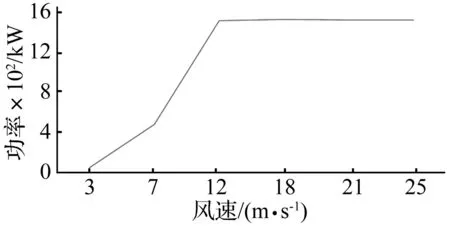
图7 功率Fig.7 Rotor power

由图7可知随风速增加平均功率逐渐增大到额定功率，在7 m/s左右出现较大功率波动当风速超过12 m/s时功率趋于稳定，这与风力机稳态运行时的情况较为接近。计算结果表明模型和求解方法能较好的反应风力机真实运行情况，较大程度验证了计算的准确性和可信度。

4.2 柔性部件结构动力学响应

图8为风力机在两种湍流风作用下叶尖位移、叶根载荷时历曲线及有无添加拟序结构的对比情况。在叶片坐标系中，X方向为纵向，Y方向为横向；叶片在XOZ平面内的运动为挥舞；在YOZ平面内的运动为摆振。

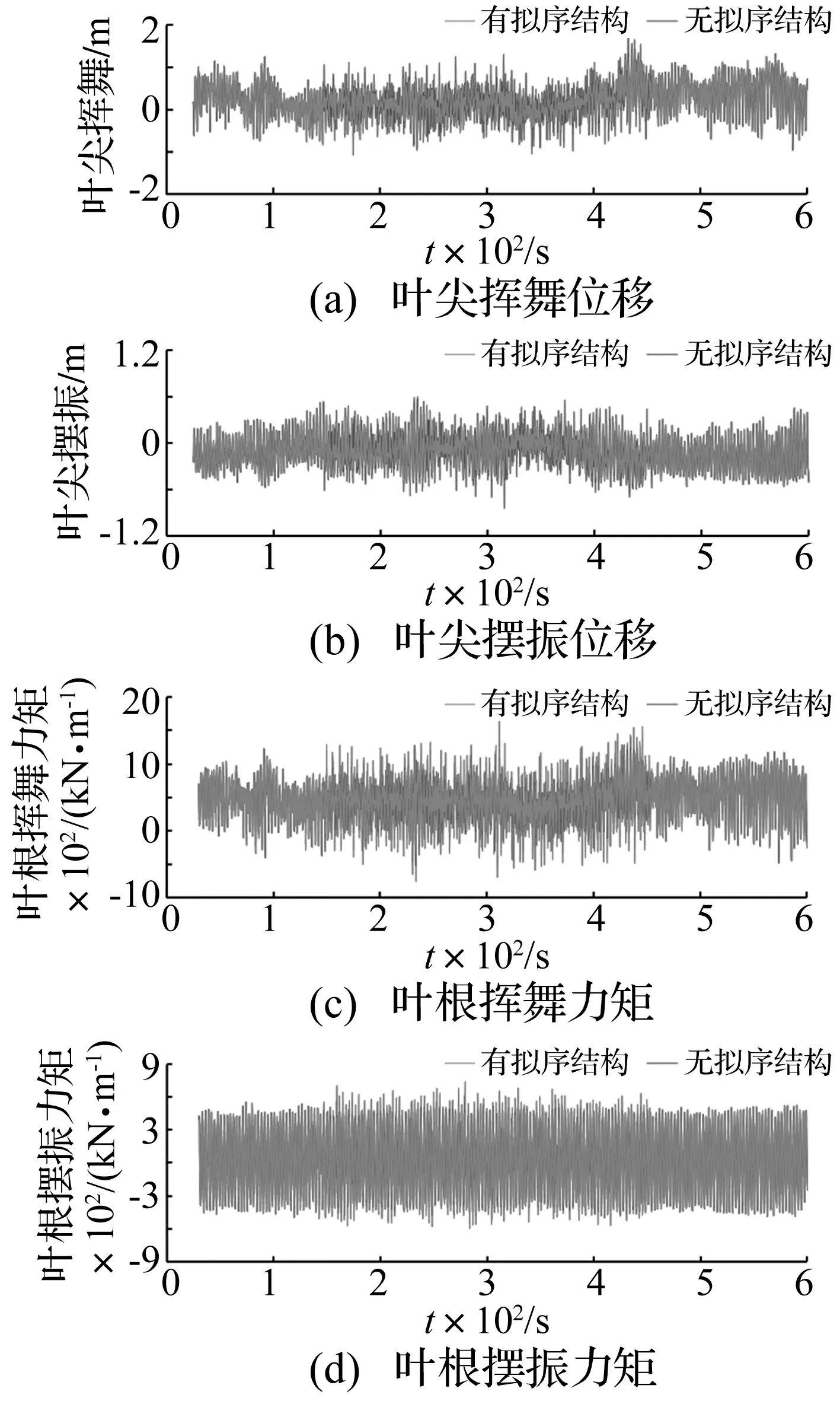
图8 叶片位移和载荷Fig.8 Deflectionand load of the blade-tip

由图8(a)和图8(b)可知，湍流风作用下，未添加拟序结构时叶尖挥舞波动范围-0.9～1.4 m，摆振波动范围-0.6～0.5 m，添加拟序结构之后，叶尖挥舞波动范围-1～1.8 m，叶尖摆振波动在-0.8～0.6 m；叶尖位移同时体现为挥舞和摆振，但挥舞方向略大于摆振方向。在添加拟序结构的150～450 s内，叶尖位移波动幅度加剧，即出现大变形时间缩短。无论是否添加拟序结构，叶尖挥舞均满足该风力机最小叶片净空设计小于3.3 m的要求[24]，进一步说明计算结果准确可信。

由图8(c)和8(d)可知，在来流风作用下，叶根处承受巨大的挥舞力矩和摆振力矩，未添加拟序结构时，叶根摆振力矩波动在-511～554 kN·m，挥舞力矩波动在-512～1 240 kN·m，添加拟序结构后，叶根摆振力矩波动-596～741 kN·m，挥舞力矩波动在-627～1 410 kN·m；波动幅度分别为未添加拟序结构时的1.25倍和1.16倍。

因风轮有着巨大的迎风面积，叶根挥舞方向力矩主要来自于气动载荷，故挥舞方向力矩高于摆振方向力矩；摆振方向力矩一部分来自气动载荷，更多的一部分来自于叶片的自重，叶片在风轮旋转平面内旋转，叶片因惯性作用产生具有周期性的力矩。总体而言，风速的突变导致气动载荷的突变，强湍流风作用下(拟序结构的添加)，叶片叶尖位移增大、叶根力矩增加，加剧了叶片的疲劳载荷并容易导致疲劳破坏。

图9为风力机在两种湍流风作用下叶尖、塔尖振动加速度时历曲线及有无添加拟序结构的对比情况。

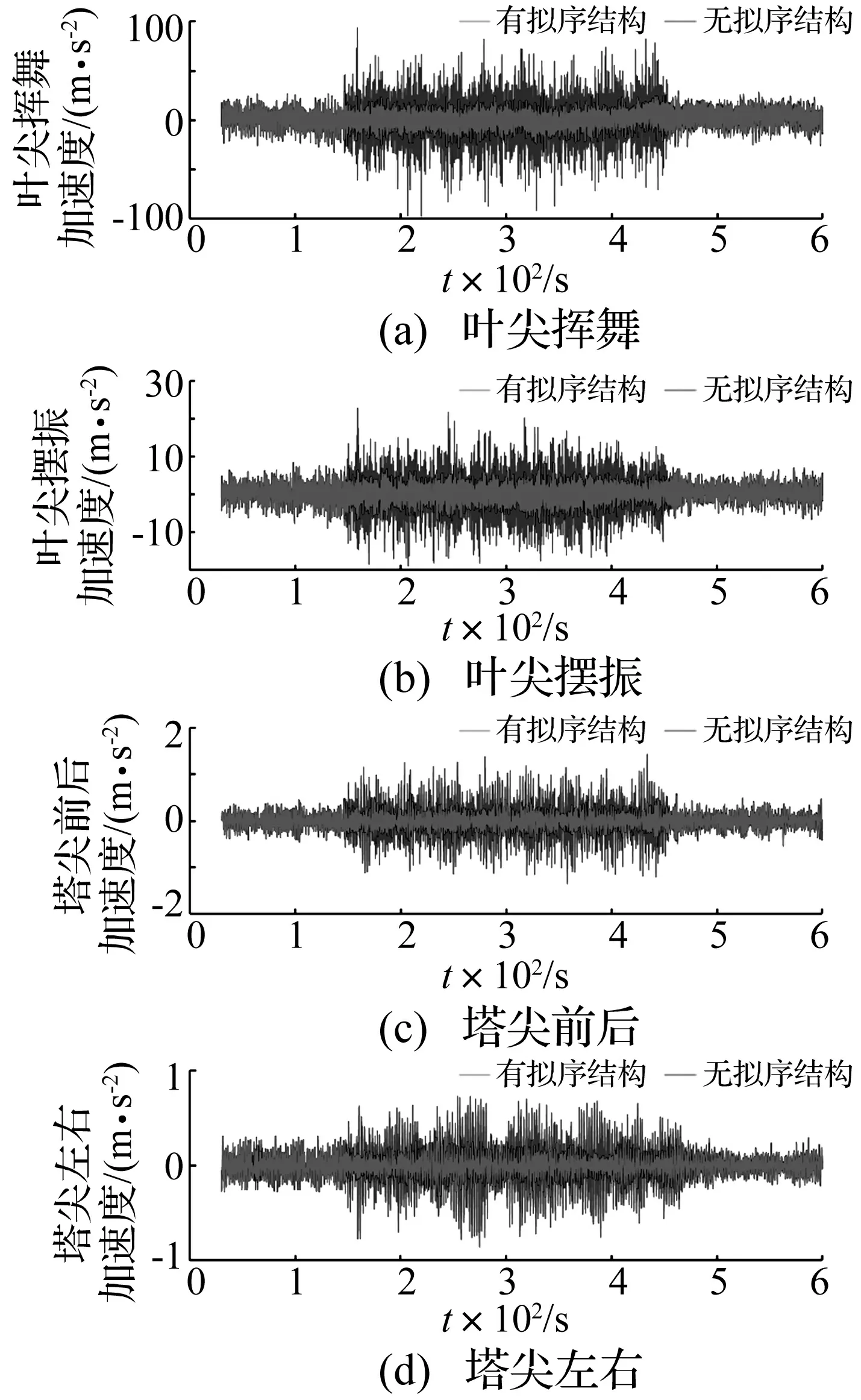
图9 叶尖和塔尖振动加速度Fig.9 Vibration acceleration of the blade-tip and tower-top

由图9可知，添加拟序结构的150～450 s内，叶尖和塔尖振动加速度波动速度和幅度剧烈增加。由图9(a)和图9(b)可知，未添加拟序结构时，叶尖挥舞振动加速度波动在-8.8～28.6 m/s2，叶尖摆振加速度波动在-8.8～8.9 m/s2；添加拟序结构后，叶尖挥舞振动加速度波动在-97.3-92.7 m/s2，摆振方向振动加速度波动在-18.9～22.8 m/s2；挥舞方向振动加速度波动幅度为未添加拟序结构的5倍，摆振方向振动加速度波动幅度约为未添加拟序结构的2倍。

由图9(c)和图9(d)可知，未添加拟序结构时，塔尖前后方向振动加速度波动在-0.6～0.9 m/s2，塔尖左右方向振动加速度波动在-0.4～0.4 m/s2；添加拟序结构后，塔尖前后振动加速度波动在-1.4～1.4 m/s2，波动幅度约为未添加拟序结构时的2倍，塔尖左右振动加速度波动在-0.9～0.7 m/s2，波动幅度约为未添加拟序结构时的2倍。

叶尖振动加速度挥舞方向大于摆振方向，这主要是因为挥舞方向叶片所受气动载荷(风轮轴向推力)较大，挥舞方向更容易发生形变及运动；塔尖方向振动加速度在前后方向和左右方向较接近；对比叶尖和塔尖振动加速度可知，叶尖振动加速度要远远大于塔尖振动加速度，这主要是因为塔尖刚度较大，与叶片相比不易形变。因叶片属柔性构件，同时叶片上的气动载荷和叶片的运动是耦合的，故气动载荷波动剧烈时，叶片振动会迅速加剧，同时作用在塔尖处的加速度也是迅速加剧。

5 结 论

基于NWTCUP湍流风谱模型建立了基础湍流风场，通过对基础湍流风添加逆序结构，构建了湍动剧烈的湍流风场作为风力机动力学仿真环境，以NREL Wind PACT 1.5 MW桩柱式风力机为样机，模拟风力机的结构动力学响应，分析了风力机柔性部件即叶片和塔架的位移和振动特性，得出结论如下：

(1) 拟序结构的添加可导致更大的风速突变、更强的湍流度效应，使风具有更高的湍动能，其分形维数为1.508 1，具有明显的分形特征和混沌特性，表明模型建立的准确性即拟序结构添加的有效性；

(2) 对设定风速(切出风速附近)，叶尖位移同时体现为挥舞和摆振，但挥舞方向位移大于摆振方向；挥舞方向叶根力矩大于摆振方向叶根力矩；高风突变、高湍流度加剧了叶根处疲劳载荷；

(3) 拟序结构的添加使得叶片和塔架的振动较之无拟序结构有了成倍的增加，振动的加剧可以诱发颤振进而导致叶片和塔架的损毁，因此，风力机设计时应不仅仅考虑最大风速，更应该考虑风突变效应。

[1] Global Wind Energy Council. Global wind statitics 2014[R]. Global Wind Energy Council，2015.

[2] 张亮，吴海涛，荆丰梅，等.海上漂浮式风力机研究进展及发展趋势[J].海洋技术，2010，29(4)：22-27. ZHANG Liang, WU Haitao, JING Fengmei, et al. Study on offshore floating wind turbine and its development[J]. Ocean Technology, 2010, 29(4):22-27.

[3] 李春，叶舟，高伟，等．现代陆海风力机计算域仿真[M]．上海：上海科学技术出版社，2012.

[4] 周文平，唐胜利，吕红. 风剪切和动态来流对水平轴风力机尾迹和气动性能的影响[J]. 中国电机工程学报，2010，32(14)：122-127. ZHOU Wenping, TANG Shengli, LÜ Hong. Effect of transient wind shear and dynamic inflow on the wake structure and performance of horizontal axis wind turbine[J]. Proceedings of the CSEE, 2010, 32(14):122-127.

[5] 李本立，宋宪耕，贺德馨，等. 风力机结构动力学[M].北京：北京航空航天大学出版社，1999：162-165.

[6] HABALI S M, SALCH I A. Design and testing of small mixed airfoil wind turbine blades [J]. Renewable Energy, 1995, 6(2):161-169.

[7] FUGLSANG P, BAK C. Development of the risø wind turbine airfoils [J]. Wind Energy, 2004(7):145-162.

[8] GANERIWALA S N, YANG J, RICHARDON M. Using modal analysis for detecting cracks in wind turbine blades [J]. Sound and Vibration, 2011,45(5):10-13.

[9] KUSNICK J F. Vertical axis wind turbine operational modal analysis in sheared wind flow [C]//Conference Proceedings of the Society for Experimental Mechanics Series, 2012, 2:333-344.

[10] 金鑫，何玉林，刘桦. 基于Pitt-peters理论的风力发电机振动分析[J].工程力学，2008，25(7)：28-33. JIN Xin, HE Yulin, LIU Hua. Vibration analysis of wind turbine based on Pitt-peters theory [J]. Engineering Mechanics, 2008, 25(7):28-33.

[11] 章子华，刘国华，王振宇，等.抗台风的索塔型风机可行性研究[J].东南大学学报(自然科学版)，2009,39(增刊2)：179-185. ZHANG Zihua, LIU Guohua, WANG Zhenyu, et al. Feasibility study of anti-strong-wind cable-tower structure[J]. Journal of Southeast University (Nature Science Edition), 2009, 39(Sup2):179-185.

[12] 曹必锋，衣传宝.风力机塔架在风-地震作用下的动力响应[J].噪声与振动控制，2014，34(4)：205-209. CAO Bifeng, YI Chuanbao. Dynamic response analysis wind turbine towers under wind and earthquake combined loadings[J]. Noise and Vibration Control, 2014, 34(4):205-209.

[13] 徐磊，李德源，莫文威，等.基于非线性气弹耦合模型的风力机柔性叶片随机响应分析[J].振动与冲击，2015，34(10)：20-27. XU Lei, LI Deyuan, MO Wenwei, et al. Random response analysis for the flexible blade of a wind turbine based on nonlinear aero-elastic coupled model[J]. Journal of Vibration and Shock, 2015, 34(10): 20-27.

[14] LI L, LI Y H, LIU Q K, et al. Flapwise non-linear dynamics of wind turbine blades with both external and internal resonances[C]//International Journal of Non-linear Mechanics, 2014.

[15] FLEMING P, GEBRAAD P, VAN WINGERDEN J W, et al. The SOWFA super-controller: A high-fidelity tool for evaluating wind plant control approaches[C]//Proceedings of the EWEA Annual Meeting, Vienna, Austria. 2013.

[16] BOSSANYI E. Short-term stochastic wind prediction and possible control applications[C]//Proceedings of the Delphi workshop on wind energy applications. 1985.

[17] BILGILI M, SAHIN B, YASAR A. Application of artificial neural networks for the wind speed prediction of target station using reference stations data[J]. Renewable Energy, 2007, 32(14): 2350-2360.

[18] DAMOUSIS I G, ALEXIADIS M C, THEOCHARIS J B, et al. A fuzzy model for wind speed prediction and power generation in wind parks using spatial correlation[J]. Energy Conversion, IEEE Transactions on, 2004, 19(2): 352-361.

[19] RATHMANN O, MORTENSEN N G, LANDBERG L. The numerical wind atlas-the KAMM/WAsP method[R]. Ris? National Laboratory, 2001.

[20] 岳一松，蔡旭. 风场与风力机模拟系统的设计与实现[J]. 电机与控制应用，2008，35(4)：17-21. YUE Yisong，CAI Xu．Design and actualization of wind farm and wind turbine imitation system[J]．Electric Machines & Control Application．2008，35(4)：17-21．

[21] 陈晓明．风场与风力机尾流模型研究[D]．兰州：兰州理工大学，2010．

[22] BUHI JR M L, MANJOCK A. A comparison of wind turbine aeroelastic codes used for certification[R]. NREL/CP-500-39113,UAS,2006.

[23] SMITH K．WindPACT Turbine design scaling studies technical area 2: turbine, rotor, and blade logistics[R]．USA: National Renewable Energy Laboratory, 2001．

[24] HØJSTRUP J. Velocity spectra in the unstable planetary boundary layer[J]. Journal of the Atmospheric Sciences, 1982, 39(10): 2239-2248.

[25] OLESEN H R, LARSEN S E, HØJSTRUP J. Modelling velocity spectra in the lower part of the planetary boundary layer[J]. Boundary-Layer Meteorology, 1984, 29(3): 285-312.

[26] CHANG T P, KO H H, LIU F J, et al. Fractal dimension of wind speed time series[J]. Applied Energy, 2012, 93: 742-749.

Effects of wind gust on a wind turbine’s vibration characteristics

DING Qinwei1, LI Chun1,2, YE Zhou1,2, KAN Wei1

(1. School of Energy and Power Engineering, University of Shanghai for Science and Technology，Shanghai 200093, China;2. Shanghai Key Laboratory of Multiphase Flow and Heat Transfer in Power Engineering, Shanghai 200093, China)

A wind turbine suffers from complex environmental conditions and wind is the most important and direct factor that can affect its aerodynamic and structural characteristics. Abrupt wind speed change may lead to higher aerodynamic loads. In order to analyze the structural dynamic characteristics of a wind turbine operating under the action of a strong turbulent wind, simulations were performed with a NREL WindPACT 1.5 MW land-based wind turbine model to study dynamic responses of the wind turbine’s blades and tower. The results slowed that before and after adding a coherent structure, fractal dimensions of wind speed at hub point are both around 1.5; adding a coherent structure into a turbulent flow can cause a higher wind speed change and a stronger turbulent intensity, compared with the basic turbulent wind; when the wind achieves an ultimate speed, the wind turbine’s blades have both in-plane and out-plane vibrations; turbulent wind with a coherent structure can make vibration accelerations of blades and tower foldincrease.

wind turbine; coherent structure; deflection; vibration; acceleration

国家自然科学基金(E51176129)；上海市教育委员会科研创新(重点)(13ZZ120,13YZ066)；教育部高等学校博士学科点专项科研基金(博导)(20123120110008);上海市科委项目资助(13DZ2260900)

2015-06-08 修改稿收到日期：2015-11-02

丁勤卫 男，博士生，1990年4月生

李春 男，博士，教授,博士生导师，1963年2月生

TK83

A

10.13465/j.cnki.jvs.2016.21.008