把握创新背景透析条件关系——以“集合”为例谈创新问题的解答

☉江苏省栟茶高级中学 吴徕斌

把握创新背景透析条件关系
——以“集合”为例谈创新问题的解答

☉江苏省栟茶高级中学 吴徕斌

由于创新问题能有效考查考生的阅读理解能力、化归转化能力及灵活运用所学知识解答问题的能力，因此成为高考亮点内容，也是必考内容.分析近几年各省市的高考试题不难发现创新问题的考查，常以压轴题或把关题的形式出现.大部分考生对此类问题一筹莫展，究其原因，是因为创新问题常以新背景、新定义的形式考查，而学生对新内容的理解不透彻，未能准确把握问题求解的关键所致.下面以一道集合创新题为例，从概念理解、条件审视等角度对问题进行分析，以期对同学们处理此类问题有所帮助.

一、题目展示

引例给定正整数n（n≥3），集合Un=｛1，2，3，…，n｝.若存在集合A、B、C，同时满足下面的三个条件：

①Un=A∪B∪C，A∩B=B∩C=A∩C=∅；

②集合A中的元素都为奇数，集合B中的元素都为偶数，所有能被3整除的数都在集合C中（集合C中还可以包含其他数）；

③集合A、B、C中各元素之和分别为SA，SB，SC，有SA= SB=SC.则称集合Un为可分集合.

（1）已知U8为可分集合，写出相应的一组满足条件的集合A、B、C；

（2）证明：若n是3的倍数，则Un不是可分集合；

（3）若Un为可分集合且n为奇数，求n的最小值.

集合是高中数学的基础概念，也是重要概念之一，以集合为视角的命题背景新颖、构思巧妙、逻辑性强.能有效考查考生的思维能力、运算能力等综合素质，还对考生的阅读理解能力、分析和解决问题的能力做出考查.此类创新题型突破常规题型的模式，形式丰富，备受命题人关注.同时，它取材广泛、时代性强、无固定套路，从侧面体现了考试的公平性.所以，在平时的教学或学习中，加强对创新题型的研究和训练，不但是备考的一项基本内容，也有利于学生自身综合素质的提高.

此类题的解答，前提是要求学生具备创新意识，对

问题的“观察、猜测、抽象、概括、证明”是发现问题和解决问题的重要途径.对数学知识的迁移、整合、融会的程度越高，显示出的创新意识也就越强，也就越容易找到解决问题的突破口.

二、条件审视

解答此类问题时，学生看到题目后就一脸茫然，甚至有些学生根本没有看懂题，不知所给的概念有什么涵义、不知所给的条件如何运用.出现这种情况除对自己所学基础知识掌握不扎实外，一个重要的原因就是阅读和理解能力较差.因此对于创新问题的求解，理解问题的本质和内涵是问题顺利求解的关键.

对本题所给概念、条件的理解可从如下几个角度来审视：

（1）题目中给出了三个条件，其中的已知与未知的根本不同是什么？这里的逻辑关系是什么？三个条件，应该先满足哪一个或哪两个？这样认为的根据是什么？

（2）对于集合问题的处理，要弄清分析集合问题的几个维度，如元素关系，数量关系等.

（3）对于一个陌生问题的处理，我们可以从动手实验开始，选择一些特殊的集合来加深对新定义的认识和理解.

通过充分审视条件不难发现，①、②属于定义性的条件，条件③反映了集合之间的数理关系.因此，在问题的具体求解中可先使所要判断的集合满足条件①、②，再去验证条件③满足与否.

具体分析、解答过程如下.

三、问题解答

此类试题的命制一般含有2～3问，难度逐渐递增.其中第（1）问属于送分题，只要读懂新概念的含义、明白所给条件之间的关系，即可顺利求解.另外在问题解答中还要注意前后两问之间的关系，前一问的结论有可能就是后一问的条件.因此解题中要准确把握、合理利用.

（1）依照题意，可以取A=｛5，7｝，B=｛4，8｝，C=｛1，2，3，6｝.验证可知满足条件.

第一问为下面的问题做铺垫，如何体会呢？请同学们思考.

（2）条件中给出具有的数理关系，因此可以抓住集合中元素的和，即SA=SB=SC这一关键点寻找思维突破口.对于缺少的具体研究对象，可创造条件，利用反证法得出矛盾，即可证明.

假设存在n是3的倍数且Un是可分集合.

设n=3k，则依照条件②可知｛3，6…，3k｝⊆C，而集合C中还可能含有其他数，所以

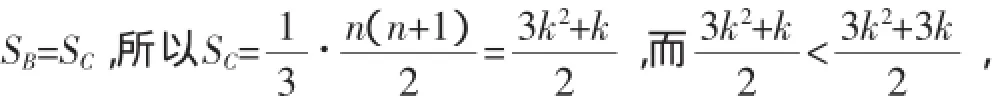
集合Un中的n个数之和为由条件③知SA=与矛盾，所以n是3的倍数时，Un一定不是可分集合.

当n为奇数时，n+1为偶数，而n（n+1）=12m，所以一定有n+1既是3的倍数，又是4的倍数，所以n+1=12k，所以n=12k-1，k∈N*.

定义集合D=｛1，5，7，11，…｝，即集合D由集合Un中所有不是3的倍数的奇数组成；

定义集合E=｛2，4，8，10，…｝，即集合E由集合Un中所有不是3的倍数的偶数组成.

根据集合A、B、C的性质知道，集合A⊆D，B⊆E，此时集合D，E中的元素之和都是24k2，此时Un中所有3的倍数的和为

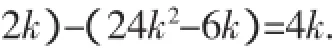
显然必须从集合D，E中各取出一些元素，这些元素的和都是2k，所以从集合D=｛1，5，7，11，…｝中必须取偶数个元素放到集合C中，所以2k≥6，所以k≥3，此时n≥35.

而令集合A=｛7，11，13，17，19，23，25，29，31，35｝；集合B=｛8，10，14，16，20，22，26，28，32，34｝；

集合C=｛3，6，9，12，15，18，21，24，27，30，33，1，5，2，4｝.

检验可知，此时U35是可分集合，所以n的最小值为35.

注意：“反证法”是逻辑推理证明中常用且有效的方法，应用中要准确假设、合情推理.另外解答中在得出n= 12k-1，k∈N*后，利用穷举法，由k=1，2，3，…，得n=11，23，35，…，在说明11，23不满足，35满足条件时，注意必须要严格地说明11、23为什不行.

四、变式演练

变式已知集合Ωn=｛X|X=（x1，x2，…，xi，…，xn），xi∈｛0，1｝，i=1，2，…，n｝，其中n≥3.

∀X=（x1，x2，…，xi，…，xn）∈Ωn，称xi为X的第i个坐标分量.若S⊆Ωn，且满足如下两条性质：

①S中元素个数不少于4个；

②∀X，Y，Z∈S，存在m∈｛1，2，…，n｝，使得X，Y，Z的第m个坐标分量都是1.则称S为Ωn的一个好子集.

（1）若S=｛X，Y，Z，W｝为Ω3的一个好子集，且X=（1，1，0），Y=（1，0，1），写出Z，W；

（2）若S为Ωn的一个好子集，求证：S中元素个数不超过2n-1；

（3）若S为Ωn的一个好子集且S中恰好有2n-1个元素时，求证：一定存在唯一一个k∈｛1，2，…，n｝，使得S中所有元素的第k个坐标分量都是1.

解析：（1）Z=（1，0，0），W=（1，1，1）.

（2）对于X⊆Ωn，考虑元素X′=（1-x1，1-x2，…，1-xi，…，1-xn）.

显然，X′∈Ωn，∀X，Y，X′，对于任意的i∈｛1，2，…，n｝，xi，yi，1-xi不可能都为1，可得X，X′不可能都在好子集S中.

又因为取定X，则X′一定存在且唯一，而且X≠X′，且由X的定义可知∀X，Y∈Ωn，X′=Y′⇔X=Y.

这样，集合S中元素的个数一定小于或等于集合Ωn中元素个数的一半，而集合Ωn中元素个数为2n，所以S中元素个数不超过2n-1.

（3）∀X=（x1，x2，…，xn-1，xn），Y=（y1，y2，…，yn-1，yn）∈Ωn，定义元素X，Y的乘积为XY=（x1y1，x2y2，…，xn-1yn-1，xnyn），显然XY∈Ωn.

证明：“对任意的X=（x1，x2，…，xn-1，xn）∈S，Y=（y1，y2，…，yn-1，yn）∈S，都有XY∈S.”

假设存在X，Y∈S，使得XY∉S，则由第（2）问可知（XY）′=（1-x1y1，1-x2y2，…，1-xn-1yn-1，1-xnyn）∈S.

此时，对于任意的k∈｛1，2，…，n｝，xk，yk，1-xkyk不可能同时为1，与题目条件矛盾，所以XY∈S.

因为S中只有2n-1个元素，我们记Z=（z1，z2，…，zn-1，zn）为S中所有元素的乘积.

根据上面的结论，我们知道Z=（z1，z2，…，zn-1，zn）∈S，显然这个元素的坐标分量不能都为0，那么不妨设zk=1.

根据Z的定义，可以知道S中所有元素的k坐标分量都为1.

下面再证明k的唯一性：

若还有zt=1，即S中所有元素的t坐标分量都为1，所以此时集合S中元素个数至多为2n-2个，矛盾.

所以结论成立.

注：本题虽然形式新颖，但通过准确阅读理题意，不难发现我们熟悉的面孔.以n维坐标系为背景，以集合为形式.问题的求解中除注意新定义的本质外，要准确把握全集、子集、元素之间的关系进行推理.

综上，解答好集合创新问题要重视数学核心概念的理解与准确运用，教师在评时的解题教学中可通过为学生创设一些理解概念的情境，训练学生充分理解概念，学会用概念解题，进而不断培养其对新概念、新知识的阅读和理解能力.这里的新知识可以是新的定理、新的方法、新的公式、新的图式、新的规则等.当然这里所说的“新”，往往只是新在形式，解题中只要把握集合的本质，即可化生为熟、化抽象为具体.通过这样的内容来训练学生对题目信息进行收集、提炼、加工、整理的能力.对阅读的内容进行概括和理解，看清问题的本质，运用合情推理和演绎推理等方法解决一些新的数学问题.另外要加强创新意识的培养，教学中以问题为出发点，通过对典型试题的分析，让学生体会创新试题的解决途径和思考方法，并归纳出解题步骤，即从新情境问题中获取信息——分析处理信息——转化为数学问题——获得原问题答案.随着高中数学课程改革的不断推进，考查学生独立获取新知识的学习型试题仍会不断地出现在高考命题中，望广大师生给予足够的重视.

1.石深敏.高考集合题的创新方式与复习对策［J］.中学数学（上），2012（7）.F