椭圆背景下的线线平行证明一例

☉安徽省太和中学 阮飞

椭圆背景下的线线平行证明一例

☉安徽省太和中学 阮飞

著名数学教育家波利亚说过：“没有一道题是可以解决得十全十美的，总剩下些工作要做，经过充分的探讨与研究，总会有点滴的发现，总能改进这个解答，而且在任何情况下，我们都能提高自己对这个解答的理解水平.”

——题记

一、问题的提出

已知两条曲线E1=1（a＞b＞0，x＞0）和E2，过原点O的两条不同直线l1和 l2，l1与E1，E2分别交于A1，A2两点，l2与E1，E2分别交于B1，B2两点.证明：A1B1∥A2B2.

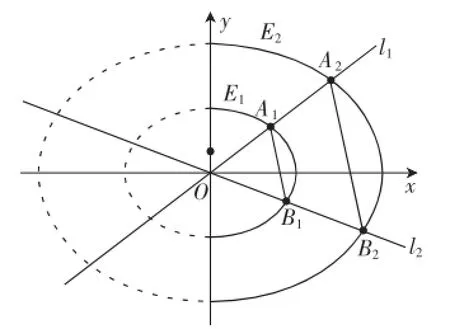
图1

如图1，不难发现曲线E1和E2分别是离心率相等的两椭圆=1（a＞b＞0）和1（a＞b＞0，λ＞1）的一部分.试题以椭圆的相似性为背景，突出椭圆方程的

考查；渗透数形结合的思想、函数与方程的思想；强调解析几何的基本方法——坐标法、向量的工具性.题目融平面向量、平面几何、解析几何知识于一体，目的是考查知识综合运用能力.

二、问题的探索

要证明两条不同的直线平行，教材中给出的方法有：证明两条直线的方向向量平行、两条直线的斜率相等（要判断斜率是否存在）、利用平面几何知识.

1.证明两条直线的方向向量平行

必修4教材中给出的方法：若直线A1B1，A2B2的方向向量分别为，要证AB∥AB，1122只需证，只需证

证法1：设直线l1，l2的方程分别为y=k1x，y=k2x（k1，k2≠0），

同理可得B1

由于直线l1过原点，A1，A2两点在l1上，故.通过设A1（x1，y1），A2（mx1，my1），可使用“设而不求”的方法.

证法2：A1，A2两点在直线l1上，可设A1（x1，y1），A2（mx1，my1）（m＞0），

同理可设B1（x2，y2），B2（nx2，ny2）（n＞0），且n=λ.

所以A2（λx1，λy1），B2（λx2，λy2），

另外，结合选修4-4教材中椭圆的参数方程，我们可以把椭圆上的点的坐标设成参数方程的形式.

证法3：由题意可设A1（acosα，bsinα）

因为A1，A2在直线l1上，所以

同理可设B1（acosβ，bsinβ）

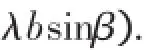
当然，我们也可以通过证明两条不同直线的法向量平行来证明两直线平行.有兴趣的读者不妨一试.

2.证明两条斜率存在的直线的斜率相等

必修2教材中给出的结论：若两条不同直线l1，l2的斜率分别为k1，k2，l1∥l2⇔k1=k2.

结合证法2，我们有证法4：

由证法2知，A1（x1，y1），B1（x2，y2），A2（λx1，λy1），B2（λx2，λy2）.

（1）当x2-x1≠0时，kA1B1=

所以kA1B1=kA2B2，A1B1//A2B2.

（2）当x2-x1=0时，A1B1⊥x轴，A2B2⊥x轴，故A1B1∥A2B2.

综合（1）（2）知，A1B1//A2B2.

同理，利用证法1或证法3中点的坐标，我们有和证法4类似的证法，过程略.

3.利用平面几何知识

解析几何是用代数方法研究几何问题，但解题时不能一味地单纯使用代数方法，应重视对平面几何知识的挖掘.

选修4-1《几何证明选讲》中有引理：如果一条直线截三角形的两边（或两边的延长线）所得的对应线段成比例，那么这条直线平行于三角形的第三边.

为了证“对应线段成比例”，结合选修4-4中的“点的极坐标与直角坐标的互化”的相关知识，我们可以把椭圆上的点的坐标设成极坐标的形式.

证法5：以原点为极点，x轴非负半轴为极轴，建立极坐标系.设曲线E1上异于原点任意一点P的极坐标为（ρ，

得曲线E1的极坐标方程

同理可得曲线E2的极坐标方程：ρ=

又A1，A2两点在直线l1上，可设A1（ρ1，α1），A2（ρ2，α1）. ρ1=|OA1|，ρ2=|OA2|.

则ρ1=

即ρ2=λρ1，

所以|OA2|=λ|OA1|.

同理可得|OB2|=λ|OB1|，则

同理，利用前三种证法中点的坐标，我们有和证法5类似的证法.下面以证法2中点的坐标为例.

证法6：由证法2知，A1（x1，y1），B1（x2，y2），A2（λx1，λy1），B2（λx2，λy2），

同理可得|OB2|=λ|OB1|，则

由于直线l1和l2过原点，证法2中点的坐标最简洁.张奠宙先生说：“我们知道‘点’是不能‘计算’的.但是引入

由平面几何知识易知A1B1∥A2B2，且了坐标，并把点看作位置向量，就可以计算了：向量可以和‘数’相乘，两个向量可以加减，以及有数量积等等……引入向量，能够精中求简，‘以简驭繁’……”

三、问题的启示

1.突出本质，注重核心，帮助学生提升核心素养

解析几何的本质是用代数方法研究图形的几何性质，而坐标法是解析几何中最基本的研究方法，其渗透了函数与方程、数形结合、分类讨论、化归与转化等重要思想.《普通高中数学课程标准（实验）》指出解析几何的核心内容包括几何图形的代数表示——点、直线、圆锥曲线的代数表示；常见几何图形、几何性质的代数表示；利用代数研究直线、圆锥曲线及直线与圆锥曲线的关系与性质.其教育价值在于通过坐标法下几何与代数统一性的认识，帮助学生建立普遍联系的辩证观念，发展学生的运算求解能力，拓展学生分析、解决问题的能力.因此，高中数学教学，必须贯彻课标理念，突出数学本质，关注学科各分支的核心内容，渗透重要的思想方法，并充分挖掘其教育价值，帮助学生提升核心素养.

2.立足教材，关注过程，重视探究，引领学生自主学习

高考源于教材，高于教材.教学中我们应当引导学生立足教材，研究教材：将教材呈现的知识形成知识网络、将教材中的特例推广为一般结论、将通法提升为思想方法，以期达到“八方联系，浑然一体”的境界.同时，高考作为选拔性考试，着力于学生学习潜能与学科核心素养的考查.教师要合理引导学生进行自主合作、交流探究活动，使学生亲身经历知识的发生与发展过程，体会蕴涵在其中的思想方法，领悟数学问题的本质，提高学生自主探究、知识综合运用能力，发展创新意识，从而引领学生自主学习.

1.周兴和.高等几何［M］.北京：科学出版社，2003.

2.波利亚.怎样解题［M］.涂鸿，冯承天，译.上海：上海科技教育出版社，2002.

3.唐秀颖.数学题解辞典（平面解析几何）［M］.上海：上海辞书出版社，1983.Z