巧用“1”解不等式

☉湖北省武汉二中 黄亦达

巧用“1”解不等式

☉湖北省武汉二中 黄亦达

不等式在数学研究和数学应用中起着重要作用，高中数学“课标”要求会用基本不等式解决简单的不等式问题，由于基本不等式既具有定性功能，又具有定理功能，还具有工具性的作用，应用面非常广泛，涉及高中数学各分支内容，因此在每年高考试卷中出现频率特高，可以说是每年高考的必考点.但是同学们利用基本不等式解题时，对部分题型已知条件中出现“1”情况如何进行代换，应用上还存在困惑.本文结合常见问题进行了分析和解答，希望能帮助同学们理解和掌握相关的知识.

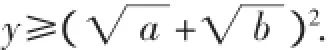
分析：为对（x+y）配式，根据1乘以任何一个式子大小不变，可将1整体代换，从而凑出定积的条件.

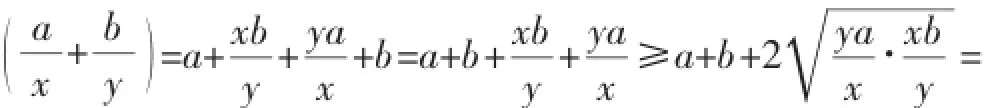
【针对练习】已知a＞0，b＞0，c＞0，且a+b+c=1.

分析：为对左式进行变换，可将各分式的分子中的1用a+b+c来代换.

证明：因为a＞0，b＞0，c＞0，且a+b+c=1，

根据不等式性质，得

分析：为了挖掘出定积的情况，根据“1乘以任何一个式子大小不变”，利用代换法，变换所求式子，可得到定积条件.

解答：因为a＞0，b＞0，且a+2b=1，

当且仅当a2=2b2，即当时，取最小值

例3已知a＞0，b＞0，c＞0，且abc=1.求证：（a+1）（b+1）（c+1）≥8.

分析：左边是3个因式的乘积，右边是数字，结合已知条件abc=1，如果能将左边转化为abc的乘积，根据“1的n次方仍是1”，问题就能解决.

由不等式的性质，得

因为abc=1，所以（a+1）（b+1）（c+1）≥8，

当且仅当a=b=c=1时等号成立.

针对练习：已知a＞0，b＞0，c＞0，且abc=1.证明

分析：左边是根式，右边是分式，结合已知条件，根式中每项除1，根式大小不变，再由基本不等式，去掉根号，转化为分式，问题就能解决.

证明：因为a＞0，b＞0，c＞0，且abc=1，

当且仅当a=b=c=1时等号成立.Z