复习回顾，深入挖掘，优化数学教学——“平面与平面平行的判定定理”一课引发的思考

☉江苏省梁丰高级中学 宋东娟

复习回顾，深入挖掘，优化数学教学
——“平面与平面平行的判定定理”一课引发的思考

☉江苏省梁丰高级中学 宋东娟

最近，观摩了上级教研部门组织的立体几何教学研讨活动，有两位教师开设了公开课，上课的主题是《平面与平面平行的判定定理》.众所周知，与传统的立体几何相比，新课程中立体几何教学发生了两大变化，一是从以往的点、线、面、体局部到整体展开转变为按照整体到局部的方式展开几何内容；二是从传统的对定理、性质的严格证明的思维过程转变为突出直观感知、操作确认、思辨论证、度量计算的探索历程.

本节课是在空间线线、线面、面面位置关系以及直线与平面平行的判定基础上展开的，两个平面平行的判定定理是立体几何中的一个重要定理，它揭示了线线平行、线面平行、面面平行的内在联系，体现了转化的数学思想.通过定理的探究，渗透“直观感知—操作确认—思辨论证”的认知方法，培养几何直观能力和抽象概括能力，为以后学习直线、平面垂直的判定及其性质打下基础.两位教师的教学设计与风格基本雷同，主要包含了以下几个过程.

一、一般的教学流程

（一）复习回顾，引入新课

问题1直线与平面有几种关系？线面平行如何定义？

问题2请分别用图形语言、文字语言、符号语言陈述直线与平面平行的判定定理.

问题3类比直线与平面平行的定义，你能描述一下平面与平面平行的定义吗？

问题4直接用定义判定面面平行方便吗？

（二）动手操作，探究新知

问题5一个三角板和或一本书，如何把三角板（书）所在平面都摆成与桌面平行的位置状态？

问题6调整三角板，使三角板的一条边所在的直线和桌面平行，这时三角板所在平面与桌面是否平行？

问题7调整三角板，使三角板的两条边所在的直线和桌面平行，这个三角板所在平面与桌面是否平行？

（三）借助模型，感知定理

问题8一个平面中一条直线与另一个平面平行，那么这两个平面平行吗？如果“一条直线”不够，那么“两条直线”、“三条直线”、“无数条直线”够了吗？

教师借助长方体模型，利用长方体中棱长所在直线与各面之间的关系与学生一起探究问题8，最后得到判定定理：如果一个平面内的两条相交直线与另一个平面平行，那么这两个平面平行.

图1

图2

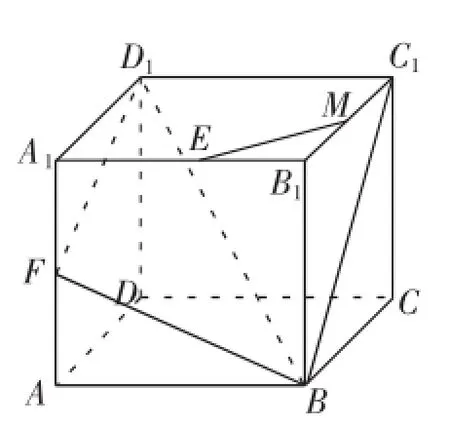
图3

（四）应用定理，内化规则

例1如图1，在正方体ABCD-A1B1C1D1中，求证：平面AB1D1∥平面C1BD.

变式1如图2，在正方体ABCD-A1B1C1D1中，P，Q，R分别为AA1，AB，AD中点.求证：平面PQR∥平面CB1D1.

变式2如图3，在正方体ABCD-A1B1C1D1中，点E，F，M分别是棱A1B1，AA1，B1C1的中点，在此正方体中，是否存在过点E，M且与平面BFD1平行的平面？若存在，请作出并证明；若不存在，请说明理由.

点评：本课的设计比较传统，一般教师都是按照这样的套路进行.以“直观感知—操作确认—思辨论证”的认识过程展开；精心设计问题，通过问题驱动的方式展开教学；以长（正）方体模型为载体，利用其

结构对称，各元素之间具有相等、平行、垂直等特点，直观研究线线、线面、面面位置关系；提供学生动手操作的机会，展开空间想象，主动建构知识.

二、存在的问题

虽然两节课从总体上讲循规蹈矩，不存在大的问题，但有两个教学细节还是让人觉得很困惑.

困惑1：两位教师都采用的是“复习回顾”的方式引入课题，通过复习线面平面的关系及判定定理，从而引发对面面平行的思考.这完全符合奥苏贝尔的“有意义学习”中的“先行组织者”理论.先行组织者是在课堂教学之前呈现的，通常是一个总的概述或类推，有助于学习者将学习材料置于一定背景中，从而构成“接受新材料的稳定中心”.“先行组织者”通常用于较为复杂的学习任务、较高级别的学习，是课堂教学前为学生提供的一个框架或结构，使得教学内容组织、转化成有意义关联的部分，无论是概念的学习，还是规律的发现，甚至问题的解决，高中数学学习的过程都可以称得上较为“复杂”的学习，因此，“先行组织者”对高中数学教学是非常必要的策略.［1］但两位教师的“复习回顾”似乎仅仅停留在“引入”的层面，没有进一步挖掘知识前后的联系，只是给人一种“例行公事”的感觉.

困惑2：两位教师基本上都是从一条、两条、无数条直线到两条相交直线的思路引导学生探究，寻找面面平行的判定条件（定理），这些探究是否符合数学知识的发生、发展过程？是否真正发展了学生的数学思维能力？很多老师的理由是在这之前学生经历过直线与平面的位置关系的研究过程，了解直线与平面平行转化为该直线与平面内一条直线的关系，所以，在寻找面面平行的判定条件时，首先考虑的是从一条直线开始，如果不够，再依次增加.上述理由看似合理，但前提是学生预先已经知道面面平行跟线面平行有关，否则只是教师的一厢情愿.

困惑3：两节课都是利用教材中的实例，比如三角尺、书本作为探索判定定理模型，而缺乏更生动、更实际的应用模型，这反映出教师在平时上课时拘泥于课本，将数学教学建立在教材的基础上，而很少联系实际生活，引导学生发现数学结论和建立数学概念.平面与平面平行的判定究竟对现实生活中有什么实际意义？

三、教学过程的优化

基于上述分析，本课的两个环节可以进行如下优化.

（一）引入环节

还是通过复习“线面平行的判定”引入，但不要仅仅局限于定理的本身，而是要深入挖掘定理获得过程所蕴含的数学思想.直线与平面平行的判定，主要是利用了转化的数学思想方法，即“高维”转为“低维”.在线面平行的判定中，把维度相对高的“线面平行”转化为维度相对低的“线线”平行来判定，这在立体几何的公理化体系中表现得淋漓尽致.比如，线与线的关系往往用“点”来刻画，判定线是否在面内，只需“两个点”在面内，面与面的关系往往用“线”来刻画，判断面与面是否相交，只需存在一条“公共直线”就行了.用“点”刻画线，用“线”刻画面，用“一维”来刻画“二维”，用“二维”刻画“三维”……用“低维”刻画“高维”这才是立体几何思想方法的精髓，我们常说的“空间问题平面化”就是充分体现了这个原理.因此，这个原理在复习引入中一定要展现给学生，并且要不断强化.如此，面面平行的判定思路自然清晰了，即要转化为“线面”平行，至于需要几次线面平行，那就是一些细枝末节的问题了.教学的大方向把握好，教学过程自然水到渠成.

通过复习回顾，不仅建立新、旧知识之间的联系，平面与平面的位置关系问题可以转化为直线与平面的位置关系问题，进而还可以转化为直线与直线的位置关系问题，而且为后续线面垂直的学习奠定了基础.

（二）应用环节

本课，虽然有三角板这一工具的助阵，但无法充分体现面面平行判定定理的应用价值.其实，立体几何的公理、定理都能再现实生活中找到生动的应用案例.比如，如何判定四条腿的凳子是否平稳，可先按紧其中三条凳腿，然后前后左右地晃，看另一条没被按紧的凳腿是否被“晃动”，如果纹丝不动，就说明凳子平稳了，这就是利用了立体几何的公理“不共线的三点确定一个平面”.面面平行的判定定理在现实中也有应用.木工师傅的水准器是比较常见的器械，这里面的依据就是面面平行的判定定理，教师事先准备一台，让学生动手操作、体验.

教师不是“教教材”，而是“用教材”.关注教材知识的前后联系，通过深入挖掘知识内涵，整合优化教材的知识结构，从而实现教材应用的“再创造”.

1.石志群.例谈“先行组织者”的途径与功能［J］.数学通报，2016（2）.Z