关注课本教学的几点思考

☉江苏省沭阳高级中学 纪秀艳

关注课本教学的几点思考

☉江苏省沭阳高级中学 纪秀艳

课本是考试内容的载体，是高考命题的参考依据.纵观近几年高考试卷，不难发现许多考题都可以在课本找到“影子”.但是，“轻视课本”大有人在，特别是在基础年段，由于数学概念的复杂性和抽象性，学生认为数学概念只要熟记即可，教师认为概念难以讲清楚，何况学生不感兴趣，照本宣科即可，这也就造成当前数学教学中不同程度地存在“概念知识一带而过”的局面，直接导致多数学生对数学概念的印象是模糊的，不利于高三的复习.为此，高三复习，教师要引导学生对一些重要数学概念进行回归再读.

一、关注课本知识的延伸性

课本例题和习题具有一定的示范性，我们不能简单地一解了之.下面以一道例题为例，谈谈如何进行深入的探究，对开发学生的智力、培养良好的思维品质的作用.

案例1用数学归纳法证明：（1+x）n≥1+nx（x＞-1，n为正整数）.（北师大版数学选修教材4-5数学归纳法一节例3）

本题作为选修教材中的内容，学生经过两年多的学习，其数学基础知识比较丰富，基本技能比较扎实，可以从多角度思考，尤其遇到与正整数有关的命题，除了数学归纳法之外，还可以函数、不等式、数列等多方面思考.本题题干中要求用数学归纳法证明本身就局限了学生的思维，将“用数学归纳法”这六个字删去，更能起到发展学生数学思维能力的作用.在教师的启发下，学生给出的几种证明方法：

证法1（数学归纳法）：（1）当n=1时，不等式明显成立.

（2）假设n=k时，命题成立，即（1+x）k≥1+kx，

那么当n=k+1时，因为x＞-1，x+1＞0，由假设（1+x）k≥1+ kx，得（1+x）k+1=（1+x）k（1+x）≥（1+kx）（1+x）=1+（k+1）x+kx2

因为kx2≥0，所以1+（k+1）x+kx2≥1+（k+1）x，

所以（1+x）k+1≥1+（k+1）x，

即n=k+1时命题成立.

综合（1）（2）知，命题成立

证法2（多元均值不等式）：当1+nx＜0时，原式显然成立，当1+nx＞0时，

证法3（运用数列解决问题）：不等式两端都含有自然数n，如果集中到一端可使问题简化.

an+1-an=

故an≤1恒成立，原命题得证.

证法4（导数法）：当n=1时，不等式显然成立.

当n≥2时，令f（x）=（1+x）n-nx-1，则f′（x）=n（1+x）n-1-n，显然，当x＞0时，f′（x）＞0，当-1＜x＜0时，f′（x）＜0，故f（x）在x=0处取得极小值，且f（0）=0，

故对于所有的x＞-1且x不为0，均有f（x）＞0，即（1+ x）n≥1+nx，原命题得证.

命题的推广：指数n如果不是正整数时，会有怎样的结论？

在中学数学教学中，例题教学占有相当重要的地位，研究例题不仅可以加深学生对概念、定理等基础知识的理解和掌握，更重要的是可以开发学生的智力，培养和提高学生解决问题的能力，从而促进学生数学素养的提高.因此，只有充分挖掘例题的内涵，拓展其外延，才能有效地促进学生的数学能力的提高.

二、关注课本知识体系

掌握概念就是掌握同类事物的共同本质属性.按照认识论原理，人类不可能一次地和孤立地认识一类事物的本质属性，必须用联系的方法，经历一个由感性到理性的发展过程.因此，回归课本概念，不是孤立、离散对待各个知识点，而应宏观看待各知识点之间的联系，“穿针引线”，建构知识体系.

在人教版必修4“向量”章节中指出：向量是既有大小又有方向的量，它既有代数和特征，又有几何特征，通过向量可以实现代数问题与几何问题的互相转化，所以向量是数形结合的桥梁.相比较而言，学生对向量的代数运算要容易接受一些，但对向量的几何运算往往感到比较困难，无从下手.因此，教学中可以结合课本知识，关注向量多方面的知识.

所以，从而△ABC是正三角形.

注：实质上本题中O为△ABC的外心和重心，证法1用代数法对学生要求比较高，关键是建系设出三点坐标；证法3利用三个等腰的三角形得出结论.

变形1：已知a+b+c=0，且|a|=3，|b|=5，|c|=7，求a与b的夹角θ.

分析：由已知得-c=a+b，两边同时平方得2a·b=15，于是cosθ=求△ABC的内角C的大小.

解法2：同解法法1求得，其

图1

解法1：可以仿上一题证法2，不难求出C=135°.

解法2：如图2所示，仿变形2很易求出∠AC′B=45°，再根据A，C，B，C′四点共圆，由此可求出结果.

注：解法2如果不借助图很易出错.

图2

解法1：以OA所在直线为x轴，过O垂直x轴的直线为y轴，建立直角坐标系，如图3所示，设∠AOC=α，扇形所对应的半径为r，则A（r，0），B.由很易得到方程组，再由辅助角公式不难求出的最大值为2.

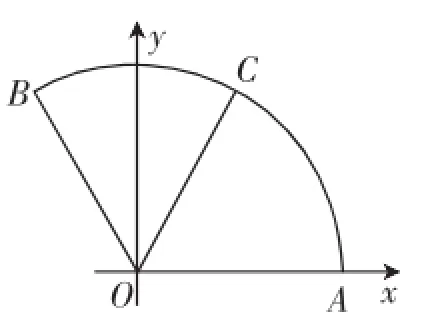
图3

解法3：仿解法1建立坐标系，如图4，过C分别作OA、OB的平行线，构造平行四边形ODCE，则x∠ODC=60°.在△ODC中，由余弦定理不难得到x2+y2-xy=1，这样就转化解法2.

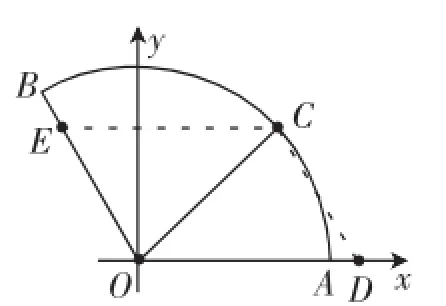
图4

向量的几何运算主要包括向量加减法的几何运算，在处理平面几何的有关问题时，往往有其独到之处，教师可让学有余力的学生课下继续探讨，以提高学生的思维发散能力.向量的代数运算关键是如何求出坐标，也就是要首先建系，选择适当坐标系对题目解决起着很大作用.本文的例题源于书本，这提示我们：要深入研究课本，拓展外延，才能真正地学以致用，达到能力的提升，适应高考，促进自身的发展.

事实上，“知识体系”是对课本概念再解读的重要手段，教师复习时要注意“授之以渔”，引导学生“实践反思”.当然，“建构知识体系”对高中学生而言，必要而又重要，教师关键在于引导.

三、关注课本知识的纵横迁移

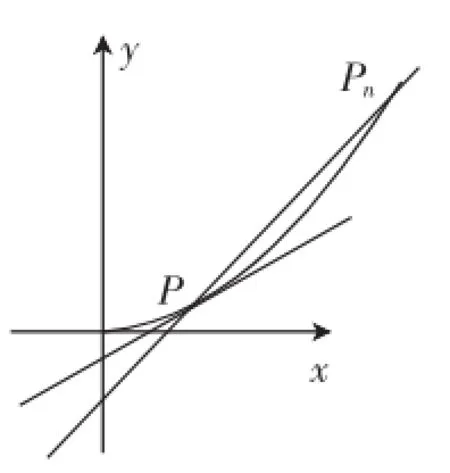
图5

明确概念，不仅要关注概念的内涵，同时要关注概念的外延，厘清概念与其他概念之间的关系，最终能较好实现知识之间的迁移.因此，回归课本概念，要对课本上的知识和方法加以总结提高，加以成“串”，使知识“升华”，最终达到知识间的“纵横迁移”.

比如，选修2-2中导数的几何意义——切线是一个重要的概念，在这概念中关键在于抓住“当Pn趋近于点P时，割线PPn趋近于切线”（如图5），即要关注“逼近思想”、“以直代曲”.

在这理解的基础上，不仅可以让学生明白“切线”定义的发展（切线不再是一般曲线（如圆锥曲线）中与曲线只有一个交点的直线，切线与曲线可以不止一个交点），关注曲线“在点P处的切线”与“过点P的切线”的差异；而且可以让学生更清晰地知道“已知函数的单调性，逆向求参数”时为什么要“等号”的原因（如y=x3在R上单调递增，但导数可能为0，如y′|x=0= 0）；进而让学生弄清楚“割线斜率”与“导数”之间的差异（后者是对前者的无限逼近，即取极限）.这样，当面对2012年福建省普通高中毕业班质量检查文科数学第12题：设函数f（x）及其导函数f′（x）都是定义在R上的函数，则“∀x1，x2∈R，且x1≠x2，|f（x1）-f（x2）|＜|x1-x2|”是“∀x∈R，|f′（x）|＜1”的（）.

A.充分而不必要条件B.必要而不充分条件

C.充要条件D.既不充分也不必要条件

我们的学生也许能较快辨认正确答案为B.

“纵横迁移”是对知识的一种“悟”，它离不开学习者对知识的理解掌握、拓展延伸、归纳反思，是回归再读课本概念的一个较高境界.复习时，教师关键在于引导学生用联系的眼光看待问题.比如可以“类比平面向量学习空间向量”，“可以用函数的眼光看待数列”等等，这样，数学的知识点不再孤立，知识间的纵横迁移也会水到渠成.

近几年的新课标卷越来越强调能力和方法的考查，能力和方法的提升离不开对数学概念的深刻理解，倘若复习时，我们能引导学生重视回归课本概念，关注概念形成，注重建构知识体系，努力实现纵横迁移，把课本的概念读懂、读透，这何尝不是一种人人可操作而又有效的复习手段！Z