基于CPFS理论的高三数学复习教学

☉江苏省启东中学 黄群力

基于CPFS理论的高三数学复习教学

☉江苏省启东中学 黄群力

一、CPFS理论

喻平教授在文1～文3中提出CPFS结构理论，其中CPFS结构是由下列四个概念组成的：概念域（concept field）指学习者在学习一个概念时头脑中形成了一组等价定义；概念系（concept system）指学习者在学习新概念时头脑中形成了一组概念及相互之间的关系；命题域（proposition field）指学习者在学习命题后头脑中形成了一组等价命题；命题系（proposition system）指学习者头脑中贮存了一组命题及相互之间存在推出关系.CPFS是取概念、命题、域、系四个英文单词的首字母组成的一种简单标记.CPFS结构理论对高三数学教学具有十分重要的指导意义.

二、CPFS理论与高三数学教学

1.高三数学复习过程是学生CPFS结构建立、优化的过程

目前高中各校数学教学的现状是，学生进入高三之前已学完整个高中阶段的数学知识.在高一、高二新课教学阶段，数学教学的重点是逐个击破知识点，知识点之间虽然有联系，但因为学生下位概念（命题）还没有学过，或是上位概念（命题）学生学过了但时间久远已经遗忘，加上进度的要求很难建立系统的知识之间的联系.而高三数学教学却没有上述知识与时间的限定，这一阶段的数学学习是全面复习高中数学内容，加强对各知识点及其联系的数学理解，初步形成个体的CPFS结构，“编织”知识网络，再利用形成的命题域、命题系指导解题，同时解题过程又使个体的CPFS结构不断得以补充、完善，其过程如图1所示.

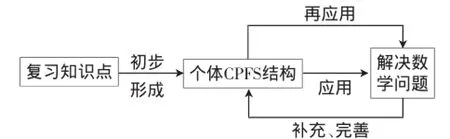
图1CPFS结构理论与高三数学复习数学

因此，基于CPFS结构理论，使得学生的认知结构不断完善，形成完备的知识网络，建立优良的CPFS结构是高三数学教学的主要任务.

2.优良的CPFS结构促进学生解题能力提高

高三数学教学大部分是解题教学.学生面临复杂问题时，一般需要先转化为几个较为简单的子问题，再逐一解决.而要实现问题的转化与划归，及时、有效地在命题域中提取出等价的形式，在命题系中选用合理的转化途径、调取适当的解决策略，必须具备稳固、完善的CPFS结构.例如，完备的等差（比）数列这一概念域（系）和命题域（系）结构对解决下面问题至关重要.

问题1已知数列｛an｝满足：a1=1，an+an+1=3·2n，n∈N*，求｛an｝的通项公式.

在解决该问题时，需要联想到下列相关的概念与命题：

A1：已知数列an+1、an之间的递推关系式和首项a1，则数列确定；

B1：若an+1-an=d（d为常数），则｛an｝为等差数列；

B2：若an+1÷an=q（q为非零常数），则｛an｝为等比数列；

C1：用累加法可求出等差数列的通项公式；

C2：用累乘法可求出等比数列的通项公式；

C3：数列｛an｝与其前n项和Sn之间满足关系an=

其中命题A1明确告诉我们该问题可求，命题Bi给我们提供了足够多的信息源泉，命题Ci激活了我们解决类似问题的方法，产生可靠类比依据，基于上述命题系，从不同角度出发可以找出问题的一些解决方法.

解法1：联想到由累加法推出等差数列的通项公式的过程，可得出下列解法：

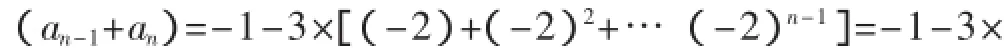
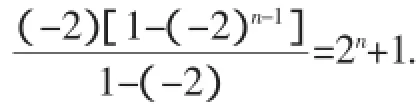
当n为奇数时，an=3·2n-1-an-1=2n-1，n≥3，n=1也适合.

综上得，an=2n+（-1）n-1，n∈N*.

解法2：联想到等比数列，可以用待定系数法构造一个等比数列，具体做法如下：

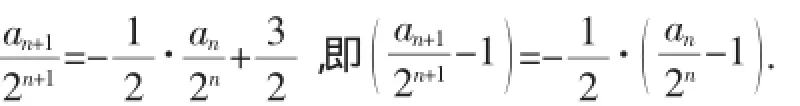
当n为偶数时，Sn=（a1+a2）+（a3+a4）+…+（an-1+an）=3×，即an=2n+（-1）n-1，

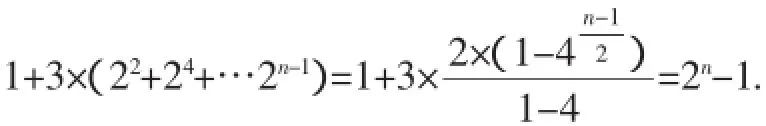
利用公式an=易得an=2n+（-1）n-1，n∈N*.

在“数列”这一大的命题系下，通过不同的联结方式得出问题1的三种解法，知识点之间的联结及思维过程如图2.在问题解决过程中，优良的CPFS结构起着关键的作用，因此，高三数学教学注重完善学生的CPFS结构，对学生解题能力的提高至关重要.

图2

三、高三数学教学促进学生优良的CPFS结构的教学策略

1.精心设置问题串，搭建命题之间的桥梁

CPFS结构建立仅凭课堂上简单地罗列知识框图是远远不够的，可靠、牢固的知识网络应该是在一个个数学问题的解答过程中形成.高三的学习时间紧、任务重，为了让学生在头脑中深深烙上知识之间的联络图，教师应将相关的概念和命题通过问题的形式精心设置成串，这样才能起到事半功倍的效果.例如，为了让学生理解等差与等比数列之间的联系，并进一步完善相关的概念域（系）结构，可设置下面的问题.

问题2对于给定数列｛cn｝，如果存在实常数p，q，使得cn+1=pcn+q（p≠0）对于任意的n∈N*都成立，我们称这个数列｛cn｝是“M类数列”.

（1）等差数列是否为“M类数列”，并举例说明；

（2）等比数列是否为“M类数列”，并举例说明；

（3）当p=2，q=1时，求｛cn｝的通项公式；

（4）当p=-1，q=2时，求｛cn｝的前n项和Sn，并判断｛Sn｝是否为“M类数列”；

（5）若数列｛an｝是“M类数列”，则数列｛an+an+1｝、｛an· an+1｝是否一定是“M类数列”.若是，加以证明；若不是，说明理由.

2.科学合理变式训练，凸现命题之间的联系

高三解题教学时，不能就题论题，问题解答后，教师应及时引导学生反思解题过程，再将原问题变式训练.变式分为等价和不等价两种形式，等价的变式问题可使学生在不同条件下关注到问题间的共同性，在辨别问题差异的过程中凸显问题本质，加深对等价概念或命题的理解，促使学生在头脑中建构某一概念的概念（命题）域；不等价的变式训练，通过相关概念（命题）的比较，让学生感受知识内在的联系和变通，学会根据不同情境选择适合的方法，通过知识间的变通和转化加强了学生头脑中概念（命题）之间的联系，促进该概念（命题）系的建构.

问题3直线l：x-y+c=0上存在点P，若过点P作圆O：x2+y2=4的两条切线PM，PN，且PM⊥PN，求c的取值范围.

变式1设A（1，0），B（-2，0），直线l：x-y+c=0上存在点P，使PB=2PA，求c的取值范围.

变式3设A（1，0），直线l：x-y+c=0上是否存在点B，使得圆O：x2+y2=4的任意点P都有PB=2PA成立，若存在，求出点B的坐标和此时c的值，若不存在，说明理由.

变式1将原问题中的“圆”等价变式成条件“PB= 2PA”，需要学生将该条件首先转化为“圆”后化归为原问题.变式2把“圆”改成“椭圆”，是不等价变式，难度加大，但保持了原问题中的本质特征及解决策略不变.变式3和前面几个问题的共同点是，需要先求出P点的轨迹方

程（用参数表示），但与前面几个问题比较，在处理“点存在”有明显不同.通过这种变与不变，增强学生对相关命题域和命题系的认识.

3.注重课堂交流探讨，促使学生在命题域（系）内发散思维

高三解题教学中学生经常听到抱怨，老师讲授的解法听得懂，但自己做的时候却想不到，特别是一些思维跨度比较大的解法.究其原因，还是学生头脑中的CPFS结构不稳固、不清晰，从而导致由此及彼的道路不畅通.如何有效地解决这一问题呢？因为每个学生的认知结构都有各自的不足，但同时也会对问题产生自己独特的理解，因此，课堂上教师应注重加强学生间的交流探讨，让学生充分发表自己的看法，在交流中认清知识之间的联系，探讨问题之间的转化方法，稳固头脑中的CPFS结构，同时也培养了学生的发散思维能力.

问题4已知实数a，b，c满足a+b+c=0，a2+b2+c2=3，求a的最大值.

不进则退，李高明在蒙自花了三万块，挨着一家生意红火的理发店，街头街尾地打起了“价格战”。此时的李高明，是小店五六个师傅中技术最好的，凡事他都想亲力亲为。有时生意好，给客人做头做到一两点，客人看晚了回不去，竟也乐意在他的小店里睡一宿。生意不好时，他犯愁，整夜整夜睡不着。心情起起伏伏地过了三个月，实在太煎熬，他受不了了。

师：由题目条件的特征，你能联想哪些学过的知识、方法？

生1：由a2+b2+c2=3想到圆的参数方程，所以可用三角换元法，具体解法如下：

由b2+c2=3-a2，可设b=，所以a=-（b+c）=所以，解得，故a的最大值为

生3：已知两个等式三个未知数，想到先代入消去未知数b，再利用根的判别式求解：

由a+b+c=0，得b=-a-c，代入a2+b2+c2=3，整理得2c2+ 2ac+2a2-3=0.因为c∈R，所以Δ=4a2-8（2a2-3）≥0，以下略.

生4：由已知的两个等式，相等利用不等式（x+y）2≤2（x2+y2）求解：

生5：由已知的一次、二次方程想到直线和圆的方程，用数形结合求解：

令b=x，c=y，则x+y=-a，x2+y2=3-a2，所以直线x+y=-a与圆x2+y2=3-a2有公共点，由d=，以下略.

课堂上学生大胆联想，交流探讨，从不等式、方程、函数、解析几何等不同角度出发，得到不同的解法，促进知识之间的联系.

4.注重学生自主探究，促进自主建构知识网络

探究数学问题的过程中，不仅需要掌握相关知识点，还要能够明晰知识点之间的逻辑关系.这一过程只有让学生独立自主去经历，才会对知识之间的联结理解更加深刻.有时候探究所花费时间可能比较长，但对个体的CPFS结构形成和完善却是经济高效的，同时不断完备的CPFS结构会促进解决问题的能力，有助于学生探究更多更难的问题.

探究的问题需要教师结合教学内容和学情精心设计，提出的问题应有助于学生的CPFS结构的建构，尽量避免随意性，例如在问题4教学完成后，可以让学生探究下面的问题.

问题5已知实数a，b，c满足a+b+c=1，a2+b2+c2=3，求abc的最大值.

（1）与问题4比较，问题5的条件和所求有哪些变化？

（2）这些变化对问题解决带来哪些困难？原来的方法还适用吗？

通过探究，让学生增强对解决问题4的几种知识点之间的联系理解，加深学生对命题之间关系的理解，建立命题之间稳固的联系.同时探究的问题加大了难度，解决时需要更多的知识，从而在已形成的CPFS结构上添加了新的元素和联结，使得学生的认知结构得以更新和升级.

1.喻平.数学学习心理的CPFS结构理论［M］.南宁：广西教育出版社，2008.

2.喻平.数学问题解决中个体的CPFS结构对迁移影响的研究［J］.数学教育学报，2004（1）.

3.喻平，李渺，杨义莹.个体CPFS结构与探究问题能力的关系研究［J］.数学教育学报，2006（3）.

4.金山.一道解析几何问题的探究教学设计与实践［J］.中小学数学，2015（9）.F